2.3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΔΙΑΣΠΟΡΑΣ Εισαγωγή Εκτός από τους στατιστικούς πίνακες και τα διαγράμματα υπάρχουν και αριθμητικά μέτρα με τα οποία μπορούμε να περιγράψουμε με συντομία μια κατανομή συχνοτήτων. Η γνώση των μέτρων αυτών διευκολύνει και την παραπέρα στατιστική επεξεργασία των δεδομένων. Έστω, για παράδειγμα, ένας καθηγητής ο οποίος, για να συγκρίνει δύο διαφορετικά τμήματα Α και Β της ίδιας τάξης ως προς την επίδοσή τους σε ένα μάθημα, πήρε τυχαία 10 μαθητές από κάθε τμήμα. Η βαθμολογία τους στο μάθημα αυτό ήταν: Τμήμα Α: 13 13 14 15 15 15 15 16 16 18
Παρατηρούμε ότι η βαθμολογία και των δύο τμημάτων είναι συγκεντρωμένη γύρω στο 15, αλλά το δεύτερο τμήμα παρουσιάζει μεγαλύτερη διασπορά βαθμών από το πρώτο. Δηλαδή, οι βαθμοί του Β΄ τμήματος είναι περισσότερο διασκορπισμένοι γύρω από μια “κεντρική” τιμή. Οι έννοιες “κεντρική τιμή” και “διασπορά των παρατηρήσεων” μας δίνουν το ερέθισμα για έναν ακόμα πιο σύντομο τρόπο περιγραφής της κατανομής ενός συνόλου δεδομένων. Για να ορίσουμε δηλαδή κάποια μέτρα (αριθμητικά μεγέθη), που να μας δίνουν α) τη θέση του “κέντρου” των παρατηρήσεων στον οριζόντιο άξονα και β) τη διασπορά των παρατηρήσεων, δηλαδή πόσο αυτές εκτείνονται γύρω από το “κέντρο” τους. Τα πρώτα τα καλούμε μέτρα θέσης της κατανομής (location measures), ενώ τα δεύτερα μέτρα διασποράς ή μέτρα μεταβλητότητας (measures of variability). Εκτός από τα μέτρα θέσης και διασποράς μιας κατανομής πολλές φορές είναι απαραίτητος και ο προσδιορισμός κάποιων άλλων μέτρων, που καθορίζουν τη μορφή της κατανομής. Κατά πόσο δηλαδή η αντίστοιχη καμπύλη συχνοτήτων είναι συμμετρική ή όχι ως προς την ευθεία x = x0, για δεδομένο σημείο x0 του άξονα 0x. Τα μέτρα αυτά, που συνήθως εκφράζονται σε συνάρτηση με τα μέτρα θέσης και διασποράς, καλούνται μέτρα ασυμμετρίας (measures of skewness). |
Υπολογίζοντας από ένα σύνολο δεδομένων κάποια από τα ανωτέρω μέτρα, μπορούμε να έχουμε μια σύντομη περιγραφή της μορφής της καμπύλης συχνοτήτων. Στο σχήμα 12 οι καμπύλες συχνοτήτων Α και Β είναι συμμετρικές με το ίδιο “κέντρο” x0, αλλά η Β έχει μεγαλύτερη μεταβλητότητα από την Α. Οι καμπύλες Γ και Δ είναι ασύμμετρες, με τη Γ όπως λέμε να παρουσιάζει θετική ασυμμετρία και τη Δ αρνητική ασυμμετρία. Το “κέντρο” της Γ είναι αριστερότερα του x0, ενώ της Δ είναι δεξιότερα του x0. Η Δ παρουσιάζει μεγαλύτερη μεταβλητότητα από τη Γ. Μέτρα Θέσης Τα πιο συνηθισμένα μέτρα που χρησιμοποιούνται για την περιγραφή της θέσης ενός συνόλου δεδομένων πάνω στον οριζόντιο άξονα ox, εκφράζοντας την “κατά μέσο όρο” απόστασή τους από την αρχή των αξόνων, είναι ο αριθμητικός μέσος ή μέση τιμή (arithmetic mean or average), η διάμεσος (median) και η κορυφή ή επικρατούσα τιμή (mode). α) Μέση Τιμή Η μέση τιμή ενός συνόλου ν παρατηρήσεων αποτελεί το σπουδαιότερο και χρησιμότερο μέτρο της Στατιστικής και ορίζεται ως το άθροισμα των παρατηρήσεων διά του πλήθους των παρατηρήσεων.
όπου το σύμβολο
Η παραπάνω σχέση ισοδύναμα γράφεται:
όπου fi οι σχετικές συχνότητες. Για παράδειγμα, η μέση επίδοση των μαθητών στο τμήμα Α θα είναι σύμφωνα με την (1)
ή ισοδύναμα από τον αντίστοιχο πίνακα συχνοτήτων σύμφωνα με την (2). |
Ομοίως, υπολογίζεται και η μέση επίδοση για το τμήμα Β, η οποία είναι πάλι
Επίσης, το μέσο ύψος των 40 μαθητών της Γ΄ Λυκείου του πίνακα 8, σύμφωνα με τη σχέση (1) είναι Για ευκολότερο όμως υπολογισμό χρησιμοποιούμε τον πίνακα συχνοτήτων, όπως αυτός δίνεται παρακάτω, ομαδοποιώντας τα δεδομένα σε κ = 6 κλάσεις. Αν xi είναι το κέντρο της i κλάσης και νi η αντίστοιχη συχνότητα, τότε σύμφωνα με τη σχέση (2) η μέση τιμή θα είναι:
Παρατηρούμε ότι οι δύο μέσες τιμές του ίδιου συνόλου δεδομένων δεν είναι ακριβώς οι ίδιες. Πού οφείλεται αυτή η, έστω και μικρή, διαφορά;
Η διαφορά αυτή οφείλεται στο γεγονός ότι κατά την ομαδοποίηση υποθέσαμε ότι οι παρατηρήσεις κάθε κλάσης είναι ομοιόμορφα κατανεμημένες και ότι οι τιμές της μεταβλητής σε κάθε κλάση εκπροσωπούνται από την αντίστοιχη κεντρική τιμή xi. Η υπόθεση αυτή σημαίνει απώλεια πληροφοριών για τις αρχικές τιμές. Χάνουμε λοιπόν λίγο ως προς στην ακρίβεια κερδίζουμε όμως χρόνο! β) Σταθμικός Μέσος Στις περιπτώσεις που δίνεται διαφορετική βαρύτητα (έμφαση) στις τιμές x1, x2 ,..., xν ενός συνόλου δεδομένων, τότε αντί του αριθμητικού μέσου χρησιμοποιούμε τον σταθμισμένο αριθμητικό μέσο ή σταθμικό μέσο (weighted mean). |
| Εάν σε κάθε τιμή x1, x2,..., xν δώσουμε διαφορετική βαρύτητα, που εκφράζεται με τους λεγόμενους συντελεστές στάθμισης (βαρύτητας) w1, w2,..., wν, τότε ο σταθμικός μέσος βρίσκεται από τον τύπο:
Για παράδειγμα, με το νέο σύστημα, για την εισαγωγή ενός μαθητή στην τριτοβάθμια εκπαίδευση θα συνυπολογίζονται ο βαθμός x1 του απολυτηρίου του Ενιαίου Λυκείου με συντελεστή (βάρος) w1 = 7 ,5, ο βαθμός x2 στο τεστ δεξιοτήτων με συντελεστή w2 = 1, ο βαθμός x3 στο 1ο βασικό μάθημα με συντελεστή w3 = 1 και ο βαθμός x4 στο 2ο βασικό μάθημα με συντελεστή w4 = 0,5. Εάν ένας μαθητής πάρει τους βαθμούς x1 = 16,5, x2 = 18, x3 = 17 και x4 = 16,6, τότε ο σταθμικός μέσος της επίδοσης του θα είναι:
γ) Διάμεσος (δ) Οι χρόνοι (σε λεπτά) που χρειάστηκαν 9 μαθητές, για να λύσουν ένα πρόβλημα είναι: 3, 5, 5, 36, 6, 7, 4, 7, 8 με μέση τιμή Διάμεσος (δ) ενός δείγματος ν παρατηρήσεων οι οποίες έχουν διαταχθεί σε αύξουσα σειρά ορίζεται ως η μεσαία παρατήρηση, όταν το ν είναι περιττός αριθμός, ή ο μέσος όρος (ημιάθροισμα) των δύο μεσαίων παρατηρήσεων όταν το ν είναι άρτιος αριθμός. Για παράδειγμα, για να βρούμε τη διάμεσο των δεδομένων: |
| α) Έχουμε ν = 13 παρατηρήσεις, οι οποίες σε αύξουσα σειρά είναι: 0 1 1 1 2 3 4 5 6 6 8 8 9. Άρα, η διάμεσος είναι η μεσαία παρατήρηση (έβδομη στη σειρά), δ = 4. β) Έχουμε ν = 14 παρατηρήσεις οι οποίες σε αύξουσα σειρά είναι:0 1 1 1 2 3 4 5 6 6 8 8 9 9. Άρα, η διάμεσος είναι το ημιάθροισμα των δύο μεσαίων παρατηρήσεων (της έβδομης και όγδοης στη σειρά), δηλαδή Παρατηρούμε ότι, η διάμεσος είναι η τιμή που χωρίζει ένα σύνολο παρατηρήσεων σε δύο ίσα μέρη όταν οι παρατηρήσεις αυτές τοποθετηθούν με σειρά τάξης μεγέθους. Ακριβέστερα, η διάμεσος είναι η τιμή για την οποία το πολύ 50% των παρατηρήσεων είναι μικρότερες από αυτήν και το πολύ 50% των παρατηρήσεων είναι μεγαλύτερες από την τιμή αυτήν. Διάμεσος σε Ομαδοποιημένα Δεδομένα Θεωρούμε τα δεδομένα του ύψους των μαθητών στον πίνακα 9 και το αντίστοιχο ιστόγραμμα αθροιστικών σχετικών συχνοτήτων με την πολυγωνική γραμμή, σχήμα 13. Η διάμεσος, όπως ορίστηκε, αντιστοιχεί στην τιμή x = δ της μεταβλητής Χ (στον οριζόντιο άξονα), έτσι ώστε το 50% των παρατηρήσεων να είναι μικρότερες ή ίσες του δ. Δηλαδή, η διάμεσος θα έχει αθροιστική σχετική συχνότητα Fi = 50% . Εφόσον στον κάθετο άξονα έχουμετις αθροιστικές σχετικές συχνότητες, από το σημείο Α (50% των παρατηρήσεων) φέρουμε την
|
| δ) Εκατοστημόρια (Pκ) Όπως ορίσαμε τη διάμεσο δ, έτσι ώστε το πολύ 50% των παρατηρήσεων να είναι μικρότερες του δ και το πολύ 50% των παρατηρήσεων να είναι μεγαλύτερες του δ, μπορούμε ανάλογα να ορίσουμε και τα εκατοστημόρια (percentiles) Pκ, κ = 1,2,...,99 . Οι τιμές P1, P2,..., P99 χωρίζουν τη συνολική συχνότητα σε 100 ίσα μέρη. Επομένως, αναλόγως και με τον ορισμό της διαμέσου, ορίζουμε ως κ-εκατοστιαίο σημείο ή Pκ εκατοστημόριο ενός συνόλου παρατηρήσεων την τιμή εκείνη για την οποία το πολύ κ% των παρατηρήσεων είναι μικρότερες του Pκ και το πολύ (100-κ)% των παρατηρήσεων είναι μεγαλύτερες από την τιμή αυτήν.
|
| Εκατοστημόρια σε Ομαδοποιημένα Δεδομένα Ο υπολογισμός των εκατοστημορίων (ή τεταρτημορίων) σε ομαδοποιημένα δεδομένα γίνεται όπως και στη διάμεσο από το πολύγωνο αθροιστικών σχετικών συχνοτήτων. Στο σχήμα 13 δίνονται τα Q1, Q2 = δ, Q3 και P10, P90 για τα δεδομένα του πίνακα 9, από το οποίο βρίσκουμε κατά προσέγγιση: P10 = 162,5, Q1 = 168, δ =173, Q3 = 178 και P90 = 184. ε) Επικρατούσα Τιμή (M0) Στην περίπτωση μη ομαδοποιημένων δεδομένων επικρατούσα τιμή ή κορυφή (mode) M0 ορίζεται ως η παρατήρηση με τη μεγαλύτερη συχνότητα. Είναι προφανές ότι η επικρατούσα τιμή μπορεί να οριστεί και στην περίπτωση ποιοτικών δεδομένων, ενώ τα άλλα μέτρα που είδαμε ορίζονται μόνο για ποσοτικά δεδομένα. Για παράδειγμα:
γ) Για να βρούμε την επικρατούσα τιμή των παρατηρήσεων 0 1 1 2 2 2 3 4 4 4 5 5 7 8, κατασκευάζουμε το διπλανό πίνακα συχνοτήτων. Οι τιμές 2 και 4 είναι και οι δύο επικρατούσες τιμές, γιατί καθεμιά έχει συχνότητα 3. Βλέπουμε εδώ ότι η επικρατούσα τιμή μπορεί να μην είναι μοναδική. Όταν έχουμε δύο κορυφές, η αντίστοιχη κατανομή συχνοτήτων λέγεται δικόρυφη (bimodal), ενώ όταν έχουμε πολλές κορυφές λέγεται πολυκόρυφη (multimodal). |
| Επικρατούσα Τιμή σε Ομαδοποιημένα Δεδομένα Όταν έχουμε ομαδοποιημένα (ποσοτικά) δεδομένα σε ισοπλατείς κλάσεις, τότε βρίσκουμε πρώτα την επικρατούσα κλάση i, δηλαδή την κλάση με τη μεγαλύτερη συχνότητα. 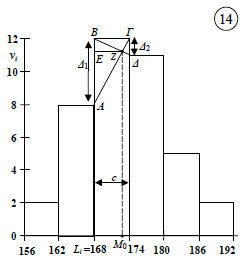 Υποθέτοντας, όπως έχουμε ήδη αναφέρει και προηγουμένως, ότι οι παρατηρήσεις στις κλάσεις κατανέμονται ομοιόμορφα, η επικρατούσα τιμή προσδιορίζεται, όπως φαίνεται στο διπλανό σχήμα 14, ως η τετμημένη του σημείου τομής Ζ των ευθύγραμμων τμημάτων ΑΓ και ΒΔ. Στο σχήμα αυτό δίνεται η κορυφή για το ύψος των μαθητών του πίνακα 9. Κατά προσέγγιση η κορυφή (επικρατέστερο ύψος) είναι M0 ≈173 cm. Μέτρα Διασποράς Στα προηγούμενα είδαμε ότι τα μέτρα θέσης παρέχουν κάποια πληροφορία για την κατανομή ενός πληθυσμού. Αυτά όμως δεν επαρκούν, για να περιγράψουν πλήρως την κατανομή, όπως διαπιστώσαμε στην αρχή της § 2.3 συγκρίνοντας τις βαθμολογίες των μαθητών δύο τμημάτων Α και Β στα σχήματα 11(α), (β). Ενώ οι βαθμολογίες των δύο τμημάτων Α και Β έχουν ίσες μέσες τιμές |
| α) Εύρος (R) Το απλούστερο από τα μέτρα διασποράς είναι το εύρος ή κύμανση (range) (R), που ορίζεται ως η διαφορά της ελάχιστης παρατήρησης από τη μέγιστη παρατήρηση, δηλαδή: Εύρος R = Μεγαλύτερη παρατήρηση-Μικρότερη παρατήρηση Έτσι, για τη βαθμολογία του τμήματος Α το εύρος είναι RA = 18 - 13 = 5, ενώ για το τμήμα Β, RB = 20 - 10 = 10, τιμές που επιβεβαιώνουν ότι πράγματι στο τμήμα Β έχουμε μεγαλύτερη διασπορά βαθμολογίαςπαρά στο τμήμα Α. β) Ενδοτεταρτημοριακό Εύρος (Q) Το ενδοτεταρτημοριακό εύρος (interquartile range) είναι η διαφορά του πρώτου τεταρτημορίου Q1 από το τρίτο τεταρτημόριο Q3, δηλαδή: Q = Q3 - Q1 Στο μεταξύ τους διάστημα περιλαμβάνεται το 50% των παρατηρήσεων. Επομένως όσο μικρότερο είναι αυτό το διάστημα, τόσο μεγαλύτερη θα είναι η συγκέντρωση των τιμών και άρα μικρότερη η διασπορά των τιμών της μεταβλητής. |
| γ) Διακύμανση (s2) Ένας άλλος τρόπος για να υπολογίσουμε τη διασπορά των παρατηρήσεων t1,t2,...,tv μιας μεταβλητής Χ θα ήταν να αφαιρέσουμε τη μέση τιμή
Ο αριθμός όμως αυτός είναι ίσος με μηδέν, αφού
Γι’αυτό, ως ένα μέτρο διασποράς παίρνουμε τον μέσο όρο των τετραγώνων των αποκλίσεων των t1 από τη μέση τιμή τους
Ο τύπος αυτός αποδεικνύεται ότι μπορεί να πάρει την ισοδύναμη μορφή:
η οποία διευκολύνει σημαντικά τους υπολογισμούς κυρίως όταν η μέση τιμή
ή την ισοδύναμη μορφή: |
|
όπου x1, x2 ,...,xκ οι τιμές της μεταβλητής (ή τα κέντρα των κλάσεων) με αντίστοιχες συχνότητες ν1, ν2,..., νκ.
ενώ για τους μαθητές του τμήματος Β βρίσκουμε
Επομένως:
Εάν υπολογίσουμε τη διακύμανση από τα μη ομαδοποιημένα δεδομένα του πίνακα 8, βρίσκουμε s2 = 50,9. Η διαφορά αυτή οφείλεται στην απώλεια πληροφορίας λόγω ομαδοποίησης των παρατηρήσεων. | ||||||||||||||||||
| δ) Τυπική Απόκλιση (s) Η διακύμανση είναι μια αξιόπιστη παράμετρος διασποράς, αλλά έχει ένα μειονέκτημα. Δεν εκφράζεται με τις μονάδες με τις οποίες εκφράζονται οι παρατηρήσεις. Για παράδειγμα, αν οι παρατηρήσεις εκφράζονται σε cm, η διακύμανση εκφράζεται σε cm2. Αν όμως πάρουμε τη θετική τετραγωνική ρίζα της διακύμανσης, θα έχουμε ένα μέτρο διασποράς που θα εκφράζεται με την ίδια μονάδα μέτρησης του χαρακτηριστικού, όπως ακριβώς είναι και όλα τα άλλα μέτρα θέσης, που εξετάσαμε έως τώρα. Η ποσότητα αυτή λέγεται τυπική απόκλιση (standard deviation), συμβολίζεται με s και δίνεται από τη σχέση:
Η τυπική απόκλιση για το ύψος των μαθητών του πίνακα 4 είναι από το προηγούμενο παράδειγμα s = √53,4 = 7,3 cm αν αυτή υπολογιστεί από τα ομαδοποιημένα δεδομένα του πίνακα 9, ή s = √50,9 = 7,13 cm, αν υπολογιστεί από τα μη ομαδοποιημένα δεδομένα του πίνακα 8. 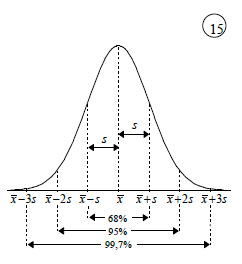 i) το 68% περίπου των παρατηρήσεων βρίσκεται στο διάστημα
ii) το 95% περίπου των παρατηρήσεων βρίσκεται στο διάστημα
iii) το 99,7% περίπου των παρατηρήσεων βρίσκεται στο διάστημα
iv) το εύρος ισούται περίπου με έξι τυπικές αποκλίσεις, δηλαδή R ≈ 6s. |
| Συντελεστής Mεταβολής (CV) Έστω ότι από ένα δείγμα είκοσι μαθητών της Α΄ Γυμνασίου βρήκαμε μέσο βάρος
Ο συντελεστής μεταβολής εκφράζεται επί τοις εκατό, είναι συνεπώς ανεξάρτητος από τις μονάδες μέτρησης και παριστάνει ένα μέτρο σχετικής διασποράς των τιμών και όχι της απόλυτης διασποράς, όπως έχουμε δει έως τώρα. Εκφράζει, δηλαδή, τη μεταβλητότητα των δεδομένων απαλλαγμένη από την επίδραση της μέσης τιμής. Για το πρώτο παράδειγμα του βάρους έχουμε συντελεστή μεταβολής για τις δύο ομάδες μαθητών:
δηλαδή, ο βαθμός διασποράς του βάρους των μαθητών Γυμνασίου είναι μεγαλύτερος από το βαθμό διασποράς του βάρους των μαθητών Λυκείου (για τα συγκεκριμένα δείγματα). |
ΕΦΑΡΜΟΓΕΣ
1. Ο διπλανός πίνακας συχνοτήτων δίνει την κατανομή του χρόνου Χ (σε sec) 60 μαθητών β) η τυπική απόκλιση, γ) σε πόσο χρόνο από της στιγμή της εκκίνησης κάλυψε την απόσταση το 25% των μαθητών.
ΛΥΣΗ α)
Επομένως, ο μέσος χρόνος για την κάλυψη της συγκεκριμένης απόστασης είναι:
β) Για τον υπολογισμό της τυπικής απόκλισης είναι προτιμότερο να εφαρμόσουμε τη σχέση (4), μιας και η μέση τιμή δεν είναι ακέραιος αριθμός. Με βάση τον παραπάνω πίνακα η διακύμανση της μεταβλητής Χ είναι:
και η τυπική απόκλιση s = √70,56 = 8,4 sec. γ) Θέλουμε να υπολογίσουμε το πρώτο τεταρτημόριο, Q1. Αριστερά της διαμέσου δ = 67,5 έχουμε 30 παρατηρήσεις. Η διάμεσος αυτών των 30 πρώτων παρατηρήσεων είναι το ημιάθροισμα της 15ης και 16ης παρατήρησης, δηλαδή Q1 = (60 + 60) / 2 = 60 sec. Δηλαδή, ύστερα από μία ώρα από τη στιγμή της εκκίνησης το 25% των μαθητών κάλυψαν τη συγκεκριμένη απόσταση. 2. Να αποδειχτεί ότι η συνάρτηση
γίνεται ελάχιστη, όταν ΛΥΣΗ Λαμβάνοντας την πρώτη παράγωγο της f(λ), βρίσκουμε f'(λ) = -2(x1 - λ) - 2(x2 - λ)... - 2(xν - λ). Έχουμε διαδοχικά:
Η δεύτερη παράγωγος της της f(λ) είναι:
και επειδή |
| 3. Έστω x1, x2 ,..., xv ν παρατηρήσεις με μέση τιμή  β) Αν y1, y2,..., yv είναι οι παρατηρήσεις που προκύπτουν αν πολλαπλασιάσουμε σε καθεμιά από τις x1, x2,..., xv μια σταθερά c, να αποδειχτεί ότι: 
ΑΠΟΔΕΙΞΗ α) Έχουμε yi = xi + c, i = 1,2,...,v, επομένως: i) 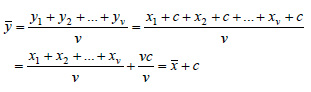 ii) 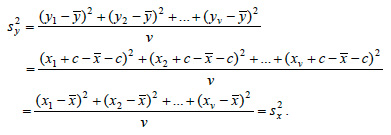 Άρα και sy = sx. β) Έχουμε yi = cxi, i = 1,2,...,v, επομένως: i) 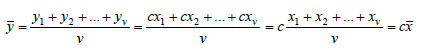 ii) 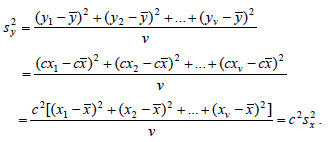 Άρα και sy = |c|sx. |
Ασκήσεις
| ||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||