2.4 ΓΡΑΜΜΙΚΗ ΠΑΛΙΝΔΡΟΜΗΣΗ

Εισαγωγή

Στα διάφορα προβλήματα που εξετάσαμε έως τώρα στη Στατιστική ασχοληθήκαμε κάθε φορά με μία μόνο μεταβλητή (ξεχωριστά), π.χ. με το βάρος, με το ύψος, με την επίδοση μαθητών κτλ. Για καθεμιά μεμονωμένη μεταβλητή αρκεστήκαμε στη μελέτη της κατανομής συχνοτήτων, στον υπολογισμό διάφορων μέτρων όπως μέση τιμή, διάμεσος, διακύμανση κτλ. Σε αρκετές όμως περιπτώσεις εξίσου ενδιαφέρουσα είναι και η ταυτόχρονη μελέτη δύο ή περισσότερων μεταβλητών, για να προσδιορίσουμε με ποιο τρόπο οι μεταβλητές αυτές σχετίζονται μεταξύ τους. Για παράδειγμα:
α) Η ηλικία και το βάρος ενός παιδιού έχουν κάποια θετική εξάρτηση (συσχέτιση) μεταξύ τους με την έννοια ότι όσο πιο μεγάλο είναι το παιδί τόσο μεγαλύτερο βάρος θα έχει.
β) Η διάρκεια ζωής των ζώντων οργανισμών σε μια περιοχή και το ποσοστό μόλυνσης της περιοχής έχουν αρνητική εξάρτηση μεταξύ τους, με την έννοια ότι όσο πιο μεγάλο είναι το ποσοστό μόλυνσης της περιοχής τόσο μικρότερη είναι η διάρκεια ζωής των οργανισμών που ζουν στην περιοχή.
γ) Όσο μεγαλύτερη (μέχρι ένα ανώτερο όριο) είναι η περιεκτικότητα σε φθόριο στο πόσιμο νερό, τόσο μικρότερες είναι οι περιπτώσεις στη φθορά των δοντιών των μικρών παιδιών.
δ) Η συνολική παραγωγή καλαμποκιού εξαρτάται από τη θέση του χωραφιού, από την ποσότητα λιπάσματος, από την επίδραση της θερμοκρασίας, της υγρασίας κτλ.
ε) Το ύψος των αποδοχών των υπαλλήλων μιας εταιρείας δεν εξαρτάται από το βάρος τους.
Έτσι λοιπόν είναι ενδιαφέρον να εξεταστούν οι επιδράσεις που κάποιες μεταβλητές ασκούν σε κάποιες άλλες μεταβλητές. Η ύπαρξη μιας συναρτησιακής σχέσης (εξίσωσης) μεταξύ των μεταβλητών μπορεί να είναι εξαιρετικά πολύτιμη για την πρόβλεψη των τιμών μιας μεταβλητής από τις γνώσεις που διαθέτουμε για τις άλλες μεταβλητές, όταν ισχύουν κάποιες συγκεκριμένες συνθήκες.
Ο κλάδος της Στατιστικής που εξετάζει τη σχέση μεταξύ δύο ή περισσότερων μεταβλητών με απώτερο σκοπό την πρόβλεψη μιας απ’αυτές μέσω των άλλων χαρακτηρίζεται με την ονομασία ανάλυση παλινδρόμησης (regression analysis). Ιστορικά, ο όρος “regression” χρησιμοποιήθηκε για πρώτη φορά από τον Άγγλο ανθρωπολόγο Galton (1822-1911) το 1885. Με τη μελέτη του ύψους των παιδιών σε σχέση με το ύψος των γονέων διαπιστώθηκε ότι παιδιά ψηλών γονέων τείνουν, κατά μέσο όρο, να είναι κοντύτερα των γονιών τους, ενώ παιδιά κοντών γονέων τείνουν, κατά μέσο όρο, να γίνονται ψηλότερα των γονιών τους.

Απλή Γραμμική Παλινδρόμηση

Η απλούστερη περίπτωση παλινδρόμησης είναι η απλή γραμμική παλινδρόμηση (simple linear regression), κατά την οποία υπάρχει μόνο μια ανεξάρτητη μεταβλητή X (independent or input variable), και η εξαρτημένη μεταβλητή Y (dependent or response variable), η οποία μπορεί να προσεγγιστεί ικανοποιητικά από μία γραμμική συνάρτηση του X. Η περίπτωση αυτή εμφανίζεται τόσο σε πειραματικές όσο και σε μη πειραματικές μελέτες. Στις πειραματικές μελέτες ο ερευνητής καθορίζει, για παράδειγμα, από πριν τις δόσεις ενός φαρμάκου (ανεξάρτητη μεταβλητή) που δίνει στα πειραματόζωα και μετρά τις αντιδράσεις τους (εξαρτημένη μεταβλητή). Με την παλινδρόμηση ενδιαφέρεται να προσδιορίσει μία σχέση δόσης-αντίδρασης για το συγκεκριμένο φάρμακο. Στις μη πειραματικές μελέτες ή δειγματοληψίες, γίνονται μετρήσεις σε δύο χαρακτηριστικά (μεταβλητές) για κάθε άτομο (μονάδα) του δείγματος. Σε ένα δείγμα 10 μαθητών μετράμε, για παράδειγμα, το βάρος και το ύψος τους. Η διάκριση εδώ μεταξύ ανεξάρτητης και εξαρτημένης μεταβλητής είναι δύσκολη. Αν αυτό που μας ενδιαφέρει είναι το “τι συμβαίνει με το βάρος των παιδιών όταν αλλάζει το ύψος τους”, τότε θεωρούμε ως ανεξάρτητη μεταβλητή X το ύψος και ως εξαρτημένη μεταβλητή Y το βάρος. Οπότε, ενδιαφερόμαστε για την παλινδρόμηση του βάρους (Y) πάνω στο ύψος (X). Αντίθετα, αν μας ενδιαφέρει το “τι συμβαίνει με το ύψος των παιδιών όταν αλλάζει το βάρος τους”, τότε θεωρούμε ως ανεξάρτητη μεταβλητή Χ το βάρος και ως εξαρτημένη μεταβλητή Υ το ύψος. Τότε έχουμε παλινδρόμηση του ύψους (Υ) πάνω στο βάρος (Χ).

Διάγραμμα Διασποράς

Ο παρακάτω πίνακας 10 δίνει τα ύψη X (σε cm) και τα βάρη Y (σε kg) των 18 αγοριών της Γ΄ Λυκείου του πίνακα 4. Οι τιμές του ύψους δίνονται σε αύξουσα σειρά.

Πίνακας 10

Λίστα υψών (σε cm) και βαρών (σε kg) των 18 αγοριών του πίνακα 4.

Στο παράδειγμα αυτό έχουμε την περίπτωση όπου σε κάθε άτομο (μαθητή) γίνονται δύο μετρήσεις. Δηλαδή το δείγμα αποτελείται από τα ζεύγη τιμών των συνεχών μεταβλητών X (ύψος) και Y (βάρος).
Αν παραστήσουμε τα ζεύγη (x, y) των παρατηρήσεων σε ένα σύστημα ορθογώνιων αξόνων, παρατηρούμε ότι προκύπτει μία “διασπορά” των σημείων που αντιστοιχούν στους μαθητές που εξετάζουμε. Η παράσταση αυτή των σημείων καλείται διάγραμμα διασποράς (scatter diagram), βλέπε σχήμα 16.

Διάγραμμα διασποράς και ευθεία προσαρμοσμένη “με το μάτι”
για τα δεδομένα του πίνακα 10.

Η προσεκτική παρατήρηση ενός διαγράμματος διασποράς μπορεί να μας δώσει σημαντικές πληροφορίες για τη σχέση εξάρτησης που ενδεχομένως υπάρχει μεταξύ των μεταβλητών τις οποίες εξετάζουμε. Η πείρα μας λέει ότι υπάρχει κάποια σχέση μεταξύ του ύψους και του βάρους κάθε μαθητή. Στο παράδειγμα αυτό το διάγραμμα διασποράς δείχνει, γενικά, ότι οι ψηλοί μαθητές είναι συνήθως και πιο βαρείς. Για παράδειγμα, ο Ν είναι ψηλότερος και βαρύτερος από τον Κ, ο Π είναι ψηλότερος και βαρύτερος από τον Κ, αλλά υπάρχουν και εξαιρέσεις, όπως ο Π είναι ψηλότερος από τον Ν αλλά ο Ν είναι βαρύτερος από τον Π.

Ευθεία Παλινδρόμησης

Από το διάγραμμα διασποράς του προηγούμενου παραδείγματος φαίνεται καθαρά ότι υπάρχει μία σχέση ανάμεσα στο ύψος Χ και το βάρος Υ των 18 αγοριών της Γ'Λυκείου. Τα σημεία (x, y) είναι συγκεντρωμένα περίπου γύρω από μία ευθεία, δηλαδή η σχέση μεταξύ των X και Y είναι κατά προσέγγιση γραμμική. Όπως έχουμε ήδη αναφέρει, μπορούμε να θεωρήσουμε τη μία μεταβλητή ως ανεξάρτητη μεταβλητή και την άλλη ως εξαρτημένη. Εδώ θεωρούμε ως ανεξάρτητη μεταβλητή το ύψος X και ως εξαρτημένη μεταβλητή το βάρος Y, οπότε η ευθεία που θα προσαρμόζεται καλύτερα στα σημεία αυτά καλείται ευθεία παλινδρόμησης της Y πάνω στη X.
Όπως γνωρίζουμε, η εξίσωση μιας ευθείας δίνεται από τη σχέση:

y = α + βx                            (1)

όπου α και β είναι παράμετροι τις οποίες θέλουμε να υπολογίσουμε ή, όπως λέμε, να “εκτιμήσουμε”, έτσι ώστε η ευθεία που θα προκύψει να μας δίνει όσο το δυνατόν την καλύτερη περιγραφή της σχέσης (εξάρτησης) που υπάρχει μεταξύ των μεταβλητών X και Y.

Η παράμετρος α μας δίνει το σημείο (0,α), όπου η ευθεία αυτή τέμνει τον άξονα y'y, ενώ η παράμετρος β παριστάνει το συντελεστή διεύθυνσης της ευθείας.
Ο πιο εύκολος τρόπος χάραξης της ευθείας είναι αυτός που γίνεται “με το μάτι”. Μια τέτοια ευθεία έχουμε φέρει και στο διάγραμμα διασποράς του σχήματος 16. Για να βρούμε τα α και β, εργαζόμαστε ως εξής:

• Επιλέγουμε δύο σημεία, έστω τα Γ(173,67) και Σ(191,86) πάνω στην ευθεία που φέραμε “με το μάτι”.
  
  
• Αντικαθιστούμε τις συντεταγμένες (x, y) των σημείων αυτών στην (1), οπότε προκύπτει το σύστημα:
  
  

  
  

• Επιλύοντας το σύστημα αυτό βρίσκουμε α = -115,6 και β = 1,06 οπότε η εξίσωση της ευθείας (1) γίνεται:
  
  

  y = -115,6 + 1,06                            (2)

Επομένως, η ευθεία που κατά τη γνώμη μας προσαρμόζεται καλύτερα στα σημεία του διαγράμματος διασποράς διέρχεται από το σημείο (0 , -115,6) και έχει συντελεστή διεύθυνσης 1,06.

Μέθοδος των Ελαχίστων Τετραγώνων

Είδαμε ότι η πιο απλή διαδικασία προσαρμογής μιας ευθείας γραμμής σε ένα διάγραμμα διασποράς είναι “με το μάτι”. Αυτή όμως έχει πολλά μειονεκτήματα παρά την απλότητά της. Το κυριότερο είναι η έλλειψη αντικειμενικότητας, αφού διάφορα άτομα μπορούν να χαράξουν διαφορετικές μεταξύ τους ευθείες. Ακόμα και το ίδιο άτομο μπορεί να χαράζει διαφορετικές ευθείες κάθε φορά. Χρειαζόμαστε λοιπόν μια ακριβέστερη μέθοδο για την προσαρμογή μιας ευθείας γραμμής σε τέτοιου είδους δεδομένα.
Μιά μέθοδος που χρησιμοποιείται για την εκτίμηση των παραμέτρων α και β, άρα και για την εύρεση της εξίσωσης της καλύτερης ευθείας που προσαρμόζεται στα δεδομένα, είναι η “μέθοδος ελαχίστων τετραγώνων”. Η πρώτη αναφορά με ολοκληρωμένη ανάπτυξη της μεθόδου των ελαχίστων τετραγώνων εμφανίζεται το 1805 σε μια εργασία του Γάλλου μαθηματικού Legendre, (1752-1833) και αμέσως μετά από το Γερμανό μαθηματικό Gauss, (1777-1855) στην αστρονομική του πραγματεία “Theoria Motus” για τον προσδιορισμό της τροχιάς του μικρού πλανήτη Δήμητρα.

Μάλιστα εδώ ο Gauss αναφέρει ότι χρησιμοποίησε την αρχή των ελαχίστων τετραγώνων πριν από το 1794 (σε ηλικία μόλις 17 ετών), έτσι ώστε να προηγείται του Legendre ως προς την ανακάλυψη αυτής της μεθόδου. Ας δούμε ξανά το διάγραμμα διασποράς στο σχήμα 17 του προηγούμενου παραδείγματος για τα ύψη Χ και τα βάρη Υ των 18 μαθητών του πίνακα 10. Στο διάγραμμα αυτό έχουμε φέρει και μία ευθεία y = α + βx, που πιστεύουμε ότι προσαρμόζεται καλύτερα στα σημεία (x_i , y_i) για τις v = 18 συνολικά μετρήσεις των μεταβλητών Χ και Υ.

Προσαρμογή ευθείας ελαχίστων τετραγώνων στο διάγραμμα διασποράς
των δεδομένων του πίνακα 10.

Έτσι, για παράδειγμα, για το μαθητή Β, σημείο B(172,60), με ύψος x₂ = 172 cm έχουμε βρει, όπως φαίνεται στον πίνακα 10, βάρος y₂ = 60kg, ενώ, σύμφωνα με την ευθεία που φέραμε, το βάρος του αναμένεται να είναι (περίπου) 64kg, έχουμε δηλαδή ένα σφάλμα ε₂ = 60 - 64 = -4, δηλαδή βάρος 4kg λιγότερο από το αναμενόμενο. Ομοίως για το μαθητή Ζ, σημείο Z(177,81), το βάρος του που μετρήθηκε ήταν y₆ = 81kg, ενώ το αναμενόμενο βάρος του σύμφωνα με την ευθεία που φέραμε είναι 71kg, έχουμε δηλαδή ένα σφάλμα ε₆ = 81- 71 = 10, δηλαδή βάρος 10kg περισσότερο από το αναμενόμενο. Ανάλογα σφάλματα υπολογίζονται και για τους άλλους μαθητές. Θα θέλαμε λοιπόν να βρούμε με κάποια μέθοδο εκείνη την ευθεία y = α + βx, έτσι ώστε τα σφάλματα που προκύπτουν να είναι όσο το δυνατόν μικρότερα.
Η μέθοδος των ελαχίστων τετραγώνων συνίσταται στον προσδιορισμό των παραμέτρων α, β, έτσι ώστε να ελαχιστοποιείται το άθροισμα των τετραγώνων των κατακόρυφων αποστάσεων των σημείων (x_i , y_i) από την ευθεία y = α + βx, δηλαδή το

να γίνεται ελάχιστο.

Οι τιμές των παραμέτρων α και β, που ελαχιστοποιούν την (4), καλούνται εκτιμήτριες ελαχίστων τετραγώνων (least square estimators), συμβολίζονται με (“α καπέλο”) και (“β καπέλο”), αντιστοίχως, και αποδεικνύεται (η απόδειξη εδώ παραλείπεται) ότι δίνονται από τις σχέσεις:

όπου

Η ευθεία

καλείται ευθεία ελαχίστων τετραγώνων ή ευθεία παλινδρόμησης της Υ (πάνω) στη Χ. Αντικαθιστώντας το στη σχέση (6) βρίσκουμε την

η οποία φανερώνει ότι η ευθεία ελαχίστων τετραγώνων διέρχεται από το σημείο με συντεταγμένες και έχει συντελεστή διεύθυνσης το Αντικαθιστώντας τις τιμές x_i και y_i από τον πίνακα 10 στις σχέσεις (5) βρίσκουμε:

οπότε η ευθεία ελαχίστων τετραγώνων που προσαρμόζεται καλύτερα στα δεδομένα είναι από τη σχέση (6), η

Παρατηρούμε ότι υπάρχει σημαντική διαφορά από την ευθεία y = -115,6 + 1,06x που προσαρμόσαμε “με το μάτι” στο σχήμα 16.

Ερμηνεία των

Στην εξίσωση ελαχίστων τετραγώνων η τιμή της εκτιμήτριας της παραμέτρου α παριστάνει την τεταγμένη του σημείου στο οποίο η ευθεία τέμνει τον άξονα y'y, δηλαδή την τιμή της εξαρτημένης μεταβλητής Υ όταν x = 0. Όταν το τότε η ευθεία διέρχεται από την αρχή των αξόνων.
Έστω τώρα δυο τιμές x₁ και x₂ = x₁ + 1 της ανεξάρτητης μεταβλητής. Τότε λαμβάνοντας τη διαφορά των αντίστοιχων προβλεπόμενων τιμών της εξαρτημένης μεταβλητής βρίσκουμε

δηλαδή Συνεπώς ο συντελεστής διεύθυνσης της ευθείας παριστά τη μεταβολή της εξαρτημένης μεταβλητής Υ όταν το Χ μεταβληθεί κατά μια μονάδα. Έτσι, όταν το x αυξηθεί κατά μια μονάδα τότε το αυξάνεται κατά μονάδες όταν ή ελαττώνεται κατά μονάδες όταν

ΕΦΑΡΜΟΓΕΣ

1. Ένας ερευνητής, για να εξετάσει την επίδραση ενός αναισθητικού, εμβολίασε 10 ποντίκια με διαφορετική δόση κάθε φορά. Οι χρόνοι που μεσολάβησαν ώσπου τα ποντίκια να χάσουν τις αισθήσεις τους (λιποθυμήσουν) καταγράφονται στον παρακάτω πίνακα.

α) Να γίνει το διάγραμμα διασποράς
β) Να επιλεγούν δύο πιθανά σημεία από τα οποία διέρχεται η προσαρμοσμένη ευθεία παλινδρόμησης και με βάση αυτά να βρεθεί η εξίσωση της ευθείας.
γ) Ύστερα από πόσο χρόνο αναμένεται να λιποθυμήσει ένα ποντίκι, εάν του γίνει ένεση (εμβολιαστεί) με 0, 0,5, 1 mgr αναισθητικού, αντίστοιχα; Να σχολιαστούν τα αποτελέσματα.

ΛΥΣΗ

α) Η περίπτωση που εξετάζεται εδώ αναφέρεται σε μια πειραματική κατάσταση, κατά την οποία ο ερευνητής καθορίζει εκ των προτέρων τη δόση του αναισθητικού που θα δώσει στα πειραματόζωα και μετρά τις αντιδράσεις τους. Ενδιαφέρεται δηλαδή να προσδιορίσει μια σχέση δόσης αναισθητικού και χρόνου λιποθυμίας. Έτσι, η δόση αναισθητικού παριστάνει την ανεξάρτητη μεταβλητή (X) και ο χρόνος λιποθυμίας την εξαρτημένη μεταβλητή (Y). Επομένως, το διάγραμμα διασποράς παριστάνεται παρακάτω:

β) Δύο σημεία από τα οποία εκτιμάται “με το μάτι” ότι θα διέρχεται η καλύτερη ευθεία παλινδρόμησης είναι τα A(0,3 , 12,3) και B(0,8 , 1,9) . Αντικαθιστώντας στην εξίσωση της ευθείας y = α + βx έχουμε το σύστημα:

από την επίλυση του οποίου βρίσκουμε α = 18,5 και β = -20,8, οπότε η ευθεία παλινδρόμησης έχει εξίσωση

y = 18,5 - 20,8x.

Παρατηρούμε, όπως άλλωστε αναμενόταν και από το διάγραμμα διασποράς, ότι ο συντελεστής διεύθυνσης είναι αρνητικός, δηλαδή έχουμε αρνητική εξάρτηση του χρόνου λιποθυμίας ως προς τη δόση αναισθητικού. Μεγαλύτερη δόση επιφέρει γρηγορότερη (σε μικρότερο χρόνο) λιποθυμία.
γ) Αντικαθιστώντας στην παραπάνω εξίσωση τις τιμές της δόσης x = 0, 0,5 και 1 mgr, βρίσκουμε τον προβλεπόμενο χρόνο λιποθυμίας του ποντικιού y = 18,5, 8,1 και -2,3 sec, αντίστοιχα.

ΣΧΟΛΙΟ

Παρατηρούμε ότι εμφανίζονται εδώ δυο παράδοξα:

• Μηδενική δόση του αναισθητικού προκαλεί λιποθυμία σε 18,5 sec. Υποθέτουμε όμως εδώ ότι τα ποντίκια χάνουν τις αισθήσεις τους μόνο από τη δόση του αναισθητικού και όχι από το φόβο τους!
• Δόση αναισθητικού 1 mgr προκαλεί λιποθυμία σε 2,3 sec. Όμως και πάλι εδώ υποθέτουμε ότι η ένεση γίνεται σε ποντίκι που έχει τις αισθήσεις του και όχι να είναι πριν από 2,3 sec λιπόθυμο!
• Οι δύο αυτές παρατηρήσεις οδηγούν στο βασικό συμπέρασμα ότι οι προβλέψεις της εξαρτημένης μεταβλητής έχουν νόημα, είναι δηλαδή δυνατές, μόνο για τις τιμές της ανεξάρτητης μεταβλητής οι οποίες βρίσκονται στο διάστημα που έχουμε εξετάσει ή τουλάχιστον πολύ κοντά στα άκρα του διαστήματος αυτού.

2. Ο παρακάτω πίνακας δίνει τις πωλήσεις (ζήτηση) ενός προϊόντος (π.χ. των κερασιών) Υ (σε κιλά) από το μανάβικο μιας περιοχής και τις αντίστοιχες τιμές Χ του προϊόντος σε εκατοντάδες δρχ. ανά κιλό για μια ορισμένη χρονική περίοδο

α) Να βρεθεί η ευθεία ελαχίστων τετραγώνων (των πωλήσεων σε συνάρτηση με την τιμή) και να χαραχτεί στο αντίστοιχο διάγραμμα διασποράς.
β) Να ερμηνευθεί η έννοια των
γ) Ποια είναι η αναμενόμενη ζήτηση (πωλήσεις), όταν η τιμή είναι 800 δρχ./κιλό;
δ) Με βάση την ευθεία αυτή μπορούμε να προβλέψουμε την τιμή του προϊόντος, όταν η ζήτηση είναι 10 κιλά;

ΛΥΣΗ

α) Για τον προσδιορισμό της εξίσωσης της ευθείας ελάχιστων τετραγώνων διευκολύνει ο διπλανός πίνακας με τις απαραίτητες πράξεις. Επομένως, έχουμε: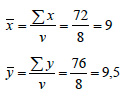
ν = 8

Άρα, η εξίσωση της ζήτησης (των κερασιών) σε συνάρτηση με την τιμή τους είναι

Επειδή γνωρίζουμε ότι η ευθεία που διέρχεται από τα σημεία (0,α) και είναι εύκολο να χαραχτεί στο διάγραμμα διασποράς, όπως φαίνεται δίπλα.
β) Το προσδιορίζει την προβλεπόμενη ζήτηση του προϊόντος, όταν η τιμή του είναι 0 δρχ./κιλό. Προφανώς εδώ τέτοια περίπτωση δεν είναι ρεαλιστική.
Το β προσδιορίζει τη μεταβολή που επέρχεται στην εξαρτημένη μεταβλητή Υ, όταν η Χ μεταβληθεί κατά μία μονάδα. Δηλαδή όταν η τιμή των κερασιών αυξηθεί κατά 100 δρχ./κιλό (μία μονάδα), οι πωλήσεις θα ελαττωθούν κατά 0,76 κιλά.
γ) Όταν η αξία του προϊόντος είναι 800 δρχ./κιλό, σημαίνει ότι x = 8 (8 εκατοντάδες δρχ.). Συνεπώς, για x = 8 η αναμενόμενη ζήτηση y είναι = 16,34 - 0,76 · 8 = 16,34 - 6,08 = 10,26 κιλά.
δ) Προφανώς, στην περίπτωση που χρησιμοποιείται η μέθοδος των ελαχίστων τετραγώνων για την εκτίμηση της ευθείας παλινδρόμησης της εξαρτημένης μεταβλητής Υ πάνω στην ανεξάρτητη μεταβλητή Χ, δεν μπορεί να χρησιμοποιηθεί η προκύπτουσα ευθεία για πρόβλεψη της Χ, όταν δίνεται το Υ. Για να γίνει κάτι τέτοιο, πρέπει εξαρχής να εκτιμηθεί η ευθεία παλινδρόμησης της Χ πάνω στην Υ.

Ασκήσεις