1.3 ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ

Ορισμός Παραγώγου

Έστω μια συνάρτηση f με πεδίο ορισμού το Α, και Β το σύνολο των x∈A στα οποία η f είναι παραγωγίσιμη. Τότε ορίζεται μια νέα συνάρτηση, με την οποία κάθε x∈B αντιστοιχίζεται στο Εικόνα Η σ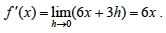υνάρτηση αυτή λέγεται (πρώτη) παράγωγος (derivative) της f και συμβολίζεται με f '.

Για παράδειγμα, αν f(x)=3x², τότε έχουμε:
f(x + h) - f(x)=3(x + h)² - 3x²=3(x² + 2xh + h² - x²)=3h(2x + h),
και για h≠0

Εικόνα

Επομένως,

Έτσι, η παράγωγος μιας συνάρτησης f στο x₀ είναι ίση με την τιμή της παραγώγου της συνάρτησης στο σημείο αυτό. Για παράδειγμα, η παράγωγος της f(x)=3x² στο x₀=4 είναι ίση με την τιμή της συνάρτησης f '(x)=6x στο x₀=4, δηλαδή f '(4)=6·4=24.
Η παράγωγος της συνάρτησης f ' λέγεται δεύτερη παράγωγος της f και συμβολίζεται με f ''.
Σύμφωνα με τα προηγούμενα αν η τετμημένη ενός κινητού που κινείται ευθυγράμμως είναι x(t) τη χρονική στιγμή t, τότε η ταχύτητά του θα είναι

υ(t)=x'(t)

Αν η συνάρτηση υ είναι παραγωγίσιμη, τότε η επιτάχυνση του κινητού τη χρονική στιγμή t θα είναι η παράγωγος της ταχύτητας, δηλαδή θα ισχύει

α(t)=υ'(t) ή ισοδύναμα α(t)=x''(t)

Παραγώγιση Βασικών Συναρτήσεων

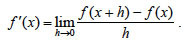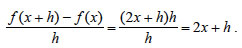Έως τώρα η παραγώγιση μιας συνάρτησης f γινόταν με τη βοήθεια του τύπου Εικόνα

Στη συνέχεια θα γνωρίσουμε μερικούς κανόνες που διευκολύνουν τον υπολογισμό της παραγώγου πιο πολύπλοκων συναρτήσεων.

Εικόνα

Η παράγωγος της σταθερής συνάρτησης f(x)=c

Έχουμε
f(x + h) - f (x) = c - c = 0

και για h≠0

οπότε

Άρα (c)'=0.
Η παράγωγος της ταυτοτικής συνάρτησης f(x) = x

Έχουμε f(x + h) - f(x) = (x + h) - x = h , και για h ≠ 0,

Επομένως
Άρα, (x)'=1.
Η παράγωγος της συνάρτησης f (x) = x^ρ

Έστω η συνάρτηση f (x) = x². Έχουμε
f (x + h) - f (x) = (x + h)² - x² = x² + 2xh + h² - x² = (2x + h)h,

και για h≠0, Εικόνα

Επομένως,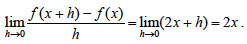

Άρα (x²)' = 2x

Εικόνα

Αποδεικνύεται ότι

(xν)' = ν x ^ν-1, όπου ν φυσικός.

Ο τύπος αυτός ισχύει και στην περίπτωση που ο εκθέτης είναι ρητός αριθμός.
Για παράδειγμα

Εικόνα

Άρα

(x^ρ) = ρ x^ρ-1, όπου ρ ρητός αριθμός.

Η παράγωγος του ημx και του συνx.

Έστω η γραφική παράσταση της συνάρτησης f(x)=ημx (σχήμα 15). Αν λάβουμε υπόψη ότι η τιμή της f '(x) σε ένα σημείο x = x₀ είναι ο συντελεστής διεύθυνσης της εφαπτομένης της καμπύλης της f στο σημείο (x₀, f(x₀)), μπορούμε να σχεδιάσουμε προσεγγιστικά τη γραφική παράσταση της f '. Παρατηρούμε ότι η γραφική παράσταση της f ' μοιάζει με τη γραφική παράσταση της συνάρτησης συνx.

Εικόνα

Πράγματι, για τη συνάρτηση f(x) = ημx αποδεικνύεται ότι

(ημx)'= συνx.

Επίσης για τη συνάρτηση g(x) = συνx αποδεικνύεται ότι

(συνx)'= -ημx.

Η παράγωγος του e^x και του lnx.

Για την εκθετική και τη λογαριθμική συνάρτηση, με βάση τον αριθμό e, αποδεικνύεται ότι
(e^x)' = e^x και

Κανόνες Παραγώγισης

Η παράγωγος της συνάρτησης cf(x)

Έστω η συνάρτηση F(x) = cf(x). Έχουμε
F(x + h) - F(x) = cf (x + h) - cf (x) = c(f(x + h) - f(x)), και για h ≠ 0

Επομένως

Άρα (c · f(x))' = c · f'(x).

Για παράδειγμα (3x⁵)' = 3(x⁵)' = 3 · 5x⁴ = 15x⁴,

Εικόνα

και

Εικόνα

Η παράγωγος τηςσυνάρτησης f(x) + g(x).

Έστω η συναρτηση F(x) = f(x) + g(x). Έχουμε
F(x + h) - F(x) = (f(x + h) + g(x + h)) - (f(x) + g(x))
= ( f(x + h) - f(x)) + (g(x + h) - g(x)),

και για h≠0,
Επομένως

Άρα             (f(x) + g(x))' = f'(x) + g'(x)

Για παράδειγμα             (x⁴ + 3x)' = (x⁴)' + (3x)' = 4x³ + 3
και

Παράγωγος των συναρτήσεων f(x) · g(x) και
Για το γινόμενο και το πηλίκο συναρτήσεων αποδεικνύεται ότι ισχύουν οι παρακάτω κανόνες παραγώγισης:

Για παράδειγμα

(x · ημx)' = (x)'ημx + x(ημx)' = ημx + x · συνx

και

Εικόνα

Η παράγωγος σύνθετης συνάρτησης.

Γνωρίζουμε ήδη πώς παραγωγίζονται οι συναρτήσεις x^ν, ημx, συνx, e^x και lnx. Επίσης, με τη βοήθεια των κανόνων παραγώγισης αθροίσματος, γινομένου και πηλίκου μπορούμε να παραγωγίσουμε και πολυπλοκότερες συναρτήσεις όπως για παράδειγμα τις (x³ + 1)² και (x³ + 1)³ για τις οποίες έχουμε

((x³ + 1)²)' = ((x³ +1)(x³ +1))' = 3x²(x³ +1) +3x²(x³ +1) = 6x²(x³ + 1) και

((x³ + 1)³)' = [(x³ + 1)²(x³ + 1)]' = 6x²(x³ + 1)(x³ + 1) +(x³ + 1)² · 3x² = 9x²(x³ + 1)²

Πώς όμως θα παραγωγίσουμε μια συνάρτηση όπως η
Παρατηρούμε ότι η συνάρτηση F(x) προκύπτει αν στην f(x) = √ x θέσουμε όπου x το g(x) = x² + 1. Είναι, δηλαδή, Γι’ αυτό η συνάρτηση F λέγεται σύνθεση της g με την f.
Αποδεικνύεται ότι για την παράγωγο μιας σύνθετης συνάρτησης ισχύει:

(f(g(x)))' = f '(g(x)) · g'(x).

Δηλαδή για να παραγωγίσουμε τη συνάρτηση f(g(x)), σε πρώτη φάση παραγωγίζουμε την f σαν να έχει ανεξάρτητη μεταβλητή την g(x) και στη συνέχεια πολλαπλασιάζουμε με την παράγωγο της g. Επομένως,

((x³ + 1)³)' = 3(x³ +1)²(x³ +1))' = 3(x³ +1)² · 3x² = 9x²(x³ + 1)².

Επίσης, επειδή όπως είδαμε, είναι έχουμε:

Ομοίως, (ημ(2x + 1))' = συν(2x + 1) · (2x + 1)' = 2 · συν(2x + 1).

Στον παρακάτω πίνακα συνοψίζονται οι βασικοί τύποι και κανόνες παραγώγισης.

ΕΦΑΡΜΟΓΕΣ

1. Να υπολογιστεί η παράγωγος των συναρτήσεων
i) f(x) = εφx ii) f(x) = ημ²3x.

ΛΥΣΗ

i) Έχουμε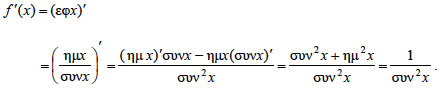

Άρα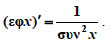

ii) Έχουμε

f'(x) = [(ημ3x)²]' = 2 · ημ3x · (ημ3x)' = 2 · ημ3x · συν3x · (3x)'
= 3 · 2ημ3x · συν3x = 3 · ημ(2 · 3x) = 3ημ6x,

όπου χρησιμοποιήθηκε η σχέση ημ2α = 2ημα συνα.

2. Η θέση ενός υλικού σημείου, το οποίο εκτελεί ευθύγραμμη κίνηση δίνεται από τον τύπο x = x(t) = t³- 6t²+ 9t, όπου το t μετριέται σε δευτερόλεπτα και το x σε μέτρα.
i) Να βρεθεί η ταχύτητα του σημείου σε χρόνο t.
ii) Ποια είναι η ταχύτητα του σημείου σε χρόνο 2 s και ποια σε χρόνο 4 s;
iii) Πότε το σημείο είναι (στιγμιαία) ακίνητο;
iv) Πότε το σημείο κινείται στη θετική κατεύθυνση και πότε στην αρνητική κατεύθυνση;
v) Να βρεθεί το ολικό διάστημα που έχει διανύσει το σημείο στη διάρκεια των πρώτων 5 s.

ΛΥΣΗ

i) Η ταχύτητα είναι

υ(t) = x'(t) = (t³ - 6t² + 9t)' = 3t² - 12t + 9.

ii) Η ταχύτητα του σημείου
σε χρόνο t = 2s είναι υ(2) = 3 · 2² -12 · 2 + 9 = -3 m/s
και σε χρόνο t = 4s είναι υ(4) = 3 · 4² -12 · 4 + 9 = 9 m/s.

iii) Το σημείο είναι ακίνητο, όταν υ(t) = 0, δηλαδή όταν

3t² - 12t + 9 = 0
t² - 4t + 3 = 0
t =1 ή t = 3.

Άρα, το σημείο είναι ακίνητο ύστερα από 1 s και ύστερα από 3 s.

iv) Το σημείο κινείται στη θετική κατεύθυνση, όταν υ(t) > 0, δηλαδή όταν

3t² - 12t + 9 > 0
t² - 4t + 3 > 0
(t - 1)(t - 3) > 0
t < 1 ή t > 3.

Άρα, το σημείο κινείται στη θετική κατεύθυνση στα χρονικά διαστήματα t < 1 και t > 3 (και στην αρνητική κατεύθυνση όταν 1 < t < 3).
Σχηματικά η κίνηση του υλικού σημείου μπορεί να παρασταθεί ως εξής:

Εικόνα

v) Η απόσταση που διανύθηκε από το κινούμενο σημείο είναι:

Στη διάρκεια του πρώτου δευτερόλεπτου
S₁ = |x(1) - x(0)| = |4 - 0|= 4m.
Από t = 1 μέχρι t = 3
S₂ = |x(3) - x(1)| = |0 - 4|= 4m.
Από t = 3 μέχρι t = 5
S₃ = |x(5) - x(3)| = |20 - 0|= 20m.

Άρα, το ολικό διάστημα S που διάνυσε το σημείο σε χρόνο 5s είναι

S = S₁ + S₂ + S₃ = 4 + 4 + 20 = 28 m.

Ασκήσεις

Α' ΟΜΑΔΑΣ
	(Να βρείτε τις παραγώγους των συναρτήσεων στις ασκήσεις 1-18)
1.	i) f(x)=-5		ii) f(x)=x⁴	iii) f(x)=x⁹
2.	i) f(x)=x^3/2		ii) f(x)=x^-3	iii) f(x)=x^-5
3.	i) f(x)=		ii) f(x)= x > 0.
4.	i) f(x)=		ii) f(x)=	iii) f(x)= x > 0.
5.	i) f(x)=4x³		ii) f(x)=6x^-5	iii) f(x)=
6.	i) f(x)=		ii) f(x)=6x√x.
7.	i) f(x)=4x⁴ + 3x²		ii) f(x)=x² + 5 +	iii) f(x)=
8.	i) f(x)=8x³ - ημx + 5		ii) f(x)=6συνx - 8(x² + x).
9.	i) f(x)=(x³ + 1)((x⁴ + 1)		ii) f(x)=ημx(1 - συνx).
10.	i) f(x)=xσυνx + 3(x + 1)(x - 1)		ii) f(x)=4x²ημx - 3x²συνx).
11.	i) f(x)=		ii) f(x)=	iii) f(x)=
12.	i) f(x)=		ii) f(x)=
13.	i) f(x)=(x - 1)⁵		ii) f(x)=(2x + 1)⁵	iii) f(x)=(2x² - 3x)⁵.
14.	i) f(x)=ημ³x	ii) f(x)=ημx³	iii) f(x)=x · ημ4x	iv) f(x)=εφ3x.
15.	i) f(x)=		ii) f(x)=
16.	i) f(x)=e^3x	ii) f(x)=	iii) f(x)=e^αx+β	iv) f(x)=

17.
18.	i) f(x)=	ii) f(x)=e^xlnx.
19.	i) Να βρείτε το συντελεστή διεύθυνσης της εφαπτομένης της καμπύλης της συνάρτησης στο σημείο της A(3, f (3)). ii) Ομοίως της καμπύλης της συνάρτησης στο σημείο της
20.	Το βάρος Β σε γραμμάρια ενός θηλυκού ποντικιού ύστερα από t εβδομάδες δίνεται προσεγγιστικά από τη συνάρτηση , όπου t ≤ 8. Να βρείτε το ρυθμό ανάπτυξης του ποντικιού: i) ύστερα από t εβδομάδες και ii) ύστερα από 1, 2 και 8 εβδομάδες.
21.	Να βρείτε το ρυθμό μεταβολής της απόστασης των σημείων A(0,3) και B(x,0) ως προς x όταν x = 10.
22.	Να βρείτε την τιμή του α ώστε η εφαπτομένη της γραφικής παράστασης της συνάρτησης f(x) = αx(1 - x) στο σημείο της O(0, f (0)) να σχηματίζει με τον άξονα x'x γωνία 60°.

Β' ΟΜΑΔΑΣ
1.	Σε ποιά σημεία της καμπύλης της συνάρτησης η εφαπτομένη της είναι παράλληλη στην ευθεία y = 3x + 5;
2.	Να βρείτε τα σημεία της καμπύλης της συνάρτησης f(x) = x³ - 6x² + 9x + 4 στα οποία οι εφαπτόμενες είναι παράλληλες στον άξονα x'x.
3.	Να βρείτε τις εξισώσεις των εφαπτομένων της γραφικής παράστασης της που είναι παράλληλες στη διχοτόμο της γωνίας .
4.	Ένα σώμα κινείται σε έναν άξονα έτσι ώστε η θέση του σε χρόνο t να δίνεται από τον τύπο x(t) = t³ - 2t² + t. Να βρείτε την ταχύτητα του σώματος σε χρόνο t και να προσδιορίσετε πότε το σώμα είναι ακίνητο. Ποια είναι η επιτάχυνση του σώματος στις χρονικές αυτές στιγμές;
5.	Αν f(x) = Aσυνωx + Bημωx, να δείξετε ότι f''(x) + ω² f(x) = 0.
6.	Αν f(x) = αe^px + βe^-px, να δείξετε ότι f''(x) = p²f(x).
7.	Αν f(x) = e^μx, να βρείτε το μ ώστε να ισχύει f''(x) - 3f'(x) - 4f(x) = 0.
8.	Να βρείτε την εξίσωση της εφαπτομένης της καμπύλης της συνάρτησης f(x) = 2ημx · συνx στο σημείο της με
9.	Ο ρυθμός της φωτοσύνθεσης P ενός φυτού δίνεται από τον τύπο I ≥ 0, όπου Ι η ένταση του φωτός και α, β σταθερές. i) Να βρείτε την P'(I) ή, όπως λέγεται, τη φωτοχημική ικανότητα του φυτού, καθώς και την P'(0). ii) Να δείξετε ότι
10.	Η θέση ενός υλικού σημείου που κινείται σε έναν κατακόρυφο άξονα δίνεται από τον τύπο y(t) = Aημωt, όπου t ο χρόνος και τα Α, ω σταθερές. i) Να βρείτε την ταχύτητα και την επιτάχυνση του σημείου ως συνάρτηση του t. ii) Να δείξετε ότι η επιτάχυνση είναι ανάλογη της απομάκρυνσης y. iii) Να δείξετε ότι, όταν η επιτάχυνση είναι 0, το μέτρο της ταχύτητας είναι μέγιστο.