1.4 ΕΦΑΡΜΟΓΕΣ ΤΩΝ ΠΑΡΑΓΩΓΩΝ

Το Κριτήριο της Πρώτης Παραγώγου

Σε προηγούμενες τάξεις χρειάστηκε να εφαρμόσουμε τις μεθόδους της Άλγεβρας και της Γεωμετρίας για να επιλύσουμε προβλήματα στα οποία σκοπός ήταν να μεγιστοποιήσουμε ή να ελαχιστοποιήσουμε την τιμή ενός μεγέθους. Για παράδειγμα, μεταξύ όλων των ορθογωνίων με την ίδια περίμετρο βρήκαμε τις διαστάσεις εκείνου του ορθογωνίου που έχει το μέγιστο εμβαδόν και μεταξύ όλων των ορθογωνίων με το ίδιο εμβαδόν, αναζητήσαμε τις διαστάσεις εκείνου του ορθογωνίου που έχει την ελάχιστη περίμετρο. Βέβαια οι μέθοδοι που χρησιμοποιήσαμε για την επίλυση των προβλημάτων αυτών δύσκολα μπορούν να εφαρμοστούν και για την επίλυση προβλημάτων άλλης μορφής. Με τη βοήθεια όμως της παραγώγου μπορούμε να διατυπώσουμε μια γενική μέθοδο προσδιορισμού της μέγιστης ή της ελάχιστης τιμής ενός μεταβαλλόμενου μεγέθους.
Ας υποθέσουμε, για παράδειγμα, ότι θέλουμε να βρούμε το μέγιστο ύψος στο οποίο μπορεί να φθάσει ένα σώμα που εκτοξεύεται κατακόρυφα προς τα επάνω με αρχική ταχύτητα υ₀ = 20m/s. Αν η επιτάχυνση της βαρύτητας είναι g = 10m/s², τότε, σύμφωνα με όσα μας διδάσκει η Φυσική, το ύψος h του σώματος ύστερα από t δευτερόλεπτα θα είναι

h(t) = 20t - 5t² = -5t² + 20t. (1)

Εικόνα

Επομένως η γραφική παράσταση της h(t) θα είναι μια παραβολή η οποία:

Τέμνει τον άξονα των t στα σημεία t = 0 και t = 4.
Παρουσιάζει μέγιστο για που είναι ίσο με h(2) = 20.
Είναι γνησίως αύξουσα για t < 2 και γνησίως φθίνουσα για t > 2.

Ας δούμε τώρα πώς μεταβάλλεται το πρόσημο της παραγώγου h'(t) = -10t + 20 στο διάστημα [0, 4].
Λύνοντας την ανίσωση h'(t) > 0, βρίσκουμε ότι αριστερά του 2 όπου η συνάρτηση είναι γνησίως αύξουσα, η παράγωγός της είναι θετική, ενώ δεξιά του 2 όπου η συνάρτηση είναι φθίνουσα, η παράγωγός της είναι αρνητική.

Εικόνα

Από τα παραπάνω φαίνεται να υπάρχει στενή σχέση ανάμεσα στη μονοτονία και στην παράγωγο μιας συνάρτησης.

Αποδεικνύεται ότι:

Αν μια συνάρτηση f είναι παραγωγίσιμη σε ένα διάστημα Δ και ισχύει f '(x) > 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα στο Δ.
Αν μια συνάρτηση f είναι παραγωγίσιμη σε ένα διάστημα Δ και ισχύει f '(x) < 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως φθίνουσα στο Δ.

Παρατηρούμε ακόμα ότι στο σημείο t = 2 όπου η h παρουσιάζει μέγιστο, η h' μηδενίζεται, ενώ εκατέρωθεν του t = 2 η h' αλλάζει πρόσημο.

Αποδεικνύεται ότι:

Αν για μια συνάρτηση f ισχύουν f '(x₀) = 0 για x₀ ∈ (α, β),
f '(x) > 0 στο (α, x₀) και f '(x) < 0 στο (x₀, β), τότε η f παρουσιάζει στο διάστημα (α, β) για x = x₀ μέγιστο.
Αν για μια συνάρτηση f ισχύουν f '(x₀) = 0 για x₀ ∈ (α, β),
f '(x) < 0 στο (α, x₀) και f '(x) > 0 στο (x₀,β), τότε η f παρουσιάζει στο διάστημα (α, β) για x = x₀ ελάχιστο.


(α)	(β)

ΕΦΑΡΜΟΓΕΣ

1. Να βρεθούν τα ακρότατα της συνάρτησης f(x) = αx² + βx + γ, α ≠ 0.

ΛΥΣΗ

Έχουμε:
f'(x) = (αx² + βx + γ)' = 2αx + β.
f'(x) = 0 ⇔ 2αx + β = 0 ⇔ 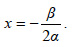Εικόνα

f'(x) > 0 ⇔ 2αx + β > 0 ⇔ 2αx > -β.

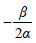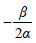Επομένως, αν α > 0, τότε f'(x) > 0 για x > Εικόνα

και f'(x) < 0 για x < Εικόνα

Εικόνα

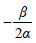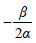ενώ αν α < 0, τότε f'(x) > 0 για x < Εικόνα

και f'(x) < 0 για x > Εικόνα

Εικόνα

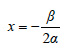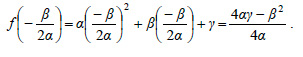Άρα, η συνάρτηση f(x) = αx² + βx + γ, α ≠ 0 για Εικόνα

παρουσιάζει ελάχιστο αν α > 0 και μέγιστο αν α < 0. Η τιμή του μεγίστου ή του ελαχίστου είναι ίση με Εικόνα

2. Ένας πληθυσμός 1000 βακτηριδίων εισάγεται σε ένα θρεπτικό μέσον και αναπτύσσεται σύμφωνα με τη συνάρτηση

Εικόνα

όπου t ο χρόνος σε ώρες. Σε πόσο χρόνο ο πληθυσμός των βακτηριδίων θα είναι μέγιστος και ποιος θα είναι ο πληθυσμός αυτός;

ΛΥΣΗ

Έχουμε

Εικόνα

Επειδή ο χρόνος t είναι θετικός, η ρίζα t = -10 απορρίπτεται.

Εικόνα

Επομένως p'(t) > 0 για 0 < t < 10.
Έχουμε λοιπόν p'(10) = 0, p'(t) > 0 στο (0, 10) και p'(t) < 0, στο (10, +∞).
Άρα ύστερα από 10 ώρες θα παρουσιαστεί ο μέγιστος πληθυσμός βακτηριδίων που θα είναι ίσος με

Εικόνα

Το Κριτήριο της Δεύτερης Παραγώγου

Εικόνα

Έστω μια συνάρτηση f, της οποίας η καμπύλη είναι μία παραβολή και η οποία για x = x₀ παρουσιάζει μέγιστο. Τότε, για τιμές κοντά στο x₀, η συνάρτηση είναι αύξουσα για x ≤ x₀ και φθίνουσα για x ≥ x₀. Αυτό σημαίνει ότι η f ' από θετική γίνεται αρνητική, δηλαδή είναι φθίνουσα συνάρτηση. Αφού λοιπόν η f ' είναι φθίνουσα, η παράγωγός της, δηλαδή η f '' θα είναι αρνητική.
Επομένως, f ''(x₀) < 0.

Εικόνα

Έστω τώρα η συνάρτηση f, της οποίας η καμπύλη είναι μια παραβολή και η οποία για x = x₀ παρουσιάζει ελάχιστο. Τότε, για τιμές του x κοντά στο x₀, η συνάρτηση είναι φθίνουσα για x ≤ x₀ και αύξουσα για x ≥ x₀. Αυτό σημαίνει ότι η f ' από αρνητική γίνεται θετική, δηλαδή είναι αύξουσα συνάρτηση. Άρα, η παράγωγος της f ', δηλαδή η f '' θα είναι θετική.
Επομένως, f ''(x₀) > 0.

Αποδεικνύεται ότι:

Αν για μια συνάρτηση f ισχύουν f '(x₀) = 0 και f ''(x₀) < 0, τότε η f παρουσιάζει (τοπικό) μέγιστο στο x₀.
Αν για μια συνάρτηση f ισχύουν f '(x₀) = 0 και f ''(x₀) > 0, τότε η f παρουσιάζει (τοπικό) ελάχιστο στο x₀.

ΣΧΟΛΙΟ

Αν για μια συνάρτηση f ισχύουν f '(x₀) = 0 και f ''(x₀) = 0, τότε δεν μπορεί να χρησιμοποιηθεί το κριτήριο της 2ης παραγώγου για τον προσδιορισμό των ακροτάτων της f.

ΕΦΑΡΜΟΓΕΣ

Εικόνα

1. Ένα παράθυρο έχει το διπλανό σχήμα και αποτελείται από ένα ορθογώνιο που περικλείεται στο άνω μέρος από ένα ημικύκλιο. Το παράθυρο έχει περίμετρο 30 μέτρα. Να βρείτε τις διαστάσεις που πρέπει να έχει ώστε να μπαίνει από αυτό όσο γίνεται περισσότερο φως.

ΛΥΣΗ

Έστω x η ακτίνα του ημικυκλίου. Τότε ΑΒ = ΓΔ = 2x. Αν ΑΔ = ΒΓ = y, έχουμε:

Η μεγαλύτερη ποσότητα φωτός θα διέρχεται από το παράθυρο, όταν το εμβαδόν του είναι μέγιστο.
Αν Ε το εμβαδόν του παραθύρου, τότε

δηλαδή
Έχουμε E'(x) = 30 - (4 + π)x και E'(x) = 0 ⇔
Επειδή E''(x) = - (4 + π) < 0, συμπεραίνουμε ότι για η συνάρτηση έχει τη μέγιστη τιμή της. Για την τιμή αυτή του x από την (1) έχουμε
και επομένως

Άρα για το παράθυρο έχει το μέγιστο εμβαδό.

2. Το κέρδος P σε ευρώ από την πώληση ενός αυτοκινήτου ορισμένου τύπου και ο χρόνος παραγωγής του t σε ώρες σχετίζονται με τον τύπο:

Εικόνα

Να βρεθεί το μέγιστο δυνατό κέρδος.

ΛΥΣΗ

Έχουμε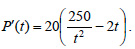

Επομένως

Εικόνα

Θα εξετάσουμε αν η τιμή t = 5 αντιστοιχεί σε μέγιστο κέρδος με τη βοήθεια της δεύτερης παραγώγου.
Έχουμε

Εικόνα

Άρα για t = 5 έχουμε το μέγιστο δυνατό κέρδος που είναι ίσο με

P(5) = 20(200 - 50 - 25) = 20 · 125 = 2500 ευρώ.

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε τα ακρότατα των συναρτήσεων
	i) f(x) = x² - 2x	ii) f(x) = -3x² + 6	iii) f(x) = x² - 2x + 4
2.	Ομοίως των συναρτήσεων
	i) f(x) = x³ - 6x + 5	ii) f(x) = -x³ + 3x + 1
3.	Να δείξετε ότι οι παρακάτω συναρτήσεις δεν έχουν ακρότατα
	i) f(x) = 2x³	ii) f(x) = -x³ + 16	iii) f(x) = x³ - 3x² + 3x - 10
	iv) f(x) = -x³ + 3x² - 5x - 11
4.	Το άθροισμα δύο αριθμών είναι ίσο με 40. Να βρείτε τη μεγαλύτερη τιμή που μπορεί να πάρει το γινόμενό τους.
5.	Από όλα τα ορθογώνια με εμβαδό 100m² ποιο είναι εκείνο που έχει τη μικρότερη περίμετρο;
6.	Ένα κουτί σχήματος ορθογωνίου παραλληλεπιπέδου με τετράγωνη βάση και ανοικτό από πάνω πρέπει να έχει όγκο 32 dm³. Να βρείτε ποιές πρέπει να είναι οι διαστάσεις του κουτιού, ώστε για την κατασκευή του να χρειάζεται το ελάχιστο δυνατό υλικό.
7.	Αν ένα κουτί σχήματος ορθογωνίου παραλληλεπιπέδου με βάση τετράγωνο και ανοικτό από πάνω πρέπει να έχει επιφάνεια ίση με 12 dm², ποιος είναι ο μέγιστος δυνατός όγκος του;
8.	Να βρείτε το σημείο της ευθείας με εξίσωση y = 2x - 3 που είναι πλησιέστερο στην αρχή των αξόνων.
9.	Η ταχύτητα ενός κύματος μήκους λ μέσα στο νερό είναι όπου κ και c θετικές σταθερές. Για ποιο μήκος κύματος έχουμε την ελάχιστη ταχύτητα;
10.	Να προσδιοριστούν δύο θετικοί αριθμοί με τις εξής ιδιότητες: Το άθροισμά τους να είναι 10 και το άθροισμα των τετραγώνων τους να είναι ελάχιστο.

Β' ΟΜΑΔΑΣ
1.	Αν υ = 100 p(1 + ln r) - 100qr, όπου p και q θετικές σταθερές, να δείξετε ότι το υ έχει τη μέγιστη τιμή του όταν
2.	Αν όπου κ θετική σταθερά, να δείξετε ότι το υ έχει τη μέγιστη τιμή του όταν
3.	Από ένα φύλλο λαμαρίνας σχήματος τετραγώνου πλευράς 60 cm θα κατασκευαστεί ένα δοχείο, ανοικτό από πάνω, αφού κοπούν από τις γωνίες του τέσσερα ίσα τετράγωνα και στη συνέχεια διπλωθούν προς τα επάνω οι πλευρές. Να βρείτε ποιες πρέπει να είναι οι διαστάσεις του δοχείου, ώστε να έχει το μέγιστο όγκο.
4.	Θέλουμε να περιφράξουμε μια περιοχή 16000 m² σχήματος ορθογωνίου με μεταβλητές διαστάσεις και να τη χωρίσουμε στη μέση. Ο φράχτης για την περίφραξη κοστίζει 900 δρχ./m και ο φράχτης για το χώρισμα 600 δρχ./m. Να βρείτε ποιες πρέπει να είναι οι διαστάσεις του ορθογωνίου ώστε, να έχουμε το ελάχιστο κόστος για την περίφραξη μαζί με το χώρισμα.
5.	Σε έναν κύκλο ακτίνας ρ να εγγράψετε το ορθογώνιο με το μεγαλύτερο δυνατό εμβαδόν.
6.	Ένα σύρμα μήκους λ κόβεται σε δύο τμήματα με τα οποία σχηματίζουμε έναν κύκλο και ένα τετράγωνο αντιστοίχως. Να δείξετε ότι το άθροισμα των εμβαδών των δύο σχημάτων είναι ελάχιστο, όταν η πλευρά του τετραγώνου είναι ίση με τη διάμετρο του κύκλου.
7.	Η έρευνα έχει δείξει ότι αν σε έναν ασθενή γίνει μια υποδόρια ένεση, τότε ύστερα από χρόνο t η συγκέντρωση y του φαρμάκου στο αίμα του δίνεται από τη συνάρτηση όπου Α, k₁ και k₂ θετικές σταθερές με k₂ > k₁. Να βρείτε το χρόνο t στον οποίο το φάρμακο θα παρουσιάσει τη μέγιστη συγκέντρωση.
8.	Ένα ορισμένο όχημα όταν ταξιδεύει με ταχύτητα υ km/h, καταναλώνει την ώρα 6 + 0,0001υ³ λίτρα καύσιμα. i) Να βρείτε τη συνολική ποσότητα καυσίμων που χρειάζεται για να διανύσει μια απόσταση 1000km με σταθερή ταχύτητα υ. ii) Να βρείτε την τιμή του υ για την οποία έχουμε την οικονομικότερη κατανάλωση καυσίμων, καθώς και την ποσότητα καυσίμων που χρειάζεται το όχημα για να διανύσει τα 1000km. Να σχολιάσετε αν η απάντηση στο ερώτημα ii) είναι εφαρμόσιμη λόγω της μεγάλης απόστασης.
9.	Δύο ηλεκτρικές αντιστάσεις πρέπει να έχουν άθροισμα 450Ω. Πως πρέπει να επιλεγούν ώστε όταν συνδεθούν εν παραλλήλω να δίνουν τη μέγιστη ολική αντίσταση;
10.	Το μεσημέρι ένα ιστιοφόρο βρίσκεται 20 χιλιόμετρα βορείως ενός φορτηγού πλοίου. Το ιστιοφόρο ταξιδεύει νότια με 40 km/h, και το φορτηγό ανατολικά με 20 km/h. Αν η ορατότητα είναι 10 km, θα έχουν οι άνθρωποι των δύο πλοίων οπτική επαφή σε κάποια στιγμή;

ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ

1.	Αν μια συρμάτινη ράβδος είναι ομογενής, τότε η γραμμική της πυκνότητα ρ ορίζεται ως η μάζα της ανά μονάδα μήκους και μετριέται σε χιλιόγραμμα ανά μέτρο (kgr/m). Όμως αν η ράβδος δεν είναι ομογενής και η μάζα της μετρούμενη από το αριστερό άκρο της μέχρι το σημείο που απέχει από το άκρο αυτό απόσταση x μέτρα δίνεται από τη συνάρτηση m = f(x), τότε ορίζουμε ως γραμμική πυκνότητα ρ στο σημείο x το όριο δηλαδή την παράγωγο της μάζας ως προς το μήκος. Αν υποθέσουμε ότι για μια ράβδο η μάζα της δίνεται από τη συνάρτηση m = f(x) = √x, όπου το x μετριέται σε μέτρα και η μάζα της σε χιλιόγραμμα, να βρεθεί i) Η μέση πυκνότητα του τμήματος της ράβδου στο διάστημα [1, 1, 21] ii) Η γραμμική πυκνότητα της ράβδου για x = 1.
2.	Το κόστος C της ημερήσιας παραγωγής x μονάδων ενός προϊόντος από μια βιοτεχνία που απασχολεί v εργάτες δίνεται από τον τύπο: C(x) = x³ - 3vx² + 5v³ σε χιλιάδες δρχ. Το κέρδος ανά μονάδα προϊόντος είναι 16 - v χιλιάδες δρχ. Να βρείτε πόσες μονάδες πρέπει να παράγονται ημερησίως και από πόσους εργάτες, ώστε να έχουμε ελάχιστο κόστος και μέγιστο κέρδος.
3.	Σε ποιό σημείο της γραφικής παράστασης της συνάρτησης f(x) = x³ + 3x² - 2x - 1 η εφαπτομένη έχει τον ελάχιστο συντελεστή διεύθυνσης;
4.	Σε ένα ορθοκανονικό σύστημα δίνεται το σημείο A(α, β) του 1ου τεταρτημορίου. Μια ευθεία ε διέρχεται από το Α και τέμνει τους θετικούς ημιάξονες 0x και 0y στα p και q αντιστοίχως. Να δείξετε ότι η ελάχιστη τιμή του αθροίσματος p + q είναι ίση με (√α + √β)².
5.	Ποιος κύλινδρος με άθροισμα διαμέτρου και ύψους 20 cm έχει το μέγιστο δυνατό όγκο;
6.	Ένα κυλινδρικό δοχείο πρέπει να έχει χωρητικότητα 1lt. Να βρείτε τις διαστάσεις του οι οποίες ελαχιστοποιούν το κόστος του μετάλλου από το οποίο θα κατασκευαστεί το δοχείο.
7.	Από έναν κυκλικό δίσκο ακτίνας R αφαιρούμε έναν κυκλικό τομέα ΟΑΒ και ενώνοντας τις ακτίνες ΟΑ και ΟΒ κατασκευάζουμε ένα κωνικό ποτήρι. Να βρείτε τη μέγιστη χωρητικότητα του ποτηριού.
8.	Αν C(x) είναι το συνολικό κόστος για την παραγωγή x μονάδων ενός προϊόντος, τότε η συνάρτηση C λέγεται συνάρτηση κόστους, το πηλίκο λέγεται μέσο κόστος και το όριο λέγεται οριακό κόστος.

	α) Να αποδείξετε ότι αν για κάποιο x το μέσο κόστος είναι ελάχιστο, τότε ισχύει: οριακό κόστος = μέσο κόστος. β) Μια εταιρεία εκτιμά ότι το κόστος (σε δολάρια) για την παραγωγή x μονάδων ενός προϊόντος είναι i) Να βρείτε το κόστος, το μέσο κόστος και το οριακό κόστος για την παραγωγή 1000 μονάδων, 2000 μονάδων και 3000 μονάδων. ii) Ποιο είναι το επίπεδο παραγωγής για το οποίο το μέσο κόστος είναι το χαμηλότερο και ποια είναι η ελάχιστη τιμή του μέσου κόστους;
9.	Αν x μονάδες ενός προϊόντος είναι διαθέσιμες για πώληση, τότε η τιμή πώλησης p(x) της μονάδας του προϊόντος λέγεται συνάρτηση ζήτησης. Από την πώληση x μονάδων του προϊόντος, τα συνολικά έσοδα είναι R(x) = x · p(x). Η συνάρτηση R λέγεται συνάρτηση εσόδων και η παράγωγος R' λέγεται οριακή συνάρτηση εσόδων. Επίσης από την πώληση x μονάδων του προϊόντος το συνολικό κέρδος είναι P(x) = R(x) - C(x). Η συνάρτηση P καλείται συνάρτηση κέρδους και η παράγωγος P' καλείται οριακή συνάρτηση κέρδους. α) Να αποδείξετε ότι αν το κέρδος για κάποιο x είναι μέγιστο, τότε τα οριακά έσοδα είναι ίσα με το οριακό κόστος. β) Ποιο είναι το επίπεδο παραγωγής που μεγιστοποιεί τα κέρδη για μια εταιρεία, αν η συνάρτηση κόστους είναι C(x) = 3800 + 5x - 0,001x² και η συνάρτηση ζήτησης p(x) = 50 - 0,01x;
10.	Έστω υ₁ η ταχύτητα του φωτός στον αέρα και υ₂ η ταχύτητα του στο νερό. Σύμφωνα με την αρχή του Fermat, μια ακτίνα φωτός από ένα σημείο Α του αέρα φθάνει σε ένα σημείο Β του νερού ακολουθώντας μια πορεία ΑΓΒ η οποία ελαχιστοποιεί τον απαιτούμενο χρόνο. Να αποδείξετε ότι i) Ο χρόνος που χρειάζεται το φως για τη διαδρομή ΑΓΒ είναι ii) Να υπολογίσετε την t'(x). iii) Να αποδείξετε ότι

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

1.	Ο όγκος του διπλανού ορθογωνίου παραλληλεπιπέδου εκφράζεται με τη συνάρτηση V(x) = x(2 - x)(3 - x). Το πεδίο ορισμού της συνάρτησης αυτής είναι το διάστημα: Α. [0, +∞) Β. (0, 2) Γ. (-∞, 0] Δ. [2, 3].
2.	Στο διπλανό σχήμα το μήκος του τμήματος ΑΒ είναι Α. x Β. x² Γ. x² - x + 1 Δ. x - 1 - x².
3.	Το εμβαδόν του διπλανού ορθογωνίου ΑΒΓΔ είναι 63. Η τιμή του κ είναι Α. 8 Β. 2 Γ. -6 Δ. 10.
4.	Στο διπλανό σχήμα έχουμε τη γραφική παράσταση της συνάρτησης Οι τιμές του x για τις οποίες ισχύει είναι:
5.	Στο διπλανό σχήμα τα σημεία Α και Β y είναι τα σημεία τομής των καμπυλών των συναρτήσεων f(x) = ημx και Το μήκος του τμήματος ΑΒ είναι:

6.	Η γραφική παράσταση μιας συνάρτησης f φαίνεται στο διπλανό σχήμα. Το πλήθος των διακεκριμένων λύσεων της εξίσωσης (f(x))² = f(x) είναι: Α. 2 Β. 3 Γ. 4 Δ. 5 Ε. 6
7.	Στο διπλανό σχήμα έχουμε τις γραφικές παραστάσεις δυο συναρτήσεων f και g. Το άθροισμα f(2) + g(2) είναι: Α. 5 Β. 4 Γ. 3 Δ. 2
8.	Η ευθεία y = κ θέλουμε να τέμνει τη διπλανή γραφική παράσταση της συνάρτησης f σε 4 διαφορετικά σημεία. Τότε πρέπει:
9.	Με βάση τη διπλανή γραφική παράσταση της συνάρτησης f(x) = x² - 2x / A = [0, 3] να γράψετε τα ακρότατα της συνάρτησης f.
10.	Για καθένα από τα παρακάτω όρια να χρησιμοποιήσετε την αντίστοιχη γραφική παράσταση για να βρείτε την τιμή του ή να προσδιορίσετε ότι δεν υπάρχει.

11.	i) Αν f(x) = -3x² και f'(α) = 12, ποια είναι η τιμή του α; ii) Αν και ποιες τιμές μπορεί να έχει ο α; iii) Αν f(x) = ημx και ποιο είναι το σύνολο των τιμών του α;
12.	Αν για τις συναρτήσεις f και g ισχύουν f(3) = 4, g(3) = 2, f'(3) = -6 και g'(3) = 5 να βρείτε για x = 3 τις παραγώγους των συναρτήσεων
13.	Αν h(x) = f(g(x)) και g(3) = 6, g'(3) = 4 και f'(6) = 7, να βρείτε τον αριθμό h'(3) .
14.	Στην πρώτη γραμμή του παρακάτω πίνακα υπάρχουν οι γραφικές παραστάσεις μερικών συναρτήσεων και στη δεύτερη γραμμή οι παράγωγοι των συναρτήσεων αυτών. Να αντιστοιχίσετε κάθε συνάρτηση στην παράγωγό της.