| 5.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αποδοχή των μιγαδικών αριθμών, εκτός από τις δυνατότητες που άνοιξε στην επίλυση των εξισώσεων, έδωσε μεγάλη ευελιξία στον αλγεβρικό λογισμό. Για παράδειγμα, η παράσταση |
| (που σήμερα φέρει το όνομα του de Moivre), από την οποία, με χρήση του διωνυμικού αναπτύγματος, βρήκε τύπους για τα ημnz και συνnz. Όρισμα Μιγαδικού 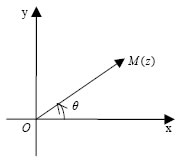 Έστω ένας μη μηδενικός μιγαδικός αριθμός z=x+yi και Ονομάζουμε όρισμα του μιγαδικού z καθεμιά από τις γωνίες που έχουν αρχική πλευρά την ημιευθεία Ox και τελική πλευρά την ημιευθεία OM . Από όλα τα ορίσματα του z ένα ακριβώς βρίσκεται στο διάστημα [0,2π) . Αυτό λέγεται πρωτεύον όρισμα του μιγαδικού z και συμβολίζεται με Arg(z) . Είναι φανερό ότι: • Tο Arg(z) είναι η γωνία που σχηματίζει η διανυσματική ακτίνα του μιγαδικού z με τον άξονα x'x . • Δύο ορίσματα του z διαφέρουν κατά γωνία 2κπ, Για το μιγαδικό z=0 δεν ορίζεται όρισμα. Γι'αυτό, στη συνέχεια, όταν αναφερόμαστε σε όρισμα μιγαδικού, θα εννοούμε ότι Τριγωνομετρική Μορφή Μιγαδικού Έστω ο μιγαδικός |
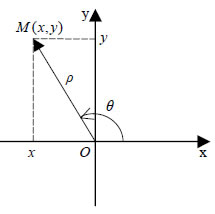 x=ρσυνθ y=ρημθ Επομένως, ο μιγαδικός z μπορεί να γραφεί ως εξής:
Ο τρόπος αυτός γραφής του μιγαδικού z λέγεται τριγωνομετρική ή πολική μορφή του z. Για παράδειγμα, αν Επομένως, μια τιμή του ορίσματος είναι η Αποδεικνύεται ότι αν λ>0 και z=λ(συνθ+iημθ) , τότε η παράσταση λ(συνθ+iημθ) είναι τριγωνομετρική μορφή του μιγαδικού αριθμού z . "Δύο μη μηδενικοί μιγαδικοί αριθμοί είναι ίσοι, αν και μόνο αν έχουν ίσα μέτρα και η διαφορά των ορισμάτων τους είναι ακέραιο πολλαπλάσιο του 2π". Δηλαδή: Αν |
| Τριγωνομετρική Μορφή Γινομένου Μιγαδικών Αν Ομοίως, για το πηλίκο τους Aποδείξαμε λοιπόν ότι: Αν
|
| Από τις τριγωνομετρικές μορφές του γινομένου και του πηλίκου μιγαδικών προκύπτουν οι ιδιότητες 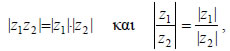 τις οποίες έχουμε συναντήσει και στην Η γεωμετρική ερμηνεία του γινομένου και του πηλίκου δύο μιγαδικών φαίνεται στα παρακάτω σχήματα:
Σύμφωνα με τα παραπάνω: • Ο πολλαπλασιασμός του μιγαδικού • Η διαίρεση του μιγαδικού z1=(συνθ1+iημθ1) με το μιγαδικό |
| Θεώρημα του De Moivre Αν z=ρ(συνθ+iημθ) είναι ένας μιγαδικός αριθμός σε τριγωνομετρική μορφή, σύμφωνα με τα προηγούμενα έχουμε: Ομοίως βρίσκουμε ότι 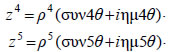 Γενικά, ισχύει το επόμενο θεώρημα: ΘΕΩΡΗΜΑ 1 Αν z=ρ(συνθ+iημθ) είναι ένας μιγαδικός αριθμός σε τριγωνομετρική μορφή και v είναι ένας θετικός ακέραιος, τότε ΑΠΟΔΕΙΞΗ Έστω Ρ(ν) η ισότητα που θέλουμε να αποδείξουμε. • Για v=1 η ισότητα γίνεται • Θα αποδείξουμε ότι αν Ρ(ν) αληθής, τότε Ρ(ν+1) αληθής, δηλαδή αν Έχουμε Άρα η Ρ(ν) αληθεύει για όλους τους θετικούς ακεραίους ν . Για παράδειγμα, αν |
| Το προηγούμενο θεώρημα αποδίδεται στο μαθηματικό De Moivre και γι'αυτό φέρει το όνομά του. Το Θεώρημα του De Moivre ισχύει και όταν ο εκθέτης είναι αρνητικός ακέραιος. Πράγματι, έχουμε 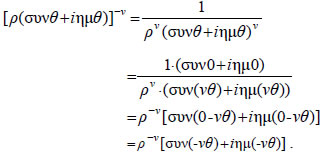 ΕΦΑΡΜΟΓΕΣ 1.Να βρεθεί το σύνολο των εικόνων των μιγαδικών z , αν ΛΥΣΗ Αν z=x+yi, τότε Άρα, 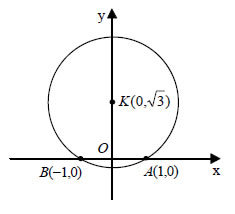 Επομένως, η συνθήκη
Άρα, το σύνολο των εικόνων του z είναι το τόξο του κύκλου κέντρου 2. Αν ημα+ημβ+ημγ=0 και συνα+συνβ+συνγ=0, να αποδειχτεί ότι ΛΥΣΗ Έστω οι μιγαδικοί a=συνα+iημα, b=συνβ+iημβ, c=συνγ+iημγ. Έχουμε και επομένως Με αντικατάσταση των και a,b και c έχουμε διαδοχικά:
Εξισώνοντας τα πραγματικά και τα φανταστικά μέρη των δύο μελών έχουμε: ΑΣΚΗΣΕΙΣ
| ||||||
| ||||||||||||||||||||
|