5.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C

Εισαγωγή

Η επίλυση των εξισώσεων 3ου και 4ου βαθμού, η "αναγκαστική" επαφή με τους μιγαδικούς αριθμούς για την έκφραση των πραγματικών ριζών και η εξέλιξη του αλγεβρικού λογισμού δημιούργησαν στις αρχές του 17ου αιώνα τις προϋποθέσεις για την ανάπτυξη μιας γενικής θεωρίας των πολυωνυμικών εξισώσεων στην Άλγεβρα. Βασικά στοιχεία αυτής της θεωρίας δεν ήταν μόνο οι μέθοδοι επίλυσης, αλλά και δομικά ζητήματα, όπως οι σχέσεις ριζών και συντελεστών μιας εξίσωσης, καθώς και η σχέση ανάμεσα στο βαθμό και στο πλήθος των ριζών. Το τελευταίο, που καθιερώθηκε αργότερα ως Θεμελιώδες Θεώρημα της Άλγεβρας

"κάθε πολυωνυμική εξίσωση ν βαθμού έχει στο σύνολο των μιγαδικών ν ακριβώς ρίζες",

διατυπώνεται στην αρχή διστακτικά, καθώς οι μιγαδικοί δε θεωρούνται ακόμη ισότιμοι προς τους υπόλοιπους αριθμούς. Ο R. Descartes, στο βιβλίο ΙΙΙ της "La Géométrie" (1637) γράφει ότι: "κάθε εξίσωση μπορεί να έχει τόσες διαφορετικές ρίζες όσες και οι διαστάσεις [δηλ. ο βαθμός] της άγνωστης ποσότητας στην εξίσωση", αλλά ονομάζει τις θετικές ρίζες "αληθινές", τις αρνητικές "ψεύτικες" και εισάγει για πρώτη φορά τον όρο "φανταστικές" για τις υπόλοιπες:

            "…ενώ μπορούμε να θεωρήσουμε ότι η εξίσωση
            έχει τρεις ρίζες, εν τούτοις υπάρχει μία μόνο πραγματική ρίζα, το 2, ενώ
            οι άλλες δύο παραμένουν φανταστικές".

Το θεμελιώδες θεώρημα της Άλγεβρας άρχισε να αποκτά εξαιρετική σημασία με την ανάπτυξη της Ανάλυσης, καθώς η παραγοντοποίηση των πολυωνύμων έπαιζε πρωταρχικό ρόλο στον υπολογισμό ολοκληρωμάτων (διάσπαση ρητών κλασμάτων σε απλά κλάσματα). Ο G.W. Leibniz έθεσε το 1702 αυτό το ζήτημα ισχυριζόμενος (λαθεμένα) ότι το πολυώνυμο δεν αναλύεται σε γινόμενο παραγόντων 1ου ή 2ου βαθμού με πραγματικούς συντελεστές. Το γεγονός αυτό οδήγησε στις πρώτες συστηματικές προσπάθειες να αποδειχτεί ότι κάθε πολυώνυμο με πραγματικούς συντελεστές αναλύεται σε γινόμενο παραγόντων 1ου ή 2ου βαθμού, που αποτελεί μια άλλη ισοδύναμη μορφή του θεμελιώδους θεωρήματος. Ύστερα από ορισμένες ημιτελείς προσπάθειες των d'Alembert (1746), L. Euler (1749) και J.L. Lagrange (1772), ο C.F. Gauss έδωσε την πρώτη αυστηρή απόδειξη το 1799 (σε ηλικία 22 χρονών), στη

στη διδακτορική του διατριβή που είχε τίτλο: "Νέα απόδειξη του θεωρήματος ότι κάθε ακέραια ρητή συνάρτηση μιας μεταβλητής μπορεί να αναλυθεί σε πραγματικούς παράγοντες πρώτου και δεύτερου βαθμού".

Η Eξίσωση z^ν=1

Γνωρίζουμε ότι στο σύνολο των πραγματικών αριθμών η εξίσωση z^ν=1 έχει μια λύση, την z=1, αν ο ν είναι περιττός και δύο λύσεις, τις z₁=1 και z₂=-1, αν ο ν είναι άρτιος.

Ας λύσουμε τώρα στο σύνολο C των μιγαδικών αριθμών μερικές εξισώσεις της μορφής z^ν=1, όπου ν θετικός ακέραιος. Έχουμε:

Εικόνα

δηλαδή η εξίσωση έχει στο C τρεις ρίζες.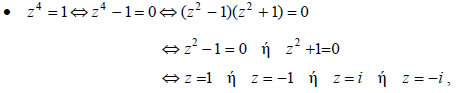

δηλαδή η εξίσωση έχει στο σύνολο C τέσσερις λύσεις.

Γενικά ισχύει το επόμενο θεώρημα:

ΘΕΩΡΗΜΑ 2

Στο σύνολο των μιγαδικών αριθμών η εξίσωση z^ν=1 , όπου ν θετικός ακέραιος, έχει ν ακριβώς διαφορετικές λύσεις, οι οποίες δίνονται από τον τύπο:

ΑΠΟΔΕΙΞΗ

Έστω r(συνθ+iημθ) μια λύση σε τριγωνομετρική μορφή της εξίσωσης z^ν=1 .

Τότε,

οπότε

Άρα, r^ν=1 και νθ-0=2κπ, ,δηλαδή r=1 και , . Επομένως, οι λύσεις της εξίσωσης z^ν=1 , θα είναι της μορφής

Αλλά και αντιστρόφως, κάθε μιγαδικός της μορφής , είναι λύση της εξίσωσης z^ν=1, αφού

Άρα, οι λύσεις της εξίσωσης z^ν=1 είναι οι αριθμοί

Για κ=0 έχουμε την προφανή λύση της εξίσωσης z₀=1 , την οποία βρίσκουμε
και για κ=ν, αφού .

Αν θέσουμε , τότε για τις ρίζες της z^ν=1 , θα ισχύει η σχέση

Είναι λοιπόν: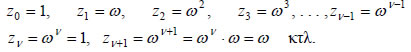

Παρατηρούμε λοιπόν ότι οι λύσεις της z^ν=1 που δίνονται από την (1) δεν είναι όλες διαφορετικές μεταξύ τους. Θα εξετάσουμε για ποιες τιμές του κ έχουμε διαφορετικές λύσεις. Επειδή για κάθε υπάρχουν ακέραιοι ρ και υ, τέτοιοι, ώστε να είναι , θα έχουμε:

Δηλαδή, για κάθε η λύση z_κ ταυτίζεται με μια από τις

Θα δείξουμε τώρα ότι οι λύσεις 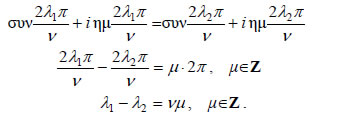είναι διαφορετικές μεταξύ τους. Έστω ότι δε συμβαίνει αυτό. Τότε θα υπάρχουν φυσικοί λ₁ λ₁ με , τέτοιοι, ώστε , οπότε θα έχουμε διαδοχικά:

Από την τελευταία ισότητα προκύπτει ότι ο ακέραιος ν διαιρεί τη διαφορά λ₁-λ₂. Αυτό όμως είναι άτοπο, αφού .
Επομένως, οι λύσεις της εξίσωσης z^ν=1 είναι οι ν διαφορετικοί αριθμοί

όπου

Οι λύσεις αυτές λέγονται και νιοστές ρίζες της μονάδας.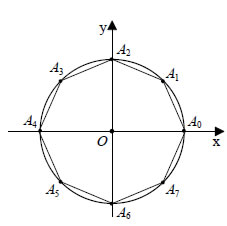

Οι εικόνες των αντίστοιχων λύσεων της εξίσωσης z^ν=1 είναι κορυφές κανονικού πολυγώνου με ν πλευρές εγγεγραμμένου σε κύκλο με κέντρο O(0,0) και ακτίνα r=1. Πιο συγκεκριμένα:

- Η κορυφή A₀ παριστάνει τη λύση 1.
- Η επόμενη κορυφή A₁ παριστάνει τη λύση .
- Η κορυφή A₂ παριστάνει την ω² και προκύπτει από την ω με στροφή του διανύσματος κατά γωνία .

H κορυφή A₃ παριστάνει την ω³ και προκύπτει από την ω με στροφή του διανύσματος κατά γωνία κτλ.

Η Eξίσωση z^ν=a,

Έστω μια τριγωνομετρική μορφή του μιγαδικού a. Τότε από τον τύπο του de Moivre έχουμε: Εικόνα

Αν θέσουμε Εικόνα τότε η εξίσωση z^ν=a γράφεται
ή ισοδύναμα

Eπομένως, το μπορεί να πάρει τις ν διαφορετικές τιμές

οπότε οι λύσεις της εξίσωσης z^ν=a είναι οι αριθμοί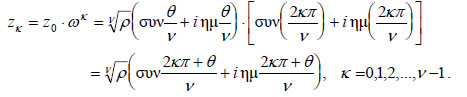

Αποδείξαμε λοιπόν ότι:

Στο σύνολο των μιγαδικών αριθμών η εξίσωση z^ν=a , όπου ν θετικός ακέραιος και a=ρ(συνθ+iημθ), ρ>0, έχει ν διαφορετικές λύσεις οι οποίες δίνονται από τον τύπο:

Οι εικόνες των λύσεων της εξίσωσης z^ν=a στο μιγαδικό επίπεδο είναι κορυφές κανονικού πολυγώνου με ν πλευρές εγγεγραμμένου σε κύκλο με κέντρο O(0,0) και ακτίνα , όπου .

Έστω για παράδειγμα η εξίσωση

Επειδή , οι λύσεις z_κ της εξίσωσης (1) δίνονται
από τον τύπο Εικόνα

Πιο συγκεκριμένα οι λύσεις είναι: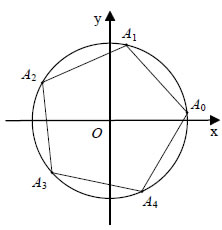

Εικόνα

Οι λύσεις αυτές είναι κορυφές κανονικού πενταγώνου εγγεγραμμένου σε κύκλο
ακτίνας ρ=2

Πολυωνυμικές Εξισώσεις με Πραγματικούς Συντελεστές

Όπως αναφέρθηκε στην εισαγωγή, κάθε πολυωνυμική εξίσωση P(z), νιοστού βαθμού, δηλαδή κάθε εξίσωση της μορφής

έχει στο σύνολο των μιγαδικών αριθμών ν ακριβώς ρίζες.

Αν είναι οι ρίζες του πολυωνύμου P(z) (οι οποίες δεν είναι κατανάγκη διαφορετικές), τότε αποδεικνύεται ότι το πολυώνυμο αναλύεται σε

γινόμενο παραγόντων ως εξής:

Επομένως, η επίλυση πολυωνυμικών εξισώσεων στο C γίνεται με τις ίδιες μεθόδους που χρησιμοποιούνται και στο σύνολο R των πραγματικών αριθμών. Στη συνέχεια θα περιοριστούμε σε πολυωνυμικές εξισώσεις με πραγματικούς μόνο συντελεστές.
Έχουμε ήδη λύσει τη δευτεροβάθμια εξίσωση, η οποία, όπως είδαμε, έχει δύο ρίζες, οι οποίες, αν δεν είναι πραγματικές, είναι μιγαδικές συζυγείς. Ας λύσουμε τώρα μία ανωτέρου βαθμού, για παράδειγμα την , που είναι πολυωνυμική τρίτου βαθμού. Έχουμε:

Όμως,

Άρα, οι ρίζες της εξίσωσης είναι , και 1. Και στην περίπτωση αυτή παρατηρούμε ότι οι μιγαδικές ρίζες της εξίσωσης είναι συζυγείς. Το συμπέρασμα αυτό γενικεύεται για οποιαδήποτε πολυωνυμική εξίσωση με πραγματικούς συντελεστές.

ΘΕΩΡΗΜΑ 3

Αν ο μιγαδικός αριθμός z₀=α+βi είναι ρίζα μιας πολυωνυμικής εξίσωσης με πραγματικούς συντελεστές, τότε και ο συζυγής του είναι ρίζα της εξίσωσης αυτής.

ΑΠΟΔΕΙΞΗ

Μια πολυωνυμική εξίσωση, όπως γνωρίζουμε, έχει τη μορφή:

Αφού ο αριθμός z₀ είναι η ρίζα της εξίσωσης, έχουμε κατά σειρά: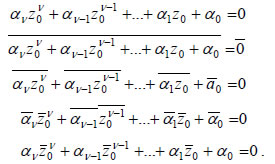

Άρα, ο είναι και αυτός ρίζα της εξίσωσης.

ΕΦΑΡΜΟΓΕΣ

1.Aν να αποδειχτεί ότι:

ΑΠΟΔΕΙΞΗ

Εικόνα

2.Να λυθεί η εξίσωση . Αν x₁ x₁, είναι οι ρίζες της εξίσωσης αυτής, να κατασκευαστεί εξίσωση 2ου βαθμού που να έχει ρίζες τις

ΛΥΣΗ

Έχουμε

Eπομένως,

Η ζητούμενη εξίσωση θα είναι η

Έχουμε

και

Εικόνα

Επομένως:

Εικόνα

Άρα, η ζητούμενη εξίσωση είναι η:

3. Να αναλυθεί σε γινόμενο πολυωνύμων το πολυώνυμο , αν γνωρίζουμε ότι έχει ρίζα το μιγαδικό αριθμό .

ΛΥΣΗ

Αφού το P(x) έχει ρίζα τον , θα έχει ρίζα και το συζυγή του . Επομένως, το πολυώνυμο P(x) διαιρείται με το γινόμενο , για το οποίο έχουμε

Εικόνα

Αν κάνουμε τη διαίρεση P(x):Q(x), βρίσκουμε πηλίκο 3x+2, επομένως είναι .

ΣΧΟΛΙΟ

Γενικά, όπως αναφέρθηκε και στην εισαγωγή: κάθε πολυώνυμο με πραγματικούς συντελεστές μπορεί να γραφεί ως γινόμενο πρωτοβάθμιων και δευτεροβάθμιων παραγόντων με πραγματικούς συντελεστές, όπου οι δευτεροβάθμιοι παράγοντες (αν υπάρχουν) έχουν αρνητική διακρίνουσα.

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ

Να λύσετε τις εξισώσεις και να παραστήσετε τις λύσεις στο μιγαδικό επίπεδο:

α) z³=1 β) z⁴=1 γ) z⁶=1.

2.	Να λύσετε τις εξισώσεις:
3.	Να λύσετε τις εξισώσεις:
4.	Να λύσετε τις εξισώσεις: α) z³+3z²+4z=8 β) z⁴+5z²+4=0
5.	Αν ο μιγαδικός 2+i είναι ρίζα της εξίσωσης 3x³-10x²+7x+10=0, να βρείτε και τις άλλες ρίζες της.
6.	Αν w είναι μια κυβική ρίζα της μονάδος, με , να βρείτε την τιμή της παράστασης (1-w+w²)(1+w-w²)
7.	7. Να λύσετε την εξίσωση 1+x+x²+x³+x⁴+x⁵=0 .
8.	8. Να λύσετε την εξίσωση z³+3z²+3z+9=0 και να δείξετε ότι οι εικόνες των ριζών είναι κορυφές ισόπλευρου τριγώνου.

Β' ΟΜΑΔΑΣ
1.	Να λύσετε τις εξισώσεις: α) z³=1-i β) (z-1)³-(1-i)(z+1)³=0.
2.	Να λύσετε την εξίσωση z⁶+2z⁵+2z⁴+2z³+z²+(z+1)²=0
3.	Να λύσετε την εξίσωση z⁷+1=0 και στη συνέχεια να βρείτε τα τριώνυμα με πραγματικούς συντελεστές που είναι παράγοντες του πολυωνύμου z⁶-z⁵+z⁴-z³+z²-z+1.
4.	Στο σύνολο των μιγαδικών αριθμών να βρείτε τις κοινές λύσεις των εξισώσεων (z²+1)²+z³+z=0 και z¹⁶+2z¹⁴+1=0.
5.	Να βρείτε τους μιγαδικούς αριθμούς z , για τους οποίους ισχύει


6.	Αν η εξίσωση (1+iz)^ν=p(1-iz)^ν, έχει πραγματική ρίζα, να αποδείξετε ότι
7.	Δίνεται η εξίσωση x²-2x+4=0 με ρίζες τις x₁ και x₂ . α) Να υπολογίσετε τις τιμές των παραστάσεων x₁+x₂, x₁x₂ και . β) Αν η εξίσωση x²+px+q=0 έχει ως ρίζες τις, να βρείτε τις τιμές των p και q.
8.	α) Να λύσετε την εξίσωση β) Να αποδείξετε ότι καθώς το θ μεταβάλλεται στο διάστημα οι εικόνες των λύσεων της εξίσωσης κινούνται σε μια υπερβολή.
9.	Να λύσετε την εξίσωση x⁹-x⁵+x⁴-1=0.

ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ

1.	Δίνεται η συνάρτηση με . α) Να αποδείξετε ότι β) Να βρείτε το είδος της καμπύλης στην οποία ανήκουν τα σημεία M(x,y), για τα οποία οι μιγαδικοί αριθμοί z=αx+βyi με α,β,x,y ικανοποιούν τη σχέση (α, β σταθερά).
2.	Θεωρούμε τους μιγαδικούς z,w και w₁, για τους οποίους ισχύουν: w=z-zi και , όπου . Να δείξετε ότι αν το α μεταβάλλεται στο R^* και ισχύει , τότε η εικόνα P του z στο μιγαδικό επίπεδο κινείται σε μια υπερβολή.
3.	Θεωρούμε τους μιγαδικούς z=λ+2+(3λ-1)i, α) Να βρείτε το γεωμετρικό τόπο των εικόνων του μιγαδικού z

	β) Να βρείτε το γεωμετρικό τόπο των εικόνων του μιγαδικού w για τον οποίο ισχύει w=z+(1+i) γ) Να βρείτε το μιγαδικό z που έχει την πλησιέστερη εικόνα στην αρχή O(0,0).
4.	Να γραμμοσκιάσετε το τμήμα του μιγαδικού επιπέδου που ορίζουν οι εικόνες των μιγαδικών z, για τους οποίους ισχύει: α) β)
5.	Να αποδείξετε ότι αν οι μιγαδικοί z₁,z₂,....,z_κ έχουν τις εικόνες τους στο ίδιο ημιεπίπεδο μιας ευθείας που διέρχεται από την αρχή O(0,0), τότε ισχύει
6.	Να αποδείξετε ότι οι εικόνες των λύσεων της εξίσωσης (1-z)^ν=z^ν είναι σημεία της ευθείας
7.	Αν το τριώνυμο αx²+βx+γ με πραγματικούς συντελεστές και δεν έχει πραγματικές ρίζες, να αποδείξετε ότι: α) Για οποιουσδήποτε πραγματικούς αριθμούς κ και λ ισχύει β) Για οποιουσδήποτε συζυγείς μιγαδικούς z₁ και z₂ διαφορετικούς από τις ρίζες του τριωνύμου ισχύει επίσης
8.	Γνωρίζοντας ότι για τις νιοστές ρίζες της μονάδας 1,z₁,z₂,....,z_κ ισχύει 1+z₁+z₂+....+z_ν-1=0 , να αποδείξετε τις ταυτότητες: α) β)

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

1.	Να βάλετε σε κύκλο τη σωστή απάντηση: (i) Αν στο σύνολο των μιγαδικών αριθμών ισχύει u²+ν²=0, τότε : Α. u=0 Β. ν=0 Γ. u=ν=0 Δ. Τίποτα από τα προηγούμενα.

	(ii) Ο αριθμός είναι: Α. Φανταστικός Β. Μηδέν Γ. Πραγματικός Δ. Τίποτα από τα προηγούμενα.
2.	Ποιες από τις επόμενες ισότητες αληθεύουν για κάθε μιγαδικό z :
3.	Σύμφωνα με τη συνθήκη που ικανοποιούν οι μιγαδικοί z και αναφέρεται στην πρώτη στήλη, να τους αντιστοιχίσετε στην ευθεία της δεύτερη στήλης που ανήκει η εικόνα τους:
4.	Να αντιστοιχίσετε κάθε μιγαδικό z της πρώτης στήλης στο όρισμά του της δεύτερης στήλης:
5.	Να βάλετε σε κύκλο τις σωστές απαντήσεις. Ό αριθμός των μιγαδικών ριζών μιας πολυωνυμικής εξίσωσης 5ου βαθμού με πραγματικούς συντελεστές μπορεί να είναι:

Α.1 Β.2 Γ.3 Δ.4 Ε.5

Να γράψετε τους μιγαδικούς που έχουν ως εικόνες τα σημεία Α, Β, Γ και Δ του διπλανού σχήματος:

                   A:
                   Β:
                   Γ:
                   Δ:

Αν z είναι ο μιγαδικός που έχει ως εικόνα το Α, να αντιστοιχίσετε κάθε μιγαδικό της πρώτης στήλης στην εικόνα του που αναφέρεται στη δεύτερη στήλη και σημειώνεται στο διπλανό σχήμα:

Εικόνα