5.3 ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ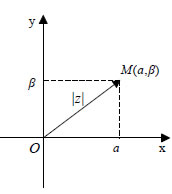

Έστω Μ(α,β)η εικόνα του μιγαδικού z=α+βi στο μιγαδικό επίπεδο. Ορίζουμε ως μέτρο του z την απόσταση του M από την αρχή O , δηλαδή

Εικόνα

Για παράδειγμα,

Όταν ο μιγαδικός z είναι της μορφής , τότε , που είναι η γνωστή μας απόλυτη τιμή του πραγματικού αριθμού α.

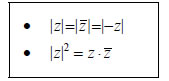Οι επόμενες ιδιότητες αναφέρονται στις σχέσεις που συνδέουν το γινόμενο και το πηλίκο μιγαδικών με τα μέτρα τους και είναι ίδιες με τις αντίστοιχες ιδιότητες των απόλυτων τιμών πραγματικών αριθμών.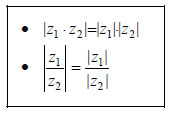
Αν z₁,z₂ είναι μιγαδικοί αριθμοί, τότε

Πράγματι έχουμε:

Εικόνα

Ανάλογα αποδεικνύεται και η δεύτερη ιδιότητα.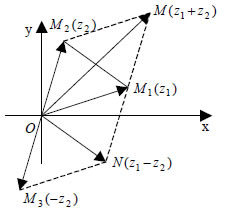
Γενικά, αποδεικνύεται ότι

Τέλος, από τη γνωστή μας τριγωνική ανισότητα και από τη γεωμετρική ερμηνεία του αθροίσματος z₁+z₂ και της διαφοράς z₁-z₂ δύο μιγαδικών προκύπτει ότι:

Επίσης, είναι φανερό ότι το μέτρο του διανύσματος είναι ίσο με το μέτρο του διανύσματος . Επομένως:

"Το μέτρο της διαφοράς δύο μιγαδικών είναι ίσο με την απόσταση των εικόνων τους".

Δηλαδή: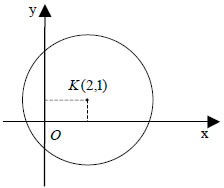

Έτσι, για παράδειγμα, η εξίσωση επαληθεύεται από όλους τους μιγαδικούς z που έχουν την ιδιότητα οι εικόνες τους να απέχουν από την εικόνα του μιγαδικού 2+i , δηλαδή από το σημείο K(2,1) του μιγαδικού επιπέδου, απόσταση 3 μονάδες και μόνο από αυτούς. Επομένως, η εξίσωση αυτή είναι εξίσωση κύκλου με κέντρο το σημείο K(2,1) και ακτίνα ρ=3.
Γενικά, η εξίσωση

παριστάνει τον κύκλο με κέντρο το σημείο K(z₀) και ακτίνα ρ.

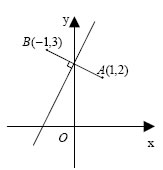Επίσης η εξίσωση επαληθεύεται από όλους τους μιγαδικούς z που έχουν την ιδιότητα οι εικόνες τους να ισαπέχουν από τις εικόνες των μιγαδικών 1+2i και -1+3i, δηλαδή από τα σημεία A(1,2)και B(-1,3) , και μόνο από αυτούς. Επομένως, η εξίσωση αυτή είναι εξίσωση της μεσοκαθέτου του τμήματος AB.

Γενικά, η εξίσωση

παριστάνει τη μεσοκάθετο του τμήματος με άκρα τα σημεία A(z₁) και B(z₂) .

ΕΦΑΡΜΟΓΕΣ

1.Αν για τους μιγαδικούς ισχύει

να αποδειχτεί ότι κανένας από αυτούς δεν είναι πραγματικός αριθμός.

ΑΠΟΔΕΙΞΗ

Αν ένας από τους 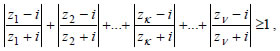για παράδειγμα ο z_κ, ήταν πραγματικός, τότε οι μιγαδικοί z_κ-i και z_κ+i θα ήταν συζυγείς και επομένως Εικόνα

αφού
τα μέτρα δύο συζυγών μιγαδικών είναι ίσα. Τότε όμως θα είχαμε

που είναι άτοπο.

2. Αν για το μιγαδικό z ισχύει , να βρεθεί:
α) Ο γεωμετρικός τόπος της εικόνας του z στο μιγαδικό επίπεδο.
β) Η μέγιστη και η ελάχιστη τιμή του .

ΛΥΣΗ

α) Η ισότητα επαληθεύεται από όλους τους μιγαδικούς z που έχουν την ιδιότητα οι εικόνες τους να απέχουν από το σημείο K(2,2) σταθερή απόσταση ίση

ίση με και μόνο από αυτούς. Επομένως, ο ζητούμενος γεωμετρικός τόπος είναι ο κύκλος με κέντρο K(2,2) και ακτίνα δηλαδή ο κύκλος

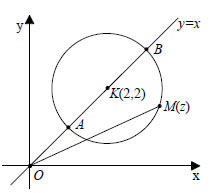β) Το είναι η απόσταση της εικόνας M(z) από την αρχή O(0,0), δηλαδή (OM)το μήκος. Από τη Γεωμετρία, όμως, γνωρίζουμε ότι αν η ευθεία OΚ τέμνει τον κύκλο στα A και B, τότε , που σημαίνει ότι η μέγιστη τιμή του είναι το μήκος (OB) και η ελάχιστη το μήκος .
Η εξίσωση, όμως, της ευθείας OΚ είναι η y=x . Επομένως, οι συντεταγμένες των σημείων A καιB θα είναι οι λύσεις του συστήματος

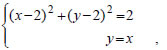που είναι τα ζεύγη (1,1) και (3,3). Άρα, η μέγιστη τιμή του είναι ίση με και η ελάχιστη ίση με

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ
1.	Να βρείτε τα μέτρα των μιγαδικών αριθμών: 1+i, 1-i, 3+4i, 3-4i -5i, -4,
2.	Να βρείτε τα μέτρα των μιγαδικών αριθμών: όπου
3.	Να βρείτε τους μιγαδικούς z=x+yi για τους οποίους ισχύει:
4.	Να βρείτε που ανήκουν οι μιγαδικοί z για τους οποίους ισχύει:

5.	Να βρείτε που ανήκουν οι εικόνες των μιγαδικών z για τους οποίους ισχύει:
6.	Αν , να βρείτε το γεωμετρικό τόπο της εικόνας του μιγαδικού z, όπου
7.	Από τους μιγαδικούς z, για τους οποίους ισχύει , ποιος έχει το ελάχιστο και ποιος το μέγιστο δυνατό μέτρο;
8.	Αν για τους μιγαδικούς z ισχύει , να βρείτε που ανήκουν οι εικόνες των μιγαδικών w με .
9.	Για δύο μιγαδικούς αριθμούς z₁ και z₂ να αποδείξετε ότι

Β' ΟΜΑΔΑΣ
1.	Να δείξετε ότι για κάθε μιγαδικό z ισχύει:
2.	Έστω ο μιγαδικός z , για τον οποίο ισχύει . Να αποδείξετε ότι: Αν , τότε ο είναι φανταστικός αριθμός και αντιστρόφως.
3.	Έστω ο μιγαδικός z με . Να αποδείξετε ότι: Ο είναι πραγματικός, αν και μόνο αν ο z είναι πραγματικός ή
4.	Έστω ο μιγαδικός z με όπου . Να αποδείξετε ότι: ο είναι φανταστικός, αν και μόνο αν ο z είναι φανταστικός.
5.	Αν η εικόνα του μιγαδικού z ανήκει στον κύκλο O(0,0) και ακτίνας ρ=1, να δείξετε ότι το ίδιο ισχύει και για την εικόνα του μιγαδικού .
6.	6. Αν για το μιγαδικό z ισχύει, να δείξετε ότι η εικόνα του z ανήκει στον κύκλο με κέντρο O(0,0) και ακτίνα ρ=1 .
7.	Αν για το μιγαδικό z ισχύει , να βρείτε την τιμή της παράστασης . Να ερμηνεύσετε γεωμετρικά το συμπέρασμα.

8.	Να βρείτε το γεωμετρικό τόπο των εικόνων Μ των μιγαδικών z, για τους οποίους ισχύει: Ποιο από τα σημεία Μ απέχει την ελάχιστη απόσταση από την αρχή O(0,0).
9.	Αν M₁ και M₂ είναι οι εικόνες των μιγαδικών z₁ και z₂ αντιστοίχως και , να αποδείξετε ότι: Όταν το M₁ κινείται σε κύκλο κέντρου O(0,0) και ακτίνας 4, τότε το M₂ κινείται σε μια έλλειψη.
10.	α) Αν , να δείξετε ότι β) Αν για τους μιγαδικούς z₁,z₂,......z_κ ισχύει να αποδείξετε ότι: