5.2 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ

Σύμφωνα με τον ορισμό του C, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικών αριθμών γίνονται όπως ακριβώς και οι αντίστοιχες πράξεις με διώνυμα α+βx στο R, όπου βέβαια αντί για x έχουμε το i. Έτσι:
• Για την πρόσθεση δύο μιγαδικών αριθμών α+βi και γ+δi έχουμε:

• Για την αφαίρεση του μιγαδικού αριθμού γ+δi από τον α+βi, επειδή ο αντίθετος του μιγαδικού γ+δi είναι ο μιγαδικός -γ-δi, έχουμε:

Δηλαδή

Για παράδειγμα                               (3+4i)-(5-6i)=(3-5+(4+6)i=-2+10i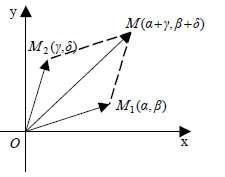

Αν M₁(α,β) και M₂(γ,δ) είναι οι εικόνες των α+βi και γ+δi αντιστοίχως στο μιγαδικό επίπεδο, τότε το άθροισμα

παριστάνεται με το σημείο M(α+γ,β+δ).

Επομένως, ισχύει , δηλαδή:

"Η διανυσματική ακτίνα του αθροίσματος των μιγαδικών α+βi και γ+δi είναι το άθροισμα των διανυσματικών ακτίνων τους".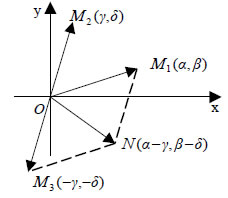

Επίσης, η διαφορά

       (α+βi)-(γ+δi)=(α-γ)+(β-δ)i

παριστάνεται με το σημείο

                    N(α-γ, β-δ).

Επομένως,ισχύει

δηλαδή:

"Η διανυσματική ακτίνα της διαφοράς των μιγαδικών α+βi και γ+δi είναι η διαφορά των διανυσματικών ακτίνων τους".

• Για τον πολλαπλασιασμό δύο μιγαδικών α+βi και γ+δi έχουμε:

Δηλαδή,

Για παράδειγμα,

Ειδικότερα, έχουμε: . Ο αριθμός α-βi λέγεται συζυγής του α+βi και συμβολίζεται με . Δηλαδή,

Επειδή είναι και λέγονται συζυγείς μιγαδικοί.

• Τέλος, για να εκφράσουμε το πηλίκο , όπου , στη μορφή κ+λi , πολλαπλασιάζουμε τους όρους του κλάσματος με το συζυγή του παρονομαστή και έχουμε:

Για παράδειγμα:

Δύναμη Μιγαδικού

Οι δυνάμεις ενός μιγαδικού αριθμού z με εκθέτη ακέραιο ορίζονται ακριβώς όπως και στους πραγματικούς, δηλαδή ορίζουμε:

για κάθε θετικο ακέραιο ν , με ν>1 . Επίσης, αν , ορίζουμε

για καθε θετικό ακέραιο ν.

Για τις δυνάμεις των μιγαδικών αριθμών ισχύουν οι ίδιες ιδιότητες που ισχύουν και για τις δυνάμεις των πραγματικών αριθμών. Ιδιαίτερα για τις δυνάμεις του i έχουμε:

Στη συνέχεια παρατηρούμε ότι είναι:

δηλαδή, μετά το i⁴ οι τιμές του i^v επαναλαμβάνονται. Άρα, για να υπολογίσουμε συγκεκριμένη δύναμη του i, γράφουμε τον εκθέτη v στη μορφή ν=4ρ+υ, όπου ρ το πηλίκο και υ το υπόλοιπο της ευκλείδειας διαίρεσης του ν με το 4, οπότε έχουμε:

Ιδιότητες Συζυγών

Επειδή οι συζυγείς μιγαδικοί, όπως θα δούμε στις επόμενες παραγράφους, μας διευκολύνουν στη μελέτη των μιγαδικών αριθμών, θα αναφερθούμε ιδιαιτέρως σε αυτούς.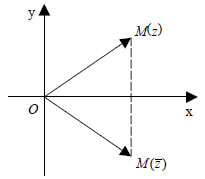

• Στο μιγαδικό επίπεδο οι εικόνες M(α,β) και M΄(α,-β) δύο συζυγών μιγαδικών z=α+βi και είναι σημεία συμμετρικά ως προς τον πραγματικό άξονα.

• Για δύο συζυγείς μιγαδικούς αριθμούς z=α+βi και μπορούμε εύκολα, με εκτέλεση των πράξεων, να διαπιστώσουμε ότι:

• Αν z₁=α+βi και z₂=γ+δi είναι δυο μιγαδικοί αριθμοί, τότε: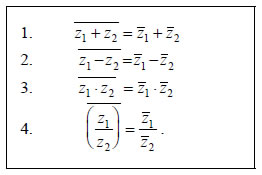

Οι ιδιότητες αυτές μπορούν να αποδειχτούν με εκτέλεση των πράξεων. Για παράδειγμα έχουμε:

C

Οι παραπάνω ιδιότητες ισχύουν και για περισσότερους από δυο μιγαδικούς αριθμούς. Είναι δηλαδή: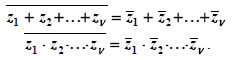

Ιδιαίτερα, αν είναι z₁=z₁=...=z_ν=z, τότε η τελευταία ισότητα γίνεται:

Επίλυση της Εξίσωσης

Επειδή , η εξίσωση z²=-1 έχει στο σύνολο C των μιγαδικών αριθμών δύο λύσεις, τις z₁=i και z₂=-i. Ομοίως, η εξίσωση z²=-4 έχει στο σύνολο των μιγαδικών αριθμών δύο λύσεις, τις z₁=2i και z₂=-2i, αφού

Εύκολα όμως μπορούμε να διαπιστώσουμε ότι και κάθε εξίσωση δεύτερου βαθμού με πραγματικούς συντελεστές έχει πάντα λύση στο σύνολο C. Πράγματι, έστω η εξίσωση

Εργαζόμαστε όπως στην αντίστοιχη περίπτωση στο R και τη μετασχηματίζουμε, με τη μέθοδο συμπλήρωσης τετραγώνων, στη μορφή: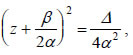

όπου η διακρίνουσα της εξίσωσης. Έτσι, έχουμε τις εξής περιπτώσεις:

• Δ>0. Tότε η εξίσωση έχει δύο πραγματικές λύσεις:

• Δ=0. Tότε έχει μια διπλή πραγματική λύση:

• Δ>0. Tότε, επειδή η εξίσωση

γράφεται:

Άρα οι λύσεις της είναι:

οι οποίες είναι συζυγείς μιγαδικοί αριθμοί.

Για παράδειγμα, η εξίσωση z²-5z+6=0 έχει Δ=25-24=1>0 και οι λύσεις της είναι:

Όμως, η εξίσωση z²-2z+2=0 έχει Δ=4-8=-4<0 και οι λύσεις της είναι οι συζυγείς μιγαδικοί αριθμοί:

ΠΑΡΑΤΗΡΗΣΗ

Παρατηρούμε ότι και εδώ ισχύουν οι σχέσεις:

ΕΦΑΡΜΟΓΕΣ

1. Για τις διάφορες τιμές του θετικού ακέραιου ν να υπολογιστεί το άθροισμα

ΛΥΣΗ

Οι προσθετέοι του αθροίσματος έχουν πλήθος ν και είναι διαδοχικοί όροι γεωμετρικής προόδου με πρώτο όρο i και λόγο επίσης i . Επομένως, , οπότε, λόγω της ισότητας ν=4ρ+υ της ευκλείδειας διαίρεσης του ν με το 4, έχουμε τις εξής περιπτώσεις:

• υ=0. Τότε ν=4ρ, οπότε .

• υ=1. Τότε ν=4ρ+1, οπότε

• υ=2. Τότε ν=4ρ+2, οπότε

• υ=3. Τότε ν=4ρ+3, οπότε

2. Να βρεθεί το σύνολο των εικόνων των μιγαδικών z στις περιπτώσεις κατά τις οποίες ο αριθμός είναι α) φανταστικός β) πραγματικός.

ΛΥΣΗ

Αν z=x+yi, τότε           

Επομένως:

α) Ο αριθμός είναι φανταστικός, αν και μόνο αν , δηλαδή, αν και μόνο αν ή ισοδύναμα

και .

Άρα, το σύνολο των εικόνων του z είναι τα σημεία της ευθείας με εξίσωση 2x+y-2=0, με εξαίρεση το σημείο A(0,2).

Ασκήσεις