4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ

Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του 22 με τον 5. Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος, ώστε:

Για να βρούμε, λοιπόν, το κ, σχηματίζουμε τις διαφορές: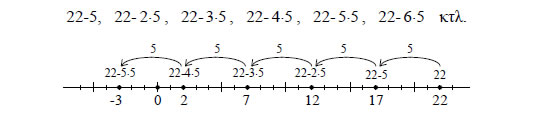

Παρατηρούμε ότι αφού οι αριθμοί αυτοί συνεχώς μειώνονται, από ένα σημείο και μετά θα είναι όλοι αρνητικοί. Ο μικρότερος μη αρνητικός ακέραιος από τους παραπάνω αριθμούς, ο οποίος είναι μικρότερος του 5, είναι ο 22 − 4∙5 = 2. Συμπεραίνουμε, λοιπόν, ότι το πηλίκο της διαίρεσης του 22 με τον 5 είναι 4 και το υπόλοιπο 2 και έχουμε:

Γενικά, ισχύει:

ΘΕΩΡΗΜΑ 1

Αν α και β είναι φυσικοί αριθμοί με , τότε υπάρχουν μοναδικοί φυσικοί κ και υ , τέτοιοι, ώστε
                                                           

ΑΠΟΔΕΙΞΗ

• Θεωρούμε τους ακέραιους α, α- β, α -2β, α -3β,... και από αυτούς παίρνουμε τους μη αρνητικούς. Σχηματίζουμε δηλαδή το σύνολο

Το σύνολο αυτό είναι υποσύνολο του N και επιπλέον είναι διάφορο του κενού, αφού περιέχει τον . Αν υ είναι το ελάχιστο στοιχείο ¹ του S , τότε θα υπάρχει , τέτοιος, ώστε υ=α- κβ , οπότε θα ισχύει

Για τον υ πρέπει να δείξουμε ότι είναι και μικρότερος του β . Ας υποθέσουμε λοιπόν ότι . Τότε

Άρα, ο υ -β είναι στοιχείο του συνόλου S , του οποίου ελάχιστο στοιχείο είναι το υ . Έτσι θα ισχύει , που είναι άτοπο. Επομένως, .

• Μένει τώρα να αποδείξουμε ότι οι φυσικοί αριθμοί κ και υ είναι μοναδικοί. Ας υποθέσουμε ότι και οι φυσικοί κ' και υ' έχουν την ιδιότητα

Επειδή οπότε

¹ Αποδεικνύεται ότι κάθε μη κενό υποσύνολο των φυσικών αριθμών έχει ελάχιστο στοιχείο ("αρχή της καλής διάταξης")

Όμως, 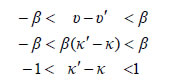. Επομένως, με πρόσθεση κατά μέλη έχουμε:

Αλλά ο μοναδικός ακέραιος μεταξύ -1 και 1 είναι το 0. Άρα κ' - κ =0 , δηλαδή κ' = κ , οπότε και υ'=υ . ■

Αποδεικνύεται ότι το θεώρημα ισχύει γενικότερα για οποιουσδήποτε ακέραιους α και β , με και διατυπώνεται ως εξής:

Αν α και β ακέραιοι με , τότε υπάρχουν μοναδικοί ακέραιοι κ και υ, τέτοιοι, ώστε

Η διαδικασία εύρεσης των κ, υ λέγεται ευκλείδεια ή αλγοριθμική διαίρεση του α με τον β. Το κ λέγεται πηλίκο και το υ υπόλοιπο της διαίρεσης αυτής. Όταν το υπόλοιπο μιας ευκλείδειας διαίρεσης είναι ίσο με το 0, η διαίρεση λέγεται τέλεια.

Ας δούμε με παραδείγματα πώς εργαζόμαστε στις διάφορες περιπτώσεις, για να βρούμε το πηλίκο και το υπόλοιπο μιας ευκλείδειας διαίρεσης.

• Έστω λοιπόν α= -92 με τον β= 5 . Από τη διαίρεση του 92 με τον 5 έχουμε 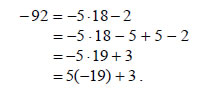και επομένως,

Άρα, , που σημαίνει ότι το πηλίκο της διαίρεσης του -92 με τον 5 είναι -19 και το υπόλοιπο είναι 3.

• Έστω τώρα α= -92 και β= -5. Από την ισότητα 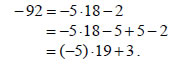έχουμε διαδοχικά

Άρα, , που σημαίνει ότι το πηλίκο της διαίρεσης του -92 με τον -5 είναι 19 και το υπόλοιπο είναι 3.

• Έστω, τέλος, α= 92 και β= -5 . Πάλι από την ισότητα έχουμε:

που σημαίνει ότι το πηλίκο της διαίρεσης του 92 με τον -5 είναι -18 και το υπόλοιπο είναι 2.

ΣΧΟΛΙΟ

Όταν ο διαιρέτης της ευκλείδειας διαίρεσης είναι ο β= 2 , τότε τα δυνατά υπόλοιπα είναι υ=0 ή υ=1 .

Αν υ=0, ο ακέραιος α έχει τη μορφή και λέγεται άρτιος, ενώ

Αν υ=1 , ο ακέραιος έχει τη μορφή και λέγεται περιττός.

Γενικά, τα δυνατά υπόλοιπα του α με τον είναι οι αριθμοί

ΕΦΑΡΜΟΓΕΣ

1. Αν ο α είναι ακέραιος, τότε και ο είναι ακέραιος.

ΑΠΟΔΕΙΞΗ

Επειδή τα δυνατά υπόλοιπα του α με τον 3 είναι 0, 1, 2, ο ακέραιος α έχει μία από τις μορφές .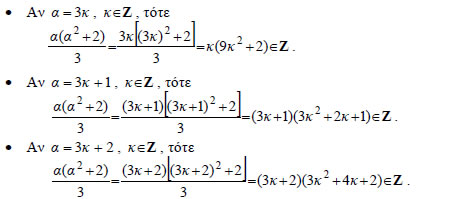

2. Να αποδειχτεί ότι:

(i) Το γινόμενο δύο διαδοχικών ακεραίων είναι άρτιος αριθμός.

(ii) Το τετράγωνο κάθε περιττού ακεραίου είναι της μορφής .

ΑΠΟΔΕΙΞΗ

(i) Έστω δύο διαδοχικοί ακέραιοι α, α+1 .

• Αν ο α είναι άρτιος, δηλαδή , τότε

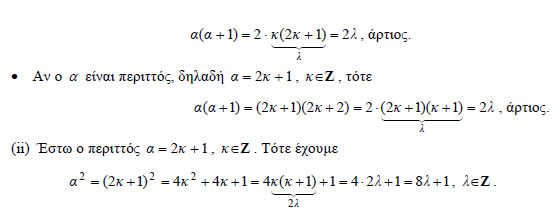
Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε το πηλίκο και το υπόλοιπο της ευκλείδειας διαίρεσης του α με τον β σε καθεμιά από τις παρακάτω περιπτώσεις:
2.	Να αποδείξετε ότι:
3.	Αν α είναι ένας περιττός ακέραιος, να αποδείξετε ότι
4.	Μπορεί ο αριθμός 25 να γραφεί ως άθροισμα 10 προσθετέων, καθένας από τους οποίους να είναι ίσος με 1 ή 3 ή 5;