4ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ

4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ

Εισαγωγή

Η Θεωρία Αριθμών, δηλαδή η μελέτη των ιδιοτήτων των θετικών ακεραίων, έθεσε από πολύ νωρίς τους μαθηματικούς μπροστά στο εξής πρόβλημα:

"Κάποια πρόταση αληθεύει για ορισμένες περιπτώσεις ακεραίων. Είναι όμως αδύνατο να εξεταστούν όλες οι ειδικές περιπτώσεις. Πώς μπορούμε να αποδείξουμε ότι αληθεύει γενικά;"

Μια από τις πλέον ισχυρές μεθόδους για τη λύση αυτού του προβλήματος είναι η μέθοδος της μαθηματικής επαγωγής. Ο (ελληνικής καταγωγής) Ιταλός μαθη-ματικός Francesco Mauroliko (Μαυρόλυκος) απέδειξε το 1557 ότι:

"Το άθροισμα ενός πλήθους περιττών σε διαδοχική σειρά, με αφετη-ρία τη μονάδα, δίνει το τετράγωνο του πλήθους των περιττών."

[δηλαδή, με σύγχρονο συμβολισμό, 1+3+5+...+(2ν -1)=ν²] .

Για την απόδειξη ο Μαυρόλυκος χρησιμοποίησε την πρόταση

"Κάθε τετράγωνο, όταν αυξάνεται με τον επόμενό του στην τάξη περιττό, δίνει το επόμενο στην τάξη τετράγωνο".

[δηλαδή την ταυτότητα ν² + (2ν +1)= (ν+1)²] .

Ουσιαστικά έδειξε λοιπόν ότι υπάρχει ένας γενικός τρόπος μετάβασης από μια περίπτωση στην αμέσως επόμενη. Η μέθοδος αυτή διατυπώθηκε με σαφήνεια από τον Blaise Pascal, το 1654, στην πραγματεία του για το αριθμητικό τρίγωνο. Διατυπώνοντας μια ιδιότητα που ισχύει σε όλες τις γραμμές του τριγώνου, ο Pascal έγραψε τα εξής:

"Αν η πρόταση αυτή έχει έναν άπειρο αριθμό περιπτώσεων, θα δώσω μια πολύ σύντομη απόδειξη υποθέτοντας δύο λήμματα.

Το πρώτο, που είναι προφανές, είναι ότι αυτή η ιδιότητα ισχύει στη 2η γραμμή.

Το δεύτερο είναι ότι αν αυτή η ιδιότητα ισχύει σε μια τυχαία γραμμή, τότε θα ισχύει απαραίτητα και στην επόμενη γραμμή.

Από αυτό γίνεται φανερό ότι η πρόταση αληθεύει σε κάθε περίπτωση, γιατί η ιδιότητα ισχύει στη 2η γραμμή, λόγω του πρώτου λήμματος. Έτ-

σι λόγω του δευτέρου λήμματος θα ισχύει και στην 3η γραμμή, άρα και στην 4η κ.ο.κ., μέχρι το άπειρο."

Οι όροι "μαθηματική επαγωγή" ή "τέλεια επαγωγή", καθιερώθηκαν στη διάρκεια του 19ου αιώνα με τις εργασίες των A. de Morgan (1838) και R. Dedekind (1887), για να γίνει διάκριση από την "ατελή επαγωγή" που χρησιμοποιείται στις Φυσικές Επιστήμες.

Αρχή Μαθηματικής Επαγωγής

Ας υποθέσουμε ότι θέλουμε να βρούμε το άθροισμα

για οποιοδήποτε θετικό ακέραιο ν.

Υπολογίζουμε το άθροισμα αυτό για μερικές τιμές του ν και έχουμε: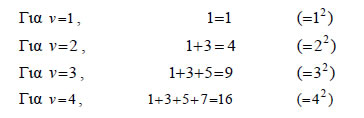

Τα μέχρι τώρα αποτελέσματα μας οδηγούν στην εικασία ότι:

Επειδή το πλήθος των θετικών ακεραίων είναι άπειρο, συνεχίζοντας με τον παραπάνω τρόπο, είναι αδύνατο να αποδείξουμε ότι η (1) ισχύει για όλους τους θετικούς ακεραίους.

Αν όμως μπορούσαμε να δείξουμε ότι όταν αληθεύει ο ισχυρισμός (1) για αυ-θαίρετο θετικό ακέραιο ν θα αληθεύει και για τον επόμενό του ν+1 , τότε ο ισχυρισμός θα ίσχυε για όλους τους θετικούς ακεραίους. Γιατί τότε, αφού ο ισχυρισμός είναι αληθής για ν=1 , θα είναι αληθής και για ν=1+1=2 , συνεπώς και για ν=2+1=3 και διαδοχικά για κάθε θετικό ακέραιο.

Αν, λοιπόν, υποθέσουμε ότι

τότε θα έχουμε: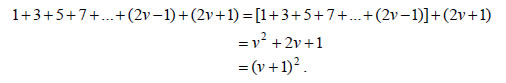

Αποδείξαμε δηλαδή ότι αν ο ισχυρισμός είναι αληθής για έναν αυθαίρετο θετικό ακέραιο ν, τότε είναι αληθής και για τον επόμενό του ακέραιο ν+1 . Άρα, αληθεύει για κάθε θετικό ακέραιο ν.

Μια αναπαράσταση του γεγονότος αυτού είναι η εξής:

Υποθέτουμε ότι έχουμε τοποθετήσει σε μια σειρά ένα πλήθος βιβλίων.

Αν ρίξουμε προς τα πίσω το πρώτο βιβλίο και αν τα βιβλία είναι έτσι τοποθετημένα ώστε κάθε φορά που πέφτει κάποιο βιβλίο να ρίχνει και το επόμενό του, τότε θα ανατραπούν όλα τα βιβλία.

Η αποδεικτική αυτή μέθοδος λέγεται μαθηματική ή τέλεια επαγωγή και στηρίζεται στη λεγόμενη "αρχή της μαθηματικής επαγωγής", η οποία διατυπώνεται ως εξής:

ΑΡΧΗ ΤΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΕΠΑΓΩΓΗΣ

Έστω P(ν) ένας ισχυρισμός που αναφέρεται στους θετικούς ακεραίους.

Αν

(i) ο ισχυρισμός είναι αληθής για τον ακέραιο 1, δηλαδή ο P(1) είναι αληθής, και

(ii) η αλήθεια του P(ν) συνεπάγεται την αλήθεια του P(ν +1) για κάθε ν τότε ο ισχυρισμός P(ν) αληθεύει για όλους τους θετικούς ακεραίους ν .

Όπως φαίνεται από τα προηγούμενα, η μέθοδος της μαθηματικής επαγωγής α-ποτελείται από δύο βήματα. Και τα δύο βήματα είναι απολύτως αναγκαία, για να εξασφαλίσουμε την αλήθεια ενός ισχυρισμού, διότι διαφορετικά μπορεί να οδηγηθούμε σε λάθος συμπεράσματα. Υπάρχουν, δηλαδή, περιπτώσεις στις οποίες ικανοποιείται το 1ο βήμα χωρίς όμως να ικανοποιείται και το 2ο. Για παράδειγμα, το πολυώνυμο v² - v +41 για v =2 έχει την τιμή 41, που είναι πρώτος αριθμός, (δηλαδή δεν έχει άλλο διαιρέτη εκτός της μονάδας και του εαυτού του). Αλλά και για v=2,3,4,5,6,7,8,9,10 έχουμε τις τιμές 43,47,53,61,71,83,97,113,131 αντιστοίχως, που είναι όλοι επίσης πρώτοι αριθμοί. Θα μπορούσε λοιπόν κάποιος να υποθέσει ότι για οποιοδήποτε φυσικό ν η τιμή του πολυώνυμου v² - v +41 είναι πρώτος αριθμός. Αυτό όμως, ενώ ισχύει μέχρι και v =40 , δεν ισχύει για v =41, για το οποίο έχουμε 41² -41+41=41² , που δεν είναι πρώτος.

Υπάρχουν επίσης περιπτώσεις στις οποίες ικανοποιείται το 2ο βήμα της μαθη-ματικής επαγωγής χωρίς όμως να ικανοποιείται και το 1ο. Ας θεωρήσουμε, για παράδειγμα, τον ισχυρισμό:

"Κάθε φυσικός της μορφής 2ν είναι περιττός".

Αν και ο ισχυρισμός είναι προφανώς ψευδής, ωστόσο ισχύει το 2ο βήμα της μαθηματικής επαγωγής. Πράγματι, αν ο αριθμός 2v με ν φυσικό είναι περιττός, τότε 2(v+1)=2v+2 είναι επίσης περιττός, ως άθροισμα του περιττού 2v με τον άρτιο 2.

Πολλές φορές πρέπει να αποδείξουμε ότι ένας ισχυρισμός P(v) αληθεύει όχι για κάθε θετικό ακέραιο ν αλλά για κάθε ν μεγαλύτερο ή ίσο από κάποιο ορισμένο φυσικό αριθμό.

Για παράδειγμα, αν θέλουμε να δείξουμε ότι , τότε το πρώτο βήμα είναι να αποδείξουμε την αλήθεια της ανισότητας για v=3 , ενώ αν θέλουμε να αποδείξουμε ότι , τότε το πρώτο βήμα είναι να αποδείξουμε την αλήθεια της ανισότητας για v=0.

ΕΦΑΡΜΟΓΕΣ

1.Να αποδειχτεί ότι για κάθε θετικό ακέραιο v.

ΑΠΟΔΕΙΞΗ

Έστω P(v) η ισότητα που θέλουμε να αποδείξουμε.

• Για v=1 η ισότητα γίνεται ή ισοδύναμα 1=1, δηλαδή η P(1) είναι αληθής.

• Θα αποδείξουμε ότι αν P(v) αληθής, τότε και P(v +1) αληθής, δηλαδή ότι: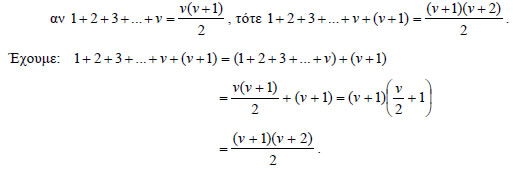

Άρα, η ισότητα αληθεύει για όλους τους θετικούς ακεραίους ν.

2.Να αποδειχτεί ότι για όλους τους θετικούς ακεραίους v με και για όλους τους πραγματικούς α με .

ΑΠΟΔΕΙΞΗ

Έστω P(v) η ανισότητα που θέλουμε να αποδείξουμε.

• Για v=2 η ανισότητα γίνεται: που είναι αληθής, αφού για . Ώστε P(2) αληθής.

• Θα αποδείξουμε ότι αν P(v) αληθής, τότε και P(v +1) αληθής, δηλαδή:

Έχουμε διαδοχικά: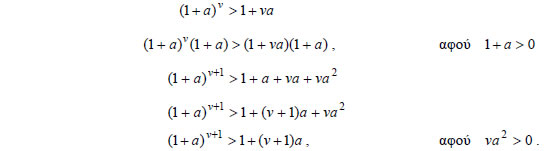

Επομένως, η ανισότητα του Bernoulli ισχύει για όλους τους θετικούς ακεραίους v με .

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ
1.	Να αποδείξετε ότι για κάθε θετικό ακέραιο ν ισχύει