4.3 ΔΙΑΙΡΕΤΟΤΗΤΑ

Εισαγωγή

Στα "Στοιχεία" του Ευκλείδη, βιβλία VII, VIII και IX (περίπου 300 π.Χ.), οι θετικοί ακέραιοι παριστάνονται ως ευθύγραμμα τμήματα και η έννοια της διαι-ρετότητας συνδέεται άμεσα με τη μέτρηση των ευθύγραμμων τμημάτων. Ο Ευκλείδης στην αρχή του βιβλίου VII δίνει 22 ορισμούς, μεταξύ των οποίων και οι εξής:

Διαιρέτης: Μέρος εστίν αριθμός αριθμού ο ελάσσων του μείζονος, όταν καταμετρή τον μείζονα.
Πολλαπλάσιο: Πολλαπλάσιος δε ο μείζων του ελάσσονος, όταν καταμετρήται υπό του ελάσσονος.
Άρτιος αριθμός: Άρτιος αριθμός έστιν ο δίχα διαιρούμενος.
Περιττός αριθμός: Περισσός δε ο μη διαιρούμενος δίχα ή ο μονάδι διαφέρων αρτίου αριθμού.
Πρώτος αριθμός: Πρώτος αριθμός έστιν ο μονάδι μόνη μετρούμενος.

Πρώτοι μεταξύ τους: Πρώτοι προς αλλήλους αριθμοί εισίν οι μονάδι μετρούμενοι κοινώ μέτρω.

Τελευταίος δίνεται ο ορισμός του τέλειου αριθμού, δηλαδή αυτού που είναι ίσος με το άθροισμα των γνήσιων διαιρετών του, για παράδειγμα, 28=1+ 2+ 4 + 7 +14 :

Τέλειος αριθμός έστιν ο τοις εαυτού μέρεσιν ίσος ών.

Το ενδιαφέρον των αρχαίων μαθηματικών για τους τέλειους αριθμούς φαίνεται ότι προκλήθηκε από την εξαιρετική σπανιότητά τους. Είναι χαρακτηριστική η παρατήρηση του M. Mersenne (1588-1642) ότι "οι τέλειοι αριθμοί είναι τόσο σπάνιοι όσο και οι τέλειοι άνθρώποι".

Η Θεωρία Αριθμών αρχίζει στο βιβλίο VII με δύο προτάσεις για την εύρεση του μέγιστου κοινού διαιρέτη δύο αριθμών (Ευκλείδειος αλγόριθμος) και ολοκλη-ρώνεται στην τελευταία πρόταση του βιβλίου IX με μια μέθοδο προσδιορισμού τέλειων αριθμών. Με σύγχρονο συμβολισμό, στην πρόταση αυτή ο Ευκλείδης αποδεικνύει ότι:

Αν ο αριθμός 1+2+2²+...+2^v-1=2^v-1 είναι πρώτος, τότε ο αριθμός 2^v-1(2^v -1) είναι τέλειος.

Έτσι, η γνώση ενός πρώτου αριθμού της μορφής 2^v-1 οδηγεί αμέσως στην ανακάλυψη ενός τέλειου αριθμού. Οι πρώτοι 5 αριθμοί αυτού του είδους είναι οι 2²-1=3 , 2³-1=7 ,2⁵-1=31 ,2⁷-1=127, 2¹³-1=8191 και μας δίνουν τους πρώτους 5 τέλειους αριθμούς 6,28,496,8128 και 33550336. Μέχρι σήμερα έχουν βρεθεί 36 τέλειοι αριθμοί.

Έννοια Διαιρετότητας

Στην ευκλείδεια διαίρεση ιδιαίτερο ενδιαφέρον παρουσιάζει η περίπτωση κατά την οποία το υπόλοιπο είναι ίσο με μηδέν, δηλαδή η περίπτωση της τέλειας διαίρεσης. Την περίπτωση αυτή θα εξετάσουμε στη συνέχεια.

ΟΡΙΣΜΟΣ

Έστω α, β δύο ακέραιοι με . Θα λέμε ότι ο β διαιρεί τον α και θα γράφουμε , όταν η διαίρεση του α με τον β είναι τέλεια, δηλαδή όταν υπάρχει ακέραιος κ, τέτοιος, ώστε α = κβ .

Στην περίπτωση αυτή λέμε επίσης ότι ο β είναι διαιρέτης ή παράγοντας του α ή ότι ο α διαιρείται με τον β ή ακόμα ότι ο α είναι πολλαπλάσιο του β, και γράφουμε α = πολβ .

Για να δηλώσουμε ότι ο ακέραιος β δε διαιρεί τον ακέραιο α , γράφουμε ή ισοδύναμα . Για παράδειγμα, , ενώ , αφού η διαίρεση του 18 με τον 5 δεν είναι τέλεια.

Αν , τότε α= κβ ή ισοδύναμα α= (- κ)( -β) , που σημαίνει ότι αν ο β είναι διαιρέτης του α, τότε και ο -β είναι διαιρέτης του α . Επομένως, οι διαιρέτες ενός ακέραιου εμφανίζονται κατά ζεύγη αντίθετων ακέραιων.

Ως άμεσες συνέπειες του παραπάνω ορισμού έχουμε τις εξής: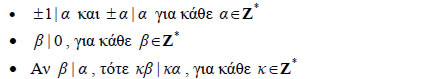

Τονίζουμε ότι στο συμβολισμό , οι αριθμοί α και β είναι πάντα ακέραιοι και .

Θα γνωρίσουμε τώρα μερικές χρήσιμες ιδιότητες της διαιρετότητας.

ΘΕΩΡΗΜΑ 2

Έστω α,β,γ ακέραιοι. Ισχύουν οι ακόλουθες ιδιότητες

ΑΠΟΔΕΙΞΗ

Από τις ιδιότητες (iii) και (iv) του παραπάνω θεωρήματος προκύπτει ότι:

"Αν , τότε για όλους τους ακεραίους κ και λ."

Ο ακέραιος κβ + λγ , όπου λέγεται γραμμικός συνδυασμός των β και γ.

ΕΦΑΡΜΟΓΕΣ

1. Αν α,δ ακέραιοι με , να βρεθούν οι πιθανές θετικές τιμές του δ.

ΛΥΣΗ

Επειδή , ο δ διαιρεί και τον . Αφού λοιπόν , θα είναι δ=1 ή δ=5 .

2. Να αποδειχτεί ότι 9^v+1 -8v -9=πολ64, για κάθε .

ΑΠΟΔΕΙΞΗ

Θα αποδείξουμε την πρόταση με τη μέθοδο της μαθηματικής επαγωγής.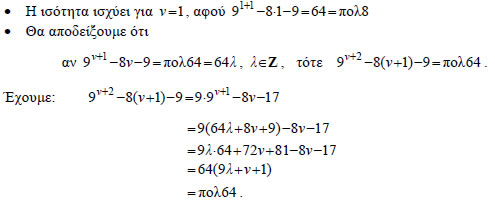

Άρα η ισότητα αληθεύει για όλους τους θετικούς ακεραίους.

3. Να αποδειχτεί ότι ο 3 διαιρεί τους ακεραίους α και β , αν και μόνο αν ο 3 διαιρεί το άθροισμα α²+β².

ΑΠΟΔΕΙΞΗ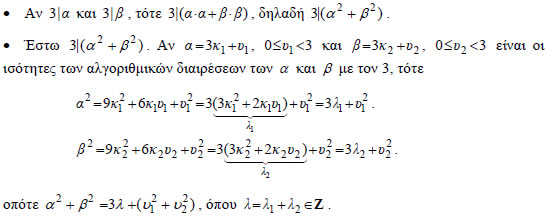

Επειδή . Όμως οπότε, για τις τιμές της παράστασης , έχουμε τον παρακάτω πίνακα:

Από τον πίνακα αυτόν προκύπτει ότι , μόνο όταν υ₁=0 και υ₂=0 , δηλαδή μόνο όταν α=3κ₁ και β=3κ₂ , που σημαίνει ότι .

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε το πλήθος των θετικών ακεραίων που δεν υπερβαίνουν τον 1000 και διαιρούνται με:
2.	Αν , να αποδείξετε ότι .
3.	Αν , να αποδείξετε ότι .
4.	Αν η διαφορά δύο ακεραίων είναι άρτιος αριθμός, να αποδείξετε ότι η διαφορά των τετραγώνων τους είναι πολλαπλάσιο του 4.
5.	Αν , να αποδείξετε ότι .