3.5 Η ΕΞΙΣΩΣΗ

3.5 Η ΕΞΙΣΩΣΗ Ax²+ By² + Γx + Δy + E

Μεταφορά Αξόνων

Η εξίσωση ενός κύκλου με ακτίνα ρ έχει την απλή μορφή x² + y² = ρ², αν η αρχή του συστήματος συντεταγμένων O(0,0) είναι το κέντρο του κύκλου. Αν όμως το κέντρο του κύκλου δεν είναι η αρχή των αξόνων αλλά το σημείο O'(x₀,y₀) , τότε η εξίσωσή του έχει την πιο σύνθετη μορφή (x - x₀)² + (y -y₀)² =ρ ² . Αυτό δείχνει ότι η μορφή της εξίσωσης μιας καμπύλης εξαρτάται από τη σχετική θέση της καμπύλης και των αξόνων.

Ας υποθέσουμε ότι σε ένα επίπεδο έχουμε μια καμπύλη και την εξίσωσή της ως προς ένα σύστημα συντεταγμένων Oxy . Θα αναζητήσουμε την εξίσωση της ίδιας καμπύλης ως προς ένα "νέο" σύστημα συντεταγμένων, του οποίου η αρχή θα είναι το σημείο O'(x₀,y₀) και οι άξονες X'OX και Y'OY θα είναι παράλληλοι και ομόρροποι προς τους άξονες του "παλιού" συστήματος. Λέμε στην περίπτωση αυτή ότι το σύστημα O'XY έχει προκύψει με παράλληλη μεταφορά των αξόνων του συστήματος Oxy.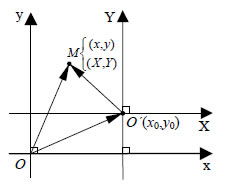

Έστω λοιπόν x και y οι συντεταγμένες ενός σημείου Μ ως προς το παλιό σύστημα, και X και Y οι συντεταγμένες του ίδιου σημείου ως προς το νέο σύστημα. Έχουμε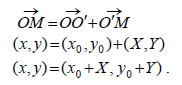

Επομένως, x=x₀ + X και y=y₀ + Y ή, ισοδύναμα,

Έτσι για παράδειγμα, αν οι συντεταγμένες ενός σημείου Μ ως προς ένα καρτεσιανό σύστημα είναι (4, -3) και η αρχή O(0,0) μετακινηθεί με τη μεταφορά των αξόνων στο σημείο O'( -1,2) , τότε οι νέες συντεταγμένες του Μ είναι X =4 - ( -1)=5 και Y = -3 -2= -5 .

Έστω επίσης η εξίσωση (x - 2)² + (y +1)² = 9 , που παριστάνει κύκλο με κέντρο K(2, -1) και ακτίνα ρ=3. Αν με μια παράλληλη μεταφορά των αξόνων η αρχή O(0,0) μετακινηθεί στο κέντρο του κύκλου, τότε οι καινούριες

συντεταγμένες (X,Y) ενός σημείου Μ του κύκλου είναι X= x - 2 και Y = y - (-1) = y + 1. Επομένως η εξίσωση του κύκλου ως προς το νέο σύστημα αξόνων έχει την απλούστερη μορφή X²+ Y²=9.

ΕΦΑΡΜΟΓΗ

Να εξεταστεί τι παριστάνει στο επίπεδο καθεμιά από τις εξισώσεις: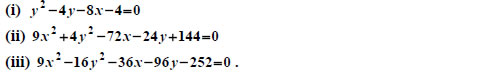

ΛΥΣΗ

(i) Έχουμε διαδοχικά: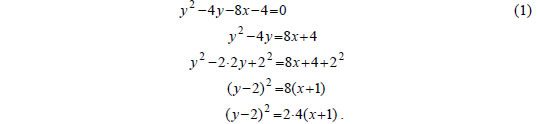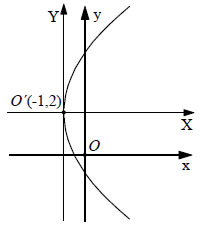

Αν θέσουμε x+1=X και y -2=Y , δηλαδή αν κάνουμε παράλληλη μεταφορά των αξόνων και τοποθετήσουμε τη νέα αρχή στο σημείο O'(-1, 2) , τότε η εξίσωση παίρνει τη μορφή

Επομένως, η εξίσωση (1) παριστάνει παραβολή με κορυφή το σημείο O'( -1,2) και άξονα την ευθεία Y=0 , δηλαδή την ευθεία y=2.

(ii) Έχουμε διαδοχικά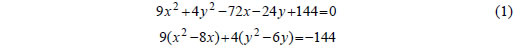

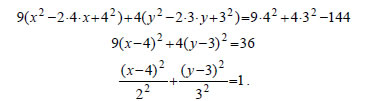Αν θέσουμε x - 4=X και y - 3=Y , δηλαδή αν κάνουμε παράλληλη μεταφορά των αξόνων και τοποθετήσουμε τη νέα αρχή στο σημείο O'(4,3) , τότε η εξίσωση παίρνει τη μορφή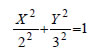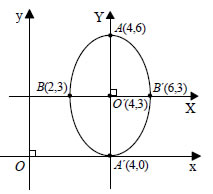

Επομένως, η εξίσωση (1) παριστάνει έλλειψη με κέντρο το σημείο O'(4,3) και με α=3, β=2 και . Τα άκρα του μεγάλου άξονα ως προς το νέο σύστημα είναι τα σημεία (Χ,Υ)=(0,3) και (Χ,Υ)=(0, -3) , οπότε, λόγω των σχέσεων x -4=X και y -3=Y , ως προς το αρχικό σύστημα, είναι τα σημεία A(4,6) και A'(4,0). Ανάλογα βρίσκουμε ότι τα άκρα του μικρού άξονα είναι τα σημεία B(2,3) και B'(6,3) . Επίσης, οι εστίες είναι τα σημεία .

(iii) Έχουμε διαδοχικά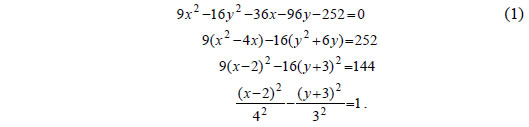

Αν θέσουμε x -2=X και y +3=Y, δηλαδή αν κάνουμε παράλληλη μεταφορά των αξόνων και τοποθετήσουμε τη νέα αρχή στο σημείο O'(2, -3) , τότε η εξίσωση παίρνει τη μορφή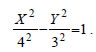

Επομένως, η εξίσωση (1) παριστάνει υπερβολή με κέντρο το σημείο O'(2, -3) . Με ανάλογο τρόπο, όπως στην περίπτωση (ii), βρίσκουμε ότι η υπερβολή αυτή έχει

Άρα, η υπερβολή έχει κορυφές τα σημεία A(6, -3) και A'( -2, -3) και εστίες E(7, -3) και E'(-3, -3) .

Γενικά, με κατάλληλη μεταφορά αξόνων, μπορούμε να διαπιστώσουμε αν μια εξίσωση της μορφής Ax² + By² + Γx + Δy + E = 0 παριστάνει κωνική τομή και να βρούμε το είδος και τα στοιχεία της.

Σχετική Θέση Ευθείας και Κωνικής

Ας θεωρήσουμε μία ευθεία y=λx+β και μία κωνική τομή Ax² + By² + Γx + Δy + E = 0. Η ευθεία ε και η κωνική C έχουν το πολύ δύο κοινά σημεία, αφού το σύστημα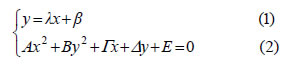

έχει το πολύ δύο διακεκριμένες λύσεις.

Για την επίλυση του συστήματος θέτουμε στη (2), όπου y=λx+β , οπότε προκύπτει μια δευτεροβάθμια εξίσωση.

— Αν η εξίσωση αυτή έχει δύο ρίζες άνισες ή μια απλή ρίζα (όταν είναι 1ου βαθμού), τότε η ευθεία και η κωνική τέμνονται.

— Αν η εξίσωση έχει δύο ρίζες ίσες, δηλαδή αν είναι 2ου βαθμού με διακρίνουσα Δ = 0, τότε αποδεικνύεται ότι η ευθεία εφάπτεται της κωνικής.

— Τέλος, αν η εξίσωση δεν έχει ρίζες, τότε η ευθεία και η κωνική δεν έχουν κοινά σημεία.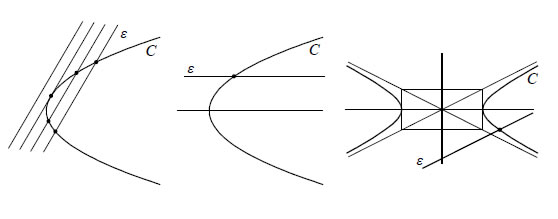

Για παράδειγμα, έστω η ευθεία y=2x και η παραβολή y=x²+1 . Αν στην εξίσωση της παραβολής θέσουμε όπου y=2x , βρίσκουμε τη δευτεροβάθμια εξίσωση x² -2x +1=0 , η οποία έχει τη διπλή ρίζα x=1 . Άρα, η ευθεία εφάπτεται της κωνικής και το σημείο επαφής είναι το M(1,2).

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να αποδείξετε ότι καθεμιά από τις παρακάτω εξισώσεις παριστάνει παραβολή, για την οποία να βρείτε τις συντεταγμένες της κορυφής και της εστίας:
2.	Να αποδείξετε ότι καθεμιά από τις παρακάτω εξισώσεις παριστάνει έλλειψη, για την οποία να βρείτε τις συντεταγμένες του κέντρου, των κορυφών και των εστιών.
3.	Να αποδείξετε ότι καθεμιά από τις παρακάτω εξισώσεις παριστάνει υπερβολή, για την οποία να βρείτε τις συντεταγμένες του κέντρου, των κορυφών και των εστιών:
4.	Να βρεθεί η τιμή του , για την οποία η παραβολή y=x² -κx +2 εφάπτεται της ευθείας y=x -2 .
5.	Να βρείτε τις κοινές εφαπτόμενες του κύκλου και της παραβολής y²=4x .

ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ

Δίνεται η εξίσωση

(i) Να αποδείξετε ότι για κάθε τιμή του λ η (1) παριστάνει κύκλο του οποίου ζητείται να βρεθεί το κέντρο και η ακτίνα.

(ii) Να αποδείξετε ότι όλοι οι κύκλοι C_λ που ορίζονται από την (1) για τις διάφορες τιμές του λ διέρχονται από δύο σταθερά σημεία. Ποιά είναι η εξίσωση της κοινής χορδής όλων αυτών των κύκλων;

2	Δίνονται οι κύκλοι και η ευθεία y=λx+β, όπου . (i) Ποιες είναι οι αποστάσεις των κέντρων των κύκλων C₁ και C₂ από την ευθεία; (ii) Για ποιες τιμές των λ και β η ευθεία εφάπτεται και στους δύο κύκλους; (iii) Να αποδείξετε ότι οι κοινές εφαπτόμενες των κύκλων C₁ και C₂ τέμνονται πάνω στον άξονα x'x και σχηματίζουν μεταξύ τους γωνία .
3.	Μια ευθεία y=λx+β, με , τέμνει την παραβολή y²=4x σε δύο σημεία Α και Β. (i) Να αποδείξετε ότι οι συντεταγμένες του μέσου Μ του ΑΒ είναι . (ii) Να βρείτε την εξίσωση της γραμμής πάνω στην οποία βρίσκεται το Μ, όταν (α) λ=1 και το β μεταβάλλεται (β) β=0 και το λ μεταβάλλεται.
4.	Δίνεται η έλλειψη και το σημείο Σ(0,2β). Μια ευθεία με συντελεστή διεύθυνσης λ διέρχεται από το σημείο Σ και τέμνει τις εφαπτόμενες, στα άκρα του μεγάλου άξονα της έλλειψης, στα σημεία Μ και M' . (i) Να βρείτε την εξίσωση του κύκλου με διάμετρο MM' συναρτήσει του λ. (ii) Για ποιες τιμές του ο κύκλος αυτός διέρχεται από τις εστίες της έλλειψης;
5.	Δίνεται η έλλειψη . Να βρείτε την εξίσωση της υπερβολής η οποία έχει τις ίδιες εστίες με την έλλειψη και εφάπτεται στην ευθεία y=x +1 .
6.	Έστω τα διανύσματα του καρτεσιανού επιπέδου. Αν τα διανύσματα αρχίσουν, συγχρόνως, να περιστρέφονται με την ίδια γωνιακή ταχύτητα αλλά με αντίθετη φορά, να αποδείξετε ότι το πέρας Μ της συνισταμένης τους διαγράφει έλλειψη.
7.	Δίνονται οι ημιευθείες και μια ευθεία ε η οποία τις τέμνει στα σημεία M₁ και M₂ αντιστοίχως. (i) Να βρείτε τις συντεταγμένες των M₁ και M₂ συναρτήσει των συντεταγμένων του μέσου Μ του ευθύγραμμου τμήματος M₁M₂ . (ii) Να αποδείξετε ότι όταν η ευθεία ε κινείται, έτσι ώστε το τρίγωνο OM₁M₂ να έχει σταθερό εμβαδόν και ίσο με 2, τότε το Μ κινείται στον ένα κλάδο μίας σταθερής υπερβολής.

8	Δίνονται οι ελλείψεις . Η ημιευθεία τέμνει την C₁ στο σημείο Γ₁(x₁,y₁) και την C₂ στο σημείο Γ₂(x₂,y₂) . Αν λ₁ είναι ο συντελεστής διεύθυνσης της εφαπτομένης της C₁ στο σημείο Γ₁ και λ₂ είναι ο συντελεστής διεύθυνσης της εφαπτομένης της C₂ στο σημείο Γ₂, να αποδείξετε ότι το γινόμενο λ₁λ₂ είναι ίσο με .
9.	Δίνεται η έλλειψη . (i) Η εφαπτομένη της έλλειψης στο σημείο που η διχοτόμος του πρώτου τεταρτημόριου τέμνει την έλλειψη έχει κλίση -1/2. Να βρείτε την εκκεντρότητα της έλλειψης. (ii) Έστω Μ το σημείο του πρώτου τεταρτημόριου στο οποίο η ευθεία y=λx, τέμνει την παραπάνω έλλειψη. Αν μ είναι η κλίση της εφαπτόμενης της έλλειψης στο σημείο Μ, τότε να εκφράσετε το γινόμενο λμ ως συνάρτηση των ημιαξόνων α, β.
10.	(i) Δίνονται ένας κύκλος C₁ με κέντρο Κ και ακτίνα R και μια ευθεία ε που δεν έχει κανένα κοινό σημείο με τον κύκλο C₁ . Να αποδείξετε ότι τα κέντρα των κύκλων C, που εφάπτονται της ε και του κύκλου C₁ εξωτερικά, ανήκουν σε σταθερή παραβολή. (ii) Δίνονται δύο κύκλοι C₁ και C₂ , με κέντρα K₁ και K₂ και ακτίνες R₁ και R₂ αντιστοίχως, από τους οποίους ο C₂ είναι εσωτερικός του C₁ . Να αποδείξετε ότι τα κέντρα των κύκλων C, που εφάπτονται εσωτερικά του C₁ και εξωτερικά του C₂ , ανήκουν σε σταθερή έλλειψη. (iii) Δίνονται δύο κύκλοι C₁ και C₂ , με κέντρα K₁ και K₂ και ακτίνες R₁ και R₂, αντιστοίχως, που βρίσκονται ο ένας εκτός του άλλου. Να αποδείξετε ότι τα κέντρα του κύκλου C που εφάπτονται εξωτερικά και των δύο κύκλων C₁ και C₂ ανήκουν σε κλάδο σταθερής υπερβολής.
11.	Δίνεται η έλλειψη και το σημείο της . (i) Να βρείτε την εξίσωση της εφαπτομένης της έλλειψης στο σημείο Μ. (ii) Να αποδείξετε ότι το γινόμενο των αποστάσεων των εστιών Ε και E' από την εφαπτομένη είναι σταθερό. (iii) Για ποια τιμή του φ το εμβαδόν του τριγώνου που ορίζει η εφαπτομένη με τους άξονες γίνεται ελάχιστο;

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

	Στις παρακάτω ερωτήσεις 1-11 να βάλετε σε κύκλο τη σωστή απάντηση:
1.	Ο κύκλος (x - α)² +y² = α² Α) εφάπτεται στον x'x Β) διέρχεται από το σημείο A(0,α) Γ) εφάπτεται στον y'y .
2.	Η ευθεία y=x+1 και ο κύκλος x²+y²=1 Α) τέμνονται Β) εφάπτονται Γ) δεν έχουν κοινά σημεία.
3.	Έστω οι κύκλοι . Το σημείο M(1,1) είναι Α) εσωτερικό του ενός κύκλου και εξωτερικό του άλλου Β) σημείο και των δύο κύκλων Γ) εσωτερικό και των δύο κύκλων Δ) εξωτερικό και των δύο κύκλων.
4.	Έστω ο κύκλος με παραμετρικές εξισώσεις: Το σημείο είναι Α) εσωτερικό του κύκλου Β) εξωτερικό του κύκλου Γ) σημείο του κύκλου.
5.	Στο διπλανό σχήμα η δ είναι η διευθετούσα και το Ε είναι η εστία της παραβολής y²=2px . Το μήκος της χορδής ΑΒ είναι ίσο με:

6.	Στο διπλανό σχήμα τα σημεία E,E' είναι οι εστίες της έλλειψης . Το μήκος του ΒΕ είναι Α) μεγαλύτερο του α, Β) μικρότερο του α, Γ) ίσο με α.
7.	Στο ίδιο σχήμα αν το τρίγωνο BEE' είναι ισόπλευρο, τότε η εκκεντρότητα της έλλειψης είναι ίση με
8.	Αν οι ελλείψεις είναι όμοιες, τότε
9.	Δίνεται η έλλειψη με παραμετρικές εξισώσεις Το σημείο Μ(7,0) είναι
10.	Οι υπερβολές έχουν Α) ίδιες ασύμπτωτες και ίδια εκκεντρότητα, Β) διαφορετικές ασύμπτωτες και ίδια εκκεντρότητα, Γ) ίδιες ασύμπτωτες και διαφορετική εκκεντρότητα, Δ) διαφορετικές ασύμπτωτες και διαφορετικές εκκεντρότητες.
11.	Στο διπλανό σχήμα το ΚΛΜΝ είναι το ορθογώνιο βάσης της υπερβολής . Το μήκος ΟΚ είναι Α) μεγαλύτερο του γ Β) ίσο με γ Γ) μικρότερο του γ.

12.	Έστω ο κύκλος . Να συνδέσετε με μια γραμμή τα δεδομένα της πρώτης στήλης με τα αντίστοιχά τους στη δεύτερη στήλη
13.	Να συνδέσετε με μια γραμμή τα δεδομένα της πρώτης στήλης με τα αντίστοιχά τους στη δεύτερη στήλη
14.	Να συνδέσετε με μια γραμμή τα δεδομένα της πρώτης στήλης με τα αντίστοιχά τους στη δεύτερη στήλη