3.2 Η ΠΑΡΑΒΟΛΗ

Ορισμός Παραβολής

Έστω μια ευθεία δ και ένα σημείο Ε εκτός της δ. Ονομάζεται παραβολή με εστία το σημείο Ε και διευθετούσα την ευθεία δ ο γεωμετρικός τόπος C των σημείων του επιπέδου τα οποία ισαπέχουν από την Ε και τη δ (Σχ. α). Αν Α είναι η προβολή της εστίας Ε στη διευθετούσα δ, τότε το μέσο Κ του ΕΑ είναι προφανώς σημείο της παραβολής και λέγεται κορυφή της.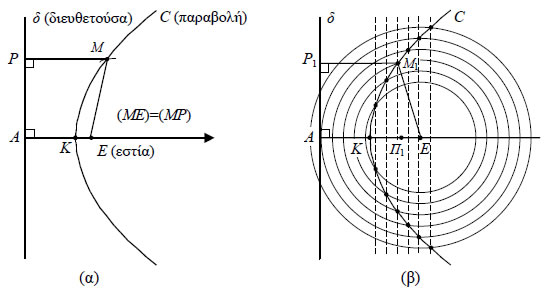

Για να βρούμε ένα σημείο της παραβολής C, εργαζόμαστε ως εξής: Παίρνουμε ένα σημείο Π₁ της ημιευθείας ΚΕ (Σχ. β) και από το σημείο αυτό φέρνουμε την κάθετη στην ΚΕ και έστω M₁ ένα από τα σημεία τομής της κάθετης αυτής και του κύκλου με κέντρο το Ε και ακτίνα Π₁A . Τότε, το σημείο M₁ είναι σημείο της παραβολής C. Πράγματι, αν P₁ είναι η ορθή προβολή του M₁ στη διευθετούσα δ, τότε θα ισχύει , δηλαδή .

Εξίσωση Παραβολής

• Έστω C μια παραβολή με εστία Ε και διευθετούσα δ. Θα βρούμε την εξίσωση της παραβολής C ως προς σύστημα συντεταγμένων Oxy με αρχή Ο την κορυφή της παραβολής και άξονα x'x την κάθετη από το Ε στην δ.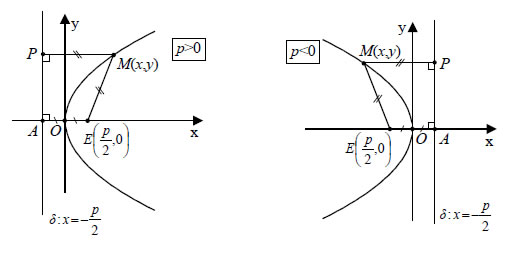

Αν στο σύστημα αυτό η τετμημένη της εστίας Ε είναι p/2 , τότε η εξίσωση της διευθετούσας θα είναι x = − p/2.

Σύμφωνα με τον ορισμό της παραβολής, ένα σημείο M(x,y) θα ανήκει στη C, αν και μόνο αν ισχύει

Είναι όμως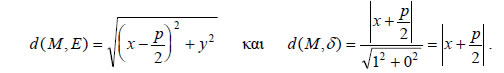

Έτσι, η σχέση (1) γράφεται διαδοχικά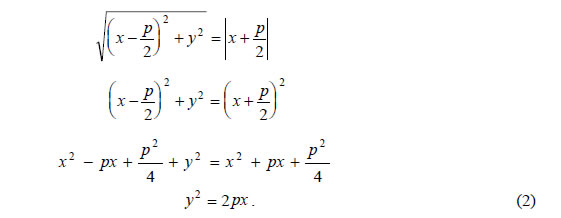

Επομένως, η εξίσωση της παραβολής C με εστία και διευθετούσα είναι

Για παράδειγμα, η παραβολή με εστία το σημείο E(1,0) και διευθετούσα την ευθεία x= −1 έχει p=2 και επομένως έχει εξίσωση y²= 4x .Ο αριθμός p λέγεται παράμετρος της παραβολής και η 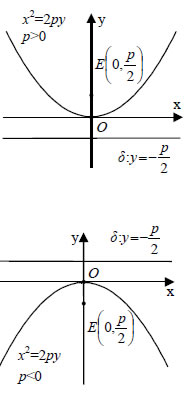παριστάνει την απόσταση της εστίας από τη διευθετούσα.

• Αν τώρα πάρουμε σύστημα συντεταγμένων Oxy με αρχή Ο την κορυφή της παραβολής και άξονα y'y την κάθετη από το Ε στη δ και εργαστούμε όπως πριν, θα βρούμε ότι η παραβολή C έχει εξίσωση

Η εξίσωση αυτή γράφεται ισοδύναμα και παριστάνει τη γραφική παράσταση της γνωστής μας από την Α΄ Λυκείου συνάρτησης

Για παράδειγμα, η εξίσωση παριστάνει την παραβολή που έχει p=2 και άρα έχει εστία το σημείο E(0,1) και διευθετούσα την ευθεία y= −1.

Ιδιότητες Παραβολής

Έστω μια παραβολή

• Από την εξίσωση (1) προκύπτει ότι τα p και x (με ) είναι ομόσημα. Άρα, κάθε φορά η παραβολή βρίσκεται στο ημιεπίπεδο που ορίζει ο άξονας y'y και η εστία Ε. Επομένως, η παραβολή βρίσκεται στο ημιεπίπεδο που ορίζει η διευθετούσα δ και η εστία Ε.

• Αν το σημείο M₁(x₁,y₁) είναι σημείο της παραβολής, δηλαδή, αν y²₁=2px₁ , τότε και το σημείο M₂(x₁, -y₁) θα είναι σημείο της ίδιας παραβολής, αφού ( -y₁ )²=2px₁ . Αυτό σημαίνει ότι ο άξονας x'x είναι άξονας συμμετρίας της παραβολής. Επομένως, η κάθετη από την εστία στη διευθετούσα είναι άξονας συμμετρίας της παραβολής και λέγεται άξονας της παραβολής.

ΕΦΑΡΜΟΓΗ

Έστω η παραβολή y²=2px και μια ευθεία που διέρχεται από την εστία της και τέμνει την παραβολή στα σημεία M₁ και M₂ . Να αποδειχτεί ότι το γινόμενο των αποστάσεων των M₁ και M₂ από τον άξονα x'x είναι σταθερό.

ΑΠΟΔΕΙΞΗ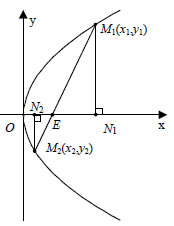

Αν (x₁,y₁) και (x₂,y₂) είναι οι συντεταγμένες των M₁ και M₂ αντιστοίχως, τότε οι αποστάσεις των M₁ και M₂ από τον άξονα x'x θα είναι ίσες με και αντιστοίχως. Επομένως, αρκεί να δείξουμε ότι το είναι σταθερό. Επειδή τα σημεία (x₁,y₁) , (x₂,y₂) ανήκουν στην παραβολή y²=2px , θα ισχύει

Επομένως, οι συντεταγμένες των σημείων M₁ και M₂ θα είναι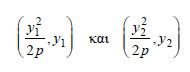

αντιστοίχως.

Όμως, τα σημεία ε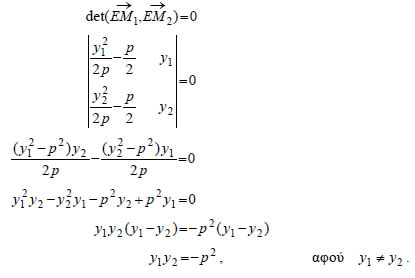ίναι συνευθειακά.

Επομένως: οπότε έχουμε διαδοχικά:

Άρα . (σταθερό)

Εφαπτομένη Παραβολής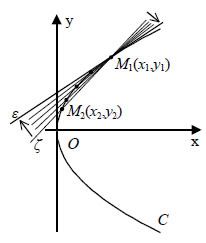

• Έστω μια παραβολή C με εξίσωση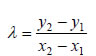

και ένα σταθερό της σημείο M₁(x₁,y₁) . Έστω επιπλέον μια μη κατακόρυφη ευθεία ζ που διέρχεται από το M₁(x₁,y₁) και τέμνει την παραβολή και σε ένα άλλο σημείο M₂(x₂,y₂) . Τότε η ζ θα έχει συντελεστή διεύθυνσης

και επειδή διέρχεται από το σημείο M₁(x₁,y₁), θα έχει εξίσωση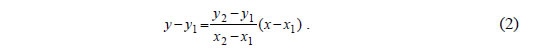

Επειδή τα σημεία M₁(x₁,y₁), M₂(x₂,y₂) ανήκουν στην παραβολή, οι συντεταγμένες τους θα επαληθεύουν την εξίσωση (1). Άρα, θα ισχύει

οπότε θα έχουμε διαδοχικά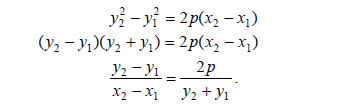

Έτσι, η εξίσωση (2) θα πάρει τη μορφή

δηλαδή τη μορφή

Ας υποθέσουμε τώρα ότι το σημείο M₂(x₂,y₂) , κινούμενο πάνω στην παραβολή C, τείνει να συμπέσει με το σημείο M₁(x₁,y₁) . Τότε το y₂ τείνει να γίνει ίσο με y₁ , οπότε η εξίσωση (3) της τέμνουσας ζ τείνει να πάρει τη μορφή

δηλαδή τη μορφή

Η εξίσωση αυτή παριστάνει την ευθεία ε, που είναι η οριακή θέση της τέμνουσας ζ, καθώς το M₂ τείνει να συμπέσει με το M₁ . Η ευθεία ε λέγεται εφαπτομένη της παραβολής στο σημείο M₁ . Η εξίσωση της εφαπτομένης γράφεται διαδοχικά: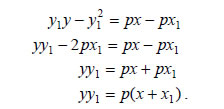

Επομένως, η εφαπτομένη της παραβολής y²=2px στο σημείο της M₁(x₁,y₁) έχει εξίσωση

Για παράδειγμα, η εφαπτομένη της παραβολής y²=4x στο σημείο της M₁(2,1) έχει εξίσωση , η οποία γράφεται y=x+1 .

• Αν μια παραβολή έχει εξίσωση

τότε η εφαπτομένη της στο σημείο M₁(x₁,y₁) έχει εξίσωση

Ανακλαστική Ιδιότητα Παραβολής

Μια σπουδαία ιδιότητα της παραβολής, γνωστή ως ανακλαστική ιδιότητα είναι η εξής:

Η κάθετη στην εφαπτομένη μιας παραβολής στο σημείο επαφής M₁ διχοτομεί τη γωνία που σχηματίζουν η ημιευθεία M₁E και η ημιευθεία M₁t , που είναι ομόρροπη της ΟΕ, όπου Ε είναι η εστία της παραβολής.

ΑΠΟΔΕΙΞΗ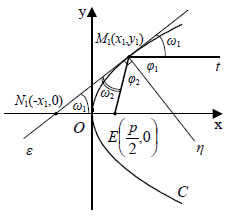

Έστω ε η εφαπτομένη της παραβολής στο M₁(x₁,y₁) και N₁ το σημείο τομής της με τον άξονα x'x . Για να δείξουμε ότι φ₁=φ₂ , αρκεί να δείξουμε ότι ω₁=ω₂ ή ισοδύναμα ότι

Πράγματι, επειδή η ε έχει εξίσωση yy₁ = p(x + x₁) , το N₁ θα έχει συντεταγμένες ( -x₁,0) , οπότε θα ισχύει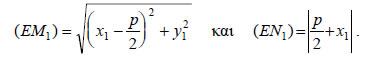

Επομένως, έχουμε: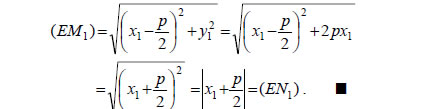

Η χρήση της παραπάνω ιδιότητας γίνεται στα παραβολικά τηλεσκόπια, στα ραντάρ, στα φανάρια των αυτοκινήτων, στους προβολείς των οδοντιάτρων κτλ. Συγκεκριμένα:

— Όλες οι ακτίνες φωτός που προσπίπτουν στο παραβολικό κάτοπτρο παράλληλα προς τον άξονά του, ανακλώμενες, συγκεντρώνονται στην εστία.

— Στα φανάρια των αυτοκινήτων που έχουν παραβολικά κάτοπτρα οι λαμπτήρες βρίσκονται στην εστία τους. Έτσι, οι φωτεινές ακτίνες, ανακλώμενες στο κάτοπτρο, εξέρχονται παράλληλα προς τον άξονά του.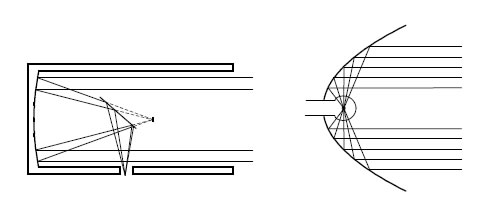

ΣΧΟΛΙΟ

Σύμφωνα με την προηγούμενη απόδειξη, για να φέρουμε την εφαπτομένη μιας παραβολής σε ένα σημείο της M₁(x₁,y₁) , αρκεί να ενώσουμε το σημείο N₁( - x₁,0) με το M₁(x₁,y₁) .

ΕΦΑΡΜΟΓΕΣ

1.Έστω η παραβολή C :y² =2px και ε₁ , ε₂ οι εφαπτόμενες της παραβολής από ένα σημείο M₀(x₀,y₀) με . Αν M₁, M₁ εί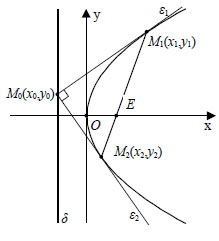ναι τα σημεία επαφής των ε₁ , ε₂ με την παραβολή C, να αποδειχτεί ότι
(i) Η ευθεία M₁M₂ έχει εξίσωση yy₀ = p(x +x₀)
(ii) Η ευθεία M₁M₂ διέρχεται από την εστία, αν και μόνο αν τοM₀ ανήκει στη διευθετούσα της παραβολής.

ΑΠΟΔΕΙΞΗ

(i) Αν (x₁,y₁) και (x₂,y₂) είναι οι συντεταγμένες των σημείων M₁ και M₂ , τότε οι εφαπτόμενες ε₁ και ε₂ θα έχουν εξισώσεις: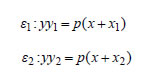

και επειδή οι ε₁ και ε₂ διέρχονται από το M₀(x₀,y₀) , θα ισχύουν

Επομένως, οι συντεταγμένες των M₁ και M₂ θα επαληθεύουν την εξίσωση

Άρα, η (1) θα είναι η εξίσωση της χορδής M₁M₂.

(ii) Λόγω της (i), η ευθεία M₁M₂ διέρχεται από την εστία 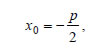, αν και μόνο αν οι συντεταγμένες της Ε επαληθεύουν την εξίσωση της , δηλαδή, αν και μόνο αν ισχύει ή ισοδύναμα

που συμβαίνει, αν και μόνο αν το σημείο M₀(x₀,y₀) ανήκει στη διευθετούσα x= - p/2 της παραβολής.

ΣΧΟΛΙΟ

Η ευθεία M₁M₂ λέγεται πολική του σημείου M₀ ως προς την παραβολή C, ενώ το σημείο M₀ λέγεται πόλος της M₁M₂ ως προς την C. Παρατηρούμε ότι η εξίσωση της πολικής ενός σημείου M₀(x₀,y₀) ως προς την παραβολή C: y²=2px έχει τη μορφή που θα είχε η εφαπτομένη της C στο σημείο M₀(x₀,y₀) , αν αυτό ανήκε στην C.

2.Έστω η παραβολή y²=2px και η εφαπτομένη της ε σε ένα σημείο της M₁(x₁,y₁) , η οποία τέμνει τη διευθετούσα της παραβολής στο σημείο M₂. Να αποδειχτεί ότι .

ΑΠΟΔΕΙΞΗ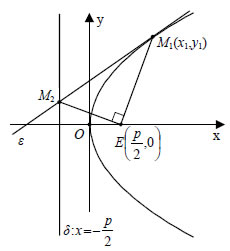

Η εξίσωση της ε είναι

Επειδή το σημείο M₁(x₁,y₁) είναι σημείο της παραβολής, ισχύει y₁²=2px₁ , οπότε 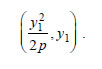. Άρα, οι συντεταγμένες του M₁ είναι

Έτσι, η εξίσωση (1) γράφεται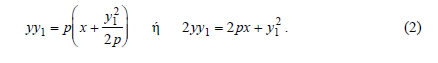

Επομένως, οι συντεταγμένες του M₂ θα είναι η λύση του συστήματος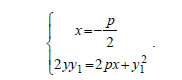

Από την επίλυση του συστήματος αυτού βρίσκουμε ότι οι συντεταγμένες του M₂ είναι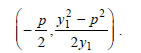

Έτσι, έχουμε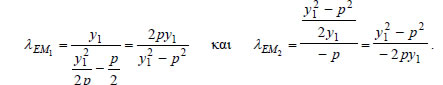

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρεθεί η εξίσωση της παραβολής που έχει κορυφή την αρχή των αξόνων και άξονα συμμετρίας τον άξονα x'x σε καθεμιά από τις παρακάτω περιπτώσεις: (i)  Όταν έχει εστία το σημείο E( -1,0) (ii) Όταν έχει διευθετούσα την ευθεία x= 1/2 (iii) Όταν διέρχεται από το σημείο A(1,2)
2.	Να βρεθεί η εστία και η διευθετούσα της παραβολής με εξίσωση:
3.	Δίνεται η παραβολή y2=2px . Να αποδειχτεί ότι η κορυφή της παραβολής είναι το πλησιέστερο στην εστία σημείο της.
4.	Να βρεθούν οι συντεταγμένες των σημείων Α και Β της παραβολής y= 1/4 x2 , που έχουν την ίδια τεταγμένη και ισχύει .
5.	Να βρεθεί η εξίσωση της εφαπτομένης της παραβολής y= 1/4 x2 σε καθεμιά από τις παρακάτω περιπτώσεις: (i) Όταν είναι παράλληλη στην ευθεία y=x+1 (ii) Όταν είναι κάθετη στην ευθεία y= -2x (iii) Όταν διέρχεται από το σημείο A(0, -1) .
6.	Να αποδείξετε ότι οι εφαπτόμενες της παραβολής y= 1/4 x2 στα σημεία A(4,4) και τέμνονται κάθετα και πάνω στη διευθετούσα της.