3.3 Η ΕΛΛΕΙΨΗ

Ορισμός Έλλειψης

Έστω Ε' και Ε δύο σημεία ενός επιπέδου. Ονομάζεται έλλειψη με εστίες τα σημεία Ε' και Ε ο γεωμετρικός τόπος C των σημείων του επιπέδου των οποίων το άθροισμα των αποστάσεων από τα Ε' και Ε είναι σταθερό και μεγαλύτερο του Ε'E . Το σταθερό αυτό άθροισμα το συμβολίζουμε, συνήθως, με 2α και την απόσταση των εστιών Ε' και Ε με 2γ. H απόσταση Ε'E ονομάζεται εστιακή απόσταση της έλλειψης.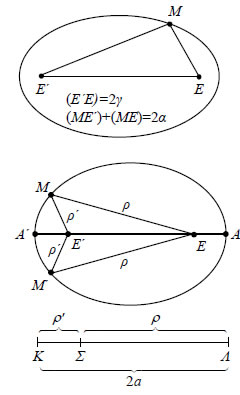

Σύμφωνα με τον παραπάνω ορισμό:

α) Ένα σημείο Μ του επιπέδου είναι σημείο της έλλειψης, αν και μόνο αν

β) Ισχύει , δηλαδή . Αν γ=0 , τότε τα σημεία Ε',E συμπίπτουν, οπότε η έλλειψη γίνεται κύκλος με κέντρο το Ε και ακτίνα α.

Για να βρούμε ένα σημείο της έλλειψης C, εργαζόμαστε ως εξής:

Παίρνουμε ένα τμήμα ΚΛ μήκους 2α και ένα οποιοδήποτε σημείο του Σ. Με κέντρα τα Ε' και Ε και ακτίνες ρ'= (ΚΣ) και ρ= (ΛΣ) , αντιστοίχως, γράφουμε δύο κύκλους, οι οποίοι τέμνονται στα σημεία Μ και M' . Τα σημεία Μ και M' είναι σημεία της έλλειψης, γιατί ισχύει .

Με τον ίδιο τρόπο μπορούμε να κατασκευάσουμε οσαδήποτε σημεία της έλλειψης.

Πρακτικά μπορούμε να σχεδιάσουμε την έλλειψη ως εξής: Παίρνουμε ένα σχοινί μήκους 2α και στερεώνουμε τα άκρα του στις εστίες Ε' και Ε. Αν τώρα με ένα μολύβι διατηρούμε το σχοινί τεντωμένο, τότε αυτό, κατά την κίνησή του, θα διαγράψει την έλλειψη.

Εξίσωση Έλλειψης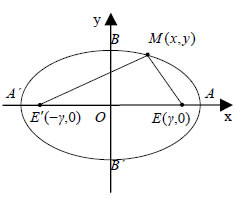

• Έστω μια έλλειψη C με εστίες Ε' και Ε. Θα βρούμε την εξίσωση της έλλειψης ως προς σύστημα συντεταγμένων Oxy με άξονα των x την ευθεία Ε'E και άξονα των y τη μεσοκάθετο του Ε'E .

Αν M(x,y) είναι ένα σημείο της έλλειψης C, τότε θα ισχύει

Επειδή (E'E)=2γ , οι εστίες Ε' και Ε θα έχουν συντεταγμένες (-γ,0) και (γ,0) αντιστοίχως. Επομένως,

Έτσι, η σχέση (1) γράφεται

από την οποία έχουμε διαδοχικά: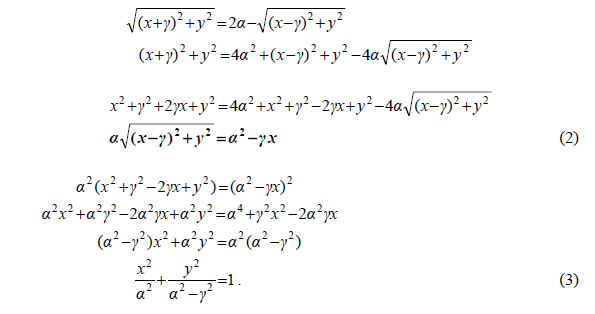

Επειδή 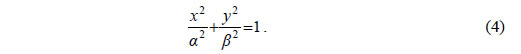, οπότε αν θέσουμε , η εξίσωση (3) παίρνει τη μορφή

Αποδεικνύεται και το αντίστροφο, δηλαδή ότι κάθε σημείο M(x,y) , του οποίου οι συντεταγμένες επαληθεύουν την εξίσωση (4), είναι σημείο της έλλειψης C.Επομένως, η εξίσωση της έλλειψης C με εστίες τα σημεία E'( -γ,0), Ε(γ,0) , και σταθερό άθροισμα 2α είναι

Για παράδειγμα, η εξίσωση της έλλειψης με εστίες τα σημεία E'( -4,0) , E(4,0) και σταθερό άθροισμα 2α=10 είναι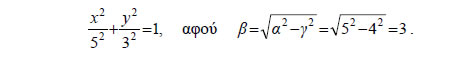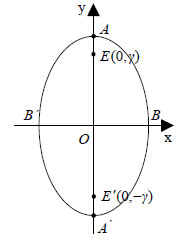

• Αν τώρα πάρουμε σύστημα συντεταγμένων Oxy με άξονα των x τη μεσοκάθετο του E'E και άξονα των y την ευθεία E'E και εργαστούμε όπως πριν, θα βρούμε ότι η εξίσωση της έλλειψης C είναι

Για παράδειγμα, η έλλειψη με εστίες E'(0, -4) , E(0,4) και σταθερό άθροισμα 2α=10 είναι

Ιδιότητες Έλλειψης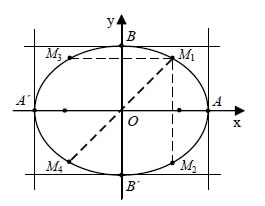

Έστω μια έλλειψη

• Αν M₁(x₁,y₁) είναι ένα σημείο της έλλειψης C, τότε τα σημεία M₂(x₁, -y₁) , M₃( -x₁,y₁) και M₄( -x₁, -y₁) ανήκουν στην C, αφού οι συντεταγμένες τους επαληθεύουν την εξίσωσή της. Αυτό

σημαίνει ότι η παραπάνω έλλειψη έχει τους άξονες x'x και y'y άξονες συμμετρίας και την αρχή των αξόνων κέντρο συμμετρίας. Επομένως, η ευθεία που ενώνει τις εστίες E',E της έλλειψης και η μεσοκάθετος του E'E είναι άξονες συμμετρίας της έλλειψης, ενώ το μέσο Ο του E'E είναι κέντρο συμμετρίας της. Το σημείο Ο λέγεται κέντρο της έλλειψης.

• Από την εξίσωση της έλλειψης για y=0 βρίσκουμε , ενώ για x=0 βρίσκουμε . Επομένως, η έλλειψη C τέμνει τον άξονα x'x στα σημεία A'(-α,0) και Α(α,0) , ενώ τον άξονα y'y στα σημεία Β'(0,-β) και B(0,β). Τα σημεία A',A,B',B λέγονται κορυφές της έλλειψης, ενώ τα ευθύγραμμα τμήματα A'A και B'B, τα οποία έχουν μήκη (A'A)=2α και (B'B)=2β, λέγονται μεγάλος άξονας και μικρός άξονας αντιστοίχως. Το ευθύγραμμο τμήμα που ορίζουν δύο οποιαδήποτε συμμετρικά ως προς Ο σημεία M₁ και M₄ της έλλειψης λέγεται διάμετρος της έλλειψης. Αποδεικνύεται ότι

δηλαδή ότι κάθε διάμετρος της έλλειψης είναι μεγαλύτερη ή ίση από το μικρό άξονα και μικρότερη ή ίση από το μεγάλο άξονα της έλλειψης.

• Τέλος, από την εξίσωση της έλλειψης, έχουμε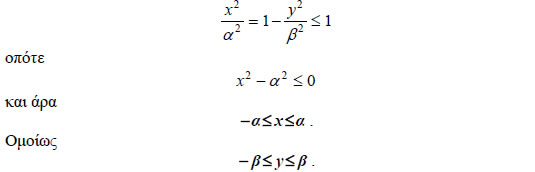

Άρα, η έλλειψη περιέχεται στο ορθογώνιο που ορίζουν οι ευθείες x= -α, x=α και y= -β, y= β.

Εκκεντρότητα Έλλειψης

Μια παράμετρος που καθορίζει τη μορφή της έλλειψης είναι η εκκεντρότητα της έλλειψης. Ονομάζουμε εκκεντρότητα της έλλειψης Εικόνα και τη

συμβολίζουμε με ε, το λόγο 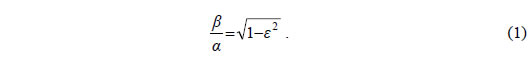Εικόνα οπότε και άρα

Επομένως, όσο μεγαλώνει η εκκεντρότητα τόσο μικραίνει ο λόγος β/α και κατά συνέπεια τόσο πιο επιμήκης γίνεται η έλλειψη (Σχ. α).

Όταν το ε τείνει στο μηδέν, τότε ο λόγος β/α τείνει στο 1 και επομένως η έλλειψη τείνει να γίνει κύκλος. Όταν, όμως, το ε τείνει στη μονάδα, τότε ο λόγος β/α τείνει στο 0 και επομένως η έλλειψη τείνει να εκφυλιστεί σε ευθύγραμμο τμήμα.

Οι ελλείψεις που έχουν την ίδια εκκεντρότητα, άρα ίδιο λόγο β/α, λέγονται όμοιες (Σχ. β).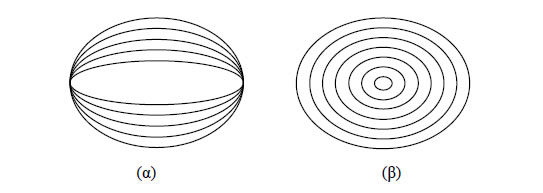

Είναι γνωστό από την Αστρονομία ότι οι τροχιές των πλανητών γύρω από τον Ήλιο είναι ελλείψεις, των οποίων τη μία εστία κατέχει ο Ήλιος. Οι εκκεντρότητες των τροχιών αυτών είναι οι εξής: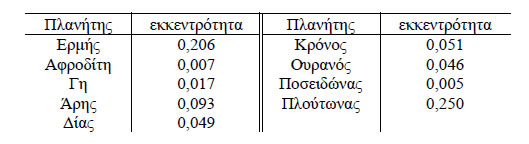

Παραμετρικής Εξισώσεις Έλλειψης

Έστω η έλλειψη Εικόνα και ένα σημείο M(x,y) του καρτεσιανού επιπέδου.

— Αν το M(x,y) ανήκει στην έλλειψη C, τότε θα ισχύει 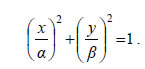, οπότε θα έχουμε

Επομένως, το σημείο Εικόνα θα ανήκει στο μοναδιαίο κύκλο, οπότε θα υπάρχει γωνία φε[0,2π), τέτοια, ώστε, δηλαδή

— Αντιστρόφως, αν ισχύουν οι (1) για κάποια γωνία φε[0,2π), τότε το σημείο M(x,y) θα ανήκει στην έλλειψη C, αφού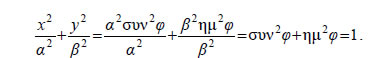

Επομένως, οι συντεταγμένες των σημείων M(x,y) της έλλειψης C και μόνο αυτές ικανοποιούν τις εξισώσεις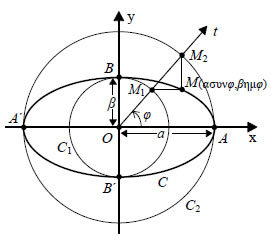

Οι εξισώσεις αυτές λέγονται παραμετρικές εξισώσεις της έλλειψης C. Σύμφωνα με τις παραμετρικές εξισώσεις το σημείο M(ασυνφ,βημφ) της έλλειψης προσδιορίζεται ως εξής:

Γράφουμε τους κύκλους C₁ και C₂ με κέντρο Ο και ακτίνες β και α αντιστοίχως και φέρνουμε μια ημιευθεία Ot , έτσι ώστε . Αν η ημιευθεία Ot τέμνει τους C₁ και C₂ στα σημεία M₁ και M₂

αντιστοίχως και οι παράλληλες από τα M₁,M₂ προς τους άξονες x'x , y'y , αντιστοίχως, τέμνονται στο σημείο Μ, τότε το Μ θα ανήκει στην έλλειψη C. Πράγματι, το σημείο M₁ θα έχει συντεταγμένες (βσυνφ,βημφ), ενώ το M₂ θα έχει συντεταγμένες (ασυνφ,αημφ) . Άρα, οι συντεταγμένες του Μ θα είναι (ασυνφ,βημφ) .

ΕΦΑΡΜΟΓΕΣ

Έστω ο κύκλος x² +y² =α², α>0 και ένα σημείο του M₁ , του οποίου η ορθή προβολή στον άξονα x'x είναι το σημείο M₂. Πάνω στο ευθύγραμμο τμήμα M₁M₂ ορίζουμε ένα σημείο Μ, τέτοιο, ώστε να ισχύει . Να αποδει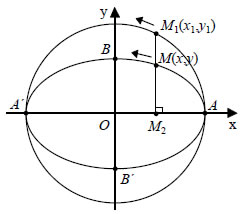χτεί ότι αν το M₁ κινείται στον κύκλο, το Μ κινείται στην έλλειψη .

ΑΠΟΔΕΙΞΗ

Έστω (x₁,y₁) οι συντεταγμένες του M₁ και (x,y) οι συντεταγμένες του Μ. Επειδή , οπότε

Επειδή, επιπλέον η M₁M₂ είναι κάθετη στον άξονα x'x θα ισχύει

Όμως, το σημείο M₁(x₁,y₁) ανήκει στον κύκλο x² +y² = a² . Επομένως, ισχύει x₁² +y₁² = a² , οπότε, λόγω των σχέσεων (1) και (2), έχουμε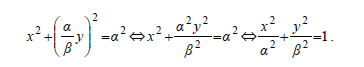

Άρα, το σημείο M(x,y) ανήκει στην έλλειψη .

Εφαπτομένη Έλλειψης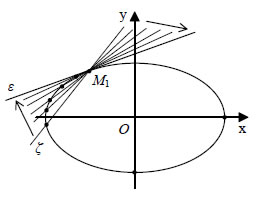

• Έστω μια έλλειψη C με εξίσωση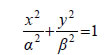

και ένα σημείο της M₁(x₁,y₁). Η εφαπτομένη της έλλειψης C στο σημείο M₁(x₁,y₁) ορίζεται με τρόπο ανάλογο προς εκείνο με τον οποίο ορίστηκε η εφαπτομένη της παραβολής και αποδεικνύεται ότι έχει εξίσωση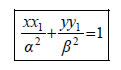

Για παράδειγμα, η εφαπτομένη της έλλειψης στο σημείο της , η οποία γράφεται ισοδύναμα .

• Αν μια έλλειψη έχει εξίσωση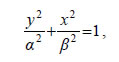

τότε η εφαπτομένη της στο σημείο M₁(x₁,y₁) έχει εξίσωση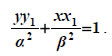

• Όπως η παραβολή έτσι και η έλλειψη έχει ανάλογη ανακλαστική ιδιότητα. Συγκεκριμένα:

Η κάθετη στην εφαπτομένη μιας έλλειψης στο σημείο επαφής Μ διχοτομεί τη γωνία , όπου E',E οι εστίες της έλλειψης.

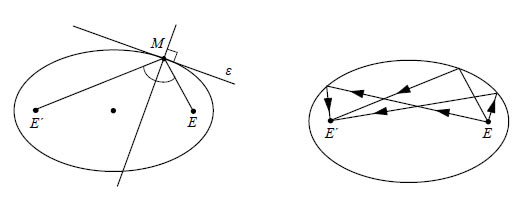Σύμφωνα με την ιδιότητα αυτή ένα ηχητικό κύμα ή μια φωτεινή ακτίνα που ξεκινούν από τη μία εστία μιας έλλειψης, ανακλώμενα σε αυτήν, διέρχονται από την άλλη εστία.

Η ιδιότητα αυτή χρησιμοποιείται στο σχεδιασμό ορισμένων τύπων οπτικών οργάνων και στην κατασκευή των λεγόμενων "στοών με ειδική ακουστική". Οι στοές αυτές είναι αίθουσες με ελλειπτική οροφή, στις οποίες ένα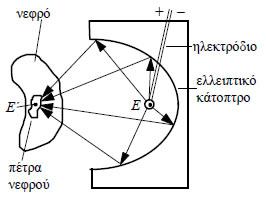

πρόσωπο που ψιθυρίζει στη μια εστία μπορεί να ακουστεί στην άλλη εστία. Ακόμη, η ανακλαστική ιδιότητα της έλλειψης βρίσκει σπουδαία εφαρμογή σε μια ιατρική μέθοδο που λέγεται λιθοθρυψία. Η μέθοδος αυτή εφαρμόζεται ως εξής: Στη μια εστία της έλλειψης τοποθετείται ένα ηλεκτρόδιο εκπομπής υπερήχων, ενώ ο ασθενής τοποθετείται σε τέτοια θέση, ώστε το νεφρό του να είναι στην άλλη εστία. Τότε οι πέτρες του νεφρού κονιορτοποιούνται από τους ανακλώμενους υπερήχους.

ΕΦΑΡΜΟΓΕΣ

1. Δίνονται η έλλειψη . Αν M₁(x₁ , y₁) είναι ένα σημείο της C₁ και M₂(x₂ , y₂) το σημείο του C₂ με x₂ = x₁ , να αποδειχτεί ότι η εφαπτομένη ε₁ της έλλειψης C₁ στο σημείο M₁ και η εφαπτομένη ε₂ του κύκλου C₂στο σημείο M₂ τέμνονται πάνω στον άξονα x'x.

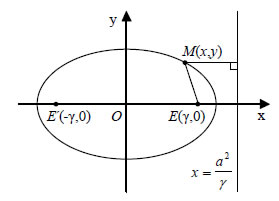
ΑΠΟΔΕΙΞΗ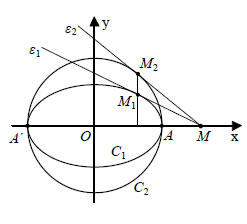

Η εξίσωση της ε₁ είναι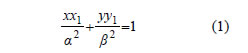

και της ε₂ είναι

Για y=0, από την (1) βρίσκουμε , ενώ από τη (2) βρίσκουμε . Άρα, και η ε₁ και η ε₂ τέμνουν τον x'x στο ίδιο σημείο, το Εικόνα .

ΣΧΟΛΙΟ

Σύμφωνα με την εφαρμογή αυτή, για να φέρουμε την εφαπτομένη ε₁ της έλλειψης C₁ στο σημείο M₁ , φέρνουμε την εφαπτομένη ε₂ του κύκλου C₂ στο σημείο M₂ και στη συνέχεια ενώνουμε το σημείο τομής Μ των ε₂ και x'x με το σημείο M₁. Η MM₁ είναι η ζητούμενη εφαπτομένη.

2. Έστω C η έλλειψη με εστίες τα σημεία E'( -γ,0) και E( γ,0) και μεγάλο άξονα 2α . Να αποδειχτεί ότι ο λόγος των αποστάσεων οποιουδήποτε σημείου M(x,y) της έλλειψης από την εστία E(γ,0) και την ευθεία είναι σταθερός και ίσος με την εκκεντρότητα της έλλειψης. Ομοίως, για την εστία E'( -γ,0) και την ευθεία .

ΑΠΟΔΕΙΞΗ

Επειδή το M(x,y) ανήκει στην έλλειψη C, θα ισχύει

Επομένως, όπως είδαμε στην απόδειξη της εξίσωσης της έλλειψης, θα έχουμε

Η ισότητα αυτή γράφεται διαδοχικά: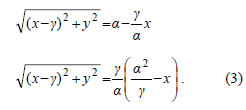

Όμως,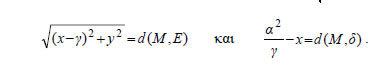

Επομένως, η (3) γράφεται

ή ισοδύναμα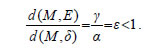

Ασκήσεις

Α' ΟΜΑΔΑΣ

Να βρείτε την εξίσωση της έλλειψης σε καθεμιά από τις παρακάτω περιπτώσεις:

(i) Όταν έχει εστίες τα σημεία E'(-4,0) και E(4,0) και μεγάλο άξονα 10

(ii) Όταν έχει εστίες τα σημεία E'(0, -5) και E(0,5) και μεγάλο άξονα 26

(iii) Όταν έχει εστίες τα σημεία E'( -12, 0) καιE(12, 0) και εκκεντρότητα 12/13

(iv) Όταν έχει εστίες τα σημεία E'(-4,0) και E(4,0) και διέρχεται από το σημείο M(4,9/5)

(v) Όταν έχει εστίες στον άξονα y'y και διέρχεται από τα σημεία M₁(1,1) και M₂(2,1/2) .

Να βρείτε τα μήκη των αξόνων, τις εστίες και την εκκεντρότητα των ελλείψεων:

3.	Να εγγράψετε στην έλλειψη 4x² +y²=4 τετράγωνο με πλευρές παράλληλες προς τους άξονες.
4.	Αν E', E είναι οι εστίες και B'B ο μικρός άξονας της έλλειψης x² +2y²=4 , να αποδείξετε ότι το τετράπλευρο EBB'E' είναι τετράγωνο.
5.	Να αποδείξετε ότι οι εφαπτόμενες μιας έλλειψης στα άκρα μιας διαμέτρου της είναι παράλληλες. (Διάμετρος μιας έλλειψης λέγεται το τμήμα που συνδέει δύο σημεία της έλλειψης και διέρχεται από την αρχή των αξόνων).
6.	Να βρεθούν οι εξισώσεις των εφαπτομένων της έλλειψης 3x² +y²=4, οι οποίες: (i) είναι παράλληλες προς την ευθεία y= -3x+1 (ii) είναι κάθετες στην ευθεία y= 1/2x (iii) διέρχονται από το σημείο M(0,4) .
7.	Να αποδείξετε ότι οι εφαπτόμενες της έλλειψης x²+ 4y²=100 στα σημεία της σχηματίζουν τετράγωνο με διαγώνιες τους άξονες x'x και y'y .

Β' ΟΜΑΔΑΣ
1.	Να αποδείξετε ότι το σημείο ανήκει στην έλλειψη για όλες τις τιμές του .
2.	Να αποδείξετε ότι το σημείο τομής των ευθειών ανήκει στην έλλειψη για όλες τις τιμές του .
3.	Αν M(x,y) είναι ένα σημείο της έλλειψης , να αποδείξετε ότι
4.	Αν d,d' είναι οι αποστάσεις των σημείων Γ(0,γ) και Γ'(0, -γ) από την εφαπτομένη της έλλειψης σε ένα σημείο της M(x,y), να αποδείξετε ότι.

5	Έστω Μ₁(x₁,y₁) , Μ₂(x₂,y₂) δύο σημεία της έλλειψης και τα σημεία N₁(εx₁,0) και N₂(εx₂,0) . Να αποδείξετε ότι (M₁N₂)=(M₂N₁).
6.	Έστω η έλλειψη και ένα σημείο της Μ. Έστω επιπλέον, ο κύκλος x²+y²=α² και το σημείο του Ν, που έχει την ίδια τετμημένη με το Μ. Από το Μ φέρνουμε παράλληλη προς την ON , που τέμνει τους άξονες x'x και y'y στα σημεία Γ και Δ αντιστοίχως. Να αποδείξετε ότι ΜΓ=β και ΜΔ=α .
7.	Έστω ε και ε' οι εφαπτόμενες της έλλειψης C :, στις κορυφές της A(α,0) και Α'(−α,0) , αντιστοίχως, και ζ η εφαπτομένη της C σε ένα σημείο της Μ₁(x₁,y₁). Αν η ζ τέμνει τις ε και ε' στα σημεία Γ και Γ' , αντιστοίχως, να αποδείξετε ότι: (i) (ΑΓ)(Α'Γ')=β² (ii) ο κύκλος με διάμετρο το ΓΓ' διέρχεται από τις εστίες της έλλειψης.
8.	Έστω η έλλειψη και η εφαπτομένη στο σημείο της Μ₁(x₁,y₁). Αν η εφαπτομένη τέμνει τους άξονες x'x και y'y στα σημεία Γ(p,0) και Δ(0,q) ,να αποδείξετε ότι .