3ΚΩΝΙΚΕΣ ΤΟΜΕΣ

Εισαγωγή

Η μελέτη της έλλειψης, της παραβολής και της υπερβολής από τους Αρχαίους Έλληνες μαθηματικούς φαίνεται ότι είχε αφετηρία τη σχέση αυτών των καμπύλων με ορισμένα προβλήματα γεωμετρικών κατασκευών, όπως, για παράδειγμα, το περίφημο πρόβλημα διπλασιασμού του κύβου:

"Δοθέντος ενός κύβου, να κατασκευαστεί ένας άλλος με διπλάσιο όγκο".

Με αλγεβρικό συμβολισμό αυτό σημαίνει ότι αν α είναι η πλευρά του αρχικού κύβου, να κατασκευαστεί ένα ευθύγραμμο τμήμα x , που θα είναι η πλευρά του κύβου με όγκο 2a³ , δηλαδή x³ = 2a³ . Ο Πρόκλος (450 περίπου μ.Χ.) αναφέρει ότι ο Ιπποκράτης ο Χίος (430 περίπου π.Χ.) ήταν ο πρώτος που ανήγαγε το πρόβλημα διπλασιασμού του κύβου στην παρεμβολή δύο μέσων αναλόγων ανάμεσα στο α και το 2α, δηλαδή στην κατασκευή δύο τμημάτων x και y, τέτοιων, ώστε (από τις αναλογίες αυτές προκύπτει εύκολα ότι x³ = 2a³ , δηλαδή το x θα είναι η πλευρά του ζητούμενου κύβου).

Υπενθυμίζουμε εδώ ότι το πρόβλημα παρεμβολής μιας μέσης αναλόγου ανάμεσα σε δύο γνωστά τμήματα α, β (δηλαδή η κατασκευή τμήματος x τέτοιου, ώστε a/x=x/β ) λύνεται εύκολα με κανόνα και διαβήτη, δηλαδή με τη βοήθεια ευθείας και κύκλου. Δεν ισχύει όμως το ίδιο για την παρεμβολή δύο μέσων αναλόγων η οποία απαιτεί τη χρησιμοποίηση διαφορετικών γεωμετρικών καμπύλων. Επειδή από τις αναλογίες (1) προκύπτει x²=αy (2), y²=2αx(3) και xy=2a² ή y=2a²/x (4), συμπεραίνουμε ότι τα μήκη των τμημάτων x και y θα είναι οι συντεταγμένες του σημείου τομής δύο από τις τρεις καμπύλες (2), (3) και (4), που είναι αντιστοίχως δύο παραβολές και μία υπερβολή.

Η φράση "Μεναιχμείους κωνοτομείν τριάδας", που αναφέρεται σε ένα επίγραμμα του Ερατοσθένη του Κυρηναίου (250 περίπου π.Χ.) σχετικό με το διπλασιασμό του κύβου, έχει οδηγήσει στην υπόθεση ότι οι τρεις αυτές

καμπύλες ανακαλύφθηκαν από τον Μέναιχμο, εταίρο στην Ακαδημία του Πλάτωνα, γύρω στο 350 π.Χ.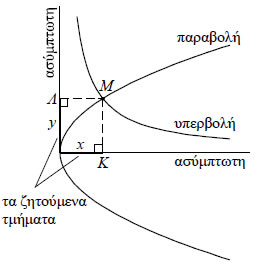

Στη μία από τις δύο λύσεις του Μέναιχμου, που αναφέρει ο Ευτόκιος ο Ασκαλωνίτης (550 περίπου μ.Χ.), οι καμπύλες κατασκευάζονται σύμφωνα με τα γεωμετρικά ισοδύναμα των (3) και (4). Για παράδειγμα, το Μ, ως σημείο της παραβολής, προσδιορίζεται, έτσι ώστε το τετράγωνο πλευράς ΜΚ να είναι ισοδύναμο προς ένα ορθογώνιο με πλευρές 2α και ΜΛ (δηλαδή y²=2αx ), ενώ ως σημείο της υπερβολής, έτσι ώστε το ορθογώνιο με πλευρές ΜΛ και ΜΚ να είναι ισοδύναμο προς ένα ορθογώνιο με πλευρές 2α και α (δηλαδή xy = 2a²) . Τέλος, τα ζητούμενα τμήματα x, y προσδιορίζονται φέρνοντας τις κάθετες από το σημείο τομής των δύο καμπύλων πάνω στις ασύμπτωτες της υπερβολής (η μία από τις οποίες είναι ταυτόχρονα και άξονας συμμετρίας της παραβολής).

Γύρω στο 300 π.Χ., η υπερβολή, η παραβολή και η έλλειψη είχαν γίνει αντικείμενο συστηματικής μελέτης, ως οι τομές που δημιουργούνται στην επιφάνεια ενός κώνου από ένα επίπεδο κάθετο σε μια γενέτειρά του.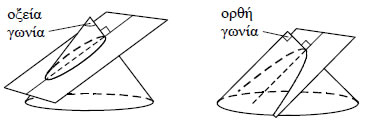

Ανάλογα με τη γωνία της κορυφής του κώνου οι καμπύλες αυτές ορίζονταν ως "οξυγωνίου κώνου τομή" (έλλειψη), "ορθογωνίου κώνου τομή" (παραβολή) και "αμβλυγωνίου κώνου τομή" (υπερβολή). Οι όροι αυτοί χρησιμοποιούνται από τον Αρχιμήδη (287-212 π.Χ.) στα έργα του "Τετραγωνισμός ορθογωνίου κώνου τομής" και "Περί κωνοειδέων και σφαιροειδέων". Αποκορύφωμα της θεωρητικής μελέτης των τριών κωνικών τομών κατά την αρχαιότητα, υπήρξε το περίφημο έργο "Κωνικά" του Απολλώνιου του Περγαίου (250 περίπου π.Χ.), ο οποίος στηρίχτηκε σε προηγούμενα έργα του Αρισταίου και του Ευκλείδη, τα οποία όμως δε διασώθηκαν.

Τα "Κωνικά" ήταν χωρισμένα σε 8 βιβλία, που περιείχαν μια άψογη γεωμετρική θεωρία των κωνικών τομών και ένα μεγάλο πλήθος νέων αποτελε-σμάτων. Στα 7 πρώτα βιβλία που έχουν διασωθεί υπάρχουν 387 θεωρήματα ενώ στο 8ο, όπως συνάγεται από μαρτυρία του Πάππου, υπήρχαν άλλα 100.

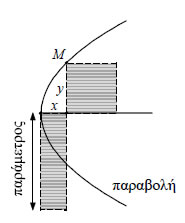Μια βασική καινοτομία του Απολλώνιου υπήρξε ο ορισμός των τριών καμπύλων διαμέσου τριών διαφορετικών τομών ενός κώνου, καθώς και η εισαγωγή των όρων "παραβολή", "έλλειψη" και "υπερβολή".

Τα ονόματα αυτά έχουν άμεση σχέση με το νέο τρόπο ορισμού των κωνικών τομών από τον Απολλώνιο, σύμφωνα με τον οποίο, σε κάθε τομή του κώνου από το επίπεδο αντιστοιχεί ένα σταθερό μήκος (παράμετρος), το οποίο εξαρτάται από το είδος του κώνου και από τη θέση του επιπέδου. Ο Απολλώνιος έδειξε ότι για κάθε καμπύλη τα δύο γραμμοσκιασμένα εμβαδά σε καθένα από τα διπλανά σχήματα είναι ίσα μεταξύ τους. Το ένα από αυτά είναι το τετράγωνο με πλευρά την κάθετη από σημείο της καμπύλης προς τον άξονα συμμετρίας της. το άλλο είναι ένα ορθογώνιο με μια πλευρά την απόσταση του ίχνους αυτής της κάθετης από την κορυφή της καμπύλης. Η σχέση της άλλης πλευράς του ορθογωνίου προς τη σταθερή παράμετρο της τομής είναι αυτή που καθορίζει τη μορφή και το όνομα της καμπύλης. Αν η άλλη πλευρά ισούται ("παραβάλλεται") προς την παράμετρο, τότε η καμπύλη είναι παραβολή. Αν η άλλη πλευρά είναι μικρότερη ("ελλείπει") από την παράμετρο, η καμπύλη είναι έλλειψη, ενώ αν είναι μεγαλύτερη ("υπερβάλλει"), η καμπύλη είναι υπερβολή.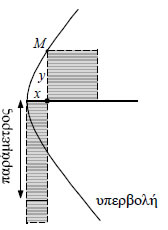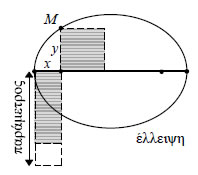

3.1 Ο ΚΥΚΛΟΣ

Εξίσωση Κύκλου

Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και C ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ. Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x,y) ανήκει στον κύκλο C, αν και μόνο αν απέχει από το κέντρο του Ο απόσταση ίση με ρ, δηλαδή, αν και μόνο αν ισχύει:

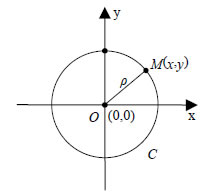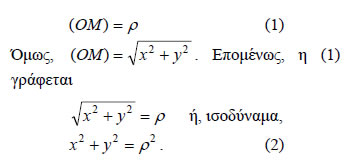Παρατηρούμε, δηλαδή, ότι οι συντεταγμένες των σημείων του κύκλου και μόνο αυτές επαληθεύουν την εξίσωση (2). Άρα, ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ έχει εξίσωση

Για παράδειγμα, ο κύκλος με κέντρο το σημείο Ο(0,0) και ακτίνα ρ=1 έχει εξίσωση x² + y² =1 . Ο κύκλος αυτός λέγεται μοναδιαίος κύκλος.

Παραμετρικές Εξισώσεις Κύκλου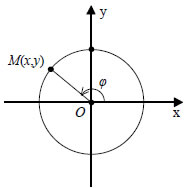

Έστω ο κύκλος C: x² + y ² = ρ² και ένα σημείο M(x,y) του καρτεσιανού επιπέδου.

Αν το M(x,y) ανήκει στον κύκλο C και είναι η γωνία που σχηματίζει το διάνυσμα με τον άξονα x'x , τότε, όπως γνωρίζουμε από την Τριγωνομετρία, θα ισχύουν οι σχέσεις:

Αντιστρόφως, αν για τις συντεταγμένες x,y του Μ ισχύουν οι σχέσεις (1), τότε το σημείο Μ θα ανήκει στον κύκλο C, αφού

Επομένως, οι συντεταγμένες των σημείων M(x,y) του κύκλου C και μόνον αυτές ικανοποιούν τις εξισώσεις

Οι εξισώσεις αυτές λέγονται παραμετρικές εξισώσεις του κύκλου C.

Εφαπτομένη Κύκλου

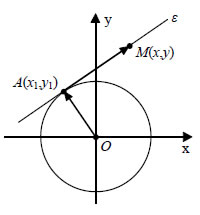Έστω ε η εφαπτομένη του κύκλου C: x² + y ² = ρ² σε ένα σημείο του A(x₁,y₁) .Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x,y) ανήκει στην ε, αν και μόνο αν 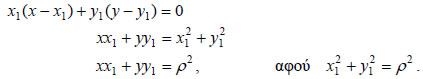, δηλαδή, αν και μόνο αν ισχύει

Όμως . Έτσι η (1) γράφεται διαδοχικά

Επομένως, η εφαπτομένη του κύκλου x² + y ² = ρ² στο σημείο του A(x₁,y₁) έχει εξίσωση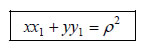

Για παράδειγμα, η εφαπτομένη του κύκλου x² + y² =1 στο σημείο έχει εξίσωση , η οποία γράφεται .

Η Εξίσωση X² + y² + Ax +By + Γ =0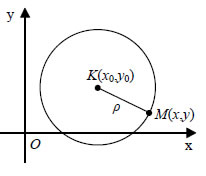

• Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και C ο κύκλος με κέντρο K(x₀,y₀) και ακτίνα ρ. Ένα σημείο M(x,y) ανήκει στον κύκλο C, αν και μόνο αν απέχει από το κέντρο του Κ απόσταση ίση με ρ, δηλαδή, αν και μόνο αν ισχύει

Όμως, .

Επομένως, η σχέση (1) γράφεται:

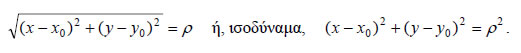
Άρα, ο κύκλος με κέντρο K(x₀,y₀) και ακτίνα ρ έχει εξίσωση:

Έτσι, για παράδειγμα, ο κύκλος με κέντρο K(1, -3) και ακτίνα ρ=2 έχει εξίσωση (x - 1)² + (y + 3)² = ρ² .

• Αν τώρα εκτελέσουμε τις πράξεις, η εξίσωση (2) γράφεται

δηλαδή παίρνει τη μορφή

όπου .

Αντιστρόφως, κάθε εξίσωση της μορφής (3) γράφεται διαδοχικά: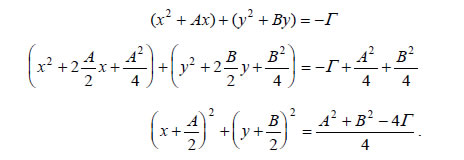

Επομένως:

- Αν , η εξίσωση (3) παριστάνει κύκλο με κέντρο και ακτίνα .

- Αν , η εξίσωση (3) παριστάνει ένα μόνο σημείο, το .

- Αν , η εξίσωση (3) είναι αδύνατη, δηλαδή δεν υπάρχουν σημεία M(x,y) των οποίων οι συντεταγμένες να την επαληθεύουν.
Αποδείξαμε λοιπόν ότι:

Κάθε κύκλος έχει εξίσωση της μορφής



και αντισ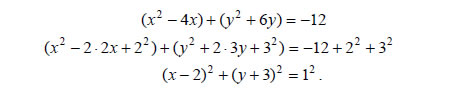τρόφως κάθε εξίσωση της μορφής (Ι) παριστάνει κύκλο.

Η εξίσωση , για παράδειγμα, γράφεται διαδοχικά

Άρα, παριστάνει κύκλο με κέντρο K(2, -3) και ακτίνα ρ=1 .

ΕΦΑΡΜΟΓΕΣ

1. Να βρεθούν οι εξισώσεις των εφαπτομένων του κύκλου C : x² + y² = 5 που διέρχονται από το σημείο A(3,1) , και να αποδειχτεί ότι οι εφαπτόμενες αυτές είναι κάθετες.

ΛΥΣΗ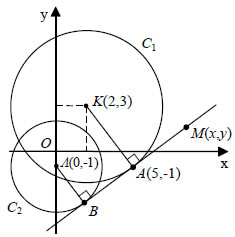

Έστω ε₁ μια εφαπτομένη του κύκλου C που διέρχεται από το σημείο Α. Αν M₁(x₁,y₁) είναι το σημείο επαφής, τότε η ε₁ θα έχει εξίσωση

και επειδή διέρχεται από το σημείο A(3,1) , θα ισχύει

Όμως, το σημείο M₁(x₁,y₁) ανήκει στον κύκλο C. Άρα, θα ισχύει

Επομένως, οι συντεταγμένες (x₁,y₁) του M₁ είναι η λύση του συστήματος των εξισώσεων (2) και (3). Λύνουμε το σύστημα αυτό και βρίσκουμε δύο λύσεις:

Άρα, υπάρχουν δύο εφαπτόμενες του C που διέρχονται από το σημείο A(3,1) , οι οποίες, λόγω των (1) και (4), έχουν εξισώσεις:

Επειδή οι συντελεστές διεύθυνσης των ε₁ και ε₂ είναι λ₁= - 1/2 και λ₂=2 , οι ευθείες ε₁ και ε₂ είναι κάθετες.

2. Δίνονται οι κύκλοι .

(i) Να βρεθεί η εξίσωση της εφαπτομένης ε του κύκλου C₁ στο σημείο A(5, -1) .

(ii) Να αποδειχτεί ότι η ε εφάπτεται και του κύκλου C₂ .

ΛΥΣΗ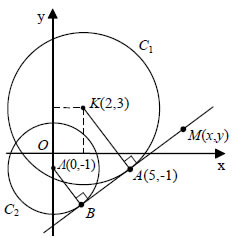

Ο κύκλος C₁ έχει κέντρο K(2,3) και ακτίνα 5, ενώ ο κύκλος C₂ έχει κέντρο Λ(0, -1) και ακτίνα 3.

(i) Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x,y) ανήκει στην ε, αν και μόνο αν , δηλαδή, αν και μόνο αν

Όμως, .

Έτσι, η (1) γράφεται διαδοχικά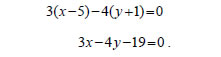

Άρα, η εξίσωση της ε είναι:

(ii) Για να δείξουμε ότι η ε εφάπτεται του κύκλου C₂ , αρκεί να δείξουμε ότι η απόσταση του κέντρου Λ(0, -1) του C₂ από την ε είναι ίση με την ακτίνα του C₂ , δηλαδή ίση με 3.

Έχουμε λοιπόν: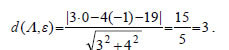

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε την εξίσωση του κύκλου με κέντρο την αρχή των αξόνων σε καθεμιά από τις παρακάτω περιπτώσεις: (i)   Όταν διέρχεται από το σημείο . (ii)   Όταν διέρχεται από το σημείο A(α - β, α + β) (iii)  Όταν εφάπτεται της ευθείας x - y=2 . (iv) Όταν εφάπτεται της ευθείας ax + βy= α2 + β2
2.	Να βρείτε την εξίσωση της εφαπτομένης του κύκλου x2 + y2 = 5 σε καθεμιά από τις παρακάτω περιπτώσεις: (i)   Όταν είναι παράλληλη στην ευθεία y= 2x +3 (ii) Όταν είναι κάθετη στην ευθεία y = 1/2 x (iii) Όταν διέρχεται από το σημείο A(5,0)
3.	Να αποδείξετε ότι οι εφαπτόμενες του κύκλου x2 + y2 = 2 στα σημεία A(1,1) ,B( -1,1) , Γ( -1, -1) και Δ(1, -1) σχηματίζουν τετράγωνο με διαγώνιες τους άξονες xx' και y'y . Ποιο είναι το εμβαδόν του τετραγώνου αυτού;
4.	Να βρείτε την εξίσωση της χορδής του κύκλου x2 + y2 = 4 που έχει μέσο το σημείο M(1, -1) .
5.	Να βρείτε την εξίσωση του κύκλου σε καθεμιά από τις παρακάτω περιπτώσεις: (i)   Όταν έχει κέντρο K(0,1) και διέρχεται από το σημείο (ii)   Όταν έχει διάμετρο το τμήμα με άκρα A( -1, 2) και B(7,8) (iii)  Όταν έχει ακτίνα ρ=5 και τέμνει τον άξονα x'x στα σημεία A(1,0) και B(7,0) (iv) Όταν διέρχεται από τα σημεία A(4,0) και B(8,0) και έχει το κέντρο του στην ευθεία y = x. (v) Όταν τέμνει τον άξονα x'x στα σημεία A(4,0) και B(8,0) και τον άξονα y'y στα σημεία Γ(0, -2) και Δ(0,μ). (vi) Όταν εφάπτεται του άξονα x'x στο σημείο A(3,0) και διέρχεται από το σημείο B(1,2) . (vii) Όταν διέρχεται από την αρχή των αξόνων και εφάπτεται της ευθείας 3x +4y=12 στο σημείο A(0,3).
6.	Να βρείτε το κέντρο και η ακτίνα του κύκλου που έχει εξίσωση