1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ

Άξονας

Πάνω σε μια ευθεία επιλέγουμε δύο σημεία O και I, έτσι ώστε το διάνυσμα να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία Ox. Λέμε τότε ότι έχουμε έναν άξονα με αρχή το Ο και μοναδιαίο διάνυσμα το καιτον συμβολίζουμε με x'x. Η ημιευθεία Ox λέγεται θετικός ημιάξονας Ox, ενώ η Ox' λέγεται αρνητικός ημιάξονας Ox'.

Αν, τώρα, πάνω στον άξονα πάρουμε ένα σημείο Μ, επειδή θα υπάρχει ακριβώς ένας πραγματικός αριθμός x τέτοιος ώστε Τον

αριθμό x τον ονομάζουμε τετμημένη του Μ. Αλλά και αντιστρόφως, από την ισότητα προκύπτει ότι σε κάθε πραγματικό αριθμό x αντιστοιχεί μοναδικό σημείο M του άξονα με τετμημένη x. Το σημείο αυτό συμβολίζεται με

Καρτεσιανό Επίπεδο

Πάνω σε ένα επίπεδο σχεδιάζουμε δύο κάθετους άξονες 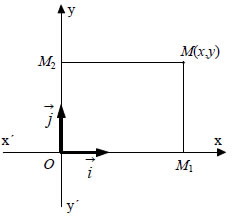και y΄y με κοινή αρχή Ο και μοναδιαία διανύσματα τα .
Λέμε τότε ότι έχουμε ένα ορθοκανονικό σύστημα συντεταγμένων στο επίπεδο ή

απλούστερα ένα σύστημα συντεταγμένων στο επίπεδο ή ακόμα ένα καρτεσιανό επίπεδο και το συμβολίζουμε με Oxy. Το σύστημα Oxy λέγεται ορθοκανονικό, γιατί είναι ορθογώνιο και κανονικό. Ορθογώνιο είναι, γιατί οι άξονες και y΄y είναι κάθετοι, και κανονικό, γιατί τα διανύσματα είναι ισομήκη.

Πάνω στο καρτεσιανό επίπεδο Oxy παίρνουμε ένα σημείο Μ. Από το Μ φέρνουμε την παράλληλη στον y΄y, που τέμνει τον στο και την παράλληλη στον , που τέμνει τον y΄y στο Αν x είναι η τετμημένη του ως προς τον άξονα και y η τετμημένη του ως προς τον άξονα y΄y, τότε ο x λέγεται τετμημένη του Μ και ο y τεταγμένη του Μ. Η τετμημένη και η τεταγμένη λέγονται συντεταγμένες του Μ.Έτσι σε κάθε σημείο Μ του επιπέδου αντιστοιχεί ένα ζεύγος συντεταγμένων.
Αλλά και αντιστρόφως σε κάθε ζεύγος (x,y) πραγματικών αριθμών αντιστοιχεί μοναδικό σημείο του επιπέδου, το οποίο βρίσκεται ως εξής: Πάνω στον άξονα παίρνουμε το σημείο και στον y΄y το σημείο Από τα και φέρνουμε παράλληλες στους άξονες y΄y και αντιστοίχως, που τέμνονται στο Μ. Το σημείο Μ είναι το ζητούμενο. Ένα σημείο Μ με τετμημένη x και τεταγμένη y συμβολίζεται και με ή απλά με

Συντεταγμένες Διανύσματος

Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και 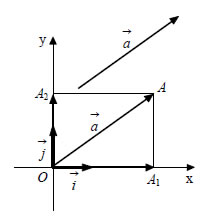ένα διάνυσμα του επιπέδου. Με αρχή το Ο σχεδιάζουμε το διάνυσμα Αν και είναι οι προβολές του Α στους άξονες και y΄y αντιστοίχως, έχουμε:

Αν x,y είναι οι συντεταγμένες του A, τότε ισχύει και Επομένως η ισότητα (1) γράφεται

Αποδείξαμε δηλαδή ότι το είναι γραμμικός συνδυασμός των
Στην παραπάνω κατασκευή οι αριθμοί x και y είναι μοναδικοί. Θα αποδείξουμε τώρα ότι και η έκφραση του ως γραμμικού συνδυασμού των και είναι μοναδική. Πράγματι, έστω ότι ισχύει και

Τότε θα έχουμε

Αν υποθέσουμε ότι δηλαδή ότι τότε θα ισχύει

Η σχέση αυτή, όμως, δηλώνει ότι που είναι άτοπο, αφού τα και δεν είναι συγγραμμικά. Επομένως που συνεπάγεται ότι και
Ώστε:
"Κάθε διάνυσμα του επιπέδου γράφεται κατά μοναδικό τρόπο στη μορφή ".
Τα διανύσματα λέγονται συνιστώσες του διανύσματος κατά τη διεύθυνση των , ενώ οι αριθμοί x, y λέγονται συντεταγμένες του στο σύστημα Oxy. Πιο συγκεκριμένα, ο x λέγεται

τετμημένη του και ο y λέγεται τεταγμένη του . Από τον τρόπο που ορίστηκαν οι συντεταγμένες ενός διανύσματος προκύπτει ότι:
"Δύο διανύσματα είναι ίσα αν και μόνο αν οι αντίστοιχες συντεταγμένες τους είναι ίσες".
Καθένα από τα ίσα διανύσματα με τετμημένη x και τεταγμένη y, θα το συμβολίζουμε με το διατεταγμένο ζεύγος

Συντεταγμένες Γραμμικού Συνδυασμού Διανυσμάτων

Αν γνωρίζουμε τις συντεταγμένες δύο διανυσμάτων και του καρτεσιανού επιπέδου, τότε μπορούμε να βρούμε τις συντεταγμένες του αθροίσματος του γινομένου και γενικά κάθε γραμμικού συνδυασμού των και . Πράγματι, αν τότε έχουμε:


Επομένως



ή ισοδύναμα


Γενικότερα, για το γραμμικό συνδυασμό έχουμε:



Για παράδειγμα, αν και τότε

Συντεταγμένες Μέσου Τμήματος

Ας θεωρήσουμε δύο σημεία 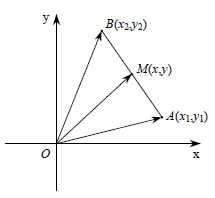και του καρτεσιανού επιπέδου και ας υποθέσουμε ότι είναι οι συντεταγμένες του μέσου Μ του ΑΒ.

Επειδή



Επομένως ισχύει

Συντεταγμένες Διανύσματος με Γνωστά Άκρα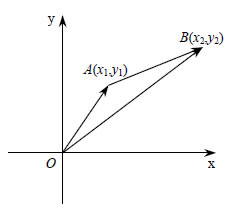

Ας θεωρήσουμε δύο σημεία και του καρτεσιανού επιπέδου και ας υποθέσουμε ότι (x,y) είναι οι συντεταγμένες του διανύσματος
Επειδή, και έχουμε:



Επομένως:

Οι συντεταγμένες (x,y) του διανύσματος με άκρα τα σημεία και δίνονται από τις σχέσεις

Δηλαδή

          τετμημένη του = τετμημένη του Β — τετμημένη του Α

          τεταγμένη του =τεταγμένη του Β — τεταγμένη του Α.

Για παράδειγμα, το διάνυσμα με αρχή το και πέρας το έχει συντεταγμένες και δηλαδή είναι ίσο με το

Μέτρο Διανύσματος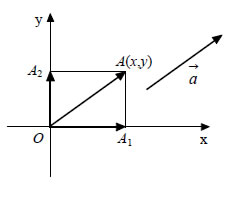

• Έστω ένα διάνυσμα του καρτεσιανού επιπέδου και Α το σημείο με διανυσματική ακτίνα Αν είναι οι προβολές του Α στους άξονες και y΄y αντιστοίχως, επειδή το σημείο Α έχει τετμημένη x και τεταγμένη y, θα ισχύει Έτσι θα έχουμε:

Επομένως:

Για παράδειγμα, αν 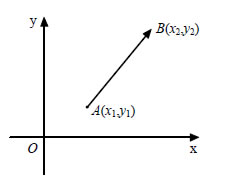τότε

• Ας θεωρήσουμε τώρα δύο σημεία και του καρτεσιανού επιπέδου. Επειδή η απόσταση (AB) των σημείων Α και Β είναι ίση με το μέτρο του διανύσματος σύμφωνα με τον τύπο (1) θα ισχύει:



Επομένως:

Η απόσταση των σημείων και είναι ίση με

Για παράδειγμα, η απόσταση των σημείων και είναι ίση με

ΕΦΑΡΜΟΓΕΣ

1. Αν A(-2,1) και B(1,4) είναι οι δύο κορυφές του παραλληλόγραμμου ABΓΔ και Κ(2,-3) το κέντρο του, να βρεθούν οι συντεταγμένες των κορυφών Γ και Δ.

ΛΥΣΗ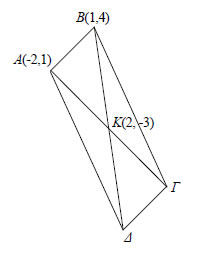

Αν 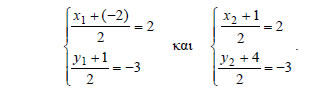και είναι οι δύο άλλες κορυφές του παραλληλόγραμμου, επειδή το Κ είναι το μέσον των ΑΓ και ΒΔ, έχουμε:

Επομένως,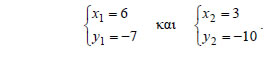

Άρα, οι συντεταγμένες των κορυφών Γ και Δ είναι (6,-7) και (3,-10) αντιστοίχως.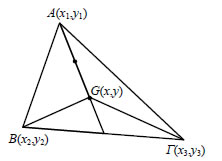

2. Να βρεθούν οι συντεταγμένες του κέντρου βάρους G του τριγώνου ABΓ, αν είναι γνωστές οι συντεταγμένες των κορυφών του.

ΛΥΣΗ

Αν είναι οι συντεταγμένες των κορυφών A, B, Γ αντιστοίχως και

είναι οι συντεταγμένες του κέντρου βάρους του ABΓ , επειδή (Εφαρμ. 1 § 1.3), θα έχουμε:

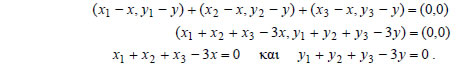Άρα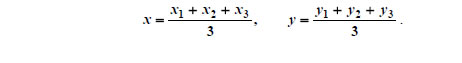

Συνθήκη Παραλληλίας Διανυσμάτων

Έστω δύο διανύσματα του καρτεσιανού επιπέδου.
— Αν τα διανύσματα είναι παράλληλα και υποθέσουμε ότι τότε θα υπάρχει τέτοιος, ώστε Επομένως, θα έχουμε ή ισοδύναμα:



οπότε θα ισχύει ή ισοδύναμα

— Αν τότε θα ισχύει

Δείξαμε δηλαδή ότι αν τα διανύσματα είναι παράλληλα, τότε



• Αντιστρόφως, αν τότε τα διανύσματα θα είναι παράλληλα. Πράγματι, επειδή έχουμε

Επομένως,

— Αν τότε οπότε, αν θέσουμε θα έχουμε



Άρα, και συνεπώς

— Αν x₂= 0 , τότε x₁ y₂= 0 , οπότε αν x₁= 0, τα διανύσματα θα είναι παράλληλα προς τον άξονα των τεταγμένων, άρα και μεταξύ τους παράλληλα, ενώ, αν y₂= 0 , τότε το θα είναι το μηδενικό διάνυσμα και άρα, παράλληλο προς το .

Αποδείξαμε λοιπόν ότι

Την ορίζουσα 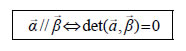που έχει ως 1η τη γραμμή τις συντεταγμένες του διανύσματος και ως 2η γραμμή τις συντεταγμένες του διανύσματος , τη λέμε ορίζουσα των διανυσμάτων και (με τη σειρά που δίνονται) και θα τη συμβολίζουμε με . Έτσι, η παραπάνω ισοδυναμία διατυπώνεται ως εξής:

Για παράδειγμα:

— Τα διανύσματα είναι παράλληλα, αφού ενώ

— Τα διανύσματα δεν είναι παράλληλα, αφού

Συντελεστής Διεύθυνσης Διανύσματος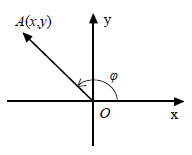

• Έστω ένα μη μηδενικό διάνυσμα και A το σημείο του επιπέδου για το οποίο ισχύει .Τη γωνία φ , που διαγράφει ο ημιάξονας αν στραφεί γύρω από το Ο κατά τη θετική φορά μέχρι να συμπέσει με την ημιευθεία ΟΑ, την ονομάζουμε γωνία που σχηματίζει το διάνυσμα με τον άξονα x'x. Είναι φανερό ότι

Για τη γωνία φ , όπως είναι γνωστό από την Τριγωνομετρία, αν το δεν είναι παράλληλο προς τον άξονα y'y , ισχύει

Το πηλίκο y/x της τεταγμένης προς την τετμημένη του διανύσματος 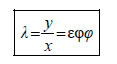με , το λέμε συντελεστή διεύθυνσης του και τον συμβολίζουμε με ή απλώς με λ. Επομένως:

Είναι φανερό ότι

— Αν y=0 , δηλαδή αν τότε ο συντελεστής διεύθυνσης του διανύσματος είναι ο λ=0.

— Αν x=0 , δηλαδή αν , τότε δεν ορίζεται συντελεστής διεύθυνσης του διανύσματος .

• Ας θεωρήσουμε τώρα δύο διανύσματα 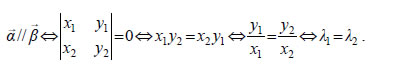με συντελεστές διεύθυνσης λ₁ και λ₂ αντιστοίχως. Τότε έχουμε τις ισοδυναμίες:

Επομένως, η συνθήκη παραλληλίας για δύο διανύσματα και 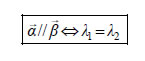με συντελεστές διεύθυνσης λ₁ και λ₂ διατυπώνεται ως εξής:

ΕΦΑΡΜΟΓΗ

Να βρεθούν οι τιμές του για τις οποίες τα σημεία είναι συνευθειακά.

ΛΥΣΗ

Τα σημεία Α,Β,Γ είναι συνευθειακά, αν και μόνο αν τα διανύσματα και είναι παράλληλα, δηλαδή, αν και μόνο αν .

Έχουμε λοιπόν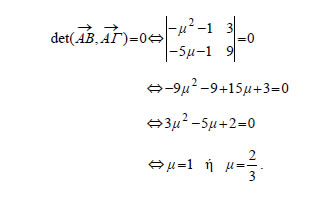

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Ποια είναι η θέση στο καρτεσιανό επίπεδο των σημείων M(x,y) για τα οποία ισχύει:
2.	Να βρείτε τις αποστάσεις των παρακάτω σημείων από τους άξονες x'x και yy' :
3.	Δίνεται το διάνυσμα . Για ποια τιμή του λ είναι:
4.	Δίνονται τα διανύσματα Να βρείτε το ώστε να είναι .
5.	Να βρείτε τον πραγματικό αριθμό x, ώστε τα διανύσματα να είναι ομόρροπα.
6.	Αν , ποιο διάνυσμα είναι συγγραμμικό με το και έχει διπλάσιο μέτρο από το ;