1.3 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ

Ορισμός Πολλαπλασιασμού Αριθμού με Διάνυσμα

Έστω λ ένας πραγματικός αριθμός με και ένα μη μηδενικό διάνυσμα. Ονομάζουμε γινόμενο του λ με το και το συμβολίζουμε με ή ένα διάνυσμα το οποίο:

• είναι ομόρροπο του , αν λ>0 και αντίρροπο του , αν λ<0 και

• έχει μέτρο

Αν είναι , τότε ορίζουμε ως το μηδενικό διάνυσμα

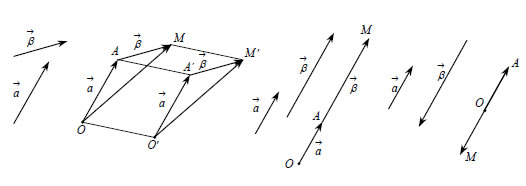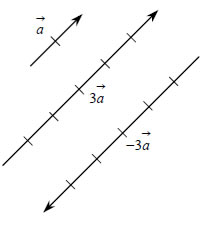Για παράδειγμα, αν το διάνυσμα τουδιπλανού σχήματος έχει μέτρο 2, τότε τοδιάνυσμα 3 είναι ομόρροπο με το καιέχει μέτρο , ενώ τοδιάνυσμα -3 είναι αντίρροπο με το , αλλά έχει και αυτό μέτρο ίσο με

Το γινόμενο το συμβολίζουμε και με

Ιδιότητες Πολλαπλασιασμού Αριθμού με Διάνυσμα

Για το γινόμενο πραγματικού αριθμού με διάνυσμα ισχύουν οι επόμενεςιδιότητες:

(1)    

(2)    

(3)    

ΑΠΟΔΕΙ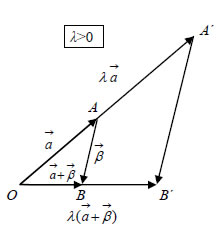ΞΗ*

(1) Υποθέτουμε ότι τα διανύσματα 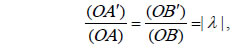είναι μη μηδενικά και ότι . Παίρνουμεένα σημείο Ο και σχεδιάζουμε τα διανύσματα . Τότε είναι . Σχεδιάζουμε επιπλέον τα διανύσματα και . Επειδή

τα τρίγωνα ΟΑΒ και ΟΑ΄Β΄ είναι όμοια και επομένως η πλευρά Α΄Β΄ είναιπαράλληλη με την ΑΒ και ισχύει

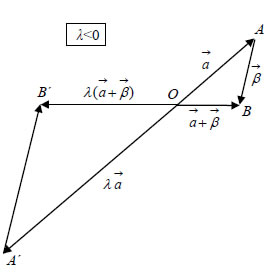Αυτό σημαίνει ότι.

Επομένως, επειδή έχουμε

Η ιδιότητα ισχύει προφανώς και ότανένα τουλάχιστον από τα διανύσματα είναι το μηδενικό ή όταν ο αριθμός λ είναι μηδέν.


Η απόδειξη των ιδιοτήτων (2) και (3) αφήνεται ως άσκηση.




Ως συνέπεια του ορισμού του γινομένου αριθμού με διάνυσμα και των παραπάνω ιδιοτήτων έχουμε:

Γραμμικός Συνδυασμός Διανυσμάτων

Ας θεωρήσουμε δύο διανύσματα . Από τα διανύσματα αυτά"παράγονται", για παράδειγμα, τα διανύσματα κτλ. Καθένα από τα διανύσματα αυτά λέγεται γραμμικός συνδυασμός των . Γενικά, ονομάζεται γραμμικός συνδυασμός δύο διανυσμάτων κάθε διάνυσμα της μορφής , όπου

Ανάλογα ορίζεται και ο γραμμικός συνδυασμός τριών ή περισσότερωνδιανυσμάτων. Έτσι, για παράδειγμα, το διάνυσμα είναι έναςγραμμικός συνδυασμός των

Συνθήκη Παραλληλίας Διανυσμάτων

Όπως είδαμε, αν δύο διανύσματα , όπου συνδέονται με τησχέση τότε τα διανύσματα αυτά είναι παράλληλα. Ισχύει όμως και τοαντίστροφο. Δηλαδή, αν τα διανύσματα είναι παράλληλα και τότε υπάρχει μοναδικός αριθμός λ τέτοιος ώστε . Πράγματι, ανθέσουμε τότε. Συνεπώς:

• Αν τότε

• Αν τότε

• Αν τότε

Σε κάθε λοιπόν περίπτωση υπάρχει λ και μάλιστα μοναδικός (ιδιότητα iv),τέτοιος, ώστε . Επομένως:

ΘΕΩΡΗΜΑ

Αν είναι δύο διανύσματα, με τότε

Για παράδειγμα, στο παρακάτω σχήμα αν Δ και Ε είναι τα μέσα των πλευρών ΑΒ και ΑΓ του τριγώνου ΑΒΓ, έχουμε: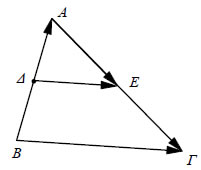

Αφού λοιπόν συμπεραίνουμε ότι και που σημαίνει ότι Ξαναβρίσκουμε δηλαδή τηγνωστή μας από την Ευκλείδεια Γεωμετρίασχέση

Διανυσματική Ακτίνα Μέσου Τμήματος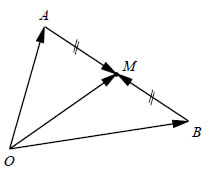

Ας πάρουμε ένα διάνυσμα 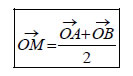και ένα σημείο αναφοράς Ο. Για τη διανυσματική ακτίνα του μέσου Μ του τμήματος ΑΒ έχουμε:



Επομένως,

. Άρα

ΕΦΑΡΜΟΓΕΣ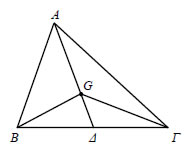

1. Να αποδειχτεί ότι ένα σημείο G είναι το βαρύκεντρο ενός τριγώνου ΑΒΓ, αν και μόνο αν ισχύει και ότι για οποιοδήποτε σημείο Ο ισχύει

ΑΠΟΔΕΙΞΗ

Γνωρίζουμε από την Ευκλείδεια Γεωμετρία ότι αν G είναι το κέντρο βάρους του τριγώνου ΑΒΓ, τότε , όπου ΑΔ η διάμεσος του τριγώνου. Επομένως, ισχύει , οπότε έχουμε

Αντιστρόφως, αν για ένα σημείο G ισχύει τότε θα έχουμε όπου Δ το μέσον της ΒΓ, οπότε θα ισχύει Έτσι, το σημείο G ανήκει στη διάμεσο ΑΔ και ισχύει ΑG = 2GΔ. Άρα, το G είναι το κέντρο βάρους του τριγώνου ΑΒΓ.
Από τη σχέση έχουμε: Άρα

2.Να αποδειχτεί ότι τα ευθύγραμμα τμήματα που ορίζουν τα μέσα των απέναντι πλευρών ενός τετραπλεύρου και τα μέσα των διαγωνίων του διέρχονται από το ίδιο σημείο και διχοτομούνται από το σημείο αυτό.

ΑΠΟΔΕΙΞΗ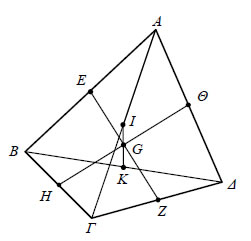

Έστω τα διανύσματα θέσεως των κορυφών Α, Β, Γ, Δ, αντιστοίχως, ενός τετράπλευρου ABΓΔ ως προς ένα σημείο αναφοράς Ο.
Τα διανύσματα θέσεως των μέσων Η της ΒΓ και Θ της ΑΔ είναι και αντιστοίχως και το διάνυσμα θέσεως του μέσου G του ΗΘ είναι το

Ομοίως βρίσκουμε ότι το διάνυσμα θέσεως των μέσων των τμημάτων ΕΖ και ΙΚ είναι το Άρα τα τμήματα ΗΘ, ΕΖ και ΙΚ
διέρχονται από το ίδιο σημείο και διχοτομούνται από αυτό.

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Αν είναι ένα διάνυσμα, τι μπορείτε να πείτε για το μέτρο και την κατεύθυνση του διανύσματος
2.	Να βρείτε το διάνυσμα σε καθεμιά από τις περιπτώσεις:
3.	Αν στο διπλανό σχήμα είναι , να αποδείξετε ότι