| 9. | Να εργαστείτε όπως στα σχήματα 1(β) και 3. | | 10. | Να εργαστείτε όπως στο σχήμα 1(γ). | | 11. | Να εργαστείτε όπως στο σχήμα 5. | | 12. | γ) 11 άτομα
δ) επίδοση ≥ 7. | | 13. | 20% | | 14. | ΝΑΙ. Το εμβαδόν πρέπει να είναι 100. | § 2.2 Β' Ομάδας | 1. | Για τη Λέσβο υπάρχει πτωτική τάση ενώ για τη Σαλαμίνα υπάρχει ανοδική τάση. Για τη Θάσο υπάρχει περίπου σταθερή κατάσταση. | | 2. | Να συμπληρώσετε τον πίνακα:
| Έτος | Ηλικία
≤ 20 21-30 ≥ 31 | Σύνολο | | | | | | 3. | Ανάλογα με την άσκηση 2. | | 4. | β) 355 γυναίκες, 434 άνδρες
γ) 692
δ) Δεν μπορούμε να ξέρουμε με τα στοιχεία που μας δίνονται. | | 5. | Να εργαστείτε όπως στο σχήμα 5. | | 6. | α) Φάρμακο Α 17,3% και Φάρμακο Β 26%. | | 7. | Επειδή v = 55 να χρησιμοποιήσετε κ = 7 κλάσεις με πλάτος c = 1,8. | § 2.3 Α' Ομάδας | 1. | 10, 12, 14, 16, 18, 20 με διάμεσο δ = 15 . | | 2. | α) ΝΑΙ, β) ΟΧΙ, γ) ΝΑΙ. | | 3. | 8,25%. | | 4. | α) 206,1cm β) 235 cm. | | 5. | 14,8. | | 6. | Και στις 3 περιπτώσεις έχουμε:
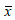 = 12gr, δ = 12gr, M0 = 13gr. = 12gr, δ = 12gr, M0 = 13gr. | | 7. | α) 14, β) 13. | | 8. | 291.000 δρχ. | | 9. | Οι 2 και 6. | | 10. | α) 2, β) 2, γ) 3. | | 11. | α) 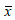 = 15,45 , β) δ = 15, γ) M0 = 15, = 15,45 , β) δ = 15, γ) M0 = 15,
δ) Q1 = 14, Q3 = 17. | | | 12. | α) 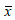 = 4,3, β) M0 = 3,3, = 4,3, β) M0 = 3,3,
γ) Q1 ≈ 2,33, δ ≈ 4, Q3 ≈ 6. | | 13. | α) 169,66cm, β) 170cm, γ) 169,67cm. | | 14. | α) Μικρότερη διασπορά έχουμε στη δεύτερη λίστα και μεγαλύτερη διασπορά στην τρίτη.
β) ΟΧΙ. | | 15. | α) 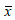 = 10, M0 = 11, δ = 11 = 10, M0 = 11, δ = 11
β) Q1 = 7, Q3 = 13
γ) R = 12, s = 3,87, cv = 38,7%. | | 16. | 2,47. | | 17. | α) 16%, β) 2,5%, γ) 50%, δ) 81,5%. | | 18. | α) 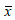 = 3, δ = 2 = 3, δ = 2
β) 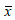 = 6, δ = 4 = 6, δ = 4
γ) 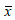 = 13, δ = 12 = 13, δ = 12
δ) 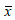 = 16, δ = 14. = 16, δ = 14. | | 19. | α) s2 = 4, β) s2 = 36, γ) s2 = 4, s2 = 4. | | 20. | v = 28. | § 2.3 Β' Ομάδας | 1. | β) 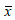 = 15, δ ≈ 15 = 15, δ ≈ 15
γ) P95 ≈ 19 | | 2. | 10 ή -2 | | 3. | α) 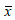 = 4400 δρχ., δ = 3500 δρχ., = 4400 δρχ., δ = 3500 δρχ.,
M0 = 3000 δρχ.
β) Αυξάνουν κατά 18%.
γ) Αυξάνουν κατά 100 δρχ. | | 4. | Να γίνουν οι πράξεις. | | 5. | α) 60, β) 33, γ) 5,2 εκατομ. δρχ.,
δ) 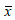 = 5,7 εκατομ. δρχ., s2 = 12,24 = 5,7 εκατομ. δρχ., s2 = 12,24
ε) Q1 ≈ 2,8 , δ ≈ 5,4 , Q3 ≈ 8,3 . | | 6. | α) s = 23,29, cv = 53,75%
β) Q = Q3 - Q1 ≈ 59 - 24 = 35 | | 7. | Να εργαστείτε όπως στο σχήμα 7. | § 2.4 Α' Ομάδας | 1. | Να εργαστείτε όπως στο σχήμα 16. | | 2. | i) 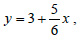 ii) y = 46,7 + 0,67x ii) y = 46,7 + 0,67x | | 3. | α) 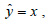 β) β) 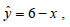
γ) 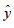 = 3,9 - 0,3x δ) = 3,9 - 0,3x δ) 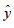 = 2,1 + 0,3x. = 2,1 + 0,3x. | | 4. | 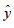 = 18,98 - 21,6x = 18,98 - 21,6x | | 5. | α) y = -0,35 + 1,07x, β) 16. | |