1ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ Εισαγωγή Στο χώρο της επιστήμης το 17ο αιώνα κυριαρχούσε η μελέτη της κίνησης των ουράνιων σωμάτων, καθώς και η μελέτη της κίνησης ενός σώματος πάνω ή κοντά στη Γη. Στη μελέτη αυτή προφανώς σημαντικό ρόλο έπαιζε ο προσδιορισμός του μέτρου της ταχύτητας και της διεύθυνσης της κίνησης του σώματος σε μια δεδομένη χρονική στιγμή. Όπως θα δούμε στη συνέχεια, αν η θέση του σώματος μια χρονική στιγμή t εκφράζεται με τη συνάρτηση x=f(t), τότε ο προσδιορισμός του μέτρου και της διεύθυνσης της ταχύτητάς του τη χρονική στιγμή t ανάγεται στον προσδιορισμό του ρυθμού μεταβολής της x=f(t) ως προς t ή, όπως ονομάστηκε αργότερα, της παραγώγου της x=f(t). Έτσι, προβλήματα σχετικά με την κίνηση ενός σώματος, καθώς και άλλα που θα συναντήσουμε αργότερα, οδήγησαν στη γένεση του Διαφορικού Λογισμού. Θεμελιωτές του είναι οι Newton (1642-1727) και Leibniz (16461716), οι οποίοι εισήγαγαν τη γενική έννοια της “παραγώγου” και του “διαφορικού”, βελτίωσαν τις μεθόδους του Διαφορικού Λογισμού και τις χρησιμοποίησαν στην επίλυση προβλημάτων της Γεωμετρίας και της Μηχανικής. Η ανάπτυξη του Διαφορικού Λογισμού δε σταμάτησε το 17ο αιώνα, αλλά συνεχίστηκε το 18ο αιώνα με τη σημαντική συμβολή των αδελφών Jacob Bernoulli (1654-1705) και Johann Bernoulli (1667-1748), του Euler (1707-1783), κορυφαίου μαθηματικού της εποχής, του Lagrange (1736-1813) και πολλών άλλων. Τέλος, η αυστηρή θεμελίωση του Διαφορικού Λογισμού έγινε από τους μαθηματικούς του 19ου αιώνα όπως του Bolzano (1781-1848), του Cauchy (1789-1857) και του Weierstrass (1815-1897). 1.1 ΣΥΝΑΡΤΗΣΕΙΣ Ορισμός συνάρτησης Είδαμε σε προηγούμενες τάξεις ότι συνάρτηση (function) είναι μια διαδικασία με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. |
|
Στο κεφάλαιο αυτό θα ασχοληθούμε με συναρτήσεις στις οποίες το σύνολο Α, που λέγεται πεδίο ορισμού της συνάρτησης, είναι υποσύνολο του συνόλου R των πραγματικών αριθμών, ενώ το Β συμπίπτει με το R. Οι συναρτήσεις αυτές λέγονται πραγματικές συναρτήσεις πραγματικής μεταβλητής και τις οποίες στο εξής θα τις λέμε απλώς συναρτήσεις. Η συνάρτηση συμβολίζεται συνήθως με ένα από τα μικρά γράμματα f, g, h, φ, σ κτλ. του λατινικού ή του ελληνικού αλφαβήτου. y=f(x) και διαβάζουμε “y ίσον f του x”. Το f (x) λέγεται τιμή της f στο x. Το γράμμα x, που συμβολίζει οποιοδήποτε στοιχείο του Α, ονομάζεται ανεξάρτητη μεταβλητή, ενώ το y, που παριστάνει την τιμή της συνάρτησης στο x και εξαρτάται από την τιμή του x, λέγεται εξαρτημένη μεταβλητή. Σε μια συνάρτηση συνήθως η τιμή της εκφράζεται με έναν αλγεβρικό τύπο, για παράδειγμα Όταν το f(x) εκφράζεται μόνο με έναν αλγεβρικό τύπο, τότε το πεδίο ορισμού της συνάρτησης είναι το "ευρύτερο" υποσύνολο του R στο οποίο το f(x) έχει νόημα πραγματικού αριθμού. Έτσι, η παραπάνω συνάρτηση ΣΧΟΛΙΟ Αν και συνήθως χρησιμοποιούμε το γράμμα f για το συμβολισμό μιας συνάρτησης και τα γράμματα x και y για το συμβολισμό της ανεξάρτητης και της εξαρτημένης μεταβλητής αντιστοίχως, ωστόσο μπορούμε να χρησιμοποιήσουμε και άλλα γράμματα. |
Έτσι, για παράδειγμα, οι τύποι 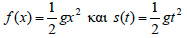 ορίζουν την ίδια συνάρτηση. ορίζουν την ίδια συνάρτηση. Πράξεις με Συναρτήσεις Αν δύο συναρτήσεις f, g ορίζονται και οι δύο σε ένα σύνολο Α, τότε ορίζονται και οι συναρτήσεις:
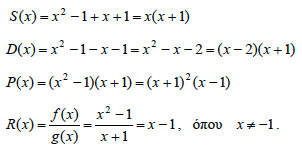 Γραφική Παράσταση Συνάρτησης Έστω μια συνάρτηση f με πεδίο ορισμού ένα σύνολο Α. Όπως είδαμε σε προηγούμενες τάξεις γραφική παράσταση ή καμπύλη της f σε ένα καρτεσιανό σύστημα συντεταγμένων Oxy λέγεται το σύνολο των σημείων M(x,(f(x)) για όλα τα |
|
Παρατηρούμε ότι στη γραφική παράσταση της Μονοτονία - Ακρότατα Συνάρτησης
|
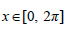 είναι είναι 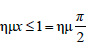 και και 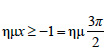 . Δηλαδή, όπως λέμε, η συνάρτηση f(x)=ημx έχει ολικό μέγιστο (maximum) για . Δηλαδή, όπως λέμε, η συνάρτηση f(x)=ημx έχει ολικό μέγιστο (maximum) για 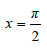 και ολικό ελάχιστο (minimum) για και ολικό ελάχιστο (minimum) για 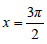 . .
Από τη γραφική παράσταση της συνάρτησης g του σχήματος 4 προκύπτει ότι για x=x1 η τιμή της g είναι μικρότερη από τις τιμές της g σε όλα τα x που ανήκουν σε ένα ανοικτό διάστημα το οποίο περιέχει το x1, ή, όπως λέμε σε μια περιοχή του x1. Στην περίπτωση αυτή λέμε ότι η συνάρτηση g έχει στο σημείο x1 τοπικό ελάχιστο. Το ίδιο συμβαίνει και για x=x3. Οι τιμές g(x1) και g(x3) λέγονται τοπικά ελάχιστα της συνάρτησης. Επίσης, για x=x4 η τιμή g(x4) είναι μεγαλύτερη από τις τιμές της g σε όλα τα x που ανήκουν σε μια περιοχή του x4. Λέμε ότι η συνάρτηση g έχει στο σημείο x4 τοπικό μέγιστο. Το ίδιο συμβαίνει και για x=x2. Οι τιμές g(x2) και g(x4) λέγονται τοπικά μέγιστα της συνάρτησης. Παρατηρούμε ότι ένα τοπικό ελάχιστο μπορεί να είναι μεγαλύτερο από ένα τοπικό μέγιστο. Για παράδειγμα, το τοπικό ελάχιστο g(x1) είναι μεγαλύτερο από το τοπικό μέγιστο g(x4). Μια συνάρτηση f με πεδίο ορισμού το Α, λέμε ότι παρουσιάζει: Τοπικό μέγιστο στο 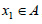 , όταν , όταν 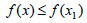 για κάθε x σε μια περιοχή του x1, και τοπικό ελάχιστο στο για κάθε x σε μια περιοχή του x1, και τοπικό ελάχιστο στο 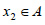 όταν όταν 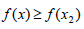 για κάθε x σε μια περιοχή του x2. για κάθε x σε μια περιοχή του x2.Τα μέγιστα και τα ελάχιστα μιας συνάρτησης, τοπικά ή ολικά, λέγονται ακρότατα της συνάρτησης. Όριο Συνάρτησης Έστω η συνάρτηση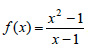 , η οποία δεν ορίζεται για x=1. Ας εξετάσουμε όμως τη συμπεριφορά της f για τιμές του x κοντά στο 1. , η οποία δεν ορίζεται για x=1. Ας εξετάσουμε όμως τη συμπεριφορά της f για τιμές του x κοντά στο 1. |
| Ο παρακάτω πίνακας δείχνει τις τιμές του f(x) για τιμές του x κοντά στο 1.
Από τον παραπάνω πίνακα βλέπουμε ότι όταν το x παίρνει τιμές πολύ κοντά στο 1 (και από τις δύο πλευρές του 1), το f(x) παίρνει τιμές πολύ κοντά στο 2. Στο ίδιο συμπέρασμα φτάνουμε, αν παρατηρήσουμε ότι για
οπότε όταν το x παίρνει τιμές που τείνουν στο 1 Με το προηγούμενο παράδειγμα παρουσιάσαμε με απλό τρόπο και χωρίς μαθηματική αυστηρότητα την έννοια του ορίου μιας συνάρτησης f σε ένα σημείο x0 που δεν ανήκει στο πεδίο ορισμού της, υπάρχουν όμως σημεία του πεδίου ορισμού της πολύ κοντά στο x0. Τίποτα βέβαια δεν αποκλείει την αναζήτηση του ορίου μιας συνάρτησης και σε ένα σημείο x0 που να ανήκει στο πεδίο ορισμού της. Για παράδειγμα, έστω η συνάρτηση
|
Αν οι συναρτήσεις f και g έχουν στο x0 όρια πραγματικούς αριθμούς, δηλαδή αν 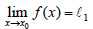 και και 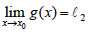 όπου όπου 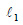 και και 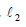 πραγματικοί αριθμοί, τότε αποδεικνύεται ότι: πραγματικοί αριθμοί, τότε αποδεικνύεται ότι:Έτσι, για παράδειγμα, για την πολυωνυμική συνάρτηση |
ΕΦΑΡΜΟΓΕΣ Να υπολογιστούν τα όρια: 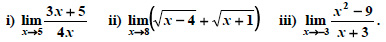 ΛΥΣΗ i)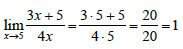 ii) 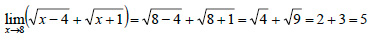 iii) 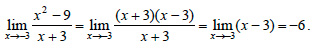 |
Ασκήσεις
| ||||||||||||||||||||
| ||||||||||||