4.7 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ

Το ζήτημα της διαιρετότητας των ακεραίων είναι κυρίαρχο θέμα στη Θεωρία των Αριθμών. Μια έννοια που βοηθάει στη μελέτη και επίλυση προβλημάτων διαιρετότητας είναι η έννοια των ισοϋπόλοιπων αριθμών. Για να γίνει αντιληπτή η έννοια αυτή, ας εξετάσουμε, για παράδειγμα, τα υπόλοιπα των διαιρέσεων των ακεραίων με τον αριθμό 5.

Από την ταυτότητα της αλγοριθμικής διαίρεσης γνωρίζουμε ότι το υπόλοιπο της διαίρεσης ενός ακεραίου με το 5 είναι ένας από τους πέντε ακεραίους 0,1,2,3 και 4. Έτσι έχουμε

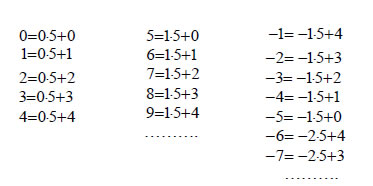Παρατηρούμε ότι οι αριθμοί 2,7, -3 διαιρούμενοι με 5 αφήνουν το ίδιο υπόλοιπο 2. Λέμε ότι οι αριθμοί αυτοί είναι ισοϋπόλοιποι με μέτρο 5. Ομοίως, λέμε ότι και οι αριθμοί 4,9, -1, -6 είναι ισοϋπόλοιποι με μέτρο 5, αφού διαιρούμενοι με 5 αφήνουν το ίδιο υπόλοιπο 4. Γενικότερα, έχουμε:

ΟΡΙΣΜΟΣ

Έστω m ένας θετικός ακέραιος. Δύο ακέραιοι α και β λέγονται ισοϋπόλοιποι με μέτρο m , όταν διαιρούμενοι με m αφήνουν το ίδιο υπόλοιπο.

Για να δηλώσουμε ότι οι α και β είναι ισοϋπόλοιποι με μέτρο m, γράφουμε

και διαβάζουμε "α ισοϋπόλοιπος του β μόντουλο m ". Αν ο ακέραιος α δεν είναι ισοϋπόλοιπος του β μόντουλο m , γράφουμε . Έτσι, .

Αν το υπόλοιπο της ευκλείδειας διαίρεσης του α με τον m είναι υ , τότε προφανώς ισχύει

Από την ισότητα της ευκλείδειας διαίρεσης προκύπτει το επόμενο θεώρημα, με το οποίο μπορούμε να διαπιστώσουμε αν δυο αριθμοί είναι ισοϋπόλοιποι.

ΘΕΩΡΗΜΑ 11

, αν και μόνον αν .

ΑΠΟΔΕΙΞΗ

Αν , τότε από τις ευκλείδειες διαιρέσεις των α και β με το m έχουμε α=κm + υ, β= λm +υ . Επομένως, α - β=(κ - λ)m , που σημαίνει ότι .

Αντιστρόφως, αν , τότε α - β=ρm, δηλαδή α= β + ρm για κάποιο ακέραιο ρ . Αν ο β διαιρούμενος με τον m δίνει πηλίκο κ και υπόλοιπο υ , τότε . Επομένως, α= κm +υ +ρm = (κ +ρ)m +υ , που σημαίνει ότι ο α διαιρούμενος με m δίνει υπόλοιπο επίσης υ. ■

Το συμβολισμό τον εισήγαγε ο Gauss(1777-1855). Όπως εξήγησε ο ίδιος, υιοθέτησε το σύμβολο , επειδή η σχέση έχει ανάλογες ιδιότητες με την ισότητα.

Πράγματι, ως άμεσες συνέπειες του ορισμού των ισοϋπόλοιπων αριθμών προκύπτουν οι ιδιότητες: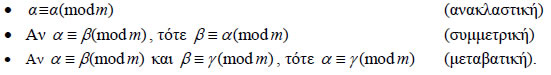

Επίσης, ισχύει το επόμενο θεώρημα:

ΘΕΩΡΗΜΑ 12

Αν

τότε

Εικόνα

ΑΠΟΔΕΙΞΗ

Έχουμε α - β=κm και γ - δ=λm , όπου κ,λ ακέραιοι. Επομένως:

(α +γ) - (β +δ)= (α -β) + (γ-δ)= κm +λm=(κ + λ)m , που σημαίνει ότι

(α - γ) - (β - δ)= (α -β) - (γ-δ)= κm - λm=(κ - λ)m, που σημαίνει ότι

(αγ - βδ)= αγ - βγ + βγ - βδ = (α - β)γ - (γ - δ)β =κmγ - λmβ=(κγ - λβ)m, που σημαίνει ότι

Η σχέση λέγεται ισοτιμία.

Ως άμεση συνέπεια του θεωρήματος προκύπτει ότι:

Αν για κάθε ακέραιο γ .

Το παραπάνω θεώρημα γενικεύεται και για περισσότερες από δύο ισοτιμίες.

Δηλαδή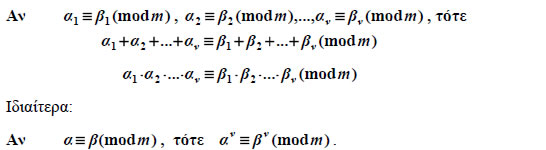

Ενώ, με πολλαπλασιασμό των μελών μιας ισοτιμίας με τον ίδιο ακέραιο προκύπτει πάλι ισοτιμία, δεν ισχύει το ίδιο και για τη διαίρεση. Για παράδειγμα, αν διαιρέσουμε τα μέλη της ισοτιμίας με 2, δεν προκύπτει ισοτιμία. Πράγματι, .

Οι ισοτιμίες εμφανίζονται συχνά στην καθημερινή μας ζωή. Για παράδειγμα, ο ωροδείκτης των ρολογιών δείχνει την ώρα modulo 12 και ο χιλιομετρικός δείκτης των αυτοκινήτων δείχνει τα χιλιόμετρα που έχουμε διανύσει modulo 100.000. Έτσι, όταν η ώρα είναι 18, το ρολόι δείχνει 6, που είναι το υπόλοιπο της διαίρεσης του 18 με το 12, και όταν ένα αυτοκίνητο έχει διανύσει συνολικά 245.000 km, δείχνει 45.000 km, που είναι το υπόλοιπο της διαίρεσης του 245.000 με το 100.000.

ΕΦΑΡΜΟΓΕΣ

1. Έστω η δεκαδικ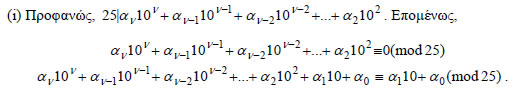ή παράστα-ση ενός θετικού ακέραιου N και το άθροισμα των ψηφίων του. Να αποδειχτούν τα κριτήρια διαιρετότητας:

(i) , αν και μόνο αν .

(ii) , αν και μόνο αν .

ΑΠΟΔΕΙΞΗ

Δηλαδή, ένας ακέραιος διαιρείται με 25, αν και μόνο αν το τελευταίο διψήφιο τμήμα του διαιρείται με 25.

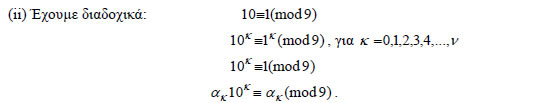Επομένως,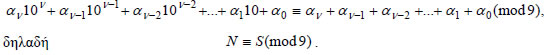. Προσθέτουμε τις ισοτιμίες κατά μέλη και έχουμε:

2. Να βρεθεί το τελευταίο ψηφίο του αριθμού 3¹⁹⁹⁹ + 2¹⁹⁹⁹

ΛΥΣΗ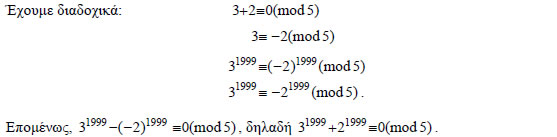

Άρα , που σημαίνει ότι ο αριθμός 3¹⁹⁹⁹ + 2¹⁹⁹⁹ λήγει σε 0 ή σε 5. Όμως, ο αριθμός 3¹⁹⁹⁹ + 2¹⁹⁹⁹ είναι περιττός ως άθροισμα ενός περιττού και ενός άρτιου και άρα λήγει σε 5.

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ
1.	Δίνονται τα σύνολα A={33, -17, 23, 35, 41, -20} και B={0, 1, 2, 3, 4, 5, 6} . Να αντιστοιχίσετε τα στοιχεία σε εκείνα τα στοιχεία για τα οποία ισχύει .
2.	Ποιες από τις παρακάτω προτάσεις είναι αληθείς;

3.	Να βρείτε τους διψήφιους θετικούς ακέραιους α για τους οποίους ισχύει .
4.	Να βρείτε τους διψήφιους θετικούς ακέραιους α για τους οποίους ισχύει
5.	Να βρείτε το υπόλοιπο της διαίρεσης
6.	Να αποδείξετε ότι για κάθε ισχύει
7.	Να βρείτε (i) το τελευταίο ψηφίο του αριθμού 3¹⁹⁹⁸ (ii) τα δύο τελευταία ψηφία του αριθμού 7²⁰⁰³ .

Β' ΟΜΑΔΑΣ
1.	Να αποδείξετε ότι ο ακέραιος 3α² -1 , όπου , δεν είναι ποτέ τετράγωνο ακεραίου.
2.	Να αποδείξετε ότι για κάθε θετικό πρώτο .
3.	Να βρείτε τις τιμές του για τις οποίες ισχύει .
4.	Να βρείτε τις τιμές του για τις οποίες ισχύει .
5.	Να αποδείξετε ότι για κάθε ισχύει
6.	Έστω . Να αποδείξετε ότι
7.	Αν , να αποδείξετε ότι (α,m)=(β,m) .
8.	Να αποδείξετε ότι:

9.	Να αποδείξετε ότι: (i) Για κάθε θετικό ακέραιο α ισχύει ή 1 ή 4(mod5). (ii) Οι αριθμοί είναι άρρητοι.
10.	Να αποδείξετε ότι για κάθε θετικό πρώτο και στη συνέχεια να αποδείξετε ότι οι αριθμοί είναι σύνθετοι για όλους τους θετικούς πρώτους που είναι μεγαλύτεροι από τον 3.
11.	Αν p,q είναι θετικοί πρώτοι με , να αποδείξετε ότι .
12.	Να βρείτε το ψηφίο των μονάδων των αριθμών 77⁷⁷ και 333³³³ .
13.	Να αποδείξετε ότι ο αριθμός 2¹⁹⁹⁹ +2¹⁹⁹⁷ -1 είναι σύνθετος.

ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ

1.	Να αποδείξετε ότι από v διαδοχικούς ακεραίους ακριβώς ένας διαιρείται με το v.
2.	Να βρείτε τους θετικούς ακεραίους α,β,γ για τους οποίους ισχύει
3.	Να αποδείξετε ότι το άθροισμα διαδοχικών περιττών φυσικών είναι σύνθετος αριθμός.
4.	Έστω α,β δύο θετικοί ακέραιοι, με (α,β)=1 . Να αποδείξετε ότι
5.	(i) Έστω α,β θετικοί ακέραιοι. Να αποδείξετε ότι • Αν (α,β)=1 , τότε (α +β, αβ)=1. • (α +β, [α,β])=(α,β) (ii) Να βρείτε τους θετικούς ακεραίους α,β για τους οποίους ισχύει α+β=114 και [α,β]=360 .
6.	Έστω p,q δύο θετικοί πρώτοι, διαφορετικοί μεταξύ τους. Να αποδείξετε ότι τα στοιχεία του συνόλου είναι διαφορετικά ανά δύο.

7.	(i) Να αποδείξετε ότι για κάθε θετικό ακέραιο . (ii) Να βρείτε τις θετικές ακέραιες λύσεις της εξίσωσης 2^x=x² .
8.	Δίνονται οι θετικοί ακέραιοι . Να αποδείξετε ότι (i) Αν ο α^v -1 είναι πρώτος, τότε α=2 και ο v είναι πρώτος. (ii) Αν ο α^v +1 είναι πρώτος, τότε v=2^κ και ο α είναι πρώτος.
9.	Να αποδείξετε ότι (i ) (ii) Η εξίσωση x²+y²=1998 δεν έχει ακέραιες λύσεις.
10.	(i) Να αποδείξετε ότι (ii) Να βρείτε τα δύο τελευταία ψηφία του 9²⁰⁰² .
11.	(i) Να βρείτε τους θετικούς ακέραιους για τους οποίους ισχύει: (ii) Να βρείτε τα ορθογώνια με ακέραια μήκη πλευρών, των οποίων το εμβαδόν και η περίμετρος είναι αριθμητικά ίσα. (iii) Έστω ένα σημείο Α ενός επιπέδου. Για ποιες τιμές του v ο χώρος γύρω από το Α μπορεί να καλυφθεί με κανονικά v-γωνα, τα οποία δεν έχουν κοινά εσωτερικά τους σημεία.
12.	Να βρείτε ο εμβαδόν του τετραγώνου που μπορεί να χωριστεί σε 25 μικρότερα τετράγωνα, από τα οποία τα 24 έχουν πλευρά ίση με 1, ενώ το ένα έχει πλευρά με μήκος ακέραιο αριθμό διαφορετικό από 1.
13.	Μπορείτε να γράψετε μερικούς αριθμούς, χρησιμοποιώντας καθένα από τα δέκα ψηφία 0, 1, 2,...., 8, 9 μόνο μία φορά, ώστε το άθροισμα των αριθμών αυτών να είναι ίσο με 100.
14.	Να βρείτε τους , σε καθεμιά από τις παρακάτω περιπτώσεις
15.	Αν , να αποδείξετε ότι (α²,β²)=(α,β)² .
16.	Έστω με (α,β)=1 . Αν το γινόμενο των α και β είναι τετράγωνο φυσικού αριθμού, να αποδείξετε ότι καθένας από τους α και β είναι τετράγωνο φυσικού αριθμού.

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

•	Σε καθεμιά από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Α, αν ο ισχυρισμός είναι αληθής και το γράμμα Ψ, αν ο ισχυρισμός είναι ψευδής, αιτιολογώντας συγχρόνως την απάντησή σας.
1.	Η παρακάτω ισότητα είναι η ταυτότητα της ευκλείδειας διαίρεσης του α με το β:
2.
3.
4.
5.
6.	Υπάρχουν , ώστε
7.
8.

• Να κυκλώσετε τη σωστή απάντηση σε καθεμιά από τις παρακάτω περιπτώσεις:

1	Αν είναι η ταυτότητα της διαίρεσης του α με τον 4 και β=(x+1)6 +3 είναι η ταυτότητα της διαίρεσης του β με τον (x+1) , τότε A:x=0, B:x=1, Γ:x=2, Δ:x=3.
2	Αν α=3κ +υ είναι η ταυτότητα της διαίρεσης του α με τον 3 και ο α είναι άρτιος, τότε A: κ περιττός και υ άρτιος B: κ άρτιος και υ περιττός Γ: κ,υ άρτιοι ή κ,υ περιττοί
3	Αν δ=(4ν+3, 4ν-1), τότε A:δ=4, B:δ=2, Γ:δ=1, Δ: Ο δ εξαρτάται από το ν
4	Αν ο αριθμός x 2722 x διαιρείται με τον 12, τότε A:x=1, B:x=4, Γ:x=7, Δ:x=2
5	Αν , τότε ο (α,β,γ) είναι A:, B:, Γ:2, Δ:3
6	Αν ο v είναι περιττός, τότε ο ακέραιος