4.6 Η ΓΡΑΜΜΙΚΗ ΔΙΟΦΑΝΤΙΚΗ ΕΞΙΣΩΣΗ

Εισαγωγή

Ένα από τα αρχαιότερα προβλήματα της Θεωρίας Αριθμών είναι η αναζήτηση των ακέραιων αριθμών που ικανοποιούν κάποιες δεδομένες σχέσεις. Με σύγχρονη ορολογία θα διατυπώσουμε το ίδιο πρόβλημα ως επίλυση, στο Ζ, πολυωνυμικών εξισώσεων με έναν ή περισσότερους αγνώστους και με ακέραιους συντελεστές. Ο κλάδος που ασχολείται με αυτό το ζήτημα ονομάζεται Διοφαντική Ανάλυση προς τιμήν του Διόφαντου (250 περίπου μ.Χ.), που ασχολήθηκε συστηματικά με τέτοιου είδους προβλήματα στο έργο του "Αριθμητικά".

Η αναζήτηση Πυθαγόρειων τριάδων (δηλαδή ακέραιων λύσεων της εξίσωσης x²+y²= z² ) συγκαταλέγεται ανάμεσα στα κλασικά προβλήματα της Διοφαντικής Ανάλυσης. Υπάρχουν ενδείξεις ότι η λύση αυτού του προβλήματος (που δίνεται σήμερα από τους τύπους x=μ² - v², y=2μν z=μ² + v² ) ήταν γνωστή στους Βαβυλώνιους, αλλά η πλήρης θεωρητική διαπραγμάτευση του ζητήματος έγινε από τους Αρχαίους Έλληνες μαθηματικούς. Ο Ευκλείδης διατυπώνει το πρόβλημα στη μορφή

"Ευρείν δύο τετραγώνους αριθμούς, ώστε και το συγκείμενον εξ αυτών είναι τετράγωνον"

και δίνει τη γενική λύση στη γεωμετρική γλώσσα των "Στοιχείων" (Βιβλίο Χ, Λήμμα 1, Πρότ. 28).

Ο Διόφαντος διαπραγματεύεται το ίδιο πρόβλημα στα "Αριθμητικά"

"Τον επιταχθέντα τετράγωνον διελείν εις δύο τετραγώνους",

αλλά η λύση που δίνει βρίσκεται πιο κοντά στο σύγχρονο αλγεβρικό τρόπο σκέψης. Αυτό ακριβώς το πρόβλημα ήταν η αφορμή να ισχυριστεί ο P. Fermat (1601-1665) ότι η διοφαντική εξίσωση x^v+y^v= z^v είναι αδύνατη, όταν ο ν είναι φυσικός μεγαλύτερος του 2, σημειώνοντας μάλιστα πάνω στο βιβλίο του Διόφαντου που μελετούσε: "έχω μια αληθινά θαυμάσια απόδειξη αυτής της πρότασης, αλλά το περιθώριο είναι πολύ στενό για να τη χωρέσει". Ο ισχυρισμός αυτός του Fermat αποδείχτηκε αληθής το 1994 από τον A. Wiles, αφού υπήρξε για 350 χρόνια ένα από τα διασημότερα άλυτα προβλήματα της Θεωρίας Αριθμών.

Η επίλυση διοφαντικών εξισώσεων βαθμού μεγαλύτερου του 2ου αποτελεί ένα ανοικτό μαθηματικό πρόβλημα, καθώς δεν έχουν βρεθεί γενικοί τύποι επίλυσης. Ο D. Hilbert διατύπωσε το 1900, ως ένα ζήτημα βασικής μαθηματικής έρευνας στη διάρκεια του 20ού αιώνα, την αναζήτηση ενός αλγόριθμου επίλυσης μιας διοφαντικής εξίσωσης με οποιοδήποτε αριθμό αγνώστων. Το 1970, ο Y. Matyasevich, σε ηλικία 22 χρόνων, απέδειξε ότι ένας τέτοιος αλγόριθμος δεν υπάρχει.

Επίλυση Γραμμικής Διοφαντικής Εξίσωσης

Έστω η εξίσωση αx +βy = γ , όπου α,β,γ ακέραιοι με . Αν αναζητούμε ακέραιες λύσεις της εξίσωσης αυτής, δηλαδή ζεύγη ακεραίων (x,y) που την επαληθεύουν, τότε λέμε ότι έχουμε να λύσουμε μια γραμμική διοφαντική εξίσωση.

Μερικές διοφαντικές εξισώσεις μπορεί να έχουν πολλές λύσεις, όπως, για παράδειγμα, η 3x +6y = 18 , για την οποία μπορούμε να διαπιστώσουμε με αντικατάσταση ότι τα ζεύγη (4,1), ( -6,6), (10, -2) είναι ακέραιες λύσεις της.Υπάρχουν όμως διοφαντικές εξισώσεις που δεν έχουν καμιά λύση. Για παράδειγμα, η διοφαντική εξίσωση 2x + 6y = 13 δεν έχει καμιά λύση, αφού για όλες τις ακέραιες τιμές των το πρώτο μέλος της είναι άρτιος αριθμός, ενώ το δεύτερο μέλος της είναι περιττός αριθμός. Το θεώρημα που ακολουθεί δίνει απάντηση στο ερώτημα πότε μια διοφαντική εξίσωση έχει λύση, και αν έχει, πόσες είναι αυτές οι λύσεις.

ΘΕΩΡΗΜΑ 10

ΑΠΟΔΕΙΞΗ

• Έστω ότι ,δηλαδή ότι . Γνωρίζουμε ότι για τον δ=(α,β) υπάρχουν ακέραιοι κ,λ τέτοιοι, ώστε

Πολλαπλασιάζοντας τα μέλη της (1) με μ βρίσκουμε μκα + μλβ= μδ , δηλαδή

Άρα, το ζεύγος (κμ,λμ) είναι μια λύση της εξίσωσης.

Αντιστρόφως, αν (x₀,y₀) είναι μια λύση της διοφαντικής εξίσωσης, τότε θα ισχύει αx₀+ βy₀ = γ . Επειδή , συμπεραίνουμε ότι , δηλαδή .

• Έστω (x₀,y₀) μια λύση της διοφαντικής εξίσωσης αx +βy = γ . Τότε θα ισχύει

Αν (x',y') είναι μια άλλη λύση της διοφαντικής εξίσωσης αx +βy = γ , τότε θα ισχύει

οπότε με αφαίρεση των δυο ισοτήτων κατά μέλη παίρνουμε ή ισοδύναμα

Επειδή δ=(α,β), οι αριθμοί είναι πρώτοι μεταξύ τους. Από την (2), με διαίρεση και των δύο μελών της με δ , έχουμε

Έτσι, ο p διαιρεί το πρώτο μέλος της ισότητας, οπότε θα διαιρεί και το δεύτερο και επειδή είναι πρώτος προς το σ , θα διαιρεί τον ακέραιο y₀ - y'. Επομένως, θα υπάρχει ακέραιος t , τέτοιος, ώστε y_o - y' =pt , δηλαδή , οπότε, λόγω της (2), θα είναι .

Αντιστρόφως, για κάθε 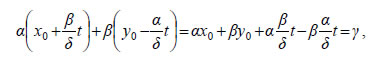, ισχύει

που σημαίνει ότι και το ζεύγος είναι λύση της εξίσωσης.

Ώστε, αν μια διοφαντική εξίσωση έχει μια λύση (x₀,y₀) , τότε έχει άπειρες λύσεις της μορφής ■

Στην περίπτωση που είναι (α,δ)=1 , οι παραπάνω τύποι παίρνουν τη μορφή:

Η γεωμετρική ερμηνεία του παραπάνω θεωρήματος προκύπτει, αν λάβουμε υπόψη ότι κάθε εξίσωση της μορφής αx +βy = γ, με , παριστάνει στο επίπεδο μια ευθεία. Στην περίπτωση που, η ευθεία αυτή διέρχεται από άπειρα σημεία με ακέραιες συντεταγμένες, αν και μόνο αν ο , όπου δ=(α,β) .

Για παράδειγμα, η ευθεία 2x +3y = 1 διέρχεται από άπειρο πλήθος σημείων με ακέραιες συντεταγμένες, ενώ η 6x +4y = 5 δε διέρχεται από κανένα τέτοιο σημείο.

ΕΦΑΡΜΟΓΗ

Κάποιος οδηγός που χρειάζεται κέρματα, για να ρίξει στο μηχάνημα στάθμευσης (parking), ζητάει από τον περιπτερά να του ανταλλάξει ένα χιλιάρικο με κέρματα των 100 δραχμών και των 50 δραχμών. Με πόσους τρόπους μπορεί να γίνει η ανταλλαγή, αν ο οδηγός θέλει οπωσδήποτε και κατοστάρικα και πενηντάρικα;

ΛΥΣΗ

Αν η ανταλλαγή μπορεί να γίνει με x κατοστάρικα και y πενηντάρικα, τότε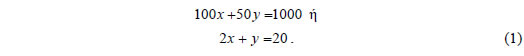

Αναζητούμε προφανώς τις ακέραιες και θετικές λύσεις της (1). Επειδή (2,1)=1 και , η εξίσωση έχει ακέραιες λύσεις. Για να βρούμε το σύνολο των λύσεών της, πρέπει να βρούμε μια μερική λύση (x₀,y₀) της εξίσωσης ή, όπως λέμε, μια ε ι δ ι κ ή λ ύ σ η της εξίσωσης.

Εκφράζουμε γραμμικά το Μ.Κ.Δ. των 2 και 1 και έχουμε

Πολλαπλασιάζουμε τα μέλη της (2) με 20 και έχουμε 2(20)+1(-20)=20 , που σημαίνει ότι(x₀,y₀)=(20, -20) . Επομένως, οι ακέραιες λύσεις της εξίσωσης (1) δίνονται από τους τύπους:

Από τις λύσεις αυτές πρέπει να βρούμε εκείνες για τις οποίες ισχύει , δηλαδή πρέπει να βρούμε πού συναληθεύουν οι ανισώσεις

Από την επίλυση του συστήματος των ανισώσεων προκύπτει ότι . Επομένως, t= -19, -18, -17, -16, -15, -14, -13, -12, -11 και οι αντίστοιχες τιμές των x και y φαίνονται στον παρακάτω πίνακα:

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ
1.	Ποιες από τις παρακάτω εξισώσεις έχουν ακέραιες λύσεις;
2.	Να βρείτε τις ακέραιες λύσεις των εξισώσεων