| 1. |
- Να αποδείξετε την ταυτότητα
α2 + β2 + γ2 - αβ - βγ - γα = $\dfrac{1}{2}$ [(α - β)2 + (β - γ)2 + (γ - α)2].
- Να αποδείξετε ότι για όλους τους α, β, γ ∈ℝ ισχύει
α2 + β2 + γ2≥ αβ + βγ + γα.
Πότε ισχύει ισότητα; |
| 2. |
Λέμε ότι μια τριάδα θετικών ακεραίων (β, γ, α) είναι πυθαγόρεια τριάδα όταν β2 + γ2 = α2 , δηλαδή όταν οι β, γ, α είναι πλευρές ορθογωνίου τριγώνου.
| i. |
Αν (β, γ, α) είναι μια πυθαγόρεια τριάδα και κ είναι ένας θετικόςακέραιος, να αποδείξετε ότι και η τριάδα (κβ, κγ, κα) είναι επίσης πυθαγόρεια τριάδα. |
| ii. |
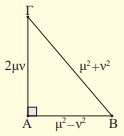
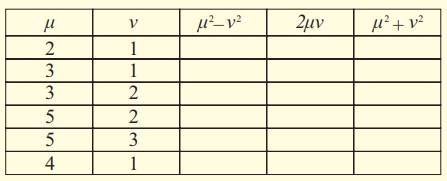
Αν μ και ν θετικοί ακέραιοι με μ>ν, να δείξετεότι η τριάδα (μ2 - ν2, 2μν, μ2 + ν2) είναι πυθαγόρεια τριάδα. Στη συνέχεια να συμπληρώσετετον πίνακα με τις πυθαγόρειες τριάδες που αντιστοιχούν στις τιμές των μ και ν που δίνονται στις δυο πρώτες στήλες: |
 |
| |
 |
|
| 3. |
A) Να αποδείξετε ότι $αβ ≤ \left(\dfrac{α+β}{2}\right)^2$. Τι σημαίνει η ανισότητα αυτή γιαένα ορθογώνιο με διαστάσεις α και β ; Πότε ισχύει η ισότητα;
B) Με τη βοήθεια της παραπάνω ανισότητας (ή και με άλλο τρόπο), να αποδείξετε ότι:
- Από όλα τα ορθογώνια με σταθερή περίμετρο P το τετράγωνο έχειτο μεγαλύτερο εμβαδό.
- Από όλα τα ορθογώνια με σταθερό εμβαδό E το τετράγωνο έχειτην ελάχιστη περίμετρο.
|
| 4. |
Δίνεται η εξίσωση 3(x + 1) - αx = 4, α $\in$ℝ
- Να λύσετε την εξίσωση για τις διάφορες τιμές του α $\in$ℝ.
- Για ποιες τιμές του α $\in$ℝ η εξίσωση έχει λύση μεγαλύτερη του 1;
|
| 5. |
Δίνεται η εξίσωση λ2(χ - 1) + 3λ = χ + 2, λ $\in$ℝ
- Να αποδείξετε ότι η εξίσωση αυτή γράφεται ισοδύναμα:
(λ − 1)(λ + 1) χ = (λ − 1)(λ − 2).
- Να λύσετε την εξίσωση για τις διάφορες τιμές του λ $\in$ℝ.
- Να βρείτε τις τιμές του λ $\in$ℝ για τις οποίες η εξίσωση έχει ρίζα τον αριθμό $\dfrac{1}{2}$ .
|
| 6. |
Από τη φυσική γνωρίζουμε ότι στην κατακόρυφη βολή ενός σώματος με αρχική ταχύτητα ν0 το ύψος h του σώματος συναρτήσει του χρόνου t της κίνησης του δίνεται από τον τύπο $h(t) = v_0t - \dfrac{1}{2}gt^2$, όπου g η επιτάχυνση της βαρύτητας.
| A) |
Αν v0 = 60m/sec και g 10m/sec2 : 10m/sec2 :
- Να βρείτε πότε το σώμα θα φθάσει σε ύψος h =180 μέτρα.
- Να βρείτε πότε το σώμα θα βρεθεί σε ύψος h =100 μέτρα.
Ποια είναι η ερμηνεία των προηγούμενων απαντήσεων; |
| B) |
Στη γενική περίπτωση όπου $h(t) = v_0t - \dfrac{1}{2}gt^2$, με τα v0 και g σταθερά,να βρείτε τη συνθήκη που πρέπει να ισχύει, ώστε το σώμα να φθάσει σεδεδομένο ύψος h0 . |
|
| 7. |
Στο ίδιο σύστημα συντεταγμένων να παραστήσετε γραφικά τις συναρτήσεις
$f(x) = |x| - 2$ και $g(x) = 2 - |x|$
και στη συνέχεια να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τις γραφικές παραστάσεις των συναρτήσεων f και g. |
| 8. |
| A) |
Στο ίδιο σύστημα συντεταγμένων να χαράξετε τις γραφικές παραστάσεις των συναρτήσεων
$f(x) = |x-1|$ και $g(x) = |x-3|$
και με τη βοήθεια αυτών να βρείτε τις λύσεις της ανίσωσης
$|x-1|$ < $|x-3|$. |
| B) |
Στη συνέχεια να επιβεβαιώσετε αλγεβρικά τα προηγούμενα συμπεράσματα. |
|
| 9. |
| A) |
Σε ένα καρτεσιανό επίπεδο να σχεδιάσετε τις γραφικές παραστάσειςτων συναρτήσεων:
$f(x) = |x|$, $g(x) = |x|-3$ και $||x|-3|$. |
| B) |
Με τη βοήθεια των παραπάνω γραφικών παραστάσεων να προσδιορίσετε το πλήθος των λύσεων του συστήματος
$\begin{cases} y= ||x| - 3 | \\ y = α \end{cases}$
για τις διάφορες τιμές του α $\in$ ℝ. |
|
| 10. |
Σε ένα επίπεδο σχεδιάζουμε ένα καρτεσιανό σύστημα συντεταγμένων Oxy.
- Να δείξετε ότι η εξίσωση y2 − x2 = 0 παριστάνει τις διχοτόμους δ1και δ2 των γωνιών των αξόνων τις οποίες και να σχεδιάσετε.
- Ποια είναι η απόσταση ενός σημείου M (x, y) του επιπέδου από τοσημείο K (α, 0) του άξονα x′x ; Να δείξετε ότι η εξίσωση(x − α)2 + y2 = 1, α $\in$ ℝ παριστάνει στο επίπεδο κύκλο C με κέντρο K και ακτίνα 1.Σχεδιάστε τον κύκλο για μια τιμή του α.
- Με τη βοήθεια των παραπάνω γραφικών παραστάσεων να προσδιορίσετε το πλήθος των λύσεων του συστήματος
$\begin{cases} y^2 - x^2 = 0\\ (x-α)^2 + y^2 = 1 \end{cases}$
για τις διάφορες τιμές του α $\in$ ℝ .
|
| 11. |
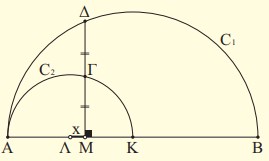
| Στο διπλανό σχήμα τα C1 καιC2 είναι ημικύκλια με κέντρα Κ και Λ και ακτίνες R1 = 6cm και R2 = 3cm αντιστοίχως, ενώ το Μ είναι ένα σημείο της διακέντρου ΚΛ και η ΜΔ είναικάθετη στην ΚΛ. Να βρείτε το μήκος x του τμήματος ΛΜ, αν γνωρίζουμε ότι το σημείο Γ είναι μέσο του ΜΔ. |
 |
|
| 12. |
Θεωρούμε έναν άξονα x'x και παίρνουμε πάνω σ' αυτόν τα σταθεράσημεία Α(−1) , Β(1) και ένα μεταβλητό σημείο Μ( x) . Θέτουμε
f(x) = (MA) + (MB) και g(x) = |(MA) - (MB)|.
- Να αποδείξετε ότι:
$f(x) = |x+1| + |x-1|$ και $g(x) = ||x+1| - |x-1||$.
- Να παραστήσετε γραφικά τις συναρτήσεις f και g.
- Να βρείτε με τη βοήθεια των παραπάνω γραφικών παραστάσεων τηνελάχιστη και τη μέγιστη τιμή (εφόσον υπάρχουν) των συναρτήσεων fκαι g, καθώς και τις θέσεις στις οποίες παρουσιάζονται.
|
| 13. |
Στα παρακάτω σχήματα δίνονται οι γραφικές παραστάσεις των συναρτήσεων:
$f(x) = \dfrac{2}{x^2 + 1}$, $g(x) = \dfrac{4x}{x^2+1}$ & $h(x) = \dfrac{4x^2}{x^4 + 1}$
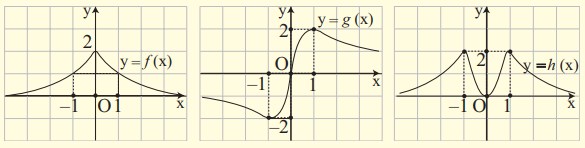
- Από τις γραφικές παραστάσεις να βρείτε τα ολικά ακρότατα των συναρτήσεων
 , g, h, καθώς και τις θέσεις των ακροτάτων αυτών. , g, h, καθώς και τις θέσεις των ακροτάτων αυτών.
- Να επιβεβαιώσετε αλγεβρικά τα προηγούμενα συμπεράσματα.
|
| 14. |
| A) |
Δίνεται η συνάρτηση $f(x) = \sqrt{x}$.
- Να βρείτε το πεδίο ορισμού της συνάρτησης f.
- Να αποδείξετε ότι αν το σημείο M(α, β) ανήκει στη γραφική παράσταση της f, το σημείο M '(α, β) ανήκει στη γραφική παράσταση της συνάρτησης g (x) = x2 .
- Στο ίδιο σύστημα αξόνων να σχεδιάσετε πρώτα τη γραφική παράσταση της συνάρτησης g και στη συνέχεια, με τη βοήθεια τουπροηγούμενου ερωτήματος, να σχεδιάσετε τη γραφική παράστασητης συνάρτησης f. Ποιο είναι το είδος της μονοτονίας και ποιο τοακρότατο της συνάρτησης f;
|
| B) |
Να δείξετε ότι η συνάρτηση $h(x) = \sqrt{|x|}$ είναι άρτια και στη συνέχειανα χαράξετε τη γραφική της παράσταση. |
| Γ) |
Στο παρακάτω σχήμα δίνεται η γραφική παράσταση της $f(x) = \sqrt{x}$.
Αν Α', Β', Γ ' , …, Μ ', Ν ' είναι τα σημεία της γραφικής παράστασης τηςf με τετμημένες 1, 2, 3,…, ν, ν +1 αντιστοίχως, να αποδείξετε ότι τα τρίγωνα 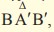 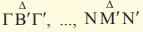 είναι ισοσκελή. είναι ισοσκελή. |
|
| 15. |
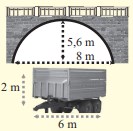
| Μία γέφυρα έχει ένα παραβολικό τόξο του οποίου το πλάτος είναι 8m και ύψος είναι 5,6m. Κάτω από τη γέφυρα θέλει να περάσει γεωργικό μηχάνημα του οποίου η καρότσα έχει πλάτος 6m και ύψος 2m. Μπορεί το μηχάνημα να περάσει; |
 |
|
| 16. |
Δίνεται ένα τετράγωνο ΑΒΓΔ με πλευρά 20cm και το μέσον Ο της ΑΔ.Ένα κινητό σημείο Μ ξεκινά από το Α και, διαγράφοντας την πολυγωνική γραμμή ΑΒΓΔ, καταλήγει στο Δ.
Αν με x συμβολίσουμε το μήκος της διαδρομής που έκανε το κινητό Μκαι με f(x) το εμβαδόν του σκιασμένου χωρίου,
- Να βρείτε το πεδίο ορισμού και τον τύπο της συνάρτησης f.
- Να παραστήσετε γραφικά την f.
- Να βρείτε την τιμή του x για την οποία ισχύει f(x) = 120 cm2.
|
| 17. |
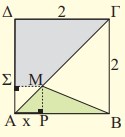
Στο διπλανό σχήμα το ΑΒΓΔ είναι τετράγωνοπλευράς 2 μ. και το M είναι ένα σημείο της διαγωνίου ΑΓ με (ΑΡ) = x . Συμβολίζουμε με
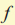 ( x) το εμβαδόν του τριγώνου ΜΑΒ και με ( x) το εμβαδόν του τριγώνου ΜΑΒ και με
g (x) το εμβαδόν του τραπεζίου ΜΓΔΣ . |
 |
- Να αποδείξετε ότι
$f(x) = x,$ $ 0≤ x ≤ 2$ και $g(x) = -0,5x^2 + 2, $ $ 0≤ x ≤ 2$.
- Να βρείτε τις τιμές του x για τις οποίες τα δύο εμβαδά είναι ίσα.
- Να παραστήσετε γραφικά στο ίδιο σύστημα συντεταγμένων τις συναρτήσεις f και g και να βρείτε, με τη βοήθεια των γραφικών παραστάσεων, με προσέγγιση την τιμή του x για την οποία τα δύο εμβαδά είναι ίσα.
|
|
| 18. |
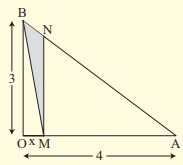
| Στο διπλανό σχήμα το τρίγωνο ΟΑΒ είναιορθογώνιο, το Μ είναι τυχαίο σημείο τηςΟΑ και ΜΝ//ΟΒ. Αν (ΟΑ)=4, (ΟΒ)=3 και(ΟΜ)=x, και Ε(x) είναι το εμβαδόν του τριγώνου ΒΜΝ,
|
 |
- Να αποδείξετε ότι
$(MN) = \dfrac{3(4-x)}{4}$ και $E(x) = -\dfrac{3}{8}x^2 + \dfrac{3}{2}x.$
- Να βρείτε τη θέση του Μ για την οποία το εμβαδόν E(x) μεγιστοποιείται. Ποια είναι η μέγιστη τιμή του E(x).
|
|
| 19. |
| Σε ένα καρτεσιανό επίπεδο θεωρούμε τα σημεία A(0,4) και B(2,2) , καθώς και το σημείο M(x,0) που κινείται κατά μήκος του άξονα x ' x .
|
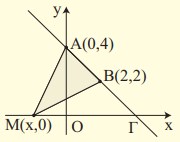 |
- Να βρείτε τις συντεταγμένες του σημείου Γ στο οποίο τέμνει η ευθεία ΑΒτον άξονα x ' x .
- Να εκφράσετε το εμβαδόν του τριγώνου
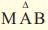 συναρτήσει της τετμημένης x του σημείου Μ και να παραστήσετε γραφικά τη συνάρτηση αυτή. συναρτήσει της τετμημένης x του σημείου Μ και να παραστήσετε γραφικά τη συνάρτηση αυτή.
|
|
| 20. |
Σε ένα τμήμα ΑΒ = 10km μιας λεωφόρου πέφτει συνεχώς χιόνι και τούψος του χιονιού αυξάνεται 1cm την ώρα. Όταν αρχίζει η χιονόπτωσηένα εκχιονιστικό μηχάνημα αρχίζει από το άκρο Α να καθαρίζει το χιόνικινούμενο κατά μήκος του δρόμου με ταχύτητα 10km/h . Μόλις φτάσειστο Β γυρίζει και καθαρίζει το δρόμο αντιστρόφως από το Β προς το Ακαι συνεχίζει με τον ίδιο τρόπο.
- Να σχεδιάσετε ένα διάγραμμα για το ύψος του χιονιού στο Α , παραβλέποντας το χρόνο στροφής στα Α και Β.
- Να κάνετε το ίδιο για το ύψος του χιονιού στο μέσο Μ του ΑΒ.
|
| 21. |
Έστω ο δειγματικός χώρος Ω = {0, 1, 2, 3,..., 100}. Δίνονται και οιπιθανότητες $P(κ) = \dfrac{1}{2^κ}$ κ = 1, 2,..., 100. Να υπολογίσετε την πιθανότητα P(0). |
| 22. |
Έστω Ω ένας δειγματικός χώρος με πεπερασμένο πλήθος στοιχείων και Α, Β υποσύνολα του Ω. Υποθέτουμε ότι P(A')≤0,28 καιP(B')≤0,71. Να αποδείξετε ότι i) P(A∩B)≥1,01− P(A∪B) και ii)A∩B≠∅. |