Γεωμετρικά σχήματα – Η περίμετρος

46

Διερεύνηση

Συζητάμε τα είδη των γραμμών που αναγνωρίζουμε στην παραπάνω ζωγραφιά των μαθητών και των μαθητριών της Ε΄τάξης.

Στο χαρτί με τις τελείες σχεδιάζουμε κλειστές τεθλασμένες γραμμές και φτιάχνουμε διάφορα γεωμετρικά σχήματα:

Συζητάμε:

α. σε ποιες ομάδες μπορούμε να διακρίνουμε τα γεωμετρικά σχήματα, αν μετρήσουμε το πλήθος των κορυφών τους,

β. τι μετράμε, αν προσθέσουμε τα μήκη όλων των πλευρών κάθε γεωμετρικού σχήματος.

Γεωμετρικά σχήματα – Η περίμετρος

Ενότητα 8

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
Το σχήμα που φτιάχνεται από μια κλειστή τεθλασμένη γραμμή και οι πλευρές του τέμνονται μόνο σε σημεία που είναι κορυφές του ονομάζεται πολύγωνο.
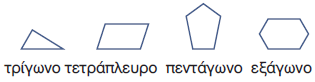
Το τρίγωνο, το τετράπλευρο, το πεντάγωνο και το εξάγωνο είναι πολύγωνα με τρεις, τέσσερις, πέντε και έξι κορυφές αντίστοιχα.
Ένα πολύγωνο ονομάζεται κανονικό, όταν έχει όλες τις πλευρές του ίσες και όλες τις γωνίες του ίσες.
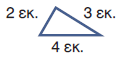
Περίμετρος (Π) ενός πολυγώνου είναι το άθροισμα των μηκών των πλευρών του.		Πτρ. = 2 εκ. + 3 εκ. + 4 εκ. = 9 εκ.

Εφαρμογή

Να βρείτε τις περιμέτρους: α. ενός ισόπλευρου τριγώνου, β. ενός τετραγώνου, γ. ενός κανονικού πενταγώνου και δ. ενός κανονικού εξαγώνου, καθένα από τα οποία έχει μήκος πλευράς 4,5 εκ. Να γράψετε το συμπέρασμά σας.
Επειδή η περίμετρος είναι το άθροισμα των μηκών των πλευρών κάθε πολυγώνου και κάθε κανονικό πολύγωνο έχει όλες τις πλευρές του ίσες, οι περίμετροί τους είναι:

Επομένως, για να βρούμε την περίμετρο ενός κανονικού πολυγώνου, ................................... το μήκος της πλευράς .......................................................................

Μικροπείραμα Ανοιχτή δραστηριότητα Μικροπείραμα Μικροπείραμα
Μικροπείραμα Μικροπείραμα

Αναστοχασμός

Εξηγούμε γιατί το ισόπλευρο τρίγωνο και το τετράγωνο είναι κανονικά πολύγωνα.
Η Δανάη υποστηρίζει ότι όλα τα εξάγωνα είναι κανονικά. Έχει δίκιο ή όχι και γιατί;
Εξηγούμε γιατί το ορθογώνιο και ο ρόμβος δεν είναι κανονικά πολύγωνα.
Ο Νίκος θέλει να σχεδιάσει ένα τετράγωνο, ένα ισόπλευρο τρίγωνο και ένα κανονικό εξάγωνο, καθένα από τα οποία έχει περίμετρο 24 εκ. Πώς θα υπολογίσει το μήκος της πλευράς του κάθε σχήματος;