
Σχεδιάζουμε στο παρακάτω τετραγωνισμένο χαρτί ένα τετράγωνο με πλευρά 1 εκ.

Πόσα τέτοια τετράγωνα έχει το τετραγωνισμένο χαρτί της παραπάνω εικόνας;
.............................................................................................................................................................
Υπολογίζουμε πόσα τετράγωνα με πλευρά 1 χιλ. έχουν:
α. το τετράγωνο που σχεδιάσαμε
.............................................................................................................................................................
β. το τετραγωνισμένο χαρτί της εικόνας
.............................................................................................................................................................

| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Εμβαδό ενός επίπεδου σχήματος είναι ο αριθμός που εκφράζει το αποτέλεσμα της σύγκρισής του με ένα άλλο επίπεδο σχήμα το οποίο θεωρούμε μονάδα μέτρησης. |
|
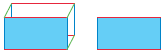
Η σκιασμένη επιφάνεια του σώματος είναι 6 τ.εκ. ή έχει εμβαδό 6 τ.εκ. |
| Βασική μονάδα μέτρησης της επιφάνειας είναι το τετραγωνικό μέτρο (τ.μ.), που είναι ένα τετράγωνο με μήκος πλευράς 1 μ. Α. Υποδιαιρέσεις του τετραγωνικού μέτρου είναι:
|
|
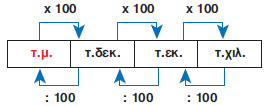
1 τ.μ. = 100 τ.δεκ. ή 1 τ.δεκ.= $\dfrac{1}{100}$ τ.μ. 1 τ.δεκ. = 100 τ. εκ. ή 1 τ.εκ.= $\dfrac{1}{100}$ τ.δεκ. 1 τ.εκ. = 100 τ.χιλ. ή 1 τ.χιλ.= $\dfrac{1}{100}$ τ.εκ. |
Β. Πολλαπλάσια του τετραγωνικού μέτρου είναι:
|
|
1 τ.χμ. = 1.000 στρέμ. 1 στρέμ. = 1.000 τ.μ. |
| Για να μετατρέψουμε μία μονάδα μέτρησης της επιφάνειας στην αμέσως μικρότερή της, πολλαπλασιάζουμε με το 100, ενώ στην αμέσως μεγαλύτερή της, διαιρούμε με το 100. |
|
|

Μέσα στο οικόπεδο του κυρίου Γιάννη, το οποίο έχει επιφάνεια 2 στρέμ., θα κατασκευαστεί ένας δρόμος επιφάνειας 200 τ.μ., που θα το χωρίσει σε δύο οικόπεδα το ένα διπλάσιας επιφάνειας από το άλλο. Να βρείτε πόσο θα είναι το εμβαδό κάθε οικοπέδου μετά την κατασκευή του δρόμου.
H επιφάνεια του αρχικού οικοπέδου είναι 2 στρέμ.= 2 x 1.000 τ.μ. = 2.000 τ.μ.
Η επιφάνεια των δύο οικοπέδων θα είναι: 2.000 - 200 = 1.800 τ.μ. Επειδή το ένα οικόπεδο θα έχει διπλάσια επιφάνεια από το άλλο, η επιφάνεια των δύο οικοπέδων θα αποτελείται από τρία ίσα μέρη. Επομένως 1.800 : 3 = 600 τ.μ. θα είναι η επιφάνεια του ενός οικοπέδου και 2 x 600 = 1.200 τ.μ. του άλλου.
