2.2 Τριγωνομετρικοί αριθμοί παραπληρωματικών γωνιών

Γνωρίζω ποια σχέση συνδέει:

Τους τριγωνομετρικούς αριθμούς παραπληρωματικών γωνιών
Τις γωνίες που έχουν το ίδιο ημίτονο. .

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

Σε ορθοκανονικό σύστημα αξόνων Oxy να πάρετε το σημείο Μ(3, 4).

1. Ποιες είναι οι συντεταγμένες του σημείου Μ΄, που είναι συμμετρικό του Μ ως προς τον άξονα y΄y;

2. Να εξηγήσετε γιατί οι γωνίες x$\hat{O}$M = ω και x$\hat{O}$M΄ = φ είναι παραπληρωματικές.

3. Να βρείτε τους τριγωνομετρικούς αριθμούς των γωνιών ω και φ και τη σχέση που τους συνδέει.

Μικροπείραμα

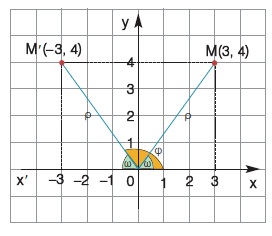
Σε ορθοκανονικό σύστημα αξόνων Oxy παίρνουμε το σημείο Μ(3, 4) και βρίσκουμε το συμμετρικό του σημείο Μ΄(-3, 4) ως προς τον άξονα y΄y. Αν ονομάσουμε ω τη γωνία xÔM, τότε λόγω συμμετρίας είναι x΄ÔM΄ = ω, οπότε για τη γωνία φ = xÔM΄ ισχύει φ = 180º - ω, που σημαίνει ότι οι γωνίες ω και φ είναι παραπληρωματικές, αφού ω + φ = 180º. Έχουμε ακόμη ότι ρ = OM = OM΄ = √9+16 = √25 = 5, οπότε:

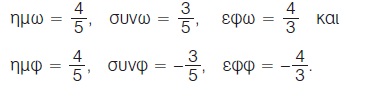
εικόνα

Παρατηρούμε λοιπόν, ότι:

Οι παραπληρωματικές γωνίες ω, φ = 180º - ω έχουν το ίδιο ημίτονο και αντίθετους τους άλλους τριγωνομετρικούς αριθμούς.

Γενικά

Για δύο παραπληρωματικές γωνίες ω και 180º − ω ισχύουν:

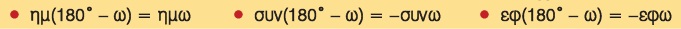
Με τους προηγούμενους τύπους μπορούμε να υπολογίσουμε τους τριγωνομετρικούς αριθμούς μιας γωνίας, αν γνωρίζουμε τους τριγωνομετρικούς αριθμούς της παραπληρωματικής της.

Για παράδειγμα,

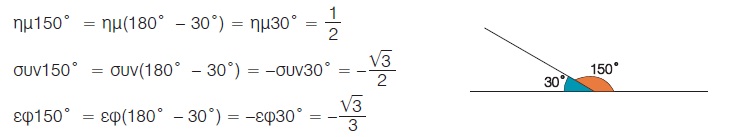
εικόν

Στο προηγούμενο παράδειγμα βλέπουμε ότι οι παραπληρωματικές γωνίες 150º και 30º, αν και δεν είναι ίσες, έχουν το ίδιο ημίτονο. Επομένως:

Αν δύο γωνίες έχουν το ίδιο ημίτονο και είναι από 0º μέχρι και 180º, τότε είναι ίσες ή παραπληρωματικές.

Για παράδειγμα, αν ημχ = ημ35^o και 0 ≤ x ≤ 180º, τότε είναι x = 35º ή x = 180º - 35º, δηλαδή χ = 35º ή χ = 145º.

ΠΑΡΑΔΕΙΓΜΑΤΑ− ΕΦΑΡΜΟΓΕΣ

Να υπολογιστεί η τιμή της παράστασης Α = ημ140º + συν170º - ημ40º + συν10º.

Λύση

Οι γωνίες 140º και 40º είναι παραπληρωματικές, οπότε θα έχουν το ίδιο ημίτονο, δηλαδή είναι ημ140º = ημ40º.

Οι γωνίες 170º και 10º είναι παραπληρωματικές, οπότε θα έχουν αντίθετα συνημίτονα, δηλαδή είναι συν170º = − συν10º.

Άρα: Α = ημ140º + συν170º - ημ40º + συν10º = ημ40º - συν10º - ημ40º + συν10º = 0.

εικόνα

Λύση

Οι γωνίες εικόνα , , του τριγώνου έχουν άθροισμα 180^o, δηλαδή είναι: 80º + 70º + = 180º, οπότε = 30º. Άρα:

α) ημ(Α + Β) = ημ(80º + 70º) = ημ150º = ημ(180º - 30º) = ημ30^o = ημΓ.

β) συν(Α + Β) = συν(80º + 70º) = συν150º = συν(180º - 30º) = -συν30º = -συνΓ.

Μικροπείραμα

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

Να χαρακτηρίσετε τις παρακάτω ισότητες με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες:

α) ημ150º = ημ30º
β) συν135º = συν45º
γ) εφ100º = εφ80º
δ) εφ75º = -εφ105º.
ε) συν110º = -συν70º
στ) ημ140º = -ημ40º

Αν για τη γωνία x ισχύει 0 ≤ x ≤180º, να συμπληρώσετε τις παρακάτω προτάσεις:

α) Αν ημx = ημ60º, τότε x = .............

β) Αν συνx = -συν20º, τότε x = .........

γ) Αν εφx = -εφ30º, τότε x = ............

Να συμπληρώσετε τον παρακάτω πίνακα αντιστοιχίζοντας σε κάθε τριγωνομετρικό αριθμό της στήλης Α τον ίσο του τριγωνομετρικό αριθμό από τη στήλη Β.

Στήλη Α		Στήλη Β
		1.	ημ40º
α.	ημ140º	2.	συν40º
β.	συν140º	3.	εφ40º
γ.	εφ140º	4.	-ημ40º
		5.	-συν40º
		6.	-εφ40º

α	β	γ

ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ − ΠΡΟΒΛΗΜΑΤΑ

Να υπολογίσετε τους τριγωνομετρικούς αριθμούς των γωνιών:

α) 120º

β) 135º

γ) 150º

Μικροπείραμα

Να αποδείξετε ότι:

α) ημ108º + συν77º - ημ72º + συν103º = 0

β) εφ122º - εφ58º·εφ135º = 0

Να αποδείξετε ότι:

α) συν²45º + συν²135º = 1

β) ημ²30º + ημ²60º + ημ²120º + ημ²150º = 2

Να αποδείξετε ότι: ημ(140º + x) = ημ(40º - x) και συν(158º - x) = -συν(22º + x).

Να βρείτε τη γωνία x, όταν:

εικόνα

Να αποδείξετε ότι οι γωνίες ενός παραλληλογράμμου έχουν το ίδιο ημίτονο. Ισχύει το ίδιο και για τα συνημίτονα των γωνιών του;

Δίνεται τετράπλευρο ΑΒΓΔ με Να αποδείξετε ότι:
α) ημΑ + συνΑ - ημΓ + συνΓ = 0 β) εφΑ + εφΓ = 0

Μικροπείραμα

Στο ορθογώνιο τρίγωνο ΑΒΓ του διπλανού σχήματος να υπολογίσετε τους τριγωνομετρικούς αριθμούς των γωνιών ω και φ.

Δίνεται ισόπλευρο τρίγωνο ΑΒΓ με πλευρά 6 cm και σημείο Δ της πλευράς ΒΓ τέτοιο, ώστε ΒΔ = 2 cm. Να υπολογίσετε τους τριγωνομετρικούς αριθμούς των γωνιών ω και φ.

Μικροπείραμα