2.1 Τριγωνομετρικοί αριθμοί γωνίας με 0º ≤ω ≤ 180º

εικονα

Θυμάμαι πως ορίζονται οι τριγωνoμετρικοί αριθμοί οξείας γωνίας ορθογωνίου τριγώνου.
Γνωρίζω πως ορίζονται οι τριγωνομετρικοί αριθμοί γωνίας ω με 0º ≤ω ≤ 180º
Μαθαίνω να υπολογίζω τους τριγωνομετρικούς αριθμούς μιας γωνίας με τη βοήθεια ενός ορθοκανονικού συστήματος αξόνων.

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

Σε ένα ορθοκανονικό σύστημα αξόνων Oxy φέραμε την ημιευθεία OM, που σχηματίζει με τον ημιάξονα Ox γωνία ω.

1. Να προσδιορίσετε τις συντεταγμένες του σημείου M και να υπολογίσετε την απόσταση του M από την αρχή O.

2. Να βρείτε τους τριγωνομετρικούς αριθμούς της γωνίας ω.

Μικροπείραμα

Στην προηγούμενη τάξη μάθαμε πώς ορίζονται οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορθογωνίου τριγώνου, του οποίου γνωρίζουμε τις πλευρές του. Συγκεκριμένα, μάθαμε ότι:

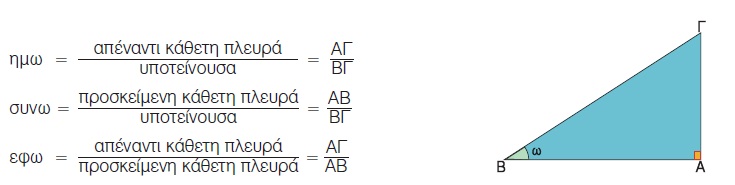
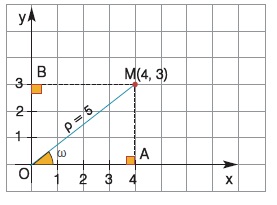
εικονα

Οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορίζονται και με τη βοήθεια ενός ορθοκανονικού συστήματος αξόνων. Αν σ' ένα ορθοκανονικό σύστημα αξόνων Oxy πάρουμε το σημείο M(4, 3) και φέρουμε ΜΑ ⊥ x΄x και ΜΒ ⊥ y΄y, τότε έχουμε OA = 4 και OB = ΑΜ = 3. Οι τριγωνομετρικοί αριθμοί της γωνίας
ω = x Ô M υπολογίζονται από το ορθογώνιο τρίγωνο OAM. Από το Πυθαγόρειο θεώρημα στο τρίγωνο αυτό για την απόσταση ρ =OM έχουμε ρ² = 4² + 3²,

εικόνα

Με τη βοήθεια όμως ενός ορθοκανονικού συστήματος αξόνων μπορούμε να ορίσουμε τους τριγωνομετρικούς αριθμούς μιας γωνίας ω και όταν αυτή δεν είναι οξεία. Αν έχουμε μία αμβλεία γωνία ω, τότε την τοποθετούμε σ' ένα ορθοκανονικό σύστημα αξόνων Oxy, έτσι ώστε η κορυφή της να συμπέσει με την αρχή O, η μία πλευρά της να συμπέσει με τον θετικό ημιάξονα Ox και η άλλη της πλευρά να βρεθεί στο 2ο τεταρτημόριο. Αν στην πλευρά αυτή πάρουμε ένα οποιοδήποτε σημείο M(x, y), διαφορετικό από το O, τότε για την απόσταση ρ = OM ισχύει

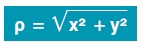
Οι τριγωνομετρικοί αριθμοί της γωνίας ω είναι:

εικόνα

Μικροπείραμα

Παρατηρούμε ότι:

Αν η γωνία ω είναι οξεία, τότε είναι x>0, y>0, ρ>0, οπότε: ημω>0, συνω>0, εφω>0.
Αν η γωνία ω είναι αμβλεία, τότε είναι x<0, y>0, ρ>0, οπότε: ημω>0, συνω<0, εφω<0.

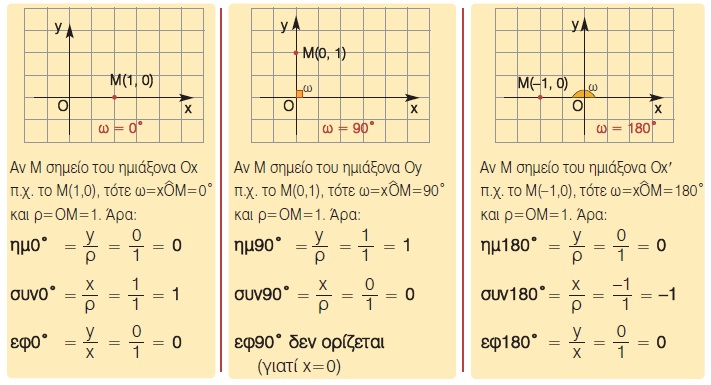
Οι προηγούμενοι τύποι γενικεύονται και όταν ω = 0º ή ω = 90º ή ω = 180º.

Έτσι, μπορούμε τώρα να υπολογίσουμε και τους τριγωνομετρικούς αριθμούς των γωνιών 0º, 90º και 180º.

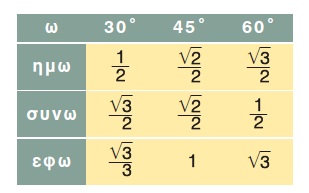
εικόνα

Υπενθυμίζουμε και τους τριγωνομετρικούς αριθμούς των γωνιών 30º, 45º και 60º που φαίνονται στον διπλανό πίνακα.

ΠΑΡΑΔΕΙΓΜΑΤΑ − ΕΦΑΡΜΟΓΕΣ

Σε ορθοκανονικό σύστημα αξόνων Oxy παίρνουμε το σημείο Μ(-4, 3). Να υπολογιστούν οι τριγωνομετρικοί αριθμοί της γωνίας ω = xÔM.

Λύση

Σε ορθοκανονικό σύστημα αξόνων Oxy φέρουμε ημιευθεία Oz, ώστε xÔz = 135º. Πάνω στην Oz παίρνουμε το σημείο Μ με τετμημένη -1. Να υπολογιστούν οι τριγωνομετρικοί αριθμοί της γωνίας xÔ Μ = 135º.

Λύση

Φέρνουμε ΜΒ ⊥ x΄x και ΜΓ ⊥ y΄y. Επειδή χÔΜ = 135º και xOy = 90º θα είναι ΓΟΜ = 45º, οπότε το ορθογώνιο τρίγωνο ΟΜΓ είναι και ισοσκελές. Άρα ΟΓ = ΜΓ = ΟΒ = 1 και η τεταγμένη του σημείου Μ είναι y = 1.

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

Για το σημείο Μ(5, 12) είναι ρ = ΟΜ = 13. Αν ω = xÔΜ να συμπληρώσετε τις παρακάτω ισότητες:

ημω = .......

συνω = .......

εφω = .......

Αν η γωνία ω = xÔM είναι αμβλεία, τότε να συμπληρώσετε τα παρακάτω κενά με το σύμβολο > ή <.

ημω .... 0

συν .... 0

εφω .... 0

Να συμπληρώσετε τον παρακάτω πίνακα αντιστοιχίζοντας σε κάθε τριγωνομετρικό αριθμό της στήλης Α τον ίσο του αριθμό από τη στήλη Β.

Στήλη Α		Στήλη Β
α.	ημ90º
β.	συν180º
γ.	εφ0º	1.	0
δ.	συν90º	2.	-1
ε.	ημ0º	3.	1
στ.	εφ180º
ζ.	συν0º
η.	. ημ180º

α	β	γ	δ	ε	στ	ζ	η

Να χαρακτηρίσετε τις παρακάτω προτάσεις με (Σ), αν είναι σωστές ή με (Λ), αν είναι λανθασμένες.

α) Για κάθε γωνία ω ισχύει -1 ≤ συνω ≤1.
β) Αν η γωνία ω είναι αμβλεία, τότε εφω < 0.
γ) Αν για τη γωνία ω ισχύει ημω > 0, τότε η ω είναι οξεία.
δ) Το ημίτονο οποιασδήποτε γωνίας τριγώνου είναι θετικός αριθμός.

ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ − ΠΡΟΒΛΗΜΑΤΑ

Να υπολογίσετε τους τριγωνομετρικούς αριθμούς της γωνίας ω = χÔΜ, όταν:

α) M(3, 4)

β) M(-5, 12)

γ) M(0, 3)

Μια ευθεία ε έχει εξίσωση y = -2x.

α) Να σχεδιάσετε την ευθεία ε και να προσδιορίσετε την τεταγμένη ενός σημείου της M που έχει τετμημένη -1.

β) Να υπολογίσετε τους τριγωνομετρικούς αριθμούς της γωνίας ω = xÔM.

Μικροπείραμα

Ένα πλοίο Π αναχώρησε από το λιμάνι Ο και κινήθηκε βορειοανατολικά προς μία κατεύθυνση που σχημάτιζε με τον άξονα Οx γωνία 30^o. Να βρείτε τις συντεταγμένες του πλοίου μετά από διαδρομή 10 μιλίων.

Μικροπείραμα

Στο διπλανό σχήμα το τρίγωνο ΟΒΜ είναι ισόπλευρο. Να υπολογίσετε:

α) τις συντεταγμένες του Μ.

β) τους τριγωνομετρικούς αριθμούς της γωνίας 120º.

Στο διπλανό σχήμα το τρίγωνο ΟΒΜ είναι ισοσκελές.

α) Να αποδείξετε ότι οι συντεταγμένες του Μ είναι (- √3 , 1).

β) Να υπολογίσετε τους τριγωνομετρικούς αριθμούς της γωνίας 150º.

Στο διπλανό σχήμα είναι εφω = . Αν η τετμημένη του σημείου Μ είναι -1, τότε να υπολογίσετε:

α) την τεταγμένη του σημείου Μ.

β) το ημω και το συνω.

Ένα πυροβόλο όπλο βρίσκεται στη θέση Ο και έχει στρέψει την κάννη στο στόχο Σ₁. Αν ο στόχος Σ₁ μετακινηθεί στη θέση Σ₂, τότε να υπολογίσετε πόσες μοίρες πρέπει να στραφεί η κάννη του πυροβόλου όπλου για να σημαδεύει το στόχο στη νέα του θέση;

(Να χρησιμοποιήσετε τριγωνομετρικούς πίνακες).

Μικροπείραμα