4.3 Σταθερά χημικής ισορροπίας Kc

4.3 Σταθερά χημικής ισορροπίας Κ_c - Κ_p

Γενικά

Δύο βασικά ερωτήματα που αφορούν τη χημική αντίδραση είναι:
α. Πόσο γρήγορα ή αργά φτάνει μια χημική αντίδραση στην κατάσταση χημικής ισορροπίας;
β. Αν γνωρίζουμε την αρχική σύσταση του αντιδρώντος συστήματος, τις αρχικές δηλαδή ποσότητες των ουσιών που συμμετέχουν στην αντίδραση, προς τα πού θα οδηγηθεί η αντίδραση και ποια θα είναι η τελική της σύσταση; Ποιες θα είναι δηλαδή οι συγκεντρώσεις αντιδρώντων και προϊόντων στη θέση χημικής ισορροπίας;
Την απάντηση στο πρώτο ερώτημα δίνει η χημική κινητική, ενώ το κλειδί για την απάντηση στο δεύτερο ερώτημα αποτελεί μία σταθερά, που ονομάζεται σταθερά χημικής ισορροπίας.

Σταθερά χημικής ισορροπίας - Κ_c

Για μια αμφίδρομη χημική αντίδραση που περιγράφεται από τη χημική εξίσωση:

αΑ(g) + βΒ(g) ⇌ γΓ(g) + δΔ(g)

αποδεικνύεται ότι στην κατάσταση χημικής ισορροπίας η παράσταση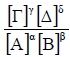

έχει μια σταθερή τιμή που συμβολίζεται με Κ_c. Η σταθερά αυτή ονομάζεται σταθερά χημικής ισορροπίας και μεταβάλλεται μόνο με τη θερμοκρασία. Η παραπάνω σχέση μεταξύ των συγκεντρώσεων των αντιδρώντων και προϊόντων εκφράζει το νόμο χημικής ισορροπίας.

• Η συγκέντρωση του στερεού παραλείπεται από την έκφραση της Κc, καθώς αυτή είναι ανεξάρτητη από την ποσότητά του.

Δηλαδή για την ισορροπία:
CaCO₃(s) ⇌ CaO(s)+ CO₂(g)
έχουμε
Κc = [CO₂]
Επίσης για την ισορροπία:
PCl₅(l) ⇌ PCl₃(l) + Cl₂(g)
Κc = [Cl₂]

Είναι προφανές ότι, όσο μεγαλύτερη είναι η τιμή της Κ_c τόσο μεγαλύτερο ποσοστό των αντιδρώντων μετατρέπεται σε προϊόντα, δηλαδή τόσο περισσότερο η χημική ισορροπία είναι μετατοπισμένη προς τα δεξιά και όσο μικρότερη είναι η τιμή της Κ_c τόσο περισσότερο η χημική ισορροπία είναι μετατοπισμένη προς τα αριστερά.

Κινητική απόδειξη του νόμου χημικής ισορροπίας

Έστω η αμφίδρομη αντίδραση:

2A(g) + B(g) ⇌ A₂B(g)

η οποία λαμβάνει χώρα σε ένα στάδιο και προς τις δύο κατευθύνσεις, είναι δηλαδή απλή αντίδραση και προς τις δύο κατευθύνσεις. Με βάση το νόμο της ταχύτητας, η ταχύτητα της αντίδρασης προς τα δεξιά είναι: υ₁ = k₁[A]²[B],
και αντίστοιχα προς τα αριστερά είναι: υ₂ = k₂[A₂B].
Στην ισορροπία όμως έχουμε: υ₁ = υ₂ οπότε,
k₁[A]²[B] = k₂[A₂B] ή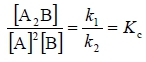
Εικόνα

Σταθερά χημικής ισορροπίας – Κ_p

Αν στο σύστημα ισορροπίας συμμετέχουν αέρια, τότε ο νόμος χημικής ισορροπίας μπορεί να εκφραστεί σε συνάρτηση με τις μερικές πιέσεις των αερίων. Η αντίστοιχη σταθερά συμβολίζεται Κ_p και εξαρτάται μόνο από τη θερμοκρασία. Δηλαδή για τη χημική εξίσωση:

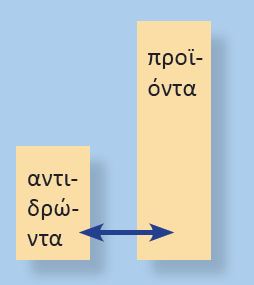Αν η τιμή της σταθεράς χημικής ισορροπίας έχει μεγάλη τιμή, τότε η απόδόση της αντίδρασης είναι μεγάλη.

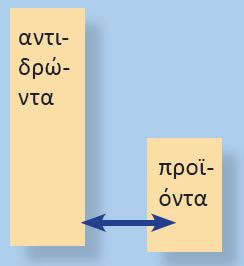Αν η τιμή της σταθεράς χημικής ισορροπίας έχει μικρή τιμή ,τότε η απόδόση της αντίδρασης είναι μικρή.

N₂(g) + 3H₂(g) ⇌ 2NH₃(g)

έχουμε: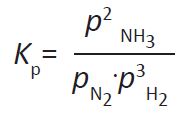

Σχέση που συνδέει την K_p με την K_c

Δίνεται η χημική εξίσωση:

α Α(g) + β B(g) ⇌ γ Γ(g) + δ Δ(g)

H K_p δίνεται από τη σχέση:

Εικόνα

δηλαδή,

K_p = K_c(RT)^Δn

όπου, Δ_n = γ+δ – (α+β),

Αν Δ_n = 0, τότε K_p = K_c Στην περίπτωση αυτή η K_c και η K_p είναι
καθαροί αριθμοί.

Προς ποια κατεύθυνση κινείται μια αντίδραση;

Έστω η ισορροπία: αΑ(g) + βΒ(g) ⇌ γΓ(g) + δΔ(g)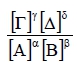
Στη θέση χημικής ισορροπίας η τιμή του κλάσματος

ισούται με K_c. Το παραπάνω κλάσμα, που ονομάζεται πηλίκο αντίδρασης και συμβολίζεται με Q_c, έχει τιμή διάφορο της K_c σε κατάσταση μη ισορροπίας. Με βάση την τιμή της Q_c μπορούμε να προβλέψουμε προς ποια κατεύθυνση οδεύει μια αντίδραση (δεξιά ή αριστερά), ώστε να αποκατασταθεί η ισορροπία. Μπορούμε δηλαδή να διακρίνουμε τις εξής περιπτώσεις:

i) Αν Q_c = K_c το σύστημα βρίσκεται σε κατάσταση ισορροπίας
ii) Αν Q_c < K_c τότε η αντίδραση πηγαίνει προς τα δεξιά, ώστε η τιμή του Q_c να μεγαλώσει (μικραίνει ο παρανομαστής του κλάσματος και μεγαλώνει ο αριθμητής). Κατ΄ αυτό τον τρόπο το σύστημα προσεγγίζει τη θέση ισορροπίας, όπου Q_c = K_c.
iii) Αν Q_c > K_c, τότε η αντίδραση οδεύει προς τα αριστερά, ώστε το σύστημα να φτάσει σε ισορροπία.

• Q = Quotient (λόγος)

• Κατ΄ αντιστοιχία το Q_p είναι το πηλίκο των μερικών πιέσεων. Η σύγκριση του με το K_p αποτελεί τη βάση για τον καθορισμό της κατεύθυνσης μιας αντίδρασης.

Παράδειγμα 4.4

Σε δοχείο όγκου 10 L έχουμε σε ισορροπία 40 mol NH₃, 20 mol H₂ και 60 mol N₂. Ποια η τιμή της K_c των παρακάτω εξισώσεων που περιγράφουν το φαινόμενο:
Εικόνα

ΛΥΣΗ
Στην κατάσταση χημικής ισορροπίας οι συγκεντρώσεις των τριών σωμάτων είναι:

Εικόνα

Για την (1) η τιμή του κλάσματος Εικόνα στην ισορροπία ισούται με την K_c αυτής της εξίσωσης, άρα:

Εικόνα

Ανάλογα, για τη (2) η τιμή του κλάσματος Εικόνα στην ισορροπία ισούται με τη σταθερά ισορροπίας της εξίσωσης αυτής, K_c^' , οπότε:

Εικόνα

Εφαρμογή

Σε δοχείο όγκου V έχουμε σε ισορροπία ποσότητες SO₂, O₂ και SO₃. H K_c της αντίδρασης: 2 SO₂(g) + O₂ (g) ⇌ 2 SO₃(g) είναι 4 Lmol^-1.
Ποια είναι η τιμή της K_c για κάθε αντίδραση:
α. 2 SO₃ (g) ⇌ 2 SO₂ (g) + O₂(g)
β. SO₂ (g) + ½ O₂ ⇌ SO₃ (g)

• Οι μονάδες της K_c εξαρτώνται από τη μορφή της χημικής εξίσωσης. Συνήθως όμως αυτές παραλείπονται.

• Η τιμή της K_c δεν αναφέρεται στη χημική ισορροπία (δηλ. στο χημικό φαινόμενο) που πραγματοποιείται, αλλά στη χημική εξίσωση που περιγράφει την ισορροπία. Γι’ αυτό και η τιμή της αλλάζει, όταν αλλάξει ο τρόπος που γράφεται η χημική εξίσωση, ανεξάρτητα αν περιγράφεται πάντα η ίδια ισορροπία. Η Kc μιας ορισμένης χημικής εξίσωσης (με συγκεκριμένη φορά και συντελεστές) αλλάζει τιμή, μόνο αν αλλάξει η θερμοκρασία.

α. 0,25
β. 2

Παράδειγμα 4.5

Σε δοχείο όγκου 1 L υπάρχει ποσότητα στερεού C σε ισορροπία με 4 mol CO₂ και 8 mol CO. Ποια είναι η τιμή της K_c της χημικής εξίσωσης
CO₂(g) + C(s) ⇌ 2CO (g);

ΛΥΣΗ
Τα καθαρά στερεά σώματα παραλείπονται από την έκφραση της σταθεράς χημικής ισορροπίας. Η συγκέντρωση των στερεών θεωρείται σταθερή και η τιμή της είναι ενσωματωμένη στην τιμή της σταθεράς ισορροπίας. Έτσι, η σταθερά K_c της χημικής εξίσωσης
CO₂(g) + C(s) ⇌ 2CO (g)
είναι:

Εικόνα

Εφαρμογή

Σε δοχείο όγκου 1 L υπάρχει ποσότητα στερεού C σε ισορροπία με 2 mol CO₂ και 6 mol CO σε θερμοκρασία θ₁. Ποια είναι η τιμή του K_c για καθεμιά από τις παρακάτω των χημικές εξισώσεις:
α. CO₂(g) + C(s) ⇌ 2 CO(g)
β. 2 CO(g) ⇌ CO₂(g) + C(s)

Παράδειγμα 4.6

Σε δοχείο όγκου 1 L και σε θερμοκρασία 500 °C εισάγονται 3 mol H₂ και 3 mol I₂. Να υπολογίσετε τον αριθμό mol ΗΙ στη θέση ισορροπίας, καθώς και την απόδοση της αντίδρασης, αν η K_c της χημικής εξίσωσης

Η₂(g) + I₂(g) ⇌ 2HI(g) στους 500 °C ισούται με 49.

ΛΥΣΗ
Ονομάζουμε x mol την ποσότητα του Η₂ που αντιδρά και σχηματίζουμε τον παρακάτω πίνακα. Για το x υπάρχει ο περιορισμός: 0 < x < 3 ,
δηλαδή ως ποσότητα θα έχει θετική τιμή και μικρότερη από τα συνολικά mol Η₂ που διαθέτουμε.

ποσότητες / mol	Η₂(g) + I₂(g) ⇌ 2HI(g)
αρχικά	3	3	-
αντιδρούν	x	x	-
παράγονται	-	-	2x
ισορροπία	3 - x	3 - x	2x

α. 18
β. 1/18

Στην κατάσταση χημικής ισορροπίας ισχύει ο τύπος:

Εικόνα

λύση, η οποία ικανοποιεί τον περιορισμό που θέσαμε και είναι δεκτή.
Άρα στην ισορροπία θα έχουμε Εικόνα και η
απόδοση της αντίδρασης θα είναι

Εφαρμογή

Σε δοχείο όγκου 1 L και σε θερμοκρασία θ₁ εισάγονται 4 mol PCl₅ που διασπώνται μερικώς, σύμφωνα με τη χημική εξίσωση. Πόσα mol Cl₂ θα έχουμε στην ισορροπία αν η K_c της αντίδρασης:
PCl₅(g) ⇌ PCl₃(g) + Cl₂(g) ισούται με 9 σε θερμοκρασία θ₁.

Παράδειγμα 4.7

Σε δοχείο όγκου 41 L εισάγονται 2 mol N₂O₄. Θερμαίνουμε στους 27 °C οπότε το N₂O₄ διασπάται μερικώς, σύμφωνα με την αντίδραση:
N₂O₄(g) ⇌ 2NO₂(g)
Το αέριο μίγμα ισορροπίας έχει ολική πίεση P =1,8 atm. Ζητούνται:
α. Η συνολική ποσότητα σε mol (n_ολ) των ουσιών στη θέση ισορροπίας
β. Οι μερικές πιέσεις των αερίων στην ισορροπία
γ. Η τιμή της K_p της αντίδρασης.

ΛΥΣΗ
Ονομάζουμε x mol την ποσότητα του N₂O₄ που αντιδρά και σχηματίζουμε τον ακόλουθο πίνακα.

ποσότητες / mol	N₂O₄(g) ⇌ 2NO₂(g)
αρχικά	2	-
αντιδρούν	x
παράγονται		2x
ισορροπία	2-x	2x

Στην ισορροπία έχουμε:
n_oλ = (2-x+2x) mol = (2+x) mol
P = 1,8 atm
V = 41 L
T = θ +273 = 300 Κ
Γράφουμε την καταστατική εξίσωση για το μίγμα και έχουμε:

3 mol

Εικόνα

Εφαρμογή

Σε κλειστό δοχείο όγκου V = 8,2 L εισάγονται 2 mol PCl₅ και θερμαίνουμε στους 227 °C, οπότε ο PCl₅ διασπάται μερικώς σύμφωνα με την αντίδραση:
PCl₅(g) ⇌ PCl₃(g) + Cl₂(g)
Το αέριο μίγμα ισορροπίας έχει ολική πίεση P =12,5 atm.
(α) Ποιες είναι οι μερικές πιέσεις των τριών αερίων στην ισορροπία;
(β) Ποια είναι η τιμή της K_p της αντίδρασης;

Παράδειγμα 4.8

Σε δοχείο όγκου V = 20 L εισάγονται στους 500 °C 4 g Η₂, 508 g Ι₂ και 1024 g HI. Να διερευνήσετε αν το σύστημα είναι σε ισορροπία. Αν όχι, προς ποια κατεύθυνση οδεύει η αντίδραση και ποιες θα είναι οι ποσότητες των αερίων στη θέση ισορροπίας; Δίνεται ότι, η K_c της παρακάτω αντίδρασης στους 500 °C είναι 9.

Η₂(g) + Ι₂(g) ⇌ 2ΗΙ(g)

ΛΥΣΗ
Υπολογίζουμε τον αριθμό mol των τριών αερίων στην αρχική κατάσταση:
Εικόνα
Υπολογίζουμε την τιμή του κλάσματος:

στην αρχική κατάσταση, ώστε να διερευνήσουμε προς ποια κατεύθυνση οδεύει η αντίδραση:

p _Cl2 =2,5 atm, Κp = 5/6

Εικόνα

Διαπιστώνουμε ότι Q_c > K_c, συνεπώς το σύστημα δεν είναι σε κατάσταση ισορροπίας και μάλιστα η αντίδραση οδεύει προς τα αριστερά μέχρις ότου το κλάσμα πάρει την τιμή Q_c' = K_c. Ονομάζουμε x mol την ποσότητα του ΗΙ που αντιδρά και σχηματίζουμε το σχετικό πίνακα.

ποσότητες / mol	Η₂(g) + Ι₂(g) ⇌ 2ΗΙ(g)
αρχικά	2	2	8
αντιδρούν			x
παράγονται	x/2	x/2
ισορροπία	2 + x/2	2 + x/2	8-x

Στην ισορροπία:
Εικόνα
Η σύσταση του μίγματος στην ισορροπία είναι: 7,2 mol HI, 2,4 mol Η₂ και 2,4 mol Ι₂.

Εφαρμογή

Σε δοχείο όγκου 10 L, εισάγουμε 0,6 mol N₂, 0,4 mol Η₂ και 0,4 mol NH₃ σε θερμοκρασία 375 °C. Αν η K_c της αντίδρασης:
Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g)
στους 375 °C είναι ίση με 1,2, να διερευνήσετε αν το σύστημα είναι σε ισορροπία και αν όχι, προς ποια κατεύθυνση οδεύει η αντίδραση.

Παράδειγμα 4.9

Σε δοχείο όγκου 1 L που περιέχει σε ισορροπία 0,8 mol SO₂, 0,1 mol NO₂, 0,6 mol SO₃ και 0,4 mol NO προσθέτουμε 0,3 mol NO₂. Τι θα συμβεί στην ισορροπία και ποια θα είναι η ποσότητα του ΝΟ₂ στην τελική ισορροπία;
Δίνεται η ισορροπία: SO₂(g) + NO₂(g) ⇌ SO₃(g) + NO(g).

ΛΥΣΗ
Αφού στην ισορροπία προστέθηκε NO₂, η αντίδραση σύμφωνα με την αρχή Le Chatelier θα προχωρήσει προς τα δεξιά, οπότε η ποσότητα του NO₂ ελαττώνεται. Σχηματίζουμε τον παρακάτω πίνακα:

ποσότητες / mol	SO₂(g) + NO₂(g) ⇌ SO₃(g) + NO(g)
αρχική ισορροπία	0,8	0,1	0,6	0,4
προσθέτουμε	-	0,3	-	-
αντιδρούν	x	x	-	-
σχηματίζονται	-	-	x	x
τελική ισορροπία	0,8-x	0,4-x	0,6+x	0,4+x

Από την αρχική ισορροπία υπολογίζουμε την K_c: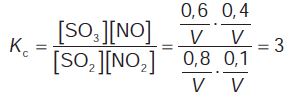

όπου V ο όγκος του δοχείου σε L.
Αφού η θ παραμένει σταθερή, η K_c δε μεταβάλλεται και στην τελική ισορροπία έχουμε:
Εικόνα
Η δεκτή λύση είναι x = 0,17, οπότε στην τελική ισορροπία έχουμε (0,4–0,17) mol = 0,23 mol NO₂.

Εφαρμογή

Σε δοχείο 2 L έχουμε σε ισορροπία 4 mol PCl₅, 2 mol PCl₃ και 8 mol Cl₂. Προσθέτουμε 4 mol PCl₅. Ποιες οι ποσότητες όλων των αερίων στη νέα ισορροπία;
Δίνεται η ισορροπία: PCl₅(g) ⇌ PCl₃(g) + Cl₂(g)

Παράδειγμα 4.10

Σε δοχείο όγκου 2 L έχουμε σε ισορροπία 8 mol PCl₅, 4 mol PCl₃ και 8 mol Cl₂. Διπλασιάζουμε τον όγκο του δοχείου και διατηρούμε τη θερμοκρασία σταθερή. Πόσα mol Cl₂ θα έχουμε στη νέα ισορροπία;
Δίνεται η εξίσωση ισορροπίας: PCl₅(g) ⇌ PCl₃(g) + Cl₂(g)

ΛΥΣΗ
Η αύξηση του όγκου του δοχείου ελαττώνει την πίεση του μίγματος.
Σύμφωνα με την αρχή Le Chatelier, η χημική ισορροπία μετατοπίζεται προς τα δεξιά, όπου υπάρχουν περισσότερα mol αερίων σωμάτων. Ονομάζουμε x mol την ποσότητα PCl₅(g) που αντιδρά και συμπληρώνουμε τον ακόλουθο πίνακα:

ποσότητες / mol	PCl₅(g) ⇌ PCl₃(g) + Cl₂(g)
αρχική ισορροπία	8	4	8
αντιδρούν	x	-	-
σχηματίζονται	-	x	x
τελική ισορροπία.	8-x	4+x	8+x

6,94 mol, 3,06 mol,
9,06 mol

Από την αρχική ισορροπία υπολογίζουμε την τιμή της K_c: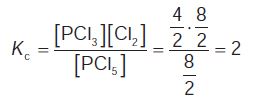

Η θερμοκρασία μένει σταθερή, άρα και η K_c. Στην τελική ισορροπία από την τιμή της Kc υπολογίζουμε: Εικόνα
ή χ=1,49 η μόνη δεκτή λύση που ικανοποιεί τον περιορισμό 0<x<8. Επομένως το Cl₂ στην τελική ισορροπία θα είναι: (8+1,49) mol = 9,49 mol.

Εφαρμογή

Σε ένα δοχείο που έχει όγκο V₁ = 3 L βρίσκονται σε ισορροπία 2 mol N₂O₄ και 1 mol NO₂, σύμφωνα με τη χημική εξίσωση:
N₂O₄(g) ⇌ 2NO₂(g)
α. Να βρείτε την τιμή της K_c
β. Διατηρώντας σταθερή τη θερμοκρασία, αυξάνουμε τον όγκο του δοχείου σε V₂ = 16 L. Τι θα συμβεί; Πόσα mol από κάθε αέριο θα υπάρχουν στο δοχείο, όταν αποκατασταθεί και πάλι η χημική ισορροπία;

Παράδειγμα 4.11

Σε δοχείο όγκου 10 L εισάγονται 1 mol Η₂ και 1 mol I₂ στους 450 °C.
Μετά την αποκατάσταση της χημικής ισορροπίας στους 450 °C, σύμφωνα με τη χημική εξίσωση: Η₂(g) + I₂(g) ⇌ 2HI(g)
η ποσότητα του Η₂ γίνεται 0,4 mol.
α. Ποια είναι η τιμή της K_c στους 450 °C;
β. Στη συνέχεια το μίγμα ισορροπίας θερμαίνεται στους 600 °C, στη νέα κατάσταση χημικής ισορροπίας, η ποσότητα του Η₂ γίνεται 0,2 mol. Να βρεθεί η τιμή της K_c στη νέα ισορροπία , στους 600 °C.
γ. Να βρεθεί αν η αντίδραση σχηματισμού του ΗΙ είναι ενδόθερμη ή εξώθερμη.

ΛΥΣΗ
α. Η ποσότητα του Η₂ που αντιδρά στους 450 °C είναι προφανώς (1–0,4) mol = 0,6 mol. Σχηματίζουμε το γνωστό πίνακα:

ποσότητες / mol	Η₂(g) + I₂(g) ⇌ 2HI(g)
αρχικά	1	1	-
αντιδρούν	0,6	0,6	-
σχηματίζονται	-	-	1,2
ισορροπία	0,4	0,4	1,2

1,5 mol N₂O₄, 2 mol NO₂

Στην κατάσταση χημικής ισορροπίας στους 450 °C: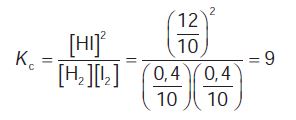

β. Με την αύξηση της θερμοκρασίας η ισορροπία μετατοπίζεται προς τα δεξιά, όπως φαίνεται από την εκφώνηση, και αντιδρούν (0,4–0,2) mol Η₂. Μετά από αυτή την παρατήρηση σχηματίζουμε πάλι τον αντίστοιχο πίνακα:

ποσότητες / mol	Η₂(g) + I₂(g) ⇌ 2HI(g)
αρχικά	0,4	0,4	1,2
αντιδρούν	0,2	0,2	-
σχηματίζονται	-	-	0,4
ισορροπία	0,2	0,2	1,6

Στην κατάσταση χημικής ισορροπίας στους 600 °C:
Εικόνα
γ. Παρατηρούμε ότι με αύξηση της θερμοκρασίας η αντίδραση σχηματισμού του ΗΙ μετατοπίζεται προς τα δεξιά, άρα σύμφωνα με την αρχή Le Chatelier η αντίδραση σχηματισμού του ΗΙ είναι ενδόθερμη.

Εφαρμογή

Σε δοχείο όγκου 3 L στους θ °C, ισορροπούν 5 mol Ν₂, 4 mol H₂ και 12 mol NH₃, σύμφωνα με την αντίδραση:
Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g).
Aν αυξηθεί η θερμοκρασία, το Ν₂ στη νέα ισορροπία βρίσκεται 5,5 mol.
α. Ποια είναι η σύσταση του μίγματος στη νέα ισορροπία;
β. Ποια η νέα τιμή της K_c;
γ. Η σύνθεση της NH₃ είναι εξώθερμη ή ενδόθερμη;

Γνωρίζεις ότι...
Το φαινόμενο του «θερμοκηπίου» και οι ωκεανοί
Κατά τη διάρκεια των επερχομένων δεκαετιών και αιώνων, το κλίμα της γης αναμένεται να αντιμετωπίσει μία μάλλον απρόσμενη αλλαγή που θα οφείλεται στις ανθρώπινες δραστηριότητες. Με κύρια αιτία την καύση των απολιθωμένων καυσίμων (πετρέλαιο, κάρβουνο), η συγκέντρωση του διοξειδίου του άνθρακα στην ατμόσφαιρα αυξάνει σταθερά. Το διοξείδιο του άνθρακα, ως γνωστό, απορροφά μέρος από τη θερμότητα που ανακλάται από την επιφάνεια της γης, προς το διάστημα. Έτσι, η αύξηση της συγκέντρωση του CO₂ στην ατμόσφαιρα ενισχύει το φαινόμενο του θερμοκηπίου, το οποίο ανυψώνει τη μέση θερμοκρασία της επιφάνειας της γης. Αυτό θα επιφέρει απρόσμενες αλλαγές στις κλιματολογικές ισορροπίες του πλανήτη μας. Ένας αριθμός ερευνητών προσπάθησε να προβλέψει το επίπεδο της αύξησης του CO₂ για τον επόμενο αιώνα. Οι προβλέψεις τους καλύπτουν ένα μεγάλο φάσμα πιθανοτήτων και υποθέσεων. Αυτό συμβαίνει γιατί αφενός μεν δεν μπορεί να γίνει ασφαλής πρόβλεψη της ποσότητας των καυσίμων που θα καταναλωθούν τα επόμενα 100 χρόνια, αφετέρου δεν μπορούμε με ακρίβεια να υπολογίσουμε τις ποσότητες του CO₂ που μπορούν να απορροφηθούν από τους ωκεανούς την ίδια περίοδο. Το τελευταίο αυτό θέμα, της απορρόφησης δηλαδή CO₂ από την θάλασσα, δεν είναι τίποτα άλλο παρά μία εφαρμογή της αρχής του Le Chatelier σε επίπεδο όμως υδρογείου σφαίρας. Το συμπέρασμα δε στο οποίο καταλήγουν οι επιστήμονες είναι ότι, το CO₂ θα έχει την ίδια δυσμενή επίδραση τόσο στην ατμόσφαιρα όσο και στους ωκεανούς. Ανάμεσα στις άλλες ισορροπίες που επικρατούν στους ωκεανούς, ιδιαίτερη σημασία έχουν εκείνες που καθορίζουν την	καταβύθιση ή αναδιάλυση του CaCO₃ το οποίο μεταξύ των άλλων αποτελεί βασικό συστατικό του κελύφους πολλών θαλασσίων οργανισμών όπως κοράλλια, στρείδια, κλπ. Αυτό βέβαια πέρα από το γεγονός ότι το CaCO₃ συνιστά βασικό συστατικό των ασβεστολιθικών αποθέσεων και βράχων πολλών θαλασσίων και υποθαλάσσιων περιοχών. Οι ισορροπίες αυτές, είναι: CaCO₃(s) ⇌ Ca²⁺ + CO₃^2- (1) και CO₃^2- + CO₂ + H₂O ⇌ HCO₃^- (2) Έτσι, καθώς αυξάνεται η συγκέντρωση του CO₂ η ισορροπία μετατοπίζεται προς τα δεξιά (αρχή του Le Chatelier), οπότε μειώνεται η συγκέντρωση των CO₃^2-. Τα τελευταία μετατοπίζουν την (1) προς τα δεξιά προκαλώντας αναδιάλυση των ασβεστολιθικών αποθέσεων. Αυτό θα έχει σοβαρότατες συνέπειες στα θαλάσσια οικοσυστήματα. Οι σχετικοί υπολογισμοί δείχνουν ότι αν ο θαλάσσιος βυθός αποτελείται μόνο από CaCO₃ και διαλυθεί από αυτόν ένα ύψος 3 cm, τότε στα επόμενα 1500 χρόνια θα μειωθεί η συγκέντρωση του CO₂ στην ατμόσφαιρα κατά 30% χωρίς μάλιστα να αλλάξει το pH της θάλασσας ( ~ 8,5). Βλέπει δηλαδή κανείς ότι η απορρόφηση του διοξειδίου του άνθρακα από τους ωκεανούς μπορεί να «λύνει» από την μία πλευρά το θέμα του θερμοκηπίου, από την άλλη όμως δημιουργεί ένα εξίσου μεγάλο πρόβλημα, όπως είναι η αναδιάλυση των ασβεστολιθικών αποθέσεων και των κελυφών των θαλασσίων οργανισμών. Μία τέτοια μαζική εξαφάνιση τέτοιων οργανισμών από τις ακτές και τους υποθαλάσσιους χώρους έχει ίσως μεγαλύτερη σημασία από την τυχόν αύξηση του CO₂ στην ατμόσφαιρα και πρέπει με ιδιαίτερη προσοχή να μελετηθεί και ν' αντιμετωπιστεί.

Ανακεφαλαίωση
1.	Η κατάσταση χημικής ισορροπίας είναι μια δυναμική ισορροπία κατά την οποία οι ταχύτητες των δύο αντιθέτων αντιδράσεων εξισώνονται.
2.	Αντιδράσεις που καταλήγουν σε κατάσταση χημικής ισορροπίας ονομάζονται αμφίδρομες αντιδράσεις.
3.	Όταν τα αντιδρώντα και προϊόντα σε μια χημική ισορροπία είναι στην ίδια φάση η ισορροπία ονομάζεται ομογενής, σε αντίθετη περίπτωση ονομάζεται ετερογενής.
4.	Απόδοση μιας αντίδρασης είναι ο λόγος της ποσότητας ενός προϊόντος που σχηματίζεται πρακτικά, προς την ποσότητα που θα σχηματιζόταν αν η αντίδραση ήταν μονόδρομη.
5.	Οι παράγοντες που επηρεάζουν τη θέση χημικής ισορροπίας είναι: α. η συγκέντρωση των αντιδρώντων ή προϊόντων, β. η πίεση και γ. η θερμοκρασία.
6.	Αρχή Le Chatelier: Όταν μεταβάλλουμε ένα από τους συντελεστές ισορροπίας η θέση της ισορροπίας μετατοπίζεται προς την κατεύθυνση που τείνει να αναιρέσει τη μεταβολή που επιφέραμε.
7.	Αύξηση της θερμοκρασίας ευνοεί την ενδόθερμη αντίδραση. Αύξηση της πίεσης, η οποία συντελείται με ελάττωση όγκου, μετατοπίζει την ισορροπία προς την κατεύθυνση που ελαττώνεται ο αριθμός των mol των αερίων. Αύξηση της συγκέντρωσης μιας ουσίας που μετέχει στην ισορροπία μετατοπίζει την ισορροπία προς την κατεύθυνση που καταναλίσκεται η ουσία αυτή.
8.	Κριτήριο για την κατεύθυνση προς την οποία θα γίνει η αντίδραση είναι η σχέση Q_c με K_c. Aν Q_c = K_c τότε η αντίδραση είναι σε κατάσταση χημικής ισορροπίας. Αν Q_c < K_c τότε η αντίδραση οδεύει προς τα δεξιά. Αν Q_c > K_c τότε η αντίδραση οδεύει προς τα αριστερά.
9.	Η σχέση που συνδέει το K_c με το K_p είναι : K_p = K_c^.(RT)^Δn.

Λέξεις Κλειδιά

Χημική Ισορροπία	Απόδοση αντίδρασης
Αμφίδρομη αντίδραση	Αρχή Le Chatelier
Ομογενής ισορροπία	Σταθερά χημικής ισορροπίας
Ετερογενής ισορροπία

Ερωτήσεις – Ασκήσεις - Προβλήματα
Ερωτήσεις Επανάληψης
1.	Tι σημαίνει ότι η χημική ισορροπία είναι δυναμική ισορροπία;
2.	Ποιες αντιδράσεις ονομάζονται αμφίδρομες;
3.	Τι ονομάζεται ομογενής ισορροπία και τι ετερογενής; Δώστε ένα παράδειγμα για κάθε περίπτωση.
4.	Τι είναι απόδοση αμφίδρομης αντίδρασης;
5.	Ποιοι παράγοντες επηρεάζουν τη θέση χημικής ισορροπίας;
6.	Τι λέει η αρχή Le Chatelier;
7.	Προς τα πού θα μετατοπιστεί η ισορροπία στην αμφίδρομη αντίδραση CO(g) + 2H₂(g) ⇌ CH₃OH(g) ΔΗ < 0 α. αν αυξήσουμε τη θερμοκρασία; β. αν ελαττώσουμε τον όγκο του δοχείου που περιέχει τα αέρια ισορροπίας σε σταθερή θερμοκρασία; γ. Αν προσθέσουμε στο μίγμα ισορροπίας H₂;
8.	Με τι μονάδες μετράμε την K_c και την K_p της χημικής εξίσωσης: Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g);
9.	Ποια σχέση συνδέει την K_c, την K_p και την απόλυτη θερμοκρασία T στην προηγούμενη χημική εξίσωση;

Ασκήσεις - Προβλήματα
α. Χημική Ισορροπία - Απόδοση
10.	Ποιες από τις παρακάτω ισορροπίες είναι ομογενείς και ποιες ετερογενείς; α. Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g) β. CaCO₃(s) ⇌ CaO(s) + CO₂(g) γ. AgCl(s) ⇌ Ag⁺(aq) + Cl^-(aq) δ. NH₄⁺(aq) + F^-(aq) ⇌ NH₃(aq) + HF(aq)
11.	Να συμπληρώσετε τα κενά στις επόμενες προτάσεις: α. Στην κατάσταση χημικής ισορροπίας συνυπάρχουν ποσότητες από όλα τα ……………… και …………………, χωρίς οι ποσότητές τους να …………………… με την πάροδο του χρόνου, εφόσον οι συνθήκες παραμένουν σταθερές. β. Η χημική ισορροπία είναι ………………….. και όχι στατική. Αυτό σημαίνει ότι οι αντιδράσεις πραγματοποιούνται ταυτόχρονα και με την …………… ταχύτητα.

	γ. Αντιδράσεις που πραγματοποιούνται και προς τις δύο κατευθύνσεις ταυτόχρονα και καταλήγουν σε κατάσταση …………………. ονομάζονται …………………… αντιδράσεις. δ. Ομογενή ισορροπία έχουμε όταν τα αντιδρώντα και …………………......... βρίσκονται σε ……………… φάση. Ετερογενή ισορροπία έχουμε όταν τα …………………… και τα προϊόντα βρίσκονται ………………………………. από μία φάσεις.
12.	Ποια από τις παρακάτω προτάσεις που αφορούν τη χημική ισορροπία είναι λάθος; α. Στην κατάσταση ισορροπίας οι ταχύτητες των δύο αντιδράσεων που εκφράζουν τις δύο αντίθετες φορές είναι ίσες. β. Στην κατάσταση ισορροπίας οι ποσότητες όλων των σωμάτων που είναι παρόντα, είναι ίσες. γ. Η κατάσταση χημικής ισορροπίας είναι μια δυναμική ισορροπία.
13.	Δίνεται η ισορροπία: 2A(g) + B(g) ⇌ Γ(g). Προσθέτουμε σε κενό δοχείο ίσο αριθμό mol Β και Γ και καθόλου A. Στην ισορροπία θα έχουμε οπωσδήποτε: α. [Α] = [Β] β. [Β] = [Γ] γ. [Α] < [Γ] δ. [Β] > [Γ]
14.	Δίνεται η ισορροπία: Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g). Σε δοχείο προσθέτουμε ίσο αριθμό mol Ν₂ και H₂. Στην ισορροπία, ποια από τις παρακάτω σχέσεις είναι οπωσδήποτε σωστή; α. [H₂] > [NH₃] β. [Ν₂] > [H₂] γ. [H₂] > [Ν₂] δ. [NH₃] > [Ν₂]
15.	Να συμπληρώσετε με ένα Σ όσες από τις επόμενες προτάσεις είναι σωστές και με Λ όσες είναι λανθασμένες. α. Οι μονόδρομες αντιδράσεις έχουν πάντοτε μεγάλη ταχύτητα και οι αμφίδρομες έχουν πάντοτε μικρή ταχύτητα. β. Η απόδοση μιας αμφίδρομης αντίδρασης είναι πάντοτε μικρότερη του 1. γ. Στην κατάσταση χημικής ισορροπίας οι συγκεντρώσεις όλων των αντιδρώντων είναι πάντοτε ίσες μεταξύ τους. δ. Στην κατάσταση χημικής ισορροπίας εφόσον οι συνθήκες παραμένουν σταθερές, οι συγκεντρώσεις όλων των αντιδρώντων και προϊόντων παραμένουν σταθερές.
16.	Σε κλειστό δοχείο σταθερού όγκου 2 L εισάγουμε 4 mol PCl₅ και θερμαίνουμε στους 200 °C οπότε αποκαθίσταται η ισορροπία PCl₅(g) ⇌ PCl₃(g) + Cl₂(g) Αν η απόδοση είναι α = 60%, να βρείτε: α. τις ποσότητες των τριών αερίων στην ισορροπία β. τις συγκεντρώσεις των τριών αερίων στην ισορροπία	α. 2,4 mol Cl₂ β. c_Cl₂=1,2 M
*17.	Σε κλειστό δοχείο σταθερού όγκου V = 41 L εισάγουμε 29,7 g φωσγενίου COCl₂ και θερμαίνουμε στους 227 °C, οπότε αποκαθίσταται η ισορροπία:
	Χημική ισορροπία

	COCl₂(g) ⇌ CO(g) + Cl₂(g) στην κατάσταση χημικής ισορροπίας έχουμε 4,2 g CO. Ζητούνται: α. οι ποσότητες των τριών αερίων στην ισορροπία. β. η απόδοση της αντίδρασης γ. η πίεση κάθε αερίου στην ισορροπία δ. η ολική πίεση του μίγματος των τριών αερίων στην ισορροπία.	α. 0,15 mol COCl₂ β. 50% γ. p_Cl₂=0,15 atm δ. Ρ = 0,45 atm
*18.	Σε κλειστό δοχείο σταθερού όγκου V = 0,82 L εισάγουμε 0,04 mol N₂O₄ και θερμαίνουμε στους 127 °C, οπότε αποκαθίσταται η ισορροπία: N₂O₄(g) ⇌ 2NO₂(g) Σε σταθερή θερμοκρασία (θ = 127 °C) και στην ισορροπία η ολική πίεση είναι 2 atm. α. Πόσα mol από κάθε αερίο υπάρχουν στην ισορροπία; β. Ποια η μερική πίεση κάθε αερίου στην ισορροπία; γ. Ποιος είναι ο βαθμός διάσπασης του N₂O₄, ποια είναι δηλαδή η απόδοση της αντίδρασης;	α. 0,02 mol NO₂ β. p_NO₂=0,8 atm γ. 25%
*19.	Σε κλειστό δοχείο εισάγουμε ποσότητα CO₂ και θερμαίνουμε στους 1127 °C, οπότε διασπάται το CO₂ κατά 50% σύμφωνα με την αντίδραση: 2CO₂(g) ⇌ 2CO(g) + O₂(g) Στην ισορροπία, ποια από τις ακόλουθες σχέσεις ισχύει; α. p_CO₂ = p_CO = p_O₂ γ. p_CO₂ = p_CO = 2p_O₂ β. p_O₂ = 2p_CO = p_CO₂ δ. p_CO₂ = 2p_CO = 2p_O₂

β. Παράγοντες που επηρεάζουν τη θέση χημικής ισορροπίας – Αρχή Le Chatelier
20.	Να συμπληρώσετε τα κενά στις προτάσεις: α. Όταν μεταβάλλουμε ένα από τους ………………….. ισορροπίας (συγκέντρωση, πίεση, θερμοκρασία) η θέση της ισορροπίας μετατοπίζεται προς εκείνη την κατεύθυνση που τείνει να ………………… τη μεταβολή που επιφέραμε. β. Μείωση της θερμοκρασίας μετατοπίζει την ισορροπία προς την κατεύθυνση εκείνη που ……………………. θερμότητα, δηλαδή ΔΗ είναι ……………… του μηδενός. γ. Μεταβολή της πίεσης που γίνεται με μεταβολή του ……………... του δοχείου επηρεάζει τη θέση ισορροπίας υπό την προϋπόθεση α. να μετέχουν στην ισορροπία ………….. σώματα και β. να παρατηρείται …………………. του αριθμού των mol των …………….. . Αύξηση της πίεσης (σε σταθερή θερμοκρασία) μετατοπίζει την ισορροπία προς την κατεύθυνση που προκαλεί …………….. του αριθμού των mol των αερίων.
21.	Δίνεται η ισορροπία COCl₂(g) ⇌ CO(g) + Cl₂(g) ΔΗ < 0. Προς τα πού θα μετατοπιστεί η ισορροπία αν:

	α. Αυξήσουμε τη θερμοκρασία β. Αυξήσουμε την πίεση ελαττώνοντας τον όγκο του δοχείου. γ. Προσθέσουμε στο δοχείο CO.
22.	Να σημειώσετε με Σ τις σωστές από τις επόμενες προτάσεις και με Λ τις λανθασμένες. α. H ισορροπία Η₂(g) + I₂(g) ⇌ 2ΗΙ(g) δεν επηρεάζεται αν αυξήσουμε τον όγκο του δοχείου σε σταθερή θερμοκρασία. β. Όταν αυξάνουμε τη θερμοκρασία αυξάνει η απόδοση μιας εξώθερμης αντίδρασης. γ. Προσθήκη καταλύτη αυξάνει την απόδοση της εξώθερμης αντίδρασης.
23.	Δίνονται οι ισορροπίες που περιγράφονται από τις αντιδράσεις: α. Η₂(g) + Ι₂(g) ⇌ 2ΗΙ(g) β. PCl₅(g) ⇌ PCl₃(g) + Cl₂(g) γ. CO₂(g) + C(s) ⇌ 2CO(g) δ. CaCO₃(s) ⇌ CaO(s) + CO₂(g) Σε ποιες από αυτές τις ισορροπίες όταν αυξάνουμε τον όγκο του δοχείου διαταράσσεται η ισορροπία και προς ποια κατεύθυνση οδεύει η αντίδραση ώστε να αναιρεθεί η μεταβολή;
24.	Δίνεται η ισορροπία 2SO₂ + O₂ ⇌2 SO₃ ΔΗ = -45 kcal. Ποια από τις επόμενες μεταβολές σε ένα μίγμα ισορροπίας SO₂, O₂ και SO₃ θα προκαλέσει αύξηση της ποσότητας του SO₃; α. Αύξηση της θερμοκρασίας. β. Ελάττωση του όγκου του δοχείου σε Τ = σταθερή. γ. Αφαίρεση ποσότητας O₂ από το δοχείο (V και Τ σταθερά). δ. Προσθήκη αδρανούς αερίου, π.χ. He ( με V και Τ σταθερά).
25.	Ποιες από τις ακόλουθες ισορροπίες δε θα διαταραχθούν αν αυξήσουμε τον όγκο του δοχείου σε σταθερή θερμοκρασία; α. Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g) β. Η₂(g) + Ι₂(g) ⇌ 2ΗΙ(g) γ. CO₂(g) + C(s) ⇌ 2CO(g) δ. C(s) + O₂(g) ⇌ CO₂(g) ε. 2ΝΟ(g) + O₂(g) ⇌2NO₂(g)
26.	Για την εξώθερμη αντίδραση: CO(g) + 2H₂(g) ⇌ CH₃OH(g) ΔΗ<0 α. πώς η αύξηση της θερμοκρασίας επηρεάζει την ταχύτητα και πώς την απόδοση της αντίδρασης; β. πώς η αύξηση της πίεσης επηρεάζει την ταχύτητα και πώς την απόδοση της αντίδρασης;
	Χημική ισορροπία

γ. Κc-Kp
27.	Δίνεται η ισορροπία: 2A(g) + B(g) ⇌ 2Γ(g). H σωστή έκφραση για την K_c είναι:
28.	Δίνεται η ισορροπία: Α(g) + 2B(g) ⇌ 2Γ(s) + Δ(g). H σωστή έκφραση για την K_c είναι:
29.	Σε δοχείο όγκου 2 L βρίσκονται σε ισορροπία 0,8 mol SO₂, 0,2 mol O₂ και 1,4 mol SO₃. Να βρεθεί η τιμή της K_c της χημικής εξίσωσης: 2SO₂(g) + O₂(g) ⇌2 SO₃(g).	30,625
30.	Σε δοχείο όγκου 0,5 L βρίσκονται σε ισορροπία 1 mol A, 2 mol B, και 3 mol Γ. Ποια είναι η τιμή της K_c της χημικής εξίσωσης A(g) + B(g) ⇌ 2Γ(g);	4,5
31.	Η K_c της αντίδρασης Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g) στους 360 °C είναι K_c =1,25. Ποια είναι η K_c της 2NH₃(g) ⇌ Ν₂(g) + 3H₂(g) στους 360 °C.	0,8
32.	Σε δοχείο βρίσκονται σε ισορροπία 5 mol NO₂, 2 mol NO και 5 mol O₂. Αν η K_c της αντίδρασης: 2NO₂(g) ⇌ 2ΝΟ(g) + O₂(g) είναι 0,2 mol/L, να βρεθεί ο όγκος του δοχείου.	4 L
33.	Δίνεται η ισορροπία: N₂O₄(g) ⇌ 2NO₂(g) ΔΗ > 0 (ενδόθερμη). Ποιες από τις παρακάτω μεταβολές θα ελαττώσουν την τιμή της K_c: α. Προσθήκη ποσότητας Ν₂Ο₄ β. Ελάττωση της θερμοκρασίας γ. Προσθήκη καταλύτη δ. Διπλασιασμός του όγκου του δοχείου.
34.	Σε δοχείο όγκου 2 L βάζουμε 4 mol Ν₂ και 10 mol H₂. Στην ισορροπία έχουμε 6 mol NH₃. Ποια είναι η απόδοση και ποια είναι η τιμή της σταθεράς χημικής ισορροπίας της χημικής εξίσωσης: Ν₂(g) + 3H₂(g) ⇌ 2NH₃(g);	90%, K_c=144
35.	Σε δοχείο όγκου 1 L βάζουμε 1 mol Η₂ και 1 mol Ι₂ και θερμαίνουμε σε θερμοκρασία θ. Πόσα mol HI θα σχηματιστούν, αν στη θερμοκρασία αυτή η K_c της χημικής εξίσωσης Η₂(g) + Ι₂(g) ⇌ 2ΗΙ(g) ισούται με 49;	14/9

*36.	Στους 200 °C η K_c της αντίδρασης: PCl₅(g) ⇌ PCl₃(g) + Cl₂(g) ΔΗ°=+124 kJ έχει την αριθμητική τιμή 8^.10^-3. α. Να γράψετε την έκφραση της K_c για την αντίδραση. β. Ποιες είναι οι μονάδες της K_c; γ. Ποια είναι η αριθμητική τιμή και οι μονάδες της K_c της αντίστροφης αντίδρασης: PCl₃(g) + Cl₂(g) ⇌ PCl₅(g) στους 200 °C; δ. Πώς θα μεταβληθούν οι ποσότητες των τριών αερίων στην ισορροπία: i. Αν προσθέσουμε νέα ποσότητα PCl₅; ii. Αν αυξηθεί η πίεση με ελάττωση του όγκου σε σταθερή θερμοκρασία; iii. Αν αυξηθεί η θερμοκρασία; iv. Πώς μεταβάλλεται η K_c σε κάθε μία από τις προηγούμενες μεταβολές;
37.	Όταν διαλύουμε φρουκτόζη (οπωροσάκχαρο) ή γλυκόζη (σταφυλοσάκχαρο) στο νερό αποκαθίσταται η ισορροπία: φρουκτόζη(aq) ⇌ γλυκόζη(aq) (1) Ένας χημικός παρασκεύασε στους 25 °C ένα διάλυμα φρουκτόζης 0,25 Μ. Στην ισορροπία βρέθηκε ότι η συγκέντρωση της φρουκτόζης ελαττώθηκε σε 0,15 Μ. α. Να βρείτε την K_c της (1). β. Πόσο % της φρουκτόζης μετατράπηκε σε γλυκόζη;	α. 0,67, β. 40%
38.	Η K_c της χημικής εξίσωσης CO(g) + H₂O(g) ⇌ CO₂(g) + H₂(g) στους 300 °C ισούται με 4. α. Σε κενό δοχείο βάζουμε 1 mol CO και 1 mol H₂O, στους 300 °C. Πόσα mol H₂ θα σχηματιστούν και ποια είναι η απόδοση της αντίδρασης; β. Αν βάζαμε 1 mol CO και 1,6 mol H₂O στους 300 °C, πόσα mol Η₂ θα σχηματίζονταν και ποια είναι η απόδοση;	α. 2/3, 66,67% β. 0,8, 80%
*39.	Σε κλειστό δοχείο και σε ορισμένη θερμοκρασία εισάγουμε 1 mol CO και 1 mol H₂O. Μετά την αποκατάσταση της ισορροπίας CO(g) + H₂O(g) ⇌ CO₂(g) + H₂(g) (1) παραμένει χωρίς να αντιδράσει 1/3 mol CO. α. Να υπολογίσετε τη σταθερά ισορροπίας, K_c, της (1). β. Πόσα επιπλέον mol υδρατμών πρέπει να προστεθούν στο αρχικό μίγμα και στην ίδια θερμοκρασία, ώστε η απόδοση της αντίδρασης να γίνει 80%;	α. K_c = 4, β. 0,6 mol Δύο λύσεις: 3,2 mol ή 1,25 mol
40.	Η K_c της Α(g) + B(g) ⇌ Γ(g) + Δ(g) ισούται με 4. Σε κενό δοχείο βάζουμε 2 mol A. Πόσα mol από το Β πρέπει να βάλουμε για να αντιδράσουν τα σώματα με απόδοση 80%;
*41.	Σε κενό δοχείο όγκου V και σε θερμοκρασία θ εισάγουμε 1 mol αερίου Α και 1 mol αερίου Β, οπότε γίνεται η αντίδραση: A(g) + B(g) ⇌ Γ(g) με απόδοση 60%. Σε άλλο κενό δοχείο όγκου V και σε θερμοκρασία θ εισάγουμε 1 mol του Α και 2 mol του Β. Η νέα απόδοση της αντίδρασης θα είναι:
	Χημική ισορροπία

	α. 60% β. μεγαλύτερη από 60% γ. μικρότερη από 60% δ. εξαρτάται.
42.	Σε δοχείο όγκου 1 L που περιέχει σε ισορροπία 0,8 mol SO₂, 0,1 mol NO₂, 0,6 mol SO₃ και 0,4 mol NO προσθέτουμε 0,3 mol NO₂. Τι θα συμβεί και ποια θα είναι η ποσότητα του NO₂ στην τελική ισορροπία; Δίνεται η ισορροπία: SO₂(g) + NO₂(g) ⇌ SO₃(g) + NO(g).	0,23 mol NO₂
43.	Σε δοχείο 2 L έχουμε σε ισορροπία 4 mol PCl₅, 2 mol PCl₃ και 8 mol Cl₂. Προσθέτουμε 4 mol PCl₅. Ποιες οι ποσότητες όλων των αερίων στη νέα ισορροπία; Δίνεται η ισορροπία: PCl₅(g) ⇌ PCl₃(g) + Cl₂(g)	6,94 mol PCl₅
44.	Σε δοχείο έχουμε σε ισορροπία 2 mol SO₂, 4 mol NO₂, 8 mol SO₃ και 3 mol NO. α. Ποια είναι η K_c της χημικής εξίσωσης SO₂(g) + NO₂(g) ⇌ SO₃(g) + NO(g) στην παραπάνω θερμοκρασία; β. Πόσα mol SO₂ πρέπει να προσθέσουμε στην αρχική ισορροπία και σε σταθερή θερμοκρασία, ώστε η ποσότητα του NO να αυξηθεί κατά 1 mol;	β. 3 mol
45.	Σε κενό δοχείο σταθερού όγκου 4,1 L βάζουμε 46 g N₂O₄ και θερμαίνουμε στους 27 °C, οπότε το N₂O₄ διασπάται μερικώς σύμφωνα με την αντίδραση: N₂O₄(g) ⇌ 2NO₂(g). Πόσα mol NO₂ θα σχηματιστούν αν η θερμοκρασία είναι σταθερή και η K_p της αντίδρασης είναι ίση με 2 atm; Δίνεται η παγκόσμια σταθερά των αερίων R=0,082 L^.atm/mol^.K.	1/3 mol NO2
46.	Σε κλειστό δοχείο που έχει όγκο 0,224 L βάζουμε 0,01 mol COCl₂ και θερμαίνουμε στους 273 °C, οπότε το COCl₂ διασπάται μερικώς σε CO και Cl₂, και η τελική πίεση γίνεται 3,5 atm. Ποια είναι η απόδοση της αντίδρασης και ποια η τιμή της K_p της χημικής εξίσωσης: COCl₂(g) ⇌ CO(g) + Cl₂(g), στους 273 °C;	75%, Kp=4,5
47.	Στους 817 °C η αντίδραση CO₂ με περίσσεια στερεού C γίνεται με απόδοση 62%. Η ολική πίεση στην κατάσταση ισορροπίας είναι 3,24 atm. Ποια είναι η μερική πίεση κάθε αερίου στην κατάσταση χημικής ισορροπίας και ποια είναι η K_p της χημικής εξίσωσης CO₂(g) + C(s) ⇌ 2CO(g);	P_CO=2,48 atm K_p=8,09 atm
48.	Δοχείο περιέχει 0,8 mol SO₂, 0,1 mol NO₂, 0,6 mol SO₃ και 0,4 mol NO σε ισορροπία: SO₂(g) + NO₂(g) ⇌ SO₃(g) + NO(g). Πόσα mol NO πρέπει να εισαχθούν στο δοχείο στην ίδια θερμοκρασία, ώστε να μπορεί να αυξηθεί η ποσότητα του NO₂ κατά 0,2 mol;	2,05 mol
*49.	Σε δοχείο όγκου 2 L στους 1800 °C περιέχονται σε χημική ισορροπία 0,3 mol CO₂, 0,3 mol H₂, 0,6 mol CO και 0,6 mol H₂O. α. Να βρεθεί η K_c της εξίσωσης

	CO₂(g) + H₂(g) ⇌ CO(g) + H₂O(g) στους 1800 °C. β. Πόσα mol CO₂ πρέπει να προσθέσουμε στην αρχική ισορροπία, ώστε η συγκέντρωση του CO να γίνει 0,35 Μ;	α. 4, β. 0,4125 mol
*50.	Σε δοχείο όγκου 2 L περιέχονται σε ισορροπία 4 mol SO₃, 4 mol SO₂ και 0,5 mol O₂ στους 227 °C σύμφωνα με τη χημική εξίσωση: 2SO₃(g) ⇌ 2SO₂(g) + O₂(g) Θερμαίνουμε το μίγμα στους 427 °C, οπότε μετά την αποκατάσταση της νέας ισορροπίας διαπιστώσαμε ότι περιέχονται στο δοχείο συνολικά 9 mol αερίων. α. Να υπολογίσετε τη σταθερά K_c στους 227 °C. β. Να υπολογίσετε τη σταθερά K_c στους 427 °C. γ. Να εξηγήσετε αν η αντίδραση 2SO₃(g) ⇌ 2SO₂(g) + O₂(g) είναι εξώθερμη ή ενδόθερμη.	α. ¼ , β. 25/18, γ. ενδόθερμη

Γενικά Προβλήματα
*51.	Δίνεται η ισορροπία: 2NO(g) + Cl₂(g) ⇌ 2NOCl(g). Σε δοχείο όγκου 25 L προσθέτουμε 0,3 mol NO, 0,2 mol Cl₂ και 0,5 mol NOCl. Στην ισορροπία έχουμε τελικά 0,6 mol NOCl. i. Ο αριθμός των mol του Cl₂ στην ισορροπία είναι: α. 0,2, β. 0,1, γ. 0,15, δ. 0,25. ii. Αν αυξηθεί ο όγκος του δοχείου στα 50 L: α. Θα αυξηθεί ο αριθμός των mol του ΝOCl; β. Θα αυξηθεί ο αριθμός των mol του Cl₂; γ. Δεν θα μεταβληθεί η ποσότητα του NOCl; iii. H τιμή της K_c είναι: α. 1,5^.10³, ή β. 2,5^.10³, ή γ. 2^.10^-1 δ. 9^.10²
**52.	Σε κενό δοχείο όγκου 10 L εισάγονται 0,5 mol Η₂ και 0,5 mol Ι₂, τα οποία θερμαίνονται στους 448 °C. Στη θερμοκρασία αυτή, για τη χημική αντίδραση Η₂(g) + Ι₂(g) ⇌ 2ΗΙ(g) η σταθερά της χημικής ισορροπίας K_c είναι 64. Να υπολογίσετε: α. τη σταθερά της χημικής ισορροπίας της αντίδρασης τη σχετική με τις μερικές πιέσεις (K_p) στην ίδια θερμοκρασία (448 °C). β. τη σύσταση του μίγματος στους 448 °C μετά την αποκατάσταση της χημικής ισορροπίας. γ. την ολική πίεση που ασκείται στο δοχείο, όταν η θερμοκρασία ανέλθει στους 727 °C. Δίνεται η παγκόσμια σταθερά των αερίων R=0,082 L^.atm/mol^.K.	K_p = 64, β. 0,8 mol HI, γ. 8,2 atm
**52.	Σήμερα το υδρογόνο παρασκευάζεται από το φυσικό αέριο με την ακόλουθη ενδόθερμη αντίδραση: CH₄(g) + H₂O(g) ⇌ CO(g) + 3H₂(g) (1) ΔH > 0. i. Να γράψετε την έκφραση της K_p για την αντίδραση (1) ii. Πώς μεταβάλλεται η K_p της (1); α. Με αύξηση της πίεσης
	Χημική ισορροπία

	β. Με αύξηση της θερμοκρασίας γ. Με χρήση καταλύτη iii. Αν σε μίγμα ισορροπίας των τεσσάρων αερίων κάνουμε τις εξής επεμβάσεις τι θα συμβεί; α. Αυξάνουμε την πίεση με ελάττωση όγκου. β. Αυξάνουμε τη θερμοκρασία. γ. Χρησιμοποιούμε καταλύτη.
**54.	Στους 817 °C η αναγωγή του CO₂ σε CO με περίσσεια γραφίτη έχει K_p=10 atm. α. Αν βάλουμε αρχικά x mol CO₂ και η ολική πίεση στην ισορροπία είναι 4 atm, ποια είναι η περιεκτικότητα σε mol του τελικού αερίου μίγματος; β. Ποια πρέπει να είναι η τιμή της ολικής πίεσης για να περιέχει το τελικό μίγμα 6% σε mol CO₂; Δίνεται: CO₂(g) + C(s) ⇌ 2CO(g).	α. 23,46% CO₂, β. 0,68 atm
**55.	Σε κενό δοχείο όγκου 41 L εισάγουμε 6 mol CaCO₃ και θερμαίνουμε στους 1227 °C, οπότε το CaCO₃ διασπάται όπως δείχνει η αντίδραση: CaCO₃(s) ⇌ CaO(s) + CO₂(g) Η K_p αυτής της αντίδρασης στους 1227 °C είναι ίση με 9 atm. α. Πόσα mol CaCO₃ θα διασπαστούν; β. Αν σε άλλο δοχείο όγκου 123 L εισάγουμε 6 mol CaCO₃ και θερμάνουμε στους 1227 °C τι θα συμβεί; γ. Ποιος είναι ο ελάχιστος όγκος για το δοχείο, ώστε όταν θερμάνουμε 6 mol CaCO₃ στους 1227 °C να διασπαστούν όλα; (Θεωρούμε ότι ο όγκος των στερεών είναι αμελητέος σε σχέση με τον όγκο του δοχείου, R=0,082 atm^.L/mol^.K)	α. 3 mol β. Θα διασπαστούν όλα γ. 82 L
**56.	Για την αντίδραση Η₂(g) + I₂(g) ⇌ 2HI(g) στους 450 °C η σταθερά χημικής ισορροπίας έχει τιμή 49. Στη θερμοκρασία αυτή ένα δοχείο περιέχει 0,2 mol Η₂, 0,2 mol I₂ και 0,5 mol HI. α. Να δείξετε ότι το σύστημα δε βρίσκεται σε ισορροπία. β. Εάν το σύστημα αφεθεί να ισορροπήσει, πόσα mol HI θα υπάρχουν στην ισορροπία; γ. Πόσα επιπλέον mol HI πρέπει να εισαχθούν στο δοχείο στην ισορροπία, έτσι ώστε η ποσότητα του Η₂ να ξαναγίνει 0,2 mol;	β. 0,7 mol, γ. 0,9 mol
**57.	Ένα μίγμα σε ισορροπία περιέχει 0,52 mol N₂O₄ και 0,96 mol NO₂ στους 100 °C. Το μίγμα των δύο αερίων μεταφέρεται σε ένα άλλο δοχείο με διπλάσιο όγκο αλλά στην ίδια θερμοκρασία. Πόσα mol κάθε ουσίας θα περιέχονται στο νέο δοχείο στην ισορροπία;	0,4 mol N₂O₄, 1,2 mol NO₂
**58.	Δίνεται η απλή αντίδραση (χωρίς ενδιάμεσα στάδια): 2ΝΟ(g) + O₂(g) ⇌ 2NO₂(g) όπου k₁ = 2,6^.10³ L²mol^-2s^-1 (σταθερά ταχύτητας της προς τα δεξιά αντίδρασης) και k₂ = 4 L²mol^-2s^-1 (αντίστοιχα προς τα αριστερά) στους λ °C. α. Ποια η K_c στους λ °C; β. Ποια η αρχική ταχύτητα παρασκευής NO₂, αν οι αρχικές συγκεντρώσεις των ΝΟ και O₂ είναι 6^.10^-3 mol/L και 0,3 mol/L αντίστοιχα;

	Σε θερμοκρασία μ °C (μ<λ) σε δοχείο όγκου 5 L βάζουμε 0,2 mol NO₂. Όταν αποκατασταθεί η χημική ισορροπία, έχει διασπαστεί το 15% της αρχικής ποσότητας του NO₂. γ. Ποια η K_c' στους μ °C της 2ΝΟ(g) + O₂(g) ⇌ 2NO₂(g); δ. Η αντίδραση διάσπασης είναι ενδόθερμη ή εξώθερμη;	α. 6,5 . 10² Μ^-1 β. 28,08 . 10^-3 Μ. S^-1 γ. 9,3 . 10^-5 Μ, δ. ενδόθερμη
**59.	Σε κλειστό δοχείο όγκου 1 L έχουμε σε ισορροπία 4 mol N₂O₄ και 2 mol NO₂. Προσθέτουμε 10 mol αερίου He. Θα διαταραχθεί η ισορροπία N₂O₄(g) ⇌ 2NO₂(g), αν η θερμοκρασία παραμείνει σταθερή;	όχι

Aπαντήσεις στις ασκήσεις πολλαπλής επιλογής και σωστού λάθους

12. α. Σ, β. Λ, γ. Σ
13. δ
14. β
15. α. Λ, β. Σ, γ. Λ, δ. Σ
19. γ
21. α. αριστερά, β. αριστερά, γ. αριστερά
22. α. Σ, β. Λ, γ. Λ
23. β. δεξιά, γ. δεξιά, δ. δεξιά
24. β
25. β, δ
27. β
28. γ
33. β
36. δ: η ισορροπία μετατοπίζεται: i. δεξιά, ii. αριστερά, iii. δεξιά
41. β
51. i. γ, ii. β, iii. α
53. iii: α. αριστερά, β. δεξιά, γ. τίποτα

Δραστηριότητα

Η Αρχή Le Chatelier Και «Καθημερινή» Ζωή

Η ζωή μέσα μας και γύρω μας προχωρά ακολουθώντας κανόνες και αρχές. Αυτούς άλλωστε μελετούν συγγενείς επιστήμες όπως η Φυσική, η Χημεία, η Βιολογία. Βέβαια, μπορεί κανείς να ζει «ασυνείδητα» χωρίς να μπορεί να ερμηνεύει τον γύρω του κόσμο. Είναι όμως πολύ σημαντικό να μπορεί να παρατηρεί και να ερμηνεύει φαινόμενα που εξελίσσονται γύρω του βασισμένος σε μερικές βασικές αρχές. Μια τέτοια είναι και η Αρχή του Le Chatelier.
Εκείνο το οποίο ζητείται στο προκείμενο είναι να ερμηνευθούν με βάση αυτήν την αρχή μερικά γεγονότα όπως:
1. Όταν ένας άνθρωπος «της πόλης» κάνει διακοπές στο «βουνό» αποκτά μετά από κάποιες μέρες παραμονής ένα κόκκινο χρώμα, δηλωτικό κατά τα κλασικά καλής υγείας. Μπορείτε να εξηγήσετε το πού οφείλεται αυτό; Για την ερμηνεία χρησιμοποιήστε σαν βάση τον μηχανισμό της αναπνοής μέσω της δέσμευσης του Ο₂ της ατμόσφαιρας από την αιμοσφαιρίνη του αίματος, Hb. Aυτό είναι μια πολύπλοκη διαδικασία η οποία μπορεί να αποδοθεί από την ισορροπία : Hb(aq)+ Ο₂ (aq) ⇌ HbΟ₂(aq).
2. Η χημεία της δημιουργίας υπογείων σπηλαίων, σταλακτιτών και σταλαγμιτών είναι άλλη μια περίπτωση που ερμηνεύεται με την παραπάνω αρχή. Βρείτε τον μηχανισμό της δημιουργίας αυτών και γράψτε τις αντίστοιχες χημικές αντιδράσεις. Όπου μπορείτε, από την βιβλιογραφία, βρείτε και τις τιμές των σταθερών ισορροπίας των αντιδράσεων αυτών.
Υπάρχει στην περιοχή της Αττικής τέτοιο σπήλαιο; Τι είδους πετρώματα ευνοούν την δημιουργία τέτοιων σπηλαίων;
Σε ποια περίπτωση τέτοιες αποθέσεις όχι μόνο δεν έχουν τέτοιο αισθητικό αποτέλεσμα, αλλά προκαλούν ζημιές;

Εικόνα

4.3 Σταθερά χημικής ισορροπίας Κc - Κp

4.3 Σταθερά χημικής ισορροπίας Κ_c - Κ_p