3
ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ

Εικόνα

ΟΙ ΣΤΟΧΟΙ

Στο τέλος της διδακτικής αυτής ενότητας θα πρέπει να μπορείς:

Να αναφέρεις ποιο είναι το αντικείμενο μελέτης της χημικής κινητικής.
Να ορίζεις τι είναι μέση ταχύτητα αντίδρασης και τι στιγμιαία και να περιγράφεις τη διαδικασία που χρειάζεται για να προσδιοριστούν οι ταχύτητες αυτές πειραματικά.
Να καθορίζεις τους παράγοντες που επηρεάζουν την ταχύτητα της αντίδρασης και να εξηγείς την επίδραση αυτών στην ταχύτητα με βάση τη θεωρία των συγκρούσεων.
Να περιγράφεις τα χαρακτηριστικά που έχει ένας καταλύτης. Να ταξινομείς τους καταλύτες σε κατηγορίες, δίνοντας χαρακτηριστικά παραδείγματα σε κάθε περίπτωση.
Να εξηγείς τη δράση των καταλυτών με βάση τη θεωρία των ενδιάμεσων προϊόντων και τη θεωρία προσρόφησης και να αναφέρεις χαρακτηριστικά παραδείγματα εφαρμογών της κατάλυσης στη χημική βιομηχανία και βιοχημεία.
Να αναφέρεις το νόμο της ταχύτητας και να παράγεις αυτόν με βάση πειραματικά δεδομένα. Να συνδέεις το νόμο της ταχύτητας με το μηχανισμό της αντίδρασης.

ΠΕΡΙΕΧΟΜΕΝΑ

3.1	Γενικά για τη χημική κινητική και τη χημική αντίδραση-ταχύτητα αντίδρασης
3.2	Παράγοντες που επηρεάζουν την ταχύτητα αντίδρασης- Καταλύτες Μερικές εφαρμογές των ραδιοϊσοτόπων
3.3	Νόμος ταχύτητας- Μηχανισμός αντίδρασης
3.4	Ένα πείραμα χημικής κινητικής μελέτης
Ερωτήσεις - προβλήματα

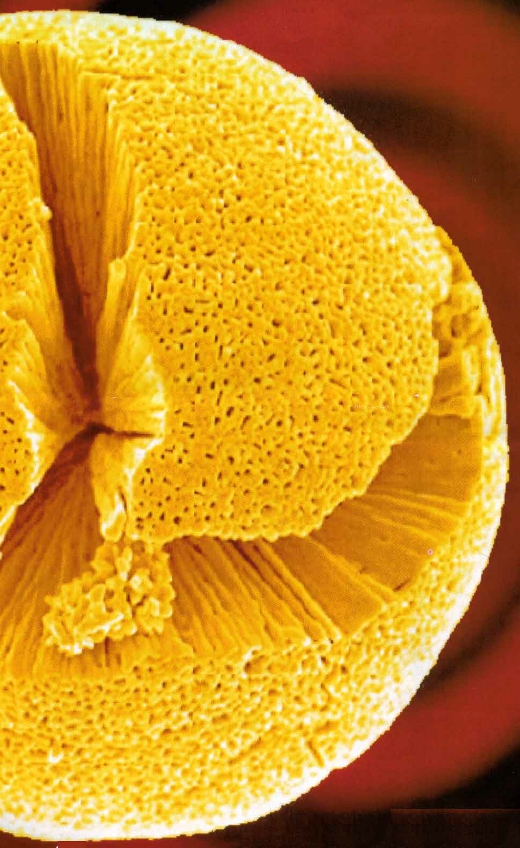Για να είναι ένας στερεός καταλύτης αποτελεσματικός, θα πρέπει να έχει μεγάλη επιφάνεια. Αυτό μπορούμε να το πετύχουμε παρασκευάζοντας τον καταλύτη υπό μορφή πολύ μικρών κόκκων. Οι σχετικές τεχνικές έχουν φτάσει στα όρια των δυνατοτήτων διαίρεσης της ύλης, στην κρυσταλλική κατάσταση, αφού μειώνονται οι διαστάσεις των κόκκων σε μεγέθη της τάξεως του νανόμετρου(10^-9 m). Οι «νανοδομές» αυτές δεν είναι δυνατόν να προκύψουν από λειοτρίβηση. Για παράδειγμα τo διοξείδιο του τιτανίου -TiO₂- παρασκευάζεται με εξάτμιση του μεταλλικού τιτανίου-Ti(s)- σε αδρανή ατμόσφαιρα υπό ελαττωμένη πίεση. Οι ατμοί του τιτανίου Ti(g)- συμπυκνώνονται σε επιφάνεια που διατηρείται σε θερμοκρασία υγρού αζώτου και στη συνέχεια οξειδώνονται προς TiO₂ . Στον κόσμο των «νανόκοκκων» παρουσιάζονται νέες συναρπαστικές ιδιότητες της ύλης. Μ΄ αυτή την μορφή το TiO₂ παρουσιάζει σπουδαία καταλυτική δράση, το οποίο δε συμβαίνει με το TiO₂ στην κανονική του μορφή. Στην εικόνα, φαίνεται η μικρογραφία ενός κόκκου τιτανίου, όπως έχει ληφθεί από ένα ηλεκτρονικό μικροσκόπιο. Η μορφολογία του κόκκου είναι σπογγώδης και είναι σύμφωνη με τη «Θεωρία Προσρόφησης» για την ερμηνεία της καταλυτικής δράσης.

3 ΧΗΜΙΚΗ ΚΙΝΗΤΙΚΗ

Εισαγωγή

Στην μέχρι τώρα γνωριμία μας με τη χημεία υπάρχει μια «σημαντική απουσία»: ο χρόνος… Είναι λοιπόν «καιρός» να μπει και ο χρόνος ως παράμετρος στη μελέτη ενός χημικού φαινομένου. Μάλιστα θα εστιάσουμε την προσπάθεια μας στην εξέταση της ταχύτητας ή καλύτερα του ρυθμού που εξελίσσεται μια χημική αντίδραση.
Καταρχάς, θα ορίσουμε τι είναι ταχύτητα μιας αντίδρασης και θα τη διακρίνουμε σε μέση και στιγμιαία ταχύτητα. Μετά θα προχωρήσουμε στους παράγοντες που την επηρεάζουν, θετικά ή αρνητικά, όπως είναι η θερμοκρασία και η συγκέντρωση των αντιδρώντων. Ειδικότερα, η επίδραση των συγκέντρωσης στην ταχύτητα θα εκφραστεί ποσοτικά μέσα από το νόμο της ταχύτητας. Κύριο χαρακτηριστικό του νόμου αυτού είναι ότι προκύπτει πειραματικά. Προσεκτική μάλιστα μελέτη της τάξης της αντίδρασης μπορεί να μας αποκαλύψει το μηχανισμό της, τα ενδιάμεσα, μη εμφανή, στάδια που ακολουθούνται μέχρις ότου τα αρχικά αντιδρώντα μεταπέσουν στα προϊόντα.
Οι καταλύτες και οι βιοκαταλύτες - ένζυμα και η επίδρασή τους πάνω στην ταχύτητα των αντιδράσεων εξετάζονται ιδιαίτερα. Η δράση τους στις χημικές, βιοχημικές, και στο συνδυασμό τους, τις αντιδράσεις βιοτεχνολογικής σημασίας, είναι από τα πιο σημαντικά θέματα του κεφαλαίου.
Πολλές από τις έννοιες που θα εισαχθούν - που δεν είναι και από τις πιο απλές - γίνονται ευκολότερα κατανοητές αν βάλει κανείς στο μυαλό του τη θεωρία των ενεργών συγκρούσεων. Σύγκρουση των μορίων των αντιδρώντων, κάτω από πολλές προϋποθέσεις, μπορεί να οδηγήσει στα προϊόντα. Και παράγοντες που κάνουν τη σύγκρουση αυτή πιο πιθανή και πιο «βίαιη» λογικά επιταχύνουν την αντίδραση.

3.1 Γενικά για τη χημική κινητική και τη χημική αντίδραση - Ταχύτητα αντίδρασης

Η χημεία μεταξύ άλλων καλείται να δώσει απάντηση στο βασικό ερώτημα, πόσο γρήγορα και από ποιους παράγοντες επηρεάζεται η ταχύτητα μιας αντίδρασης. Την απάντηση στο θέμα αυτό δίνει ο κλάδος της χημείας, χημική κινητική. Η χημική κινητική μεταξύ των άλλων μελετά την πορεία της αντίδρασης, δηλαδή τα βήματα που ακολουθεί η αντίδραση, ώστε τα αντιδρώντα να μεταβούν στα προϊόντα. Τα βήματα αυτά ονομάζονται στοιχειώδεις αντιδράσεις ή ενδιάμεσα στάδια και το σύνολό τους αποτελεί το μηχανισμό της αντίδρασης.

Η χημική κινητική μελετά

- Την ταχύτητα (ή το ρυθμό) που εξελίσσεται μια χημική αντίδραση.
- Τους παράγοντες που επηρεάζουν την ταχύτητα μιας αντίδρασης.
- Το μηχανισμό της αντίδρασης

Να παρατηρήσουμε ότι μια χημική εξίσωση, όπως π.χ.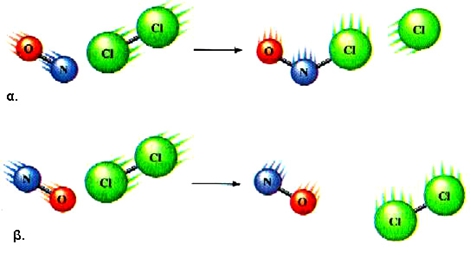
2H₂(g) + O₂(g) → 2H₂O(l) ΔΗ = -572 kJ,
μας πληροφορεί για την ανακατανομή ύλης και ενέργειας που λαμβάνει χώρα. Στο παράδειγμα, 2 mol H₂(g) αντιδρούν με 1 mol O₂(g) σχηματίζοντας 2 mol H₂O(l), ενώ παράλληλα ελευθερώνεται θερμότητα 572 kJ. Η χημική εξίσωση, όμως, δεν μας παρέχει κανένα στοιχείο, ούτε για την ταχύτητα, ούτε για το μηχανισμό της αντίδρασης. Η χημική κινητική αντλεί τα δεδομένα που χρειάζεται όχι από τη μορφή της εξίσωσης, αλλά από πειραματικές μετρήσεις, όπως είναι π.χ. ο προσδιορισμός της ποσότητας του εκλυόμενου αέριου προϊόντος σε συνάρτηση με το χρόνο.
Υπάρχουν αντιδράσεις που γίνονται ακαριαία και που δύσκολα μπορούμε να παρακολουθήσουμε την πορεία τους, όπως π.χ. η καύση του προπανίου:
C₃H₈(g) + 5O₂(g) → 3CO₂(g)+ 4H₂Ο(g)
Άλλες, πάλι, πραγματοποιούνται σε χιλιάδες χρόνια, όπως οι γεωλογικές μεταβολές. Εκτός απ’ αυτές, τις ακραίες περιπτώσεις, υπάρχουν αντιδράσεις που γίνονται σχετικά αργά, δηλαδή, σε χρόνους που επιτρέπουν τη μελέτη τους. Τέτοιες αντιδράσεις είναι για παράδειγμα η διάσπαση του ΗI:
2HΙ(g) → H₂(g) + I₂(g)
ή η εστεροποίηση:
CH₃COOH(l)+CH₃OH(l)→ CH₃COOCH₃(l)+ H₂O(l) .
Ωστόσο, να παρατηρήσουμε, ότι πολλά από τα θέματα που εξετάζει η χημική κινητική γίνονται ευκολότερα κατανοητά αν στηριχτούμε στη θεωρία των συγκρούσεων. Σύμφωνα με τη θεωρία αυτή, που πρότεινε ο Arrhenius το 1889, για να αντιδράσουν δύο μόρια πρέπει να συγκρουστούν αποτελεσματικά. Να έχουν δηλαδή, την κατάλληλη ταχύτητα και το σωστό προσανατολισμό . Αποτέλεσμα αυτής της σύγκρουσης είναι να «σπάσουν» οι αρχικοί δεσμοί των μορίων (αντιδρώντων) και να δημιουργηθούν νέοι (των προϊόντων). Η ελάχιστη τιμή ενέργειας, που πρέπει να έχουν τα μόρια, ώστε να αντιδράσουν αποτελεσματικά, ονομάζεται ενέργεια ενεργοποίησης
Όταν δύο αέρια αναμιχθούν σε ένα δοχείο, τότε ο αριθμός των συγκρούσεων μεταξύ των μορίων είναι τεράστιος. Απ’ αυτές έχει υπολογιστεί ότι μόνο το 1/10⁸ είναι αποτελεσματικές συγκρούσεις.

ΣΧΗΜΑ 3.1 Για να γίνει η αντίδραση NO+Cl2 → NOCl + Cl θα πρέπει τα αντιδρώντα μόρια να έχουν το σωστό προσανατολισμό και την κατάλληλη ταχύτητα. α: αποτελεσματική β: μη αποτελεσματική σύγκρουση.

ΣΧΗΜΑ 3.1 Για να γίνει η αντίδραση NO+Cl₂ → NOCl + Cl
θα πρέπει τα αντιδρώντα μόρια να έχουν το σωστό προσανατολισμό και την κατάλληλη ταχύτητα. α: αποτελεσματική β: μη αποτελεσματική σύγκρουση.

Arrhenius Σουηδός χημικός. Η θεωρία του σχετικά με τη διάσταση των ηλεκτρολυτών ήταν καρπός της διδακτορικής του διατριβής, η οποία σχεδόν απορρίφθηκε από τους εξεταστές του. Αργότερα, η θεωρία αυτή βραβεύτηκε με το Νόμπελ Χημείας το 1903. Σήμερα είναι γνωστός κυρίως από την εξίσωση που φέρει το όνομα του και η οποία συσχετίζει την ταχύτητα μιας αντίδρασης με τη θερμοκρασία.

• Έχει υπολογιστεί, σύμφωνα με την κινητική θεωρία των αερίων, ότι σε αέρια όγκου 1L σε STP συνθήκες γίνονται περίπου 10³² συγκρούσεις μορίων το δευτερόλεπτο.

Σύμφωνα με μια άλλη θεωρία, τη θεωρία της μεταβατικής κατάστασης, για να πραγματοποιηθεί μια αντίδραση θα πρέπει να σχηματιστεί κατά τη σύγκρουση των αντιδρώντων ένα ενδιάμεσο προϊόν. Το προϊόν αυτό απορροφά την ενέργεια ενεργοποίησης και ονομάζεται ενεργοποιημένο σύμπλοκο.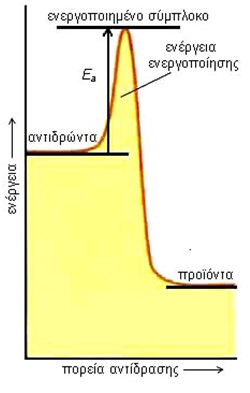

ΣΧΗΜΑ 3.2 Για να πραγματοποιηθεί μια αντίδραση θα πρέπει τα αντιδρώντα μόρια να έχουν μια ελάχιστη τιμή ενέργειας (ενέργεια ενεργοποίησης, Εa).

Ταχύτητα αντίδρασης - Ορισμός

Ας πάρουμε για παράδειγμα την αντίδραση:
2ΗI(g) → H₂(g) + I₂(g)
Η ταχύτητα διάσπασης του HΙ (ή καλύτερα ο ρυθμός μεταβολής της συγκέντρωσης του ΗI) δίνεται από τη σχέση:
Εικόνα
Το αρνητικό πρόσημο εισάγεται, ώστε η ταχύτητα διάσπασης, δηλαδή ο ρυθμός μεταβολής της συγκέντρωσης του ΗΙ, να πάρει θετικές τιμές.

Στην ίδια αντίδραση η ταχύτητα σχηματισμού του Η₂ και του Ι₂ (ή καλύτερα ο ρυθμός μεταβολής της συγκέντρωσης των Η₂ και Ι₂) είναι:

Για να γίνει μια χημική αντίδραση Α → Β χρειάζεται ένα ελάχιστο ποσό ενέργειας, που ονομάζεται ενέργεια ενεργοποίησης.

Εικόνα

Σύμφωνα με τη στοιχειομετρία της παραπάνω χημικής εξίσωσης, αν σε χρονικό διάστημα Δt αντιδράσουν χ mol HI σχηματίζονται χ/2 mol H₂ και χ/2 mol I₂. Έτσι, εύκολα μπορούμε να διαπιστώσουμε ότι:
υ_HI = 2 υ_H₂ = 2 υ_I₂

Δηλαδή ο ρυθμός μεταβολής της συγκέντρωσης του ΗΙ είναι διπλάσιος του αντίστοιχου του Η₂ και Ι₂.

Γενικά ορίζεται ταχύτητα υ μιας χημικής αντίδρασης της μορφής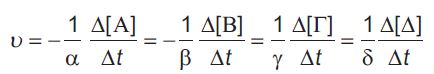
αΑ + βΒ → γΓ + δΔ :

Έτσι, η ταχύτητα της αντίδρασης 2ΗΙ(g) → H₂(g) + I₂(g) είναι:
Εικόνα

Να σημειωθεί ότι η ταχύτητα της αντίδρασης δεν είναι σταθερή καθ’ όλη τη διάρκεια της. Στην αρχή (εκτός ελαχίστων εξαιρέσεων) η ταχύτητα είναι η μέγιστη. Ελαττώνεται, όμως, με την πάροδο του χρόνου, καθώς μειώνεται η συγκέντρωσης των αντιδρώντων, ώσπου στο τέλος να μηδενιστεί. Είναι λοιπόν αυτονόητο, ότι οι μετρήσεις μεταβολών συγκεντρώσεων αντιδρώντων ή προϊόντων σε κάποιο χρονικό διάστημα , Δt, αφορούν τον προσδιορισμό της μέσης ταχύτητας της αντίδρασης για το χρονικό αυτό διάστημα.

Στιγμιαία ταχύτητα χημικής αντίδρασης, που έχει τη γενική μορφή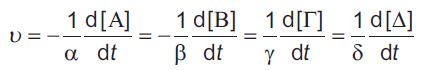
αΑ + βΒ → γΓ + δΔ ,
ορίζεται ως:

όπου dc είναι μια απειροελάχιστη μεταβολή της συγκέντρωσης c, κατά την απειροελάχιστη μεταβολή dt του χρόνου στη χρονική στιγμή t.
Η καμπύλη αντίδρασης μας δείχνει πως μεταβάλλεται η συγκέντρωση ενός από τα αντιδρώντα ή τα προϊόντα με το χρόνο. Με βάση την καμπύλη αντίδρασης, που προκύπτει πειραματικά, μπορούμε να υπολογίσουμε τη στιγμιαία ταχύτητα της αντίδρασης κάποια χρονική στιγμή t₁, ακολουθώντας τη διαδικασία που περιγράφεται στο παρακάτω σχήμα:

Διαγραμματική απεικόνιση της πορείας μιας υποθετικής αντίδρασης της μορφής: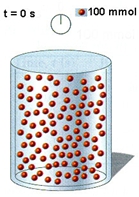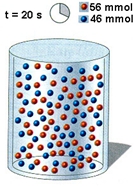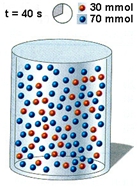
Α(g) → Β(g)
και υπολογισμός της ταχύτητας αυτής.

V_δοχ= 1 L

1. Ρυθμός μεταβολής της συγκέντρωσης του Β την περίοδο 0 - 20 s
υ _B = Δ[B] /Δt =(46-0) /20 =
= 2,3 mmol L^-1 s^-1

2. Ρυθμός μεταβολής της συγκέντρωσης του Β την περίοδο 20 - 40 s
υ _B = Δ[B] /Δt =(70-46) /20 =
= 1,2 mmol L^-1 s^-1

3. Ρυθμός μεταβολής της συγκέντρωσης του Β την περίοδο 0 - 40 s
υ _B = Δ[B] /Δt =(70-0) /40 =
= 1,75 mmol L^-1 s^-1

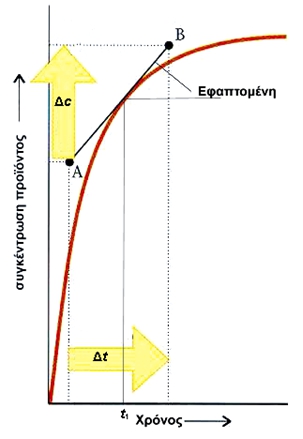ΣΧΗΜΑ 3.3 Για να υπολογίσουμε τη στιγμιαία ταχύτητα τη χρονική στιγμή t1, φέρνουμε την εφαπτομένη της καμπύλης που αντιστοιχεί στο σημείο t1 και υπολογίζουμε τη κλίση της. Η κλίση της ευθείας αυτής βρίσκεται αν πάρουμε δύο σημεία της Α και Β και υπολογίσουμε το Δc και Δ t. Η στιγμιαία ταχύτητα υ t1 τη χρονική στιγμή t1 δίνεται από τη σχέση: υ t1 = Δc/Δt

ΣΧΗΜΑ 3.3 Για να υπολογίσουμε τη στιγμιαία ταχύτητα τη χρονική στιγμή t₁, φέρνουμε την εφαπτομένη της καμπύλης που αντιστοιχεί στο σημείο t₁ και υπολογίζουμε τη κλίση της. Η κλίση της ευθείας αυτής βρίσκεται αν πάρουμε δύο σημεία της Α και Β και υπολογίσουμε το Δc και Δ t. Η στιγμιαία ταχύτητα σχηματισμού προιόντος υ _t₁ τη χρονική στιγμή t₁ δίνεται από τη σχέση: υ _t1 = Δc/Δt

Παράδειγμα 3.1

Η ταχύτητα σχηματισμού της ΝΗ₃ Ν₂(g) + 3H₂(g) → 2NH₃(g) είναι 2,5 mol L^-1 h^-1. α) Ποιος είναι ο ρυθμός κατανάλωσης του Η₂ στο ίδιο χρονικό διάστημα; β) Ποια είναι η ταχύτητα της αντίδρασης;

ΛΥΣΗ
α) Από της αντίδραση εύκολα υπολογίζουμε ότι:
Ν₂ + 3Η₂ → 2ΝΗ₃
Εικόνα
άρα ο ρυθμός κατανάλωση του Η₂ είναι 3,75 mol L^-1 h^-1.
β) Η ταχύτητα της αντίδρασης είναι:

Εφαρμογή

Ο ρυθμός σχηματισμού του HI, Η₂ + I₂ → 2HI είναι 0,04 mol L^-1s^-1.
α) Ποιος είναι ο ρυθμός κατανάλωσης του Η₂ στο ίδιο χρονικό διάστημα;
β) Ποια είναι η ταχύτητα της αντίδρασης;

(α. 0,02 mol L^-1 s^-1 β. 0,02 mol L^-1 s^-1)

Πειραματικός προσδιορισμός της ταχύτητας της αντίδρασης: 2H₂O₂(l) → 2H₂O(l) + O₂(g)
Αυτό γίνεται με μέτρηση της μάζας του ελευθερωμένου O₂ σε συνάρτηση με το χρόνο. Ο προσδιορισμός αυτός γίνεται έμμεσα με μέτρηση της μάζας του αντιδρώντος συστήματος, η οποία μειώνεται με την πάροδο του χρόνου, λόγω έκλυσης του Ο₂(g).

α. t = 0 s, m = 1246,050 g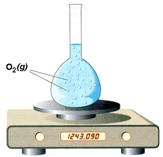

β. t = 60 s, m = 1243,090 g

Παράδειγμα 3.2

Η συγκέντρωση του αιθυλενίου CH₂ = CH₂ στην αντίδραση:
2CH₂ = CH₂(g) → C₄H₈ μεταβάλλεται συναρτήσει του χρόνου στους
900 K, όπως δείχνει ο ακόλουθος πίνακας:

χρόνος /s	0	10	20	40	60	100
[C₂H₄] / molL^-1	0,91	0,65	0,51	0,34	0,28	0,19

α. Να βρεθεί η μέση ταχύτητα της αντίδρασης για τα πρώτα 20 s.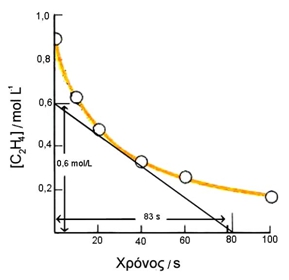
β. Να βρεθεί η ταχύτητα 30 s μετά την έναρξη των μετρήσεων.

ΛΥΣΗ
α. Για τα πρώτα 20 s εύκολα υπολογίζουμε ότι:
Εικόνα
β. Σχεδιάζουμε την καμπύλη μεταβολής της συγκεντρώσεως C₂H₄ συναρτήσει του χρόνου

Από την καμπύλη της αντίδρασης υπολογίζουμε την ταχύτητα της αντίδρασης 30s μετά την έναρξη των μετρήσεων
Εικόνα

Εφαρμογή

Η κινητική μελέτη της αντίδρασης 2Α → Β + 3Γ οδήγησε στον παρακάτω πίνακα μετρήσεων:

χρόνος /min	0	2	4	6
c_A / mol L^-1	6	4	3	2,6

α. Να βρεθεί η μέση ταχύτητα της αντίδρασης στα πρώτα 2 min.
β. Να βρεθεί η ταχύτητα 5 min μετά την έναρξη της αντίδρασης .

(α. 2 mol L^-1 min^-1)