| ΘΕΡΜΟΔΥΝΑΜΙΚΗ | 2 |
 |
|
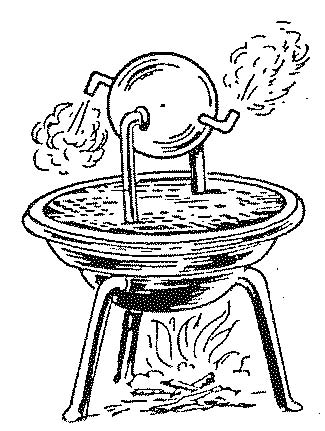 Εικ. 2.1 Σχέδιο του ατμοστρόβιλου που επινόησε ο αρχαίος έλληνας εφευρέτης Ήρων (Αλεξάνδρεια, περ. 100 μ.Χ.). Το δοχείο είναι κλειστό και επικοινωνεί με τη σφαίρα με τους δύο κατακόρυφους σωλήνες. Με βρασμό νερού παράγεται ατμός στο δοχείο που εισέρχεται από τους σωλήνες στη σφαίρα και εξέρχεται με μεγάλη ταχύτητα από τα δύο ακροφύσια θέτοντας σε περιστροφή τη σφαίρα. Εικ. 2.1 Σχέδιο του ατμοστρόβιλου που επινόησε ο αρχαίος έλληνας εφευρέτης Ήρων (Αλεξάνδρεια, περ. 100 μ.Χ.). Το δοχείο είναι κλειστό και επικοινωνεί με τη σφαίρα με τους δύο κατακόρυφους σωλήνες. Με βρασμό νερού παράγεται ατμός στο δοχείο που εισέρχεται από τους σωλήνες στη σφαίρα και εξέρχεται με μεγάλη ταχύτητα από τα δύο ακροφύσια θέτοντας σε περιστροφή τη σφαίρα. |
2-1 ΕΙΣΑΓΩΓΗ
Ο όρος θερμοδυναμική προέρχεται από τις ελληνικές λέξεις θερμότητα και δύναμη. Αν και η πρώτη θερμική μηχανή, που είναι ιστορικά γνωστή, κατασκευάστηκε από τον Ήρωνα τον Αλεξανδρινό περίπου το 100 μ.Χ., αφετηρία για την ανάπτυξη της θερμοδυναμικής στάθηκε η εφεύρεση της ατμομηχανής και οι προσπάθειες που ακολούθησαν για τη βελτίωση και τελειοποίηση των μηχανών που μετέτρεπαν τη θερμότητα σε ωφέλιμο έργο. Η θερμοδυναμική μελετάει τη μετατροπή της θερμότητας σε μηχανικό έργο και τους περιορισμούς που η φύση έχει επιβάλει. Από την εποχή που εφευρέθηκε η πρώτη ατμομηχανή μέχρι σήμερα έχουν περάσει πολλά χρόνια. Η πρόοδος της θερμοδυναμικής οδήγησε στην κατασκευή όλων των σύγχρονων θερμικών μηχανών, βενζινοκινητήρων, πετρελαιοκινητήρων, κινητήρων αεροσκαφών, ατμοστρόβιλων.
2-2 ΘΕΡΜΟΔΥΝΑΜΙΚΟ ΣΥΣΤΗΜΑ
Στο κεφάλαιο αυτό θα χρησιμοποιούμε συχνά τον όρο θερμοδυναμικό σύστημα. Γενικά, σύστημα είναι ένα τμήμα του φυσικού κόσμου που διαχωρίζεται από τον υπόλοιπο κόσμο με πραγματικά ή νοητά τοιχώματα. Ο υπόλοιπος φυσικός κόσμος αποτελεί το περιβάλλον του συστήματος.
Αν κατά τη μελέτη ενός συστήματος, για την περιγραφή του χρησιμοποιούμε μόνο μεγέθη της μηχανικής, π.χ. δύναμη, ταχύτητα, επιτάχυνση, ορμή κ.λ.π. το σύστημα χαρακτηρίζεται μηχανικό. Στην περίπτωση που για την περιγραφή του χρησιμοποιούνται και θερμοδυναμικά μεγέθη, όπως θερμότητα, θερμοκρασία, εσωτερική ενέργεια και άλλα, το σύστημα χαρακτηρίζεται θερμοδυναμικό.
Εμείς θα ασχοληθούμε με τα απλούστερα θερμοδυναμικά συστήματα, δηλαδή αέρια που βρίσκονται μέσα σε δοχεία στο εσωτερικό των οποίων δε γίνονται χημικές αντιδράσεις. Ένα τέτοιο σύστημα θα χαρακτηρίζεται θερμικά μονωμένο ή απλά μονωμένο αν τα τοιχώματα του δοχείου δεν επιτρέπουν τη μεταφορά θερμότητας από το αέριο προς το περιβάλλον ή αντίστροφα.
2-3 ΙΣΟΡΡΟΠΙΑ ΘΕΡΜΟΔΥΝΑΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ
Για να περιγραφεί ένα θερμοδυναμικό σύστημα χρειάζεται να γνωρίζουμε κάποια στοιχεία του. Για παράδειγμα, ορισμένη ποσότητα αερίου που βρίσκεται σε ένα δοχείο μπορεί να περιγραφεί αν γνωρίζουμε τον όγκο του, τη θερμοκρασία του και την πίεσή του. Τα στοιχεία αυτά ονομάζονται θερμοδυναμικές μεταβλητές. |
Ο όγκος, η πίεση και η θερμοκρασία ορισμένης ποσότητας αερίου σχετίζονται μεταξύ τους με την καταστατική εξίσωση. Για να περιγράψουμε την κατάσταση συγκεκριμένης ποσότητας αερίου αρκούν δύο από αυτά αφού το τρίτο προκύπτει από την καταστατική εξίσωση. Οι δύο ποσότητες που είναι ικανές για την περιγραφή της κατάστασης ορισμένης ποσότητας αερίου αποτελούν τις ανεξάρτητες θερμοδυναμικές μεταβλητές του συστήματος.
Όταν σ’ ένα θερμοδυναμικό σύστημα οι θερμοδυναμικές μεταβλητές που το περιγράφουν διατηρούνται σταθερές με το χρόνο, το σύστημα βρίσκεται σε κατάσταση θερμοδυναμικής ισορροπίας. Σε αντίθετη περίπτωση το σύστημα μεταβάλλεται. Ειδικότερα, λέμε ότι
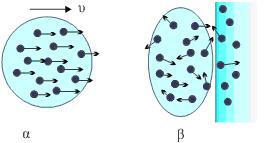
μια ποσότητα αερίου βρίσκεται σε κατάσταση θερμοδυναμικής ισορροπίας - ή απλά ισορροπίας - όταν η πίεση (p), η πυκνότητα (ρ) η θερμοκρασία του (Τ) έχουν την ίδια τιμή σε όλη την έκταση του αερίου.

Η κατάσταση θερμοδυναμικής ισορροπίας ενός αερίου μπορεί να παρασταθεί γραφικά με ένα σημείο σε σύστημα συντεταγμένων με άξονες δύο ανεξάρτητες θερμοδυναμικές μεταβλητές του συστήματος. Αν το σύστημα δε βρίσκεται σε ισορροπία η κατάστασή του δε μπορεί να αποδοθεί γραφικά αφού δε μπορούμε να μιλήσουμε για πίεση ή θερμοκρασία του συστήματος. Η πίεση και η θερμοκρασία έχουν διαφορετικές τιμές στα διάφορα σημεία του αερίου.
Η κατάσταση θερμοδυναμικής ισορροπίας ενός συστήματος μπορεί να παρασταθεί γραφικά με ένα σημείο. Ένα σύστημα που δε βρίσκεται σε ισορροπία δεν παριστάνεται γραφικά.
2-4 ΑΝΤΙΣΤΡΕΠΤΕΣ ΜΕΤΑΒΟΛΕΣ
Όταν σε ένα θερμοδυναμικό σύστημα πραγματοποιείται μια μεταβολή αλλάζουν τόσο το σύστημα όσο και το περιβάλλον του συστήματος.
Αντιστρεπτή ονομάζεται εκείνη η μεταβολή κατά την οποία υπάρχει η δυνατότητα επαναφοράς του συστήματος και του περιβάλλοντος στην αρχική τους κατάσταση. |
Σχ. 2.1 (α) Το αέριο βρίσκεται σε κατάσταση θερμοδυναμικής ισορροπίας. β) Το αέριο δε βρίσκεται σε κατάσταση θερμοδυναμικής ισορροπίας. Η θερμοκρασία, η πίεση και η πυκνότητα δεν έχουν την ίδια τιμή σε όλη του την έκταση. (γ) Το αέριο βρίσκεται σε νέα κατάσταση ισορροπίας.
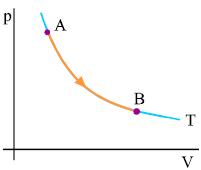
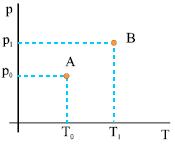 Σχ. 2.2 Η αρχική κατάστασή του αερίου του σχήματος 2.1 παριστάνεται με ένα σημείο το Α και η τελική κατάστασή του, που είναι κατάσταση ισορροπίας, με το σημείο Β. Σχ. 2.2 Η αρχική κατάστασή του αερίου του σχήματος 2.1 παριστάνεται με ένα σημείο το Α και η τελική κατάστασή του, που είναι κατάσταση ισορροπίας, με το σημείο Β. |
Εικ. 2.2 Για το αβγό της φωτογραφίας δεν υπάρχει καμιά δυνατότητα να επανέλθει στην αρχική του κατάσταση.
Σχ. 2.3 Πιέζουμε απότομα το έμβολο ώστε το αέριο να μεταβεί στην κατάσταση Β. Η μεταβολή δεν είναι αντιστρεπτή. Στο διάγραμμα μπορεί να παρασταθεί μόνο η αρχική και η τελική κατάσταση του αερίου |
Οι μεταβολές στη φύση δεν είναι αντιστρεπτές. Η αντίστροφη πορεία ενός φαινομένου είναι αυτό που θα βλέπαμε εάν κινηματογραφούσαμε το φαινόμενο και παίζαμε την ταινία ανάποδα -προς τα πίσω. Εάν κινηματογραφούσαμε ένα κερί που καίγεται θα ήταν αποδεκτή η αντίστροφη πορεία, δηλαδή ένα κερί που το μήκος του αυξάνεται; Η αντίστροφη πορεία στην ανάπτυξη ενός φυτού θα ήταν το φυτό να μικραίνει μέχρι να ξαναγίνει σπόρος. Είμαστε τόσο εξοικειωμένοι με τη μη αντιστρεπτότητα των μεταβολών στη φύση ώστε η αντίστροφη πορεία ενός φαινομένου φαίνεται να παραβιάζει την κοινή λογική.

Όμως, η έννοια της αντιστρεπτής μεταβολής είναι χρήσιμη. Έστω λοιπόν, ένα αέριο που βρίσκεται μέσα σε κύλινδρο. Ο κύλινδρος κλείνεται στο πάνω μέρος του με εφαρμοστό έμβολο. Το αέριο μέσα στο δοχείο βρίσκεται σε ισορροπία. Η θερμοκρασία του είναι ΤΑ, ο όγκος που καταλαμβάνει VA και η πίεση που ασκεί pA. Θα μεταβάλουμε την κατάσταση του αερίου ώστε ο όγκος του να μειωθεί σε VB και η πίεση και η θερμοκρασία να πάρουν τελικά τις τιμές pB και TB. Από τους πολλούς τρόπους με τους οποίους μπορεί να πραγματοποιηθεί η μεταβολή επιλέγουμε δυο ακραίες περιπτώσεις: Στην πρώτη πιέζουμε απότομα το έμβολο ώστε ο όγκος του αερίου να μειωθεί στην επιθυμητή τιμή και περιμένουμε μέχρι να αποκατασταθεί ισορροπία στο αέριο. Στη διάρκεια της μεταβολής αυτής το αέριο βρίσκεται σε αναταραχή, η πίεση και η θερμοκρασία του δεν είναι ίδιες σε όλη την έκτασή του και επομένως δε μπορούμε να παραστήσουμε τη μεταβολή σε διάγραμμα. Σε διάγραμμα μπορεί να παρασταθεί μόνο η αρχική και η τελική κατάσταση του αερίου, που είναι καταστάσεις ισορροπίας.

|
Στη δεύτερη περίπτωση ρίχνουμε πρώτα λίγους κόκκους άμμου πάνω στο έμβολο. Αυτό θα μειώσει ελάχιστα τον όγκο του αερίου. Περιμένουμε λίγο ώστε να ισορροπήσει το αέριο. Η νέα κατάσταση ισορροπίας βρίσκεται πολύ κοντά στη αρχική. Αν απεικονίζαμε γραφικά τη νέα κατάσταση ισορροπίας θα προέκυπτε ένα σημείο πολύ κοντά στο σημείο που απεικονίζει την αρχική κατάσταση ισορροπίας. Στη συνέχεια ρίχνουμε πάλι λίγους κόκκους άμμου πάνω στο έμβολο, μειώνοντας ακόμα λίγο τον όγκο, περιμένουμε πάλι να αποκατασταθεί κατάσταση ισορροπίας, κ.ο.κ. Επαναλαμβάνοντας συνεχώς αυτή τη διαδικασία φέρνουμε το σύστημα στην τελική κατάσταση.
Κατά τη διάρκεια αυτής της μεταβολής το σύστημα περνάει από διαδοχικές καταστάσεις που μπορούμε να τις θεωρήσουμε καταστάσεις ισορροπίας.
Κάθε μια από αυτές μπορεί να παρασταθεί γραφικά με ένα σημείο. Εφόσον η μια κατάσταση ισορροπίας διαδέχεται την άλλη, τα σημεία στο διάγραμμα θα βρίσκονται το ένα δίπλα στο άλλο με αποτέλεσμα να δημιουργείται μια γραμμή που ξεκινάει από την αρχική κατάσταση και οδηγεί στην τελική. Με αντίστροφους χειρισμούς, αφαιρώντας δηλαδή άμμο από το έμβολο, το σύστημα θα οδηγηθεί πάλι στην αρχική του κατάσταση.

Η μεταβολή που περιγράψαμε αποτελεί μια εξιδανίκευση, δεν είναι δυνατόν ένα σύστημα να βρίσκεται διαρκώς σε ισορροπία και ταυτόχρονα σιγά - σιγά να μεταβάλλεται.
Μια τέτοια εξιδανικευμένη μεταβολή κατά την οποία ένα σύστημα μεταβαίνει από μια αρχική κατάσταση σε μια τελική μέσω διαδοχικών καταστάσεων ισορροπίας θα την ονομάζουμε αντιστρεπτή. Μια τέτοια μεταβολή είναι δυνατόν να πραγματοποιηθεί και αντίστροφα.
Μια αντιστρεπτή μεταβολή παριστάνεται γραφικά με μια συνεχή γραμμή. Οι μη αντιστρεπτές μεταβολές δε μπορούν να παρασταθούν γραφικά.
|
Σχ. 2.4 Προσθέτουμε στο έμβολο αργά κόκκους άμμου μέχρι το αέριο να φτάσει στην τελική κατάσταση Β. Το αέριο μεταβαίνει από την κατάσταση Α στη Β μέσω διαδοχικών καταστάσεων που μπορούν να θεωρηθούν καταστάσεις ισορροπίας. Η μεταβολή αυτή είναι αντιστρεπτή και παριστάνεται με μια γραμμή που οδηγεί από την αρχική στην τελική κατάσταση. |
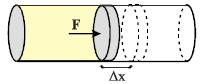 Σχ. 2.5 Το αέριο εκτονώνεται και το έμβολο μετατοπίζεται κατά Δx. Η δύναμη F που ασκεί το αέριο στο έμβολο παράγει έργο ΔW. Σχ. 2.5 Το αέριο εκτονώνεται και το έμβολο μετατοπίζεται κατά Δx. Η δύναμη F που ασκεί το αέριο στο έμβολο παράγει έργο ΔW.
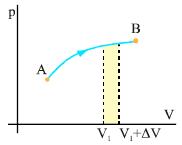 Σχ. 2.6 Σε μια τυχαία αντιστρεπτή μεταβολή το έργο κατά την εκτόνωση του αερίου από όγκο V1 σε όγκο V1+ΔV είναι ίσο με το εμβαδόν της επιφάνειας με το κίτρινο χρώμα. Σχ. 2.6 Σε μια τυχαία αντιστρεπτή μεταβολή το έργο κατά την εκτόνωση του αερίου από όγκο V1 σε όγκο V1+ΔV είναι ίσο με το εμβαδόν της επιφάνειας με το κίτρινο χρώμα.
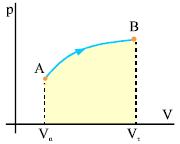 Σχ. 2.7 Σε μια τυχαία αντιστρεπτή μεταβολή το έργο του αερίου κατά τη μεταβολή του από το Α στο Β είναι ίσο με το εμβαδόν κάτω από την γραμμή του διαγράμματος. Σχ. 2.7 Σε μια τυχαία αντιστρεπτή μεταβολή το έργο του αερίου κατά τη μεταβολή του από το Α στο Β είναι ίσο με το εμβαδόν κάτω από την γραμμή του διαγράμματος.
|
2-5 ΕΡΓΟ ΠΑΡΑΓΟΜΕΝΟ ΑΠΟ ΑΕΡΙΟ ΚΑΤΑ ΤΗ
ΔΙΑΡΚΕΙΑ ΜΕΤΑΒΟΛΩΝ ΟΓΚΟΥ Έστω ένα αέριο σε κύλινδρο που κλείνεται από εφαρμοστό έμβολο. Οι μηχανές εσωτερικής καύσης, οι ατμομηχανές, οι συμπιεστές στα ψυγεία και τα κλιματιστικά μηχανήματα χρησιμοποιούν κάποια παραλλαγή τέτοιου συστήματος. Καθώς τα μόρια του αερίου μέσα στον κύλινδρο συγκρούονται με τα τοιχώματα του κυλίνδρου ασκούν δυνάμεις σ΄ αυτά. Έστω F η ολική δύναμη που ασκεί το αέριο στο έμβολο. Αν το έμβολο μετακινηθεί προς τα έξω κατά την πολύ μικρή απόσταση Δx, το έργο που παράγει η δύναμη που ασκεί το αέριο είναι:
Αν το εμβαδόν του εμβόλου είναι Α και η πίεση του αερίου p, ισχύει
και η σχέση (2.1) γίνεται
Όμως A Δx = ΔV όπου ΔV η πολύ μικρή μεταβολή του όγκου του αερίου. Έτσι μπορούμε να εκφράσουμε το έργο που παράγει το αέριο
Σύμφωνα με τη σχέση (2.3) το έργο είναι θετικό αν το αέριο εκτονώνεται (αυξάνει ο όγκος του) και αρνητικό αν το αέριο συμπιέζεται. Προσοχή: στο έμβολο μπορεί να ασκούνται και πολλές άλλες δυνάμεις. Η σχέση (2.3) δίνει το έργο της δύναμης που ασκεί το αέριο.
Έστω τώρα μια τυχαία αντιστρεπτή μεταβολή κατά την οποία το αέριο μεταβαίνει από την αρχική κατάσταση Α στην τελική κατάσταση Β (σχ.2.6). Αν η βάση (ΔV) της επιφάνειας με το κίτρινο χρώμα στο σχήμα 2.6 είναι πολύ μικρή, η επιφάνεια μπορεί να θεωρηθεί παραλληλόγραμμο. Το εμβαδόν της, που ισούται με το γινόμενο βάση x ύψος = ΔV·ΔW, δίνει το έργο του αερίου κατά την εκτόνωσή του, από όγκο V1 σε όγκο V1+ΔV.
Αν χωρίσουμε την επιφάνεια κάτω από τη γραμμή του διαγράμματος σε στοιχειώδεις τέτοιες επιφάνειες και αθροίσουμε τα εμβαδά θα πάρουμε το έργο του αερίου κατά την μεταβολή του από την κατάσταση Α στην κατάσταση Β (σχ. 2.7).
Το έργο ενός αερίου σε μια αντιστρεπτή μεταβολή είναι αριθμητικά ίσο με το εμβαδόν της επιφάνειας από την γραμμή του διαγράμματος μέχρι τον άξονα V, στο διάγραμμα p-V.
|
2-6 ΘΕΡΜΟΤΗΤΑ
Αν έρθουν σε επαφή δύο σώματα με διαφορετικές θερμοκρασίες Τ1 και Τ2
H ενέργεια που μεταφέρεται λόγω της διαφοράς θερμοκρασίας δύο σωμάτων ονομάζεται θερμότητα και συμβολίζεται με Q.
H θερμότητα, ως μορφή ενέργειας, στο SI μετριέται σε Joule. Πιο συνηθισμένη μονάδα της είναι η θερμίδα (cal από το calorie).
Σημείο εκκίνησης της κινητικής θεωρίας είναι η υπόθεση ότι τα αέρια αποτελούνται από πολύ μεγάλο πλήθος απειροελάχιστων σφαιριδίων που κινούνται τυχαία (άτακτα) μέσα στο χώρο που καταλαμβάνει το αέριο. Τα σφαιρίδια αυτά δεν είναι τίποτε άλλο από αυτό που σήμερα αποτελεί για τον καθένα κοινό τόπο, τα μόρια του αερίου.
Προσοχή: Η θερμότητα δεν πρέπει να συγχέεται με τη θερμοκρασία. Η θερμότητα είναι ενέργεια ενώ η θερμοκρασία είναι το μέγεθος που επινοήσαμε για να μετράμε αντικειμενικά πόσο ζεστό ή κρύο είναι ένα σώμα.
2-7 ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ
Ένα αέριο σε υψηλή πίεση έχει τη δυνατότητα να παράγει έργο, επομένως το αέριο εμπεριέχει ενέργεια. Την ενέργεια αυτή θα την ονομάσουμε εσωτερική ενέργεια (συμβολίζεται με U), για να τη διακρίνουμε από οποιαδήποτε εξωτερική ενέργεια μπορεί να έχει το αέριο (π.χ. το αέριο μπορεί να έχει και κινητική ενέργεια λόγω μεταφορικής κίνησης που εκτελεί το δοχείο μέσα στο οποίο βρίσκεται).
Από μικροσκοπική άποψη, η ενέργεια που εμπεριέχει ένα σύστημα οφείλεται στην ενέργεια που έχουν τα σωματίδια που το απαρτίζουν. Τα μόρια, τα άτομα ή τα ιόντα οποιουδήποτε σώματος, σε όποια φάση και αν βρίσκεται (στερεή, υγρή ή αέρια) διαρκώς κινούνται. Έχουν επομένως κινητική ενέργεια. Επιπλέον, στα στερεά και στα υγρά τα σωματίδια αλληλεπιδρούν μεταξύ τους, επομένως έχουν και δυναμική ενέργεια.
Κάθε σώμα εμπεριέχει ενέργεια, που είναι το άθροισμα των ενεργειών των σωματιδίων που το απαρτίζουν, ως αποτέλεσμα της σχετικής τους κίνησης ως προς το κέντρο μάζας του σώματος και των αλληλεπιδράσεων μεταξύ τους. Αυτή την ενέργεια την ονομάζουμε εσωτερική ενέργεια.
Η εσωτερική ενέργεια ιδανικού αερίου
Τα μόρια του ιδανικού αερίου δεν αλληλεπιδρούν μεταξύ τους, επομένως δεν έχουν δυναμική ενέργεια. Η εσωτερική ενέργεια ενός ιδανικού αερίου οφείλεται στις κινητικές ενέργειες που έχουν τα μόριά του και είναι ίση με το άθροισμα αυτών των ενεργειών. Η εσωτερική ενέργεια ενός ιδανικού αερίου είναι δυνατό να υπολογιστεί. |
|
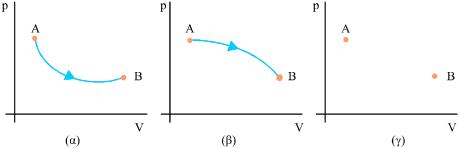
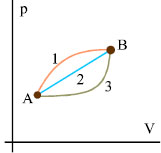
Σχ. 2.8 Στα (α) και (β) ένα αέριο σύστημα μεταβαίνει από την κατάσταση Α στη Β με, διαφορετικό κάθε φορά, αντιστρεπτό τρόπο. Στο (γ) το ίδιο σύστημα μεταβαίνει από την κατάσταση Α στη Β με μη αντιστρεπτό τρόπο. Η μεταβολή δεν μπορεί να παρασταθεί γραφικά. Η μεταβολή της εσωτερικής ενέργειας του συστήματος είναι ίδια σε όλες τις περιπτώσεις.
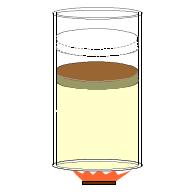 Σχ. 2.9 Ποσότητα αέριου θερμαίνεται. Το αέριο κατά την διάρκεια της μεταβολής του παράγει έργο. Σχ. 2.9 Ποσότητα αέριου θερμαίνεται. Το αέριο κατά την διάρκεια της μεταβολής του παράγει έργο. |
Η μέση κινητική ενέργεια ενός μορίου ιδανικού αερίου υπολογίστηκε στην παράγραφο 1-5 και βρέθηκε Αν το αέριο περιέχει Ν μόρια, η εσωτερική του ενέργεια θα είναι
Αλλά Ν = n ΝΑ όπου n ο αριθμός των mol του αερίου. Επομένως
Η (2.5) δείχνει ότι η εσωτερική ενέργεια ορισμένης ποσότητας ιδανικού αερίου εξαρτάται μόνο από τη θερμοκρασία του.
Έστω ένα ιδανικό αέριο που βρίσκεται αρχικά σε ισορροπία στην κατάσταση Α. Αν το αέριο μεταβεί σε μια άλλη κατάσταση ισορροπίας Β, η εσωτερική του ενέργεια θα μεταβληθεί. Σύμφωνα με τη σχέση (2.5) η μεταβολή της εσωτερικής ενέργειας του αερίου εξαρτάται μόνο από την αρχική και τελική θερμοκρασία και όχι από τον τρόπο που πραγματοποιήθηκε η μεταβολή. Γενικότερα η μεταβολή στην εσωτερική ενέργεια ενός θερμοδυναμικού συστήματος εξαρτάται μόνο από την αρχική και την τελική κατάσταση του συστήματος. 
Η μεταβολή της εσωτερικής ενέργειας ενός θερμοδυναμικού συστήματος εξαρτάται μόνο από την αρχική και την τελική κατάσταση του συστήματος και όχι από τον τρόπο που πραγματοποιήθηκε η μεταβολή. 2-8 ΠΡΩΤΟΣ ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ
Ένα αέριο μεταβαίνει από μια αρχική κατάσταση σε μια άλλη. Έστω ότι κατά τη διάρκεια αυτής της μεταβολής το αέριο απορρόφησε ποσό θερμότητας Q και ότι το έργο που παράγει το αέριο κατά τη μεταβολή αυτή είναι W. Η θερμότητα που προσφέρθηκε στο αέριο μετασχηματίζεται σε ενέργεια άλλης μορφής. Συγκεκριμένα, ένα μέρος της μπορεί να χρησιμοποιηθεί για να αυξήσει την εσωτερική ενέργεια του αερίου και το υπόλοιπο μετατρέπεται σε μηχανικό έργο. Το ποσό της θερμότητας που προσφέρεται στο αέριο, η μεταβολή της εσωτερικής ενέργειας του αερίου και το έργο που παράγει το αέριο συνδέονται μεταξύ τους με τη σχέση
|
Η σχέση (2.6) αποτελεί τον πρώτο θερμοδυναμικό νόμο.
Το ποσό θερμότητας (Q) που απορροφά ή αποβάλλει ένα θερμοδυναμικό σύστημα είναι ίσο με το αλγεβρικό άθροισμα τηςμεταβολής της εσωτερικής του ενέργειας και του έργου που παράγει ή δαπανά το σύστημα.
Ο πρώτος θερμοδυναμικός νόμος είναι η εφαρμογή της αρχής διατήρησης της ενέργειας στη θερμοδυναμική.
Το παράδειγμα που ακολουθεί αποτελεί ένα μηχανικό ισοδύναμο του πρώτου θερμοδυναμικού νόμου.

Αν το σύστημα απορροφά θερμότητα, το Q στην σχέση (2.6) είναι θετικό, αν αποβάλλει θερμότητα είναι αρνητικό. Η μεταβολή της εσωτερικής ενέργειας είναι θετική όταν αυξάνει η θερμοκρασία του συστήματος και αρνητική όταν μειώνεται. Το έργο του αερίου είναι θετικό όταν το αέριο εκτονώνεται και αρνητικό όταν συμπιέζεται.
2-9 ΕΦΑΡΜΟΓΗ ΤΟΥ ΠΡΩΤΟΥ ΘΕΡΜΟΔΥΝΑΜΙΚΟΥ ΝΟΜΟΥ
ΣΕ ΕΙΔΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ Α) Ισόθερμη αντιστρεπτή μεταβολή
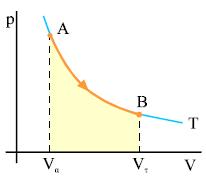
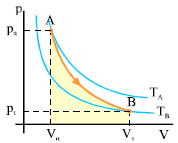
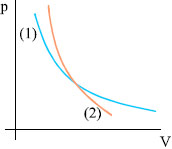
Έστω μια ισόθερμη αντιστρεπτή μεταβολή ορισμένης ποσότητας αερίου από την αρχική κατάσταση Α, όγκου Vα, στην τελική κατάσταση Β, όγκου Vτ. Η μεταβολή γίνεται σε σταθερή θερμοκρασία Τ. Το σχήμα 2.11 παριστάνει γραφικά τη μεταβολή. Το εμβαδόν κάτω από την γραμμή του διαγράμματος είναι ίσο με το έργο που παράγει το αέριο. Από τον υπολογισμό του εμβαδού, που δεν είναι δυνατόν να γίνει χωρίς τη χρήση ολοκληρωμάτων, προκύπτει ότι
Επειδή η θερμοκρασία του αερίου δε μεταβάλλεται, UA=UB επομένως ΔU=0, οπότε ο πρώτος θερμοδυναμικός νόμος, στην ισόθερμη μεταβολή, παίρνει τη μορφή
Στην ισόθερμη εκτόνωση όλο το ποσό θερμότητας που απορροφά το αέριο μετατρέπεται σε μηχανικό έργο. |
Σχ. 2.10 Η δεξαμενή τροφοδοτείται από κάποια πηγή και δίνει νερό σε δίκτυο, μέσω αγωγού. Η δεξαμενή παίζει το ρόλο του θερμοδυναμικού συστήματος. Το νερό μέσα στη δεξαμενή αντιστοιχεί στην εσωτερική ενέργεια, το νερό που εισέρχεται στη θερμότητα και το νερό που εξέρχεται στο μηχανικό έργο.
Σχ. 2.10 Η δεξαμενή τροφοδοτείται από κάποια πηγή και δίνει νερό σε δίκτυο, μέσω αγωγού. Η δεξαμενή παίζει το ρόλο του θερμοδυναμικού συστήματος. Το νερό μέσα στη δεξαμενή αντιστοιχεί στην εσωτερική ενέργεια, το νερό που εισέρχεται στη θερμότητα και το νερό που εξέρχεται στο μηχανικό έργο. |
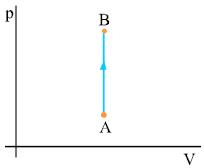 Σχ. 2.12 Η ισόχωρη μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β. Σχ. 2.12 Η ισόχωρη μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β.
 Σχ. 2.13 Η ισόβαρής μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β. Σχ. 2.13 Η ισόβαρής μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β.
 Σχ. 2.14 Τα τοιχώματα του δοχείου καθώς και το έμβολο είναι από μονωτικό υλικό. Στη διάρκεια της μεταβολής το αέριο δεν ανταλλάσσει θερμότητα με το περιβάλλον. Σχ. 2.14 Τα τοιχώματα του δοχείου καθώς και το έμβολο είναι από μονωτικό υλικό. Στη διάρκεια της μεταβολής το αέριο δεν ανταλλάσσει θερμότητα με το περιβάλλον. |
Β) Ισόχωρη αντιστρεπτή μεταβολή
Έστω η ισόχωρη αντιστρεπτή μεταβολή μιας ποσότητας αερίου, από την κατάσταση Α στην κατάσταση Β. Το αέριο θερμαίνεται με σταθερό όγκο και η θερμοκρασία του αυξάνεται. Το σχήμα 2.12 παριστάνει γραφικά τη μεταβολή. Από το σχήμα φαίνεται ότι το έργο του αερίου είναι μηδέν. Αυτό είναι αναμενόμενο γιατί έργο έχουμε μόνο όταν ο όγκος του αερίου μεταβάλλεται.
Στην ισόχωρη θέρμανση όλο το ποσό θερμότητας που απορρόφησε το αέριο χρησιμοποιήθηκε για την αύξηση της εσωτερικής του ενέργειας.
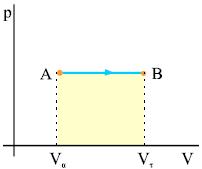
Γ) Ισοβαρής αντιστρεπτή μεταβολή
Ένα αέριο θερμαίνεται ισοβαρώς από την αρχική κατάσταση Α, όγκου Vα , στην τελική κατάσταση Β, όγκου Vτ . Το σχήμα 2.13 παριστάνει γραφικά τη μεταβολή. Το εμβαδόν κάτω από την γραμμή του διαγράμματος δίνει το έργο του αερίου.
Ο πρώτος θερμοδυναμικός νόμος παίρνει τη μορφή
Στην ισοβαρή θέρμανση ένα μέρος από το ποσό θερμότητας που απορρόφησε το αέριο από το περιβάλλον χρησιμοποιήθηκε για την αύξηση της εσωτερικής του ενέργειας και το υπόλοιπο αποδόθηκε εκ νέου στο περιβάλλον με τη μορφή έργου
Δ) Αδιαβατική μεταβολή
Αδιαβατική ονομάζουμε τη μεταβολή κατά την οποία δε συντελείται μεταφορά θερμότητας από το περιβάλλον προς το σύστημα ή αντίστροφα.
Έστω ένα αέριο που εκτονώνεται με αντιστρεπτό τρόπο μέσα σε δοχείο με έμβολο από την κατάσταση Α (pα, Vα) στην κατάσταση Β (pτ, Vτ) (σχ. 2.14). Το δοχείο και το έμβολο είναι κατασκευασμένα έτσι ώστε να μην επιτρέπουν την ανταλλαγή θερμότητας ανάμεσα στο αέριο και στο περιβάλλον (ένα τέτοιο δοχείο είναι το θερμός που χρησιμοποιούμε στα σπίτια μας). Η μεταβολή αυτή είναι μια αντιστρεπτή αδιαβατική μεταβολή.
Ο νόμος που διέπει τη μεταβολή είναι
|
όπου γ ένας καθαρός αριθμός, μεγαλύτερος της μονάδας, που εξαρτάται από την ατομικότητα του αερίου και από το είδος των δεσμών που συγκρατούν τα άτομα στο μόριο. Για τον αριθμό αυτό θα μιλήσουμε στην επόμενη ενότητα.
Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο και λαμβάνοντας υπόψη ότι Q=0 προκύπτει
Επειδή στη μεταβολή που περιγράψαμε το έργο είναι θετικό, από τη σχέση (2.7) προκύπτει ότι η εσωτερική ενέργεια μειώνεται, επομένως το αέριο ψύχεται. Το σχήμα 2.15 παριστάνει την αντιστρεπτή αδιαβατική μεταβολή που περιγράψαμε. Επειδή η τελική θερμοκρασία είναι μικρότερη από την αρχική, η καμπύλη της έχει μεγαλύτερη κλίση από την ισόθερμη που περνάει από το σημείο Α. Στην αδιαβατική μεταβολή το έργο μπορεί να υπολογιστεί από τη σχέση
Ο πρώτος θερμοδυναμικός νόμος είναι η εφαρμογή της αρχής διατήρησης της ενέργειας στη θερμοδυναμική.
Στην πράξη όταν ένα αέριο συμπιέζεται (ή εκτονώνεται) πολύ γρήγορα, πολύ μικρό ποσό θερμότητας μετακινείται από το αέριο προς το περιβάλλον ή αντίστροφα. Η διεργασία αυτή είναι σχεδόν αδιαβατική. Τέτοιες διεργασίες συμβαίνουν στον κύλινδρο του βενζινοκινητήρα. E)Κυκλική αντιστρεπτή μεταβολή
Κυκλική ονομάζουμε μια μεταβολή στην οποία το σύστημα μετά από μια διεργασία επιστρέφει στην ίδια κατάσταση.
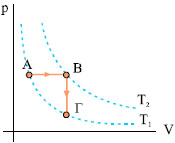
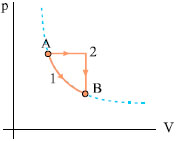
Το σχήμα 2.16 παριστάνει μια κυκλική αντιστρεπτή μεταβολή ορισμένης ποσότητας αερίου. Το αέριο αρχικά βρισκόταν στην κατάσταση Α και μετά από μια διεργασία επιστρέφει πάλι στην αρχική κατάσταση Α.
Το έργο του αερίου μπορεί να υπολογιστεί ως εξής: Το έργο του αερίου κατά τη μεταβολή από το Α στο Β είναι ίσο με το εμβαδόν του τμήματος που είναι σκιασμένο με κόκκινο και είναι θετικό, γιατί το αέριο εκτονώνεται. Το έργο, κατά τη μεταβολή από το Β στο Α, είναι ίσο με το εμβαδόν του τμήματος που είναι σκιασμένο με πράσινο και είναι αρνητικό γιατί το αέριο συμπιέζεται. Το έργο του αερίου σε ολόκληρη την κυκλική μεταβολή που είναι το αλγεβρικό άθροισμα αυτών των έργων, είναι ίσο με το εμβαδόν που περικλείει η κλειστή γραμμή που περιγράφει τη μεταβολή. 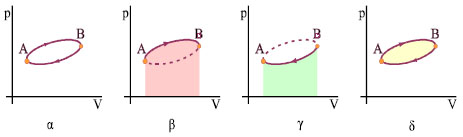
|
 Σχ. 2.15 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Σχ. 2.15 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β.
Σχ. 2.16 Το σχήμα α παριστάνει γραφικά μια αντιστρεπτή κυκλική μεταβολή. Το εμβαδόν της χρωματισμένης επιφάνειας στο σχήμα β δίνει το έργο του αερίου κατά την μεταβολή Α→Β. Το έργο κατά τη μεταβολή Β→Α είναι κατ' απόλυτη τιμή ίσο με το εμβαδόν της χρωματι-σμένης επιφάνειας στο σχήμα γ, η αλγεβρική του τιμή όμως είναι αρνητική. Το συνολικό έργο προκύπτει αν από το εμβαδόν του σχήματος β αφαιρέσουμε το εμβαδόν του σχήματος γ. Από την αφαίρεση αυτή προκύπτει το εμβαδόν που περικλείει η γραμμή του διαγράμματος (σχ. δ). |
|
Το ολικό έργο σε μια κυκλική αντιστρεπτή μεταβολή είναι ίσο με το εμβαδόν που περικλείεται από τη γραμμή του διαγράμματος, στη γραφική παράσταση p-V.
Εάν η κυκλική μεταβολή διαγραφόταν κατά την αντίθετη φορά, για να υπολογίσουμε το έργο θα αφαιρούσαμε από το μικρό εμβαδόν το μεγάλο. Έτσι, το συνολικό έργο θα ήταν αρνητικό. Επομένως σε μια αντιστρεπτή κυκλική μεταβολή, το έργο είναι θετικό όταν η γραφική παράσταση της μεταβολής διαγράφεται με την φορά των δεικτών του ρολογιού και αρνητικό όταν διαγράφεται με την αντίθετη φορά. Επειδή το αέριο επιστρέφει στην αρχική του κατάσταση, η μεταβολή στην εσωτερική του ενέργεια είναι μηδέν ΔU = 0. Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο στην κυκλική μεταβολή έχουμε
Στην κυκλική μεταβολή η θερμότητα που απορροφά ή αποδίδει το αέριο ισούται με το έργο που παράγει ή δαπανά.
2-10 ΓΡΑΜΜΟΜΟΡΙΑΚΕΣ ΕΙΔΙΚΕΣ ΘΕΡΜΟΤΗΤΕΣ
ΑΕΡΙΩΝ Έχει βρεθεί πειραματικά ότι το ποσό θερμότητας που απαιτείται για να αυξηθεί η θερμοκρασία ενός σώματος μάζας m, κατά ΔΤ δίνεται από τη σχέση
όπου c είναι η ειδική θερμότητα του υλικού. Στα υγρά και στα στερεά η ειδική θερμότητα του σώματος εξαρτάται μόνο από το υλικό του.
Αν αντί για τη μάζα του σώματος χρησιμοποιήσουμε την ποσότητά του σε mol, επειδή m = n M, όπου Μ η γραμμομοριακή μάζα, μπορούμε να γράψουμε τη σχέση (2.8) με τη μορφή
Το γινόμενο Μ c ονομάζεται γραμμομοριακή ειδική θερμότητα και συμβολίζεται με C. Αντικαθιστώντας το γινόμενο Μ c με το C η σχέση (2.9) γίνεται
Η γραμμομοριακή ειδική θερμότητα C, στο SI, μετριέται σε J/(mol K) και εκφράζει το ποσό θερμότητας που πρέπει να προσφερθεί σε 1 mol του σώματος για να αυξηθεί η θερμοκρασία του κατά ένα βαθμό.
Ενώ η ειδική θερμότητα στα υγρά και στα στερεά εξαρτάται μόνο από το υλικό, στα αέρια η γραμμομοριακή ειδική θερμότητα εξαρτάται και από τον τρόπο με τον οποίο θερμαίνεται το αέριο. Από όλους του δυνατούς τρόπους με τους οποίους μπορεί να θερμανθεί ένα αέριο, και τις αντίστοιχες γραμμομοριακές ειδικές θερμότητες που προκύπτουν, ιδιαίτερο ενδιαφέρον παρουσιάζουν δύο, η θέρμανση με σταθερό όγκο και η θέρμανση με σταθερή πίεση. |
Θέρμανση αερίου με σταθερό όγκο
Το αέριο του σχήματος 2.17 βρίσκεται μέσα σε δοχείο σταθερού όγκου και θερμαίνεται ώστε η θερμοκρασία του να αυξηθεί κατά ΔΤ. Αν συμβολίσουμε με Qv το ποσό θερμότητας που απορροφά το αέριο και με Cv τη γραμμομοριακή ειδική θερμότητα κατά την ισόχωρη αυτή θέρμανση έχουμε
Αφού ο όγκος του αερίου δε μεταβάλλεται το έργο του αερίου είναι μηδέν. Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο έχουμε
Η σχέση (2.11), λόγω της (2.10), γίνεται
Πρέπει να τονιστεί ότι επειδή η εσωτερική ενέργεια ενός αερίου εξαρτάται μόνο από την αρχική και τελική θερμοκρασία του αερίου η σχέση (2.12) δίνει τη μεταβολή της εσωτερικής ενέργειας σε κάθε περίπτωση που η θερμοκρασία ενός αερίου μεταβάλλεται κατά ΔΤ, με όποιον τρόπο και αν πραγματοποιείται αυτή η μεταβολή.
Θέρμανση αερίου με σταθερή πίεση
Έστω ότι η ίδια ποσότητα αερίου θερμαίνεται ισοβαρώς (σχ. 2.18) ώστε η θερμοκρασία του να μεταβληθεί κατά το ίδιο ποσό ΔΤ. Αν συμβολίσουμε με Qp και Cp τη θερμότητα και τη γραμμομοριακή ειδική θερμότητα του αερίου στην ισοβαρή θέρμανση, μπορούμε να γράψουμε
Το έργο που παράγει το αέριο είναι W = p ΔV. Από την καταστατική εξίσωση έχουμε p ΔV = n R ΔΤ, οπότε η σχέση που δίνει το έργο γίνεται
Από τον πρώτο θερμοδυναμικό νόμο Q = ΔU + W, αν λάβουμε υπόψη τις (2.12) και (2.13), προκύπτει
ή
Η σχέση 2.14 δείχνει ότι η Cp είναι μεγαλύτερη από τη Cv κατά την ποσότητα R.
|
 Σχ. 2.17 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Σχ. 2.17 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β.
 Σχ. 2.18 Θέρμανση αερίου με σταθερή πίεση. Σχ. 2.18 Θέρμανση αερίου με σταθερή πίεση.
|
|
Υπολογισμός των Cp και Cv
Όταν η θερμοκρασία του αερίου μεταβάλλεται κατά ΔΤ η εσωτερική του ενέργεια
Η ποσότητα γ που συναντήσαμε στο νόμο της αδιαβατικής μεταβολής είναι ο λόγος των δύο γραμμομοριακών ειδικών θερμοτήτων.
το γ είναι καθαρός αριθμός μεγαλύτερος της μονάδας και στα ιδανικά αέρια σύμφωνα με τις σχέσεις (2.15) και (2.16) έχει την τιμή γ = 5/3.
και το είδος των δεσμών που συγκρατούν τα άτομα στο μόριο. Ο πίνακας που ακολουθεί δίνει τις γραμμομοριακές ειδικές θερμότητες ορισμένων αερίων όπως μετρήθηκαν πειραματικά.
|
Παρατηρούμε ότι η θεωρητική πρόβλεψη για τα Cv και Cp με βάση το ιδανικό αέριο, συμφωνεί απόλυτα με τα πειραματικά δεδομένα αν πρόκειται για μονοατομικό αέριο, ενώ αποκλίνει αισθητά για τα διατομικά και πολυατομικά αέρια. Αυτό οφείλεται στο γεγονός ότι ενώ τα μόρια των μονοατομικών αερίων προσεγγίζουν το μοντέλο του ιδανικού αερίου τα μόρια που αποτελούνται από περισσότερα άτομα εμφανίζουν δομή που δεν γίνεται να αγνοηθεί. Πιο συγκεκριμένα, στο ιδανικό αέριο θεωρήσαμε τα μόρια υλικά σημεία, οπότε η μόνη δυνατότητα κίνησης είναι η μεταφορική κίνηση και υπολογίσαμε την εσωτερική του ενέργεια ως το άθροισμα των μεταφορικών κινητικών ενεργειών των μορίων του. Τα διατομικά μόρια, όπως τα μόρια του Ν2 και του Ο2 πρέπει να θεωρηθούν ότι αποτελούνται από δύο σωματίδια συνδεδεμένα μεταξύ τους. Εκτός από τη δυνατότητα που έχει ένα τέτοιο μόριο να κάνει μεταφορική κίνηση, τα σωματίδια που το αποτελούν έχουν τη δυνατότητα να περιστρέφονται γύρω από το κοινό κέντρο μάζας τους και, κάτω από ορισμένες συνθήκες (υψηλή θερμοκρασία), να ταλαντώνονται. Όλες αυτές οι κινήσεις συνεισφέρουν στην εσωτερική ενέργεια. Έτσι, αν θέλαμε να κάνουμε πιο ακριβείς υπολογισμούς όταν υπολογίζουμε την εσωτερική ενέργεια θα πρέπει για τέτοια αέρια (διατομικά-τριατομικά) να λάβουμε υπόψη όλες τις κινήσεις. Όμως, όπως φαίνεται στον πίνακα, ακόμα και σ΄ αυτές τις περιπτώσεις (διατομικά ή πολυατομικά μόρια) η διαφορά Cp-Cv συμφωνεί, με μεγάλη προσέγγιση, με τη σχέση 2.14.
2-11 ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ
Θερμικές μηχανές ονομάζουμε τις διατάξεις που μετατρέπουν τη θερμότητα σε μηχανικό έργο.
Η ιστορία των μηχανών αυτών αρχίζει το 1712 όταν ο Thomas Newcomen (Τόμας Νιουκάμεν) επινόησε την πρώτη ατμομηχανή. Η ατμομηχανή του Newcomen ήταν αρκετά χοντροκομμένη και χρησιμοποιήθηκε για την άντληση νερού από τα ορυχεία. Το 1769 ο Watt, βελτίωσε την μηχανή του Newcomen και παρουσίασε μια μηχανή για πολλές χρήσεις. Η εφεύρεση της ατμομηχανής και στη συνέχεια η διάδοση της χρήσης της είχε ως αποτέλεσμα βαθιές αλλαγές στη ζωή των ανθρώπων και στις κοινωνικές δομές. Η περίοδος που ακολούθησε ονομάστηκε βιομηχανική επανάσταση. Από την εποχή του Newcomen και του Watt μέχρι σήμερα οι θερμικές μηχανές έκαναν μεγάλο δρόμο. Οι ατμομηχανές τελειοποιήθηκαν, επινοήθηκαν νέες θερμικές μηχανές, όπως οι μηχανές ντίζελ, οι βενζινοκινητήρες, οι αεροστρόβιλοι που χρησιμοποιούνται στα αεροπλάνα και οι ατμοστρόβιλοι που χρησιμοποιούνται στα εργοστάσια παραγωγής ηλεκτρικής ενέργειας. Το μεγαλύτερο μέρος της ενέργειας που χρησιμοποιούμε σήμερα σχετίζεται με τη χρήση των θερμικών μηχανών.
Το σχήμα 2.19 παριστάνει το μοντέλο μιας ατμομηχανής. Στο λέβητα παράγεται θερμός ατμός υψηλής πίεσης, ο οποίος - μέσω της βαλβίδας Α (βαλβίδα εισαγωγής) - διοχετεύεται στον κύλινδρο, σπρώχνει το έμβολο και παράγει έργο. Καθώς ο ατμός εκτονώνεται μέσα στον κύλινδρο, η πίεση και η
|
 Εικ. 2.3 H ατμομηχανή του Watt. Εικ. 2.3 H ατμομηχανή του Watt. |
Σχ. 2.19 Αρχή λειτουργίας της ατμομηχανής.
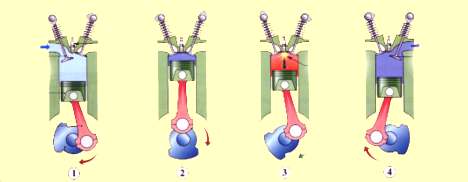
Σχ. 2.4 Κύκλος βενζινοκινητήρα τεσσάρων χρόνων. (1) Το έμβολο κατεβαίνει. Η βαλβίδα εισόδου είναι ανοικτή, μίγμα βενζίνης - αέρα γεμίζει τον κύλινδρο.(2) Το έμβολο ανεβαίνει. Οι βαλβίδες είναι κλειστές και το μίγμα συμπιέζεται (3) Το μίγμα αναφλέγεται με το σπινθήρα που προκαλεί το μπουζί και τα αέρια της καύσης απωθούν βίαια το έμβολο προς τα κάτω (4) Το έμβολο ανεβαίνει. Η βαλβίδα εξαγωγής είναι ανοικτή και τα καυσαέρια απομακρύνονται από τον κύλινδρο.
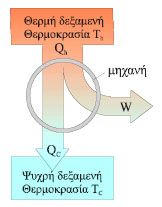 Σχ. 2.20 Αρχή λειτουργίας μιας θερμικής μηχανής. Η κυκλική περι-οχή συμβολίζει τη μηχανή η οποία δέχεται ποσό θερμότητας Qh από τη θερμή δεξαμενή, παράγει έργο W και αποβάλλει ποσό θερμότητας Qc στην ψυχρή δεξαμενή. Σχ. 2.20 Αρχή λειτουργίας μιας θερμικής μηχανής. Η κυκλική περι-οχή συμβολίζει τη μηχανή η οποία δέχεται ποσό θερμότητας Qh από τη θερμή δεξαμενή, παράγει έργο W και αποβάλλει ποσό θερμότητας Qc στην ψυχρή δεξαμενή. |
θερμοκρασία του ελαττώνονται. Στη συνέχεια ο ατμός που τώρα έχει χαμηλή πίεση αποβάλλεται από τον κύλινδρο, από τη βαλβίδα Β (βαλβίδα εξαγωγής), και διοχετεύεται σε μια διάταξη που ονομάζεται συμπυκνωτής. Εκεί ο ατμός ψύχεται με τρεχούμενο νερό ή από τον αέρα και συμπυκνώνεται πάλι σε νερό. Το νερό οδηγείται πίσω στο λέβητα.
Στους βενζινοκινητήρες, τα θερμά αέρια που παράγονται από την καύση της βενζίνης με τον αέρα σπρώχνουν το έμβολο του κυλίνδρου και παράγουν έργο. Στη συνέχεια αποβάλλονται από τον κύλινδρο και μέσω της εξάτμισης διοχετεύονται στο περιβάλλον.
Σχηματικά θα μπορούσαμε να πούμε ότι η θερμική μηχανή είναι μια διάταξη που υποβάλλει ένα «μέσον» σε μια μεταβολή. Επειδή η μηχανή μετατρέπει συνεχώς τη θερμότητα σε έργο πρέπει η μεταβολή στην οποία υποβάλλεται το μέσον να είναι κυκλική, ώστε, όταν ολοκληρωθεί η μεταβολή, η μηχανή να επιστρέψει στην αρχική της κατάσταση και να επαναλάβει την ίδια διαδικασία ξανά και ξανά. Στην ατμομηχανή το υλικό που υποβάλλεται στην κυκλική διεργασία είναι το νερό. Το νερό αφού γίνει ατμός και ολοκληρώσει την πορεία του μέσω του κυλίνδρου και του συμπυκνωτή επιστρέφει στο λέβητα στις ίδιες συνθήκες.
Κατά τη διάρκεια της κυκλικής μεταβολής του μέσου, η μηχανή
|
Προηγουμένως χρησιμοποιήσαμε τον όρο δεξαμενή θερμότητας. Έτσι συνηθίζουμε να λέμε ένα σώμα που παραμένει σε σταθερή θερμοκρασία ακόμη κι αν παίρνει ή δίνει θερμότητα. Στην ατμομηχανή δεξαμενή υψηλής θερμοκρασίας είναι ο λέβητας, του οποίου η θερμοκρασία διατηρείται σταθερή μέσω της ελεγχόμενης καύσης κάποιου καυσίμου, ενώ δεξαμενή χαμηλής θερμοκρασίας είναι ο συμπυκνωτής, ο οποίος βρίσκεται σε επαφή ή με την ατμόσφαιρα ή με μια μάζα νερού, οπότε η θερμοκρασία του διατηρείται επίσης σταθερή. Στις μηχανές εσωτερικής καύσης το καιόμενο υγρό καύσιμο μέσα στο θάλαμο καύσης -κύλινδρο- είναι η δεξαμενή υψηλής θερμοκρασίας και το περιβάλλον, όπου διοχετεύονται τα καυσαέρια, η δεξαμενή χαμηλής θερμοκρασίας.
O συντελεστής απόδοσης (e) οποιασδήποτε μηχανής είναι ο λόγος τουωφέλιμου έργου που μας δίνει η μηχανή προς την ενέργεια που δαπανούμεγια να λειτουργήσει.
Στη θερμική μηχανή η ενέργεια που δαπανούμε είναι η θερμότητα Qh με την οποία τροφοδοτούμε τη μηχανή από τη δεξαμενή υψηλής θερμοκρασίας.
Το καθαρό ποσό θερμότητας Q που απορροφά το μέσον είναι το ποσό θερμότητας που παίρνει από τη δεξαμενή υψηλής θερμοκρασίας μείον αυτό που αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας, Qh - |Qc|. Στην κυκλική μεταβολή το έργο που παράγει το αέριο ισούται με το καθαρό ποσό θερμότητας που απορροφά δηλαδή Αντικαθιστώντας στη (2.17) βρίσκουμε
Από την εποχή του Newcomen και του Watt μέχρι σήμερα οι θερμικές μηχανές έκαναν μεγάλο δρόμο. Οι ατμομηχανές τελειοποιήθηκαν, επινοήθηκαν νέες θερμικές μηχανές, όπως οι μηχανές ντίζελ, οι βενζινοκινητήρες, οι αεροστρόβιλοι που χρησιμοποιούνται στα αεροπλάνα και οι ατμοστρόβιλοι που χρησιμοποιούνται στα εργοστάσια παραγωγής ηλεκτρικής ενέργειας. Το μεγαλύτερο μέρος της ενέργειας που χρησιμοποιούμε σήμερα σχετίζεται με τη χρήση των θερμικών μηχανών.
Το σχήμα 2.19 παριστάνει το μοντέλο μιας ατμομηχανής. Στο λέβητα παράγεται θερμός ατμός υψηλής πίεσης, ο οποίος - μέσω της βαλβίδας Α (βαλβίδα εισαγωγής) - διοχετεύεται στον κύλινδρο, σπρώχνει το έμβολο και παράγει έργο. Καθώς ο ατμός εκτονώνεται μέσα στον κύλινδρο, η πίεση και η
|
 Εικ. 2.5 Βενζινοκινητήρας Εικ. 2.5 Βενζινοκινητήραςαυτοκινήτου. |
ΠΑΡΑΔΕΙΓΜΑ 2.1 |
|||||||||
Μηχανή εσωτερικής καύσης καταναλώνει σε κάθε κύκλο λειτουργίας της θερμότητα 5000 J και αποβάλλει στην εξάτμιση θερμότητα 3500 J. Υπολογίστε το συντελεστή απόδοσης της μηχανής. Απάντηση:Ο συντελεστής απόδοσης μιας μηχανής δίνεται από την σχέση (2.18)
|
 Εικ. 2.6 Ατμοστρόβιλος σε εργοστάσιο παραγωγής ηλεκτρικής ενέργειας. Εικ. 2.6 Ατμοστρόβιλος σε εργοστάσιο παραγωγής ηλεκτρικής ενέργειας.
|
 Εικ. 2.7 Πυρηνικό εργοστάσιο παραγωγής ηλεκτρικής ενέργειας στη Βιρτζίνια των Η.Π.Α. Παράγει ηλεκτρική ισχύ 900 ΜW και ταυτόχρονα αποβάλλει στο κοντινό ποτάμι θερμότητα με ρυθμό 2100 ΜW. To εργοστάσιο αυτό όπως και τα υπόλοιπα του είδους του «πετάει» πολύ περισσότερη ενέργεια από όση αποδίδει σε χρήσιμη μορφή. Εικ. 2.7 Πυρηνικό εργοστάσιο παραγωγής ηλεκτρικής ενέργειας στη Βιρτζίνια των Η.Π.Α. Παράγει ηλεκτρική ισχύ 900 ΜW και ταυτόχρονα αποβάλλει στο κοντινό ποτάμι θερμότητα με ρυθμό 2100 ΜW. To εργοστάσιο αυτό όπως και τα υπόλοιπα του είδους του «πετάει» πολύ περισσότερη ενέργεια από όση αποδίδει σε χρήσιμη μορφή. |
ΠΑΡΑΔΕΙΓΜΑ 2.2 |
||||||||||||||
Θερμική μηχανή έχει απόδοση 25%, και σε κάθε κύκλο παράγει ωφέλιμο έργο 2000 J. Υπολογίστε την ενέργεια που δαπανάται για κάθε κύκλο λειτουργίας της μηχανής. Απάντηση:Ο συντελεστής απόδοσης μιας μηχανής δίνεται από τη σχέση (2.17)
Για τη λειτουργία της μηχανής δαπανάται θερμότητα 8000 J σε κάθε κύκλο. ΠΑΡΑΔΕΙΓΜΑ 2.3 |
Ο κινητήρας Diesel της εικόνας χρησιμοποιείται σε μικρά φορτηγά πλοία. Ο συντελεστής απόδοσης ενός τέτοιου κινητήρα είναι 0,25. Το πλοίο που τον φέρει ταξιδεύει με 15 κόμβους. Οι δεξαμενές του πλοίου περιέχουν 150 τόνους καυσίμου. Ποια απόσταση μπορεί να διανύσει το πλοίο με αυτά τα καύσιμα; [1 κόμβος = 1 ναυτικό μίλι /h = 1852 m/h. 1 kg καυσίμου αποδίδει κατά την καύση του 39800 kJ].
Απάντηση: Ο κινητήρας αποδίδει ισχύ P = 12 x 220kW = 2640kW Η απόδοση του κινητήρα είναι ο λόγος της μηχανικής ισχύος (P) που αποδίδει ο κινητήρας κατά τη λειτουργία του προς την θερμική ισχύ (Ph) που παίρνει κατά την καύση του καυσίμου.
|
 Εικ. 2.8 Φινλανδικός κινητήρας Diesel Wartsila Εικ. 2.8 Φινλανδικός κινητήρας Diesel Wartsila 12 κύλινδροι σε διάταξη V. Εσωτερική διάμετρος κυλίνδρου: 200 mm. Διαδρομή εμβόλου: 240 mm. Κυλινδρισμός: 7,54 L ανά κύλινδρο. Ισχύς: 220 kW ανά κύλινδρο για ταχύτητα 15 κόμβων. |
Από τα καύσιμα, σε χρονικό διάστημα Δt = 1 h αποδίδεται θερμότητα
Qh = PhΔt = 10.560kW·3.600 s = 38.016.000kJ
Η μάζα του καυσίμου που αποδίδει τόση θερμότητα κατά την καύση της είναι
Σε μια ώρα το πλοίο διανύει 15ν.μ / h x 1852m / ν.μ x 1h = 27780m = 27,78
Αφού με 955 kg καυσίμου το πλοίο διανύει 27,78 km με τους 150 τόνους θα διανύσει
ΠΑΡΑΔΕΙΓΜΑ 2.3
|
Kύκλος Otto (βενζινοκινητήρας) Το ιδανικό αέριο θερμικής μηχανής εκτελεί την κυκλική μεταβολή του σχήματος 2.21 που περιλαμβάνει τις πιο κάτω διαδοχικές μεταβολές. |
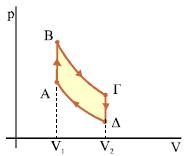 Σχ. 2.21 Σχ. 2.21 |
Απάντηση:
 |
||||||||||||||||||||||||||||||||
2-12 Ο ΔΕΥΤΕΡΟΣ ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ
Η θερμοδυναμική έκανε τα πρώτα της βήματα στις αρχές του 19ου αιώνα, προσπαθώντας να δώσει λύση στα πρακτικά προβλήματα που επέβαλε η χρήση των θερμικών μηχανών. Όπως φαίνεται και από τη σχέση (2.18), ο συντελεστής απόδοσης μιας θερμικής μηχανής είναι μικρότερος από ένα. Θα ήταν ένα αν η μηχανή μετέτρεπε όλο το ποσό της θερμότητας σε ωφέλιμο έργο, ωστόσο κανένας δεν κατόρθωσε να κατασκευάσει μια τέτοια μηχανή. Όλες οι μηχανές εκμεταλλεύονται μόνο ένα μέρος της θερμότητας και αποβάλλουν σημαντικά ποσά θερμότητας στο περιβάλλον. Οι επανειλημμένες αποτυχίες των ερευνητών να κατασκευάσουν την “τέλεια” θερμική μηχανή που θα μετέτρεπε πλήρως τη θερμότητα σε ωφέλιμο έργο έπεισαν ότι η αδυναμία οφείλεται σε περιορισμούς που θέτει η ίδια η φύση. Η διαπίστωση αυτή οδήγησε στη διατύπωση του δεύτερου θερμοδυναμικού νόμου, από τους Kelvin και Planck (Κέλβιν και Πλανκ):
Είναι αδύνατο να κατασκευαστεί θερμική μηχανή που να μετατρέπει εξ ολοκλήρου τη θερμότητα σε ωφέλιμο έργο.
Μιλώντας για τη θερμότητα, είπαμε ότι, από μόνη της, μεταφέρεται πάντα από τα θερμότερα προς τα ψυχρότερα σώματα. Η αντίστροφη πορεία απαιτεί δαπάνη ενέργειας. Το ψυγείο και το κλιματιστικό είναι μηχανήματα που αναγκάζουν τη θερμότητα να μεταφερθεί από ψυχρά σώματα σε θερμότερα. Το ψυγείο, για παράδειγμα, μεταφέρει θερμότητα από τα τρόφιμα στο περιβάλλον, που είναι θερμότερο. Όμως για τη λειτουργία αυτών των μηχανών δαπανούμε ενέργεια. Δεν είναι δυνατόν να κατασκευαστεί ψυγείο που να λειτουργεί χωρίς να δαπανάται ενέργεια. Αυτή η διαπίστωση οδήγησε σε μια άλλη διατύπωση του δεύτερου θερμοδυναμικού νόμου από τον Clausious (Κλαούζιους):
Είναι αδύνατο να κατασκευαστεί μηχανή που να μεταφέρει θερμότητα από ένα ψυχρό σώμα σε ένα θερμότερο χωρίς να δαπανάται ενέργεια για τη λειτουργία της.
Οι δύο διατυπώσεις του δεύτερου θερμοδυναμικού νόμου που φαινομενικά είναι εντελώς ασύνδετες, είναι ισοδύναμες. Αν αληθεύει η μία από αυτές θα αληθεύει και η άλλη.
Ο πρώτος θερμοδυναμικός νόμος δεν θέτει περιορισμούς στις μετατροπές της ενέργειας. Σύμφωνα με το δεύτερο, όμως, η φύση θέτει περιορισμούς στη μετατροπή ενέργειας από τη μια μορφή στην άλλη. Η θερμότητα δε μπορεί να μετασχηματιστεί κατά 100% σε μηχανική ενέργεια. Επίσης ο δεύτερος θερμοδυναμικός νόμος, καθορίζοντας ότι η θερμότητα μεταφέρεται πάντα από τα θερμότερα προς τα ψυχρότερα σώματα, καθορίζει την κατεύθυνση προς την οποία τα φαινόμενα συμβαίνουν αυθόρμητα στη φύση.
2-13 H MHXANH TOY CARNOT
Σύμφωνα με το δεύτερο θερμοδυναμικό νόμο, μια θερμική μηχανή δε μπορεί να έχει απόδοση 100%. Ποιος είναι όμως ο μεγαλύτερος συντελεστής απόδοσης που μπορεί να έχει μια μηχανή, όταν δίνονται οι θερμοκρασίες Τh |
 Εικ. 2.10 Λόρδος Κέλβιν (Ουίλιαμ Τόμσον) (1825-1907). Αγγλία. Από οικογένεια εύπορη αλλά ταπεινής καταγωγής ο νεαρός Ουίλιαμ ήταν ένα παιδί θαύμα. Σε ηλικία 22 ετών κατείχε την έδρα της Φυσικής Φιλοσοφίας στο πανεπιστήμιο της Γλασκόβης. Ασχολήθηκε σχεδόν με τα πάντα, με πολλούς κλάδους της φυσικής, με επιχειρήσεις (εγκατέστησε το πρώτο τηλεγραφικό καλώδιο μεταξύ Αμερικής - Ευρώπης) και με την πολιτική (πήρε τίτλο ευγενείας και ήταν μέλος της Βουλής των Λόρδων). Μια από τις δεσπόζουσες προσωπικότητες της επιστήμης στο 19ο αιώνα, σε μια εποχή που η Αγγλία κρατούσε τα σκήπτρα της επιστημονικής πρωτοπορίας Εικ. 2.10 Λόρδος Κέλβιν (Ουίλιαμ Τόμσον) (1825-1907). Αγγλία. Από οικογένεια εύπορη αλλά ταπεινής καταγωγής ο νεαρός Ουίλιαμ ήταν ένα παιδί θαύμα. Σε ηλικία 22 ετών κατείχε την έδρα της Φυσικής Φιλοσοφίας στο πανεπιστήμιο της Γλασκόβης. Ασχολήθηκε σχεδόν με τα πάντα, με πολλούς κλάδους της φυσικής, με επιχειρήσεις (εγκατέστησε το πρώτο τηλεγραφικό καλώδιο μεταξύ Αμερικής - Ευρώπης) και με την πολιτική (πήρε τίτλο ευγενείας και ήταν μέλος της Βουλής των Λόρδων). Μια από τις δεσπόζουσες προσωπικότητες της επιστήμης στο 19ο αιώνα, σε μια εποχή που η Αγγλία κρατούσε τα σκήπτρα της επιστημονικής πρωτοπορίας |
 Εικ. 2.11 Σαντί Καρνό (1796-1832). Γαλλία.Στρατιωτικός και μηχανικός. Απόφοιτος της περίφημης Ecole Polytechnique που ίδρυσε ο Ναπολέων για να αντιπαρατεθεί στην ανω-τερότητα των Άγγλων στις επιστήμες. Εικ. 2.11 Σαντί Καρνό (1796-1832). Γαλλία.Στρατιωτικός και μηχανικός. Απόφοιτος της περίφημης Ecole Polytechnique που ίδρυσε ο Ναπολέων για να αντιπαρατεθεί στην ανω-τερότητα των Άγγλων στις επιστήμες.
Σχ. 2.22 Οι τέσσερις φάσεις του κύκλου Carnot. Το αέριο βρίσκεται σε δοχείο που κλείνεται με έμβολο. Το έμβολο και τα πλευρικά τοιχώματα είναι αδιαβατικά ενώ η βάση του δοχείου διαθερμική
|
και Τc, των δεξαμενών θερμότητας της μηχανής; Το ερώτημα αυτό απαντήθηκε το 1824 από το Γάλλο μηχανικό Carnot (Καρνό). Ο Carnot περιέγραψε μια κυκλική αντιστρεπτή μεταβολή, που ονομάστηκε κύκλος Carnot, και απέδειξε ότι μια θερμική μηχανή που θα ακολουθούσε αυτόν τον αντιστρεπτό κύκλο θα είχε τη μεγαλύτερη δυνατή απόδοση. Μια τέτοια, υποθετική, εξιδανικευμένη μηχανή ονομάζεται μηχανή Carnot και η απόδοσή της αποτελεί το ανώτερο όριο για την απόδοση όλων των άλλων μηχανών. Το συμπέρασμα αυτό είναι γνωστό ως θεώρημα Carnot:
Δεν μπορεί να υπάρξει θερμική μηχανή που να έχει μεγαλύτερη απόδοση από μια μηχανή Carnot η οποία λειτουργεί ανάμεσα στις ίδιες θερμοκρασίες.
Ο κύκλος Carnot αποτελείται από τέσσερις μεταβολές, δύο ισόθερμες και δύο αδιαβατικές. Θα περιγράψουμε τον κύκλο Carnot για ιδανικό αέριο που βρίσκεται μέσα σε κύλινδρο, που φράσσεται με έμβολο.

|
Ο συντελεστής απόδοσης μιας θερμικής μηχανής είναι
Αποδεικνύεται ότι για τον κύκλο Carnot ισχύει
Αντικαθιστώντας τη (2.24) στη (2.23) βρίσκουμε ότι ο συντελεστής απόδοσης της μηχανής Carnot είναι
Το αποτέλεσμα δηλώνει, ότι ο συντελεστής απόδοσης μια μηχανής Carnot εξαρτάται μόνο από τις θερμοκρασίες των δύο δεξαμενών θερμότητας. Η απόδοση είναι μεγάλη όταν η διαφορά θερμοκρασίας είναι μεγάλη και είναι πολύ μικρή όταν οι θερμοκρασίες διαφέρουν λίγο. Επειδή οι περισσότερες πρακτικές εφαρμογές έχουν σαν ψυχρή δεξαμενή το περιβάλλον, δηλαδή θερμοκρασία περίπου 300 Κ, όσο μεγαλύτερη θερμοκρασία έχει το σώμα που "δίνει" θερμότητα τόσο πιο αποδοτική μπορεί να είναι η εκμετάλλευσή της. Επίσης το αποτέλεσμα επιβεβαιώνει το δεύτερο θερμοδυναμικό νόμο. Για να έχουμε απόδοση 100% πρέπει Τc=0, που είναι αδύνατον. |
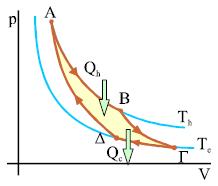 Σχ. 2.23 Διάγραμμα p-V για τον κύκλο Carnot. Το παραγόμενο έργο W, ισούται με την θερμότητα, Qh-|Qc|, που απορροφά το μέσον σε ένα κύκλο. Σχ. 2.23 Διάγραμμα p-V για τον κύκλο Carnot. Το παραγόμενο έργο W, ισούται με την θερμότητα, Qh-|Qc|, που απορροφά το μέσον σε ένα κύκλο.
|
ΠΑΡΑΔΕΙΓΜΑ 2.5 |
|||||||||||||||||||||||
Μηχανή Carnot λειτουργεί ανάμεσα στις θερμοκρασίες Th=500 K και Τc=300 K. Σε κάθε κύκλο αποδίδει έργο W=2000J. Υπολογίστε την απόδοση της μηχανής και την ενέργεια που δαπανάται σε κάθε κύκλο. Απάντηση: Η απόδοση της μηχανής θα υπολογιστεί από τη σχέση (2.25)
Η θερμότητα που δαπανάται για κάθε κύκλο λειτουργίας της μηχανής θα υπολογιστεί από τη σχέση (2.17)
|
 Εικ. 2.12 Ρούντολφ Κλαούζιους (1822-1888). Γερμανία. Ένας από τους θεμελιωτές της θερμοδυναμικής. Εικ. 2.12 Ρούντολφ Κλαούζιους (1822-1888). Γερμανία. Ένας από τους θεμελιωτές της θερμοδυναμικής.
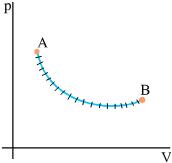 Σχ. 2.24 Σε μια αντιστρεπτή μετα-βολή, η μεταβολή της εντροπίας υπολογίζεται αν χωρίσουμε τη μεταβολή σε πολύ μικρές μεταβολές και αθροίσουμε τις μεταβολές της εντροπίας σε κάθε απειροστή μεταβολή. Σχ. 2.24 Σε μια αντιστρεπτή μετα-βολή, η μεταβολή της εντροπίας υπολογίζεται αν χωρίσουμε τη μεταβολή σε πολύ μικρές μεταβολές και αθροίσουμε τις μεταβολές της εντροπίας σε κάθε απειροστή μεταβολή. Σχ. 2.25 Στα διαγράμματα (α) και (β) ένα θερμοδυναμικό σύστημα μεταβαίνει από την κατάσταση Α στην κατάσταση Β με διαφορετικό κάθε φορά αντιστρεπτό τρόπο. Στο (γ) το ίδιο σύστημα μεταβαίνει από την κατάσταση Α στη Β με μη αντιστρεπτό τρόπο που δεν μπορεί να παρασταθεί γραφικά. Η μεταβολή της εντροπίας του συστήματος, είναι ίδια σε όλες τις περιπτώσεις. |
2-14 ΕΝΤΡΟΠΙΑ
Ο δεύτερος θερμοδυναμικός νόμος, όπως διατυπώθηκε στην προηγούμενη παράγραφο, δεν καταλήγει σε κάποια ποσοτική σχέση. Ποσοτική διατύπωση του 2ου θερμοδυναμικού νόμου έγινε δυνατή με την εισαγωγή μιας νέας έννοιας, της έννοιας εντροπία (σύμβολο S). Η εντροπία εισήχθη από τον Clausius, ο οποίος όρισε τη μεταβολή της εντροπίας (ΔS) συστήματος κατά τη διάρκεια μιας πολύ μικρής αντιστρεπτής μεταβολής, τόσο μικρής ώστε η θερμοκρασία του συστήματος να μπορεί να θεωρηθεί σταθερή, ως το πηλίκο του ποσού θερμότητας ΔQ που απορρόφησε ή απέβαλε το σύστημα προς τη θερμοκρασία του συστήματος.
Μονάδα της εντροπίας στο SI είναι το 1 J/K.
Όταν σε μια αντιστρεπτή μεταβολή το σύστημα απορροφά θερμότητα το ΔQ είναι θετικό, επομένως η εντροπία αυξάνεται. Όταν το σύστημα αποβάλλει θερμότητα το ΔQ είναι αρνητικό και επομένως η εντροπία μειώνεται.
Σε μια αντιστρεπτή μεταβολή κατά την οποία ένα θερμοδυναμικό σύστημα μεταβαίνει από μία αρχική κατάσταση Α σε μια τελική κατάσταση Β, η συνολική μεταβολή της εντροπίας μπορεί να υπολογιστεί αν χωρίσουμε τη διεργασία σε πολύ μικρές μεταβολές (σχ. 2.24), υπολογίσουμε τη μεταβολή της εντροπίας σε κάθε μια από αυτές και αθροίσουμε όλους τους όρους.
Η μεταβολή της εντροπίας ενός συστήματος έχει την ίδια τιμή για όλες τις μεταβολές που οδηγούν από μία αρχική κατάσταση Α σε μία τελική κατάσταση Β, αντιστρεπτές ή μη.
Η μεταβολή της εντροπίας ενός συστήματος εξαρτάται μόνο από την αρχική και τελική του κατάσταση και όχι από το πώς πραγματοποιήθηκε η μεταβολή.
Ίσως βέβαια τα όσα είπαμε μέχρι τώρα να μη βοήθησαν καθόλου στο να κατανοήσετε την ανάγκη εισαγωγής αυτής της νέας έννοιας, της εντροπίας. |
Ελπίζουμε όμως στη συνέχεια να πεισθείτε για την χρησιμότητα του νέου μεγέθους.
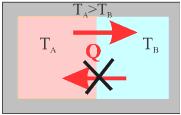
Έστω ένα σύστημα που αποτελείται από δύο σώματα το Α και το Β, με θερμοκρασίες ΤΑ και ΤΒ αντίστοιχα. Το σύστημα είναι μονωμένο από το περιβάλλον (σχ. 2.26). Αν ΤΑ>ΤΒ, θα μετακινηθεί θερμότητα από το σώμα Α στο Β. Το αντίστροφο το αποκλείει ο δεύτερος θερμοδυναμικός νόμος. Ας φανταστούμε μια αντιστρεπτή διαδικασία που μεταφέρει ένα πολύ μικρό ποσό θερμότητας από το σώμα Α στο Β, τόσο μικρό ώστε να μπορούμε να λέμε ότι οι θερμοκρασίες των σωμάτων δεν μεταβλήθηκαν. Η μεταβολή της εντροπίας του σώματος Α θα είναι
Η εντροπία του συστήματος θα μεταβληθεί, κατά
Στο υποθετικό αυτό παράδειγμα, ο δεύτερος νόμος μάς οδήγησε στο συμπέρασμα ότι η εντροπία του απομονωμένου συστήματος αυξήθηκε. Το ίδιο συμβαίνει σε κάθε απομονωμένο σύστημα. Επομένως η έννοια της εντροπίας μάς επιτρέπει να επαναδιατυπώσουμε το δεύτερο νόμο ως εξής:
Κατά τη διάρκεια οποιασδήποτε μεταβολής ενός απομονωμένου συστήματος η εντροπία πάντοτε αυξάνεται.
Η εντροπία του συστήματος αποκτά τη μέγιστη τιμή της όταν επέλθει ισορροπία. Στην περίπτωσή μας το σύστημα ισορροπεί όταν εξισωθούν οι θερμοκρασίες των δύο σωμάτων.
Από ενεργειακή άποψη στο σύστημα αυτό αρχικά θα μπορούσε να λειτουργήσει μια θερμική μηχανή χρησιμοποιώντας σαν δεξαμενή ψηλής θερμοκρασίας το σώμα Α και σαν δεξαμενή χαμηλής θερμοκρασίας το σώμα Β. Η εξίσωση των θερμοκρασιών δεν παρέχει πια αυτή τη δυνατότητα.
Η αύξηση της εντροπίας ενός συστήματος οδηγεί στην ελάττωση της ικανότητας του συστήματος να παράγει ωφέλιμο έργο.
 |
Εικ. 2.13 Τα δύο χάλκινα ελάσματα όταν βρίσκονται σε διαφορετικές θερμοκρασίες αναπτύσσουν μεταξύ τους διαφορά δυναμικού που επιτρέπει τη λειτουργία του ανεμιστήρα. Στην περίπτωση (α) το σύστημα βρίσκεται σε ισορροπία, έχει τη μέγιστη δυνατή εντροπία και δεν έχει δυνατότητα παραγωγής έργου. Στην περίπτωση (β) το σύστημα δεν βρίσκεται σε ισορροπία, η εντροπία του είναι μικρότερη και έχει τη δυνατότητα παραγωγής έργου. |
Σχ. 2.27 (α) Σώμα πολύ χαμηλής θερμοκρασίας εκτελεί μεταφορική κίνηση. Όλα τα μόριά του έχουν την ίδια ταχύτητα (β) Το σώμα έχει συγκρουστεί με ακίνητο εμπόδιο. Οι ταχύτητες των μορίων έχουν τυχαίο προσανατολισμό. Η εντροπία, κατά τη σύγκρουση, αυξήθηκε. |
Μικροσκοπική ερμηνεία της εντροπίας
Στη δεκαετία του 1870 ο Boltzmann συνέδεσε την εντροπία, έννοια μακροσκοπική, με τη μικροσκοπική δομή του συστήματος και έδωσε στην έννοια νέο περιεχόμενο. Ο Boltzmann συνέδεσε το μέγεθος εντροπία με την αταξία που επικρατεί στα δομικά στοιχεία ενός συστήματος.
Όταν μεγαλώνει η αταξία που επικρατεί σε ένα σύστημα μεγαλώνει και η εντροπία του.
Έστω ένα σώμα πολύ χαμηλής θερμοκρασίας (κοντά στο απόλυτο μηδέν), που κινείται με ταχύτητα υ. Τα σωματίδια από τα οποία αποτελείται το σώμα έχουν όλα τη μεταφορική ταχύτητα υ του σώματος και λόγω της πολύ χαμηλής θερμοκρασίας είναι σχεδόν ακίνητα ως προς αυτό. Η κινητική ενέργεια του σώματος είναι, σχεδόν, όση και το άθροισμα των κινητικών ενεργειών των μορίων του. Το σώμα στην πορεία του συναντά ένα εμπόδιο και συγκρούεται. Κατά τη σύγκρουση δε χάνεται ενέργεια. Αν αθροίσουμε τις κινητικές ενέργειες των μορίων του σώματος μετά τη σύγκρουση η ενέργεια που θα πάρουμε είναι όση και πριν. Για να είμαστε πιο ακριβείς, στους υπολογισμούς μας θα πρέπει να συμπεριλάβουμε και την αύξηση των κινητικών ενεργειών των μορίων του εμποδίου γύρω από το σημείο της σύγκρουσης.
Όμως, ενώ πριν συγκρουστεί τα μόρια του σώματος είχαν όλα την ίδια ταχύτητα (σχ. 2.27α) μετά τη σύγκρουση τα μόρια κινούνται άτακτα προς όλες τις κατευθύνσεις (σχ. 2.27β). Πριν τη σύγκρουση το σώμα είχε κάποια κινητική ενέργεια η οποία θα μπορούσε να χρησιμοποιηθεί για την παραγωγή έργου, λόγου χάριν θα μπορούσε να καρφώσει μια πινέζα στον τοίχο. Μετά τη σύγκρουση η συνολική ενέργεια δεν άλλαξε είναι όμως αδύνατον πια να εκμεταλλευτούμε την ενέργεια του συστήματος. Η αταξία του συστήματος αυξήθηκε, μετά τη σύγκρουση. Αν μπορούσαμε να τη μετρήσουμε θα διαπιστώναμε ότι η εντροπία αυξήθηκε.
Από μακροσκοπική άποψη η αύξηση της εντροπίας οδηγεί σε μείωση της ικανότητας για παραγωγή έργου, ενώ από μικροσκοπική άποψη η αύξηση της εντροπίας οδηγεί σε αύξηση της αταξίας του συστήματος. |
|
Εικ. 2.14 Τα Γλαρονήσια, στα βόρεια της Μήλου, έχουν προκύψει από ηφαιστειακή δράση. Η λάβα κατά την ψύξη της πήρε ασυνήθιστα γεωμετρικά, ραβδόμορφα σχήματα. Η εντροπία της λάβας μειώθηκε. Δεν γνωρίζουμε κάτω από ποιες συνθήκες συνέβη αυτό. Εκείνο για το οποίο μπορούμε να είμαστε βέβαιοι είναι το ότι καθώς μειωνόταν η εντροπία της λάβας, αυξανόταν η εντροπία του περιβάλλοντος.
|
2-15 ΥΠΟΛΟΓΙΣΜΌΣ ΤΗΣ ΜΕΤΑΒΟΛΗΣ ΤΗΣ
ΕΝΤΡΟΠΙΑΣ ΣΕ ΜΕΡΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ Αδιαβατική αντιστρεπτή μεταβολή Έστω ότι ένα αέριο, που βρίσκεται αρχικά στην κατάσταση Α (pA, VA, TA), εκτονώνεται αδιαβατικά μέχρι την κατάσταση Β (pB, VB, TB). Η μεταβολή του αερίου παριστάνεται γραφικά στο σχήμα 2.28.
Επειδή πρόκειται για αντιστρεπτή μεταβολή, η μεταβολή της εντροπίας ΔSAB, μπορεί να υπολογιστεί αν χωρίσουμε την διεργασία σε στοιχειώδεις μεταβολές, υπολογίσουμε την μεταβολή της εντροπίας σε κάθε στοιχειώδη μεταβολή και αθροίσουμε όλους του όρους.
Στην αδιαβατική αντιστρεπτή μεταβολή η εντροπία δε μεταβάλλεται.
|
 Σχ. 2.28 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του παραμένει σταθερή Σχ. 2.28 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του παραμένει σταθερή |
 Σχ. 2.29 Το αέριο εκτονώνεται ισόθερμα από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του αερίου αυξάνεται. Σχ. 2.29 Το αέριο εκτονώνεται ισόθερμα από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του αερίου αυξάνεται.
 Σχ. 2.30 Αν χωρίσουμε την κυκλική αντιστρεπτή μεταβολή σε στοιχειώδεις, τότε το άθροισμα των dS, σε όλη την κυκλική διαδρομή, είναι μηδέν. Σχ. 2.30 Αν χωρίσουμε την κυκλική αντιστρεπτή μεταβολή σε στοιχειώδεις, τότε το άθροισμα των dS, σε όλη την κυκλική διαδρομή, είναι μηδέν.
|
Ισόθερμη αντιστρεπτή μεταβολή Έστω ένα αέριο που βρίσκεται αρχικά στην κατάσταση Α και εκτονώνεται ισόθερμα σε θερμοκρασία Τ μέχρι την κατάσταση Β. Το σχήμα 2.29 αποδίδει γραφικά τη μεταβολή του αερίου. Και εδώ επειδή η διεργασία είναι αντιστρεπτή η μεταβολή της εντροπίας υπολογίζεται όπως πριν.
Το άθροισμα στον αριθμητή δίνει το συνολικό ποσό θερμότητας που απορρόφησε το αέριο κατά την μεταβολή. Έτσι, η σχέση γίνεται:
Στην ισόθερμη μεταβολή η θερμότητα που ανταλλάσσει το αέριο με το
Κυκλική μεταβολή
Εφ΄ όσον σε μια κυκλική μεταβολή - αντιστρεπτή ή όχι - το σύστημα επιστρέφει στην αρχική του κατάσταση, η εντροπία του συστήματος δε μεταβάλλεται.
Στην περίπτωση που η κυκλική μεταβολή είναι αντιστρεπτή, αν τη χωρίσουμε σε ν στοιχειώδη τμήματα, ώστε σε καθένα από αυτά να μπορούμε να θεωρήσουμε ότι η θερμοκρασία είναι σταθερή, θα ισχύει:
όπου ΔQ1, ΔQ2, ...,ΔQν τα στοιχειώδη ποσά θερμότητας που προσλαμβάνει ή αποδίδει το σύστημα σε κάθε στοιχειώδες τμήμα της μεταβολής. Σε μία κυκλική αντιστρεπτή μεταβολή λοιπόν ισχύει και
Η μεταβολή της εντροπίας ενός συστήματος εξαρτάται μόνο από την αρχική και τελική του κατάσταση και όχι από το πώς πραγματοποιήθηκε η μεταβολή.

Ίσως βέβαια τα όσα είπαμε μέχρι τώρα να μη βοήθησαν καθόλου στο να κατανοήσετε την ανάγκη εισαγωγής αυτής της νέας έννοιας, της εντροπίας. |
Ελεύθερη εκτόνωση Ένα θερμικά μονωμένο δοχείο χωρίζεται με μεμβράνη σε δύο χώρους. O ένας περιέχει αέριο σε θερμοκρασία Τ και ο άλλος είναι κενός. Κάποια στιγμή η μεμβράνη σπάει και το αέριο εκτονώνεται και καταλαμβάνει αστραπιαία τον όγκο ολόκληρου του δοχείου (σχ.. 2.31). Η διαδικασία εκτόνωσης είναι πολύ βίαιη και με κανένα τρόπο δε μπορεί να χαρακτηριστεί αντιστρεπτή. Θα υπολογίσουμε τη μεταβολή της εντροπίας του αερίου. Μη βιαστείτε να πείτε ότι, αφού το αέριο δεν ανταλλάσσει θερμότητα με το περιβάλλον, σύμφωνα με τη (2.26), θα είναι ΔS=0. Η (2.26) ισχύει μόνο για αντιστρεπτές μεταβολές. Αφού η μεταβολή είναι μη αντιστρεπτή δεν μπορεί να παρασταθεί γραφικά. Γραφικά μπορούν να απεικονισθούν μόνο η αρχική και τελική κατάσταση Α και Β του αερίου, που είναι καταστάσεις ισορροπίας (σχ. 2.32α). Το έργο που παράγει το αέριο για να καταλάβει τον κενό χώρο είναι μηδενικό και, όπως είπαμε, τα τοιχώματα του δοχείου δεν επιτρέπουν τη μεταφορά θερμότητας. Από τον πρώτο θερμοδυναμικό νόμο (Q = ΔU + W) προκύπτει ΔU = 0. Η εσωτερική ενέργεια του αερίου εξαρτάται μόνο από την αρχική και τελική θερμοκρασία και, αφού η εσωτερική ενέργεια δε μεταβάλλεται, η τελική θερμοκρασία του αερίου είναι ίση με την αρχική Τ. Επειδή ΤA = ΤB = Τ η αρχική κατάσταση (Α) και η τελική κατάσταση (Β), βρίσκονται πάνω στην ίδια ισόθερμη καμπύλη (σχ. 2.32β).
Για να υπολογίσουμε τη μεταβολή της εντροπίας θα εκμεταλλευτούμε το ότι αυτή εξαρτάται μόνο από την αρχική και τελική κατάσταση του συστήματος. Μια αντιστρεπτή διαδικασία που έχει τα ίδια άκρα Α και Β είναι η ισόθερμη αντιστρεπτή μεταβολή από την κατάσταση Α στη Β.

Τέλος, επειδή VB > VΑ, η εντροπία του αερίου αυξάνεται (ΔS > 0). Το αποτέλεσμα μπορούσαμε να το προβλέψουμε, αφού στις πραγματικές (μη αντιστρεπτές) μεταβολές η εντροπία ενός απομονωμένου συστήματος αυξάνεται μέχρις ότου το σύστημα έρθει σε κατάσταση θερμοδυναμικής ισορροπίας. |
 Σχ. 2.31 Ελεύθερη εκτόνωση αερίου. Όταν διαρραγεί η μεμβράνη η οποία περιορίζει το αέριο, το αέριο εκτονώνεται ελεύθερα με μη αντιστρεπτό τρόπο και καταλαμβάνει όλο τον όγκο του δοχείου. Σχ. 2.31 Ελεύθερη εκτόνωση αερίου. Όταν διαρραγεί η μεμβράνη η οποία περιορίζει το αέριο, το αέριο εκτονώνεται ελεύθερα με μη αντιστρεπτό τρόπο και καταλαμβάνει όλο τον όγκο του δοχείου.
Σχ. 2.32 Η μεταβολή κατά την ελεύθερη εκτόνωση είναι μη αντιστρεπτή. Γραφικά μπορούν να παρασταθούν μόνο η αρχική και τελική κατάσταση του αερίου Α και Β. Επειδή κατά την ελεύθερη εκτόνωση η αρχική θερμοκρασία του αερίου είναι ίση με την τελική, η αρχική και η τελική κατάσταση του αερίου βρίσκονται πάνω στην ίδια ισόθερμη.
|
ΣΥΝΟΨΗ |
|||||||||||||
Οι ποσότητες που είναι ικανές για την περιγραφή της κατάστασης θερμοδυναμικού συστήματος, αποτελούν τις ανεξάρτητες θερμοδυναμικές μεταβλητές του συστήματος. Μια ποσότητα αερίου βρίσκεται σε κατάσταση θερμοδυναμικής ισορροπίας όταν η πίεση, η πυκνότητα, και η θερμοκρασία του, έχουν την ίδια τιμή σε όλη την έκτασή του. Αντιστρεπτή ονομάζεται η μεταβολή στην οποία υπάρχει η δυνατότητα επαναφοράς του συστήματος και του περιβάλλοντος στην αρχική τους κατάσταση. Οι πραγματικές μεταβολές είναι μη αντιστρεπτές. Το έργο του αερίου για μια πολύ μικρή μεταβολή του όγκου του είναι ΔW = pΔV. Είναι θετικό αν το αέριο εκτονώνεται και αρνητικό αν συμπιέζεται. Το έργο ενός αερίου σε μια αντιστρεπτή μεταβολή είναι ίσο με το εμβαδόν της επιφάνειας από τη γραμμή του διαγράμματος μέχρι τον άξονα V, στο διάγραμμα p-V. Θερμότητα ονομάζεται η μορφή της ενέργειας που μεταφέρεται από ένα σώμα σε ένα άλλο λόγω της διαφοράς θερμοκρασίας των δύο σωμάτων. Κάθε σώμα εμπεριέχει ενέργεια, που είναι το άθροισμα των ενεργειών των σωματιδίων που το απαρτίζουν ως αποτέλεσμα της σχετικής τους κίνησης ως προς το κέντρο μάζας του σώματος και των αλληλεπιδράσεων μεταξύ τους. Αυτή την ενέργεια την ονομάζουμε εσωτερική ενέργεια.
Πρώτος θερμοδυναμικός νόμος: Το ποσό θερμότητας που απορροφά ή αποβάλλει ένα θερμοδυναμικό σύστημα είναι ίσο με το αλγεβρικό άθροισμα της μεταβολής της εσωτερικής του ενέργειας και του έργου που παράγει ή δαπανά το σύστημα. Q = ΔU + W.
Στην ισόχωρη αντιστρεπτή μεταβολή W = 0. Στην ισοβαρή αντιστρεπτή μεταβολή W = p(Vτ - Vα) Αδιαβατική ονομάζουμε εκείνη τη μεταβολή κατά την οποία δε συντελείται μεταφορά θερμότητας από το περιβάλλον προς το σύστημα ή αντίστροφα. Στην αδιαβατική μεταβολή pV γ =σταθ.
Κυκλική ονομάζουμε τη μεταβολή κατά την οποία το σύστημα, μετά από μια διεργασία, επιστρέφει στην αρχική του κατάσταση. Το έργο σε μια κυκλική αντιστρεπτή μεταβολή είναι ίσο με το εμβαδόν που ορίζεται από τη γραμμή του διαγράμματος , στο διάγραμμα p-V. |
Το ποσό θερμότητας που απαιτείται για να μεταβληθεί η θερμοκρασία μιας ποσότητας αερίου κατά ΔΤ είναι Q = n C ΔΤ. Η γραμμομοριακή ειδική θερμότητα με σταθερό όγκο και η γραμμομοριακή ειδική θερμότητα με σταθερή πίεση συνδέονται με τη σχέση Cp = Cv + R. Οι γραμμομοριακές ειδικές θερμότητες Cp και CV για ένα αέριο έχουν σταθερό λόγο.
Η μεταβολή στην εσωτερική ενέργεια ενός αερίου δίνεται από την σχέση ΔU = n Cv ΔΤ. Οι θερμικές μηχανές υποβάλλουν ένα αέριο σε κυκλική μεταβολή κατά τη διάρκεια της οποίας
Δεύτερος θερμοδυναμικός νόμος: Είναι αδύνατο να κατασκευαστεί θερμική μηχανή που να μετατρέπει εξ ολοκλήρου τη θερμότητα σε ωφέλιμο έργο ή να κατασκευαστεί μηχανή που να μεταφέρει θερμότητα από ένα ψυχρό σώμα σε ένα θερμότερο χωρίς να δαπανάται ενέργεια για τη λειτουργία της. Ο Carnot περιέγραψε μια ιδανική κυκλική αντιστρεπτή μεταβολή, που ονομάστηκε κύκλος Carnot, και απέδειξε ότι μια θερμική μηχανή που θα ακολουθούσε αυτόν τον αντιστρεπτό κύκλο θα είχε την μεγαλύτερη δυνατή απόδοση.
Η μεταβολή της εντροπίας κατά τη διάρκεια μιας πολύ μικρής αντιστρεπτής διεργασίας ορίζεται ως το πηλίκο του ποσού
Η μεταβολή της εντροπίας ενός συστήματος εξαρτάται μόνο από την αρχική και τελική κατάστασή του. Περιπτώσεις υπολογισμού μεταβολής της εντροπίας Στην αδιαβατική αντιστρεπτή μεταβολή ΔS = 0
Στην κυκλική μεταβολή ΔSολ = 0
|
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ |
 Σχ. 2.33 Σχ. 2.33
 Σχ. 2.34 Σχ. 2.34
Σχ. 2.35 (α) Τομή του κυλινδρικού δοχείου με τις τρύπες. (β) Τομή του δοχείου μετά την παραμόρφωση. Προσέξτε που βρίσκονται οι τρύπες. (γ) Το δοχείο κρέμεται όρθιο, δεμένο με ένα σκοινί. (δ) Ο ατμός φεύγει από τις τρύπες και το δοχείο στρέφεται.
|
1. Θερμότητα και έργο
Πάρτε ένα λάστιχο (από αυτά που χρησιμοποιούμε για να κλείνουμε μικρά δέματα) και τεντώστε το μπροστά στο πάνω χείλος σας. Θα διαπιστώσετε ότι είναι λίγο θερμότερο από το περιβάλλον. Κρατήστε το έτσι για λίγο και μετά αφήστε το να ξαναπάρει το αρχικό του μήκος. Θα δείτε ότι τώρα φαίνεται λίγο πιο ψυχρό από το περιβάλλον. Πώς εξηγείται αυτό;
2. Η μετατροπή της θερμότητας σε έργο
Σε ένα δοκιμαστικό σωλήνα ρίξτε λίγο νερό και στη συνέχεια κλείστε τον με ένα φελλό. Τοποθετήστε τον όρθιο, με το κλειστό του άκρο προς τα κάτω, στη σιγανή φωτιά ενός καμινέτου. Σε λίγο το νερό θα αρχίσει να βράζει και αν περιμένετε λίγο ο φελλός θα εκτιναχτεί. Περιγράψτε τις ενεργειακές μεταβολές που συμβαίνουν.
3. Κατασκευάστε ένα ατμοστρόβιλο
Θα χρησιμοποιήσετε ένα κλειστό μεταλλικό κουτάκι από αναψυκτικό. Χωρίς να ανοίξετε το κουτάκι ανοίξτε με ένα καρφί δύο τρύπες σε αντιδιαμετρικά σημεία της κυλινδρικής επιφάνειας, που βρίσκονται στο ίδιο ύψος και αδειάστε το περιεχόμενο (σχ. 2.35α). 
Πιέστε με τα χέρια την κυρτή επιφάνεια ώστε το κουτί, να αποκτήσει τέσσερις γωνίες. Πρέπει να πιέσετε το κουτάκι με τέτοιο τρόπο ώστε κάθε τρύπα να βρίσκεται κοντά σε κάποια γωνία (σχ. 2.35β). Βάλτε από τις τρύπες που ανοίξατε περίπου ένα δάχτυλο νερό. Δέστε το κουτάκι από το επάνω μέρος του με σκοινί ώστε να μπορεί να στρέφεται γύρω από τον άξονα του (σχ. 2.35γ). Κρεμάστε το από κάπου και τοποθετήστε ακριβώς από κάτω του ένα γκαζάκι με σιγανή φωτιά. Όταν το νερό αρχίσει να βράζει, ο ατμός θα αρχίσει να φεύγει με ταχύτητα από τις τρύπες και το δοχείο να στρέφεται. |
ΕΡΩΤΗΣΕΙΣ |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 Σχ. 2.36 Σχ. 2.36
 Σχ. 2.37 Σχ. 2.37
 Σχ. 2.38 Σχ. 2.38 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Σχ. 2.39 Σχ. 2.39
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

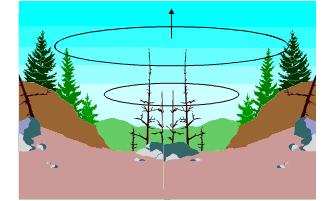
Σχ.2.46 Ποσότητα θερμού αέρα ανεβαίνοντας υφίσταται αδιαβατική εκτόνωση.
 Εικ.2.15 Οι κορυφές του Ολύμπου μένουν χιονισμένες συνήθως σ’ όλη τη διάρκεια του χρόνου. Εικ.2.15 Οι κορυφές του Ολύμπου μένουν χιονισμένες συνήθως σ’ όλη τη διάρκεια του χρόνου. |
ΑΔΙΑΒΑΤΙΚΕΣ ΜΕΤΑΒΟΛΕΣ ΤΟΥ ΑΤΜΟΣΦΑΙΡΙΚΟΥ ΑΕΡΑ Στις αδιαβατικές μεταβολές δε γίνεται ανταλλαγή θερμότητας ανάμεσα στο σύστημα και το περιβάλλον. Πρακτικά, για να θεωρηθεί αδιαβατική η μεταβολή κάποιου αερίου που περιέχεται σε δοχείο θα πρέπει ή το δοχείο να είναι μονωμένο ή η μεταβολή να πραγματοποιείται ταχύτατα ώστε το αέριο να μην προλάβει να ανταλλάξει θερμότητα με το περιβάλλον. Αδιαβατικές μεταβολές συμβαίνουν και στον ατμοσφαιρικό αέρα, δημιουργώντας αυξομειώσεις στη θερμοκρασία του. Πρόκειται για ένα από τα φαινόμενα που λαμβάνουν υπόψη τους οι μετεωρολόγοι όταν μελετούν τις μεταβολές στην ατμόσφαιρα.
Ας θεωρήσουμε την ποσότητα θερμού αέρα έκτασης πολλών τετραγωνικών χιλιομέτρων που βρίσκεται πάνω από μια κοιλάδα (σχ. 2.46). Η ποσότητα αυτή δεν περικλείεται από αδιαβατικά τοιχώματα αλλά, λόγω του μεγάλου όγκου της, παρά το γεγονός ότι τα περιφερειακά στρώματα αναμιγνύονται με αέρα διαφορετικής θερμοκρασίας και πίεσης, το σύνολο της ποσότητας παραμένει ανεπηρέαστο από το περιβάλλον. Η συνολική ποσότητα, δηλαδή, συμπεριφέρεται σα να περικλείεται από σάκο με αδιαβατικά τοιχώματα. Έστω ότι ο αέρας αυτός αρχίζει να ανεβαίνει. Αυτό μπορεί να συμβεί αν βρεθεί σε ψηλότερη θερμοκρασία από τα υπερκείμενα στρώματα οπότε η πυκνότητά του θα είναι μικρότερη από αυτή των υπερκείμενων στρωμάτων. Η πίεση του ατμοσφαιρικού αέρα ελαττώνεται με το ύψος από την επιφάνεια της Γης. Αυτό σημαίνει ότι ο όγκος της ποσότητας στην οποία αναφερόμαστε αυξάνεται και επειδή δεν ανταλλάσσει θερμότητα με το περιβάλλον, η εκτόνωση μπορεί να θεωρηθεί αδιαβατική. Σε μια αδιαβατική εκτόνωση η θερμοκρασία του αερίου μειώνεται. Έχει διαπιστωθεί ότι όταν τέτοιες μάζες αέρα ανεβαίνουν κατά 1 km η θερμοκρασία τους ελαττώνεται κατά 10 οC. Άρα, αν μια θερμή μάζα αέρα του θεσσαλικού κάμπου, θερμοκρασίας 30ο C, ανέβει κατά 3 km, όσο είναι περίπου το ύψος του παρακείμενου Ολύμπου, στην κορυφή του θα έχει θερμοκρασία 0ο C. Έτσι εξηγείται γιατί στα βουνά η θερμοκρασία είναι χαμηλή σε αντίθεση με τη θερμοκρασία στις πεδιάδες. |