Φυσική Τεύχος Β' (Γ Λυκείου Θετικών Σπουδών & Σπουδών Υγείας) - Βιβλίο Μαθητή
ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΑΕΡΙΩΝ 1
Εικόνα
  • Νόμοι αερίων
  • Καταστατική εξίσωση
  • Κινητική θεωρία
  • Κατανομή μοριακών ταχυτήτων
  • Σύνοψη
  • Ασκήσεις
Ένα μόριο αερίου κινείται στο χώρο που καταλαμβάνει το αέριο, συγκρουόμενο με άλλα μόρια κατά τη διαδρομή του. Αν και στην εικόνα φαίνονται στατικά, τα άλλα μόρια κινούνται επίσης μ’ έναν ανάλογο τρόπο. Εικ. 1.1 Ένα μόριο αερίου κινείται στο χώρο που καταλαμβάνει το αέριο, συγκρουόμενο με άλλα μόρια κατά τη διαδρομή του. Αν και στην εικόνα φαίνονται στατικά, τα άλλα μόρια κινούνται επίσης μ’ έναν ανάλογο τρόπο.


Ένα μόριο αερίου κινείται στο χώρο που καταλαμβάνει το αέριο, συγκρουόμενο με άλλα μόρια κατά τη διαδρομή του. Αν και στην εικόνα φαίνονται στατικά, τα άλλα μόρια κινούνται επίσης μ’ έναν ανάλογο τρόπο. Εικ. 1.1 Ένα μόριο αερίου κινείται στο χώρο που καταλαμβάνει το αέριο, συγκρουόμενο με άλλα μόρια κατά τη διαδρομή του. Αν και στην εικόνα φαίνονται στατικά, τα άλλα μόρια κινούνται επίσης μ’ έναν ανάλογο τρόπο.
1-1 ΕΙΣΑΓΩΓΗ

Πολλές από τις σημερινές αντιλήψεις μας για την ύλη και τη θερμότητα έχουν την αφετηρία τους στη μελέτη της συμπεριφοράς των αερίων, για την οποία εργάστηκαν μερικοί από τους πιο σημαντικούς θεωρητικούς και πειραματικούς φυσικούς, στη διάρκεια του αιώνα που πέρασε και στις αρχές του αιώνα μας.

 

Το ενδιαφέρον για τη συμπεριφορά των αερίων δεν είναι μόνο θεωρητικό.  Οι μηχανές των αυτοκινήτων, οι ατμοστρόβιλοι της ΔΕΗ αλλά και μια σειρά από εργαλεία, όπως οι αερόσφυρες (κομπρεσέρ)  που χρησιμοποιούμε για να τρυπάμε  πέτρες, βασίζουν τη λειτουργία τους  σε διαδικασίες στις οποίες συμμετέχουν αέρια.

 

Στα αέρια οι αποστάσεις μεταξύ των μορίων είναι μεγάλες και οι δυνάμεις μεταξύ τους πολύ μικρές. Αυτό εξηγεί γιατί τα αέρια δεν έχουν δικό τους σχήμα και όγκο αλλά «δανείζονται» το σχήμα και τον όγκο του δοχείου που τα περιέχει.

Τα μόρια των αερίων βρίσκονται σε διαρκή κίνηση και συγκρούονται με τα άλλα μόρια ή με τα τοιχώματα του δοχείου. Η κίνηση των μορίων του αερίου, μεταξύ δύο συγκρούσεων, είναι ευθύγραμμη ομαλή, η «μέση ελεύθερη διαδρομή» τους σχετικά μεγάλη και οι ταχύτητες με τις οποίες κινούνται είναι της τάξης των 1600 χιλιομέτρων την ώρα!

 

Σε αντίθεση με ό,τι συμβαίνει στα αέρια, τα μόρια των στερεών βρίσκονται σε μικρή μεταξύ τους απόσταση και οι μεταξύ τους δυνάμεις είναι ισχυρές, γι’ αυτό τα στερεά έχουν ορισμένο σχήμα και όγκο. Τα μόρια των στερεών δε μετατοπίζονται αλλά ταλαντώνονται γύρω από ορισμένη θέση.

 

Στην ενδιάμεση κατάσταση, στα υγρά, οι δυνάμεις ανάμεσα στα μόρια είναι σημαντικές, όχι όμως τόσο μεγάλες όσο στα στερεά, με συνέπεια τα υγρά να έχουν ορισμένο όγκο αλλά όχι δικό τους σχήμα.

 

Στο κεφάλαιο αυτό αρχικά θα μελετήσουμε τους νόμους που διέπουν τη συμπεριφορά των αερίων, όπως αυτή γίνεται αντιληπτή μακροσκοπικά. Στη συνέχεια θα δούμε πώς, με την υπόθεση ότι τα αέρια αποτελούνται από μόρια στα οποία αποδώσαμε ορισμένες ιδιότητες, καταφέραμε να εξηγήσουμε τη συμπεριφορά τους.

 

Μακροσκοπική και μικροσκοπική μελέτη.

 

 

Η περιγραφή - και κατ’ επέκταση η μελέτη ενός φαινομένου - μπορεί να είναι είτε μακροσκοπική είτε μικροσκοπική. Μακροσκοπική λέγεται η μελέτη όταν σ’ αυτή δεν υπεισέρχονται υποθέσεις, θεωρίες ή και μεγέθη που έχουν σχέση με τη δομή ή τη σύσταση των αντικειμένων που συμμετέχουν στο φαινόμενο. Στην αντίθετη περίπτωση η μελέτη λέγεται μικροσκοπική.

Για παράδειγμα, αν συνδέσουμε μια λάμπα στους πόλους μιας μπαταρίας η λάμπα θα ανάψει. Το φαινόμενο μπορεί να μελετηθεί αν μετρηθεί η τάση, η ένταση του ρεύματος, η θερμοκρασία του σύρματος της λάμπας, τα ποσά θερμότητας που εκπέμπει κλπ. Αυτή είναι η μακροσκοπική μελέτη. Αν αντίθετα, προσπαθώντας να εξηγήσουμε το φαινόμενο, αναφερθούμε στο είδος των σωματιδίων που κινούνται μέσα στο σύρμα, στην ταχύτητά τους, στις κρούσεις τους κλπ, μελετάμε μικροσκοπικά το φαινόμενο.

 

Στο χώρο των φυσικών επιστημών η μακροσκοπική και η μικροσκοπική μελέτη των φαινομένων συνήθως συνυπάρχουν. Στα αέρια η μακροσκοπική μελέτη προηγήθηκε της μικροσκοπικής. Στα μέσα του 17ου αιώνα και μετά από μακροσκοπική μελέτη, διατυπώθηκαν οι νόμοι των αερίων από τους Boyle, Charles και Gay-Lussac. Aργότερα (τέλη του 19ου αιώνα) άρχισε η μικροσκοπική τους μελέτη.

Η μικροσκοπική μελέτη βοήθησε να ερμηνεύσουμε τους μακροσκοπικούς νόμους, να εξηγήσουμε τη συμπεριφορά των αερίων (π.χ. με ποιο μηχανισμό το αέριο δημιουργεί πιέσεις) και, γενικά, να κατανοήσουμε σε βάθος την αέρια φάση.

1-2 ΟΙ ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ

H κατάσταση στην οποία βρίσκεται ένα αέριο περιγράφεται μακροσκοπικά από την πίεση, τον όγκο και τη θερμοκρασία του.

 

Τα μεγέθη αυτά (πίεση - όγκος - θερμοκρασία) για ορισμένη ποσότητα αερίου δεν είναι ανεξάρτητα μεταξύ τους αλλά συσχετίζονται. Για παράδειγμα, αν αυξήσουμε τη θερμοκρασία σε μια κλειστή φιάλη που περιέχει αέριο θα αυξηθεί και η πίεση.

 

Οι σχέσεις που συνδέουν τα μεγέθη αυτά προσδιορίστηκαν πειραματικά και αποτελούν τους νόμους των αερίων.

 

Νόμος του Boyle (Μπόιλ, 1627-1691)

 

Η πίεση ορισμένης ποσότητας αερίου του οποίου η θερμοκρασία παραμένει σταθερή είναι αντίστροφα ανάλογη με τον όγκο του.

 

Η μαθηματική διατύπωση είναι:

 

pV=σταθ.    για     Τ=σταθ.

 

α) To αέριο βρί-σκεται μέσα σε ογκομετρικό δοχείο. Το δοχείο με το αέριο περιβάλλεται από λουτρό με νερό του οποίου η θερμο-κρασία διατηρείται σταθερή. Στο δοχείο υπάρχει προσαρ-μοσμένο μανόμετρο για τη μέτρηση της πίεσης του αε-ρίου. β) Στο διάγραμμα πα-ριστάνεται γραφικά η πίεση του αερίου σε συνάρτηση με τον όγκο του, για θερμοκρασίες Τ1 και Τ2 για τις οποίες ισχύει Τ2 > Τ1.

 

Η μεταβολή στην οποία η θερμοκρασία παραμένει σταθερή ονομάζεται ισόθερμη.



















Σχ. 1.1 α) To αέριο βρίσκεται μέσα σε ογκομετρικό δοχείο. Το δοχείο με το αέριο περιβάλλεται από λουτρό με νερό του οποίου η θερμοκρασία διατηρείται σταθερή. Στο δοχείο υπάρχει προσαρμοσμένο μανόμετρο για τη μέτρηση της πίεσης του αερίου. β) Στο διάγραμμα πα-ριστάνεται γραφικά η πίεση του αερίου σε συνάρτηση με τον όγκο του, για θερμοκρασίες Τ1 και Τ2 για τις οποίες ισχύει Τ2 > Τ1.
Σχ. 1.2 α) Το αέριο βρίσκεται μέσα σε δοχείο σταθερού όγκου. Καθώς θερμαίνεται αυξάνεται η πίεσή του.
β) Στο διάγραμμα παριστάνεται γραφικά η μεταβολή της πίεσης σε συνάρτηση με τη θερμοκρασία, για δύο διαφορετικές τιμές του όγκου V1 και V2 με V1<V2.

 

 

 

 

 

 

 

 

Ο νόμος του Charles (Σαρλ, 1746-1823)

 

Η πίεση ορισμένης ποσότητας αερίου του οποίου ο όγκος διατηρείται

σταθερός είναι ανάλογη με την απόλυτη θερμοκρασία του αερίου.

 

Η μαθηματική του διατύπωση είναι:

P  =   σταθ.  για   V=σταθ 
T

 

Ένα μόριο αερίου κινείται στο χώρο που καταλαμβάνει το αέριο, συγκρουόμενο με άλλα μόρια κατά τη διαδρομή του. Αν και στην εικόνα φαίνονται στατικά, τα άλλα μόρια κινούνται επίσης μ’ έναν ανάλογο τρόπο.

Η μεταβολή στην οποία ο όγκος παραμένει σταθερός ονομάζεται ισόχωρη.

 

Στο σχήμα 1.2.β οι διακεκομμένες γραμμές υποδηλώνουν ότι η ευθεία της γραφικής παράστασης προεκτεινόμενη περνάει από την αρχή των αξόνων. Το διακεκομμένο τμήμα της ευθείας αντιστοιχεί σε θερμοκρασίες στις οποίες τα αέρια δεν υπακούουν στο νόμο.

 

Τη θερμοκρασία τη μετράμε σε βαθμούς Κέλβιν (Κ). Η θερμοκρασία αυτή ονομάζεται απόλυτη θερμοκρασία.

 

Το μηδέν της κλίμακας Kelvin αντιστοιχεί στους –273 oC και είναι η  θερμοκρασία κάτω από την οποία είναι αδύνατο να φτάσουμε. Τη θερμοκρασία αυτή τη λέμε και «απόλυτο μηδέν ».

 

Ο νόμος του Gay – Lussac (Γκέι-Λουσάκ, 1778-1850)

 

Ο όγκος ορισμένης ποσότητας αερίου, όταν η πίεσή του διατηρείται

σταθερή, είναι ανάλογος με την απόλυτη θερμοκρασία του.

 

Η μαθηματική διατύπωση του νόμου είναι:

 

V  =   σταθ.   για   p=σταθ 
T

 
α) Καθώς το αέριο θερμαίνεται ο όγκος του αυξάνεται. Η πίεση του αερίου διατηρείται σταθερή με ένα βάρος τοποθετημένο πάνω στο έμβολο. β) Στο διάγραμμα παριστάνεται γραφικά η μεταβολή του όγκου σε συνάρτηση με τη θερμοκρασία, για δυο τιμές της πίεσης

Η μεταβολή στην οποία η πίεση παραμένει σταθερή ονομάζεται ισοβαρής.

 

Ιδανικά αέρια

 

 

Οι τρεις προηγούμενοι νόμοι ισχύουν για τα διάφορα αέρια με μικρές ή μεγάλες αποκλίσεις. Συγκεκριμένα ισχύουν με μεγαλύτερη ακρίβεια για ένα μονοατομικό παρά για ένα πολυατομικό αέριο που βρίσκεται στις ίδιες συνθήκες. Επίσης ισχύουν με μεγαλύτερη ακρίβεια για τα θερμά και αραιά αέρια από ό,τι για τα πυκνά και ψυχρά.

Ας υποθέσουμε τώρα ότι κάποιο αέριο υπακούει με ακρίβεια στους νόμους αυτούς ανεξάρτητα από το αν είναι θερμό ή ψυχρό, πυκνό ή αραιό. Ένα τέτοιο αέριο ακριβώς επειδή στην πραγματικότητα δεν υπάρχει θα ονομάζεται ιδανικό αέριο.

Μακροσκοπικά ιδανικό αέριο, είναι αυτό που υπακούει στους τρεις νόμους των αερίων σε οποιεσδήποτε συνθήκες κι αν βρίσκεται.


Σημείωση:     Οι γραφικές παραστάσεις p-T (σχ. 1.2β) και V-T (σχ. 1.3β) αν αναφέρονταν σε ιδανικό αέριο θα ήταν συνεχείς γραμμές, για όλες τις θερμοκρασίες.

 

1-3 ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΤΩΝ ΙΔΑΝΙΚΩΝ
ΑΕΡΙΩΝ

 

 

Από το συνδυασμό των νόμων των αερίων προκύπτει η εξίσωση:

  pV = nRT (1.1)


H (1.1) ονομάζεται καταστατική εξίσωση των ιδανικών αερίων.
Η R ονομάζεται σταθερά των ιδανικών αερίων και η τιμή της εξαρτάται από τις μονάδες των p, V, T. Στο σύστημα SI, όπου μονάδα πίεσης είναι το Ν/m2 και μονάδα όγκου είναι το m3, η τιμή της R είναι:

R = 8,314 J /mol · K
Σχ. 1.3 α) Καθώς το αέριο θερμαίνεται ο όγκος του αυξάνεται. Η πίεση του αερίου διατηρείται σταθερή με ένα βάρος τοποθετημένο πάνω στο έμβολο.
β) Στο διάγραμμα παριστάνεται γραφικά η μεταβολή του όγκου σε συνάρτηση με τη θερμοκρασία, για δυο τιμές της πίεσης p1 και p2 με p1 > p2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Συνήθως η πίεση μετριέται σε ατμόσφαιρες (atm), ο όγκος σε λίτρα (L) και η τιμή της R είναι:

R = 0,082 L · atm / mol · K

 

O αριθμός των mol του αερίου βρίσκεται από το πηλίκο της ολικής μάζας mολ του αερίου προς τη γραμμομοριακή του μάζα Μ.
  n  =  mολ (1.2)
M

 

Η σχέση (1.1) μπορεί με βάση την (1.2) να πάρει τη μορφή
  pV  =  mολ  R T (1.3)
M

 

Το πηλίκο της συνολικής μάζας του αερίου προς τον όγκο του δίνει την πυκνότητά του:
ρ  =  mολ
V
Έτσι, η σχέση (1.1) μπορεί να πάρει τη μορφή:
p  =  ρ  R T
M

 

Η καταστατική εξίσωση μπορεί να μας δώσει και έναν απλούστερο μακροσκοπικό ορισμό του ιδανικού αερίου:

 

Ιδανικό αέριο είναι το αέριο για το οποίο ισχύει η καταστατική εξίσωση

ακριβώς, σε όλες τις πιέσεις και θερμοκρασίες.

 

Στη συνέχεια, όπου αναφερόμαστε σε αέρια θα θεωρούμε ότι οι συνθήκες είναι τέτοιες ώστε ή καταστατική εξίσωση να ισχύει χωρίς αποκλίσεις.

 
ΠΑΡΑΔΕΙΓΜΑ 1.1

Στην αρχή ενός ταξιδιού η θερμοκρασία των ελαστικών ενός αυτοκινήτου είναι 7 oC. Κατά τη διάρκεια του ταξιδιού τα ελαστικά θερμαίνονται στους 27 oC. Αν στην αρχή του ταξιδιού ο αέρας στο εσωτερικό των ελαστικών βρισκόταν σε πίεση 3atm, πόση θα έχει γίνει η πίεση στο τέλος του ταξιδιού; Υποθέτουμε ότι ο όγκος των ελαστικών παραμένει αμετάβλητος.

Απάντηση:

Aφού ο όγκος των ελαστικών παραμένει σταθερός, η μεταβολή είναι ισόχωρη και ισχύει p/T = σταθ.
Αν p1, T1 είναι η αρχική πίεση και θερμοκρασία και p2, T2 η τελική πίεση και θερμοκρασία των ελαστικών, έχουμε

p1  =  p2  επομένως   p2 = T2 p1= 300K  3atm=3,2atm 
T1 T2 T1 280K

 
ΠΑΡΑΔΕΙΓΜΑ 1.2

Να βρεθεί η πυκνότητα του αέρα μια καλοκαιρινή μέρα που η θερμοκρασία είναι 27oC. Υποθέτουμε ότι η ατμοσφαιρική πίεση είναι 1atm=(1,013x105 N/m2) και ότι ο αέρας συμπεριφέρεται σαν ιδανικό αέριο με γραμμομοριακή μάζα 29x10-3 kg / mol.

Απάντηση:

Η καταστατική εξίσωση γράφεται με τη μορφή:

p  =  ρ  R T  από την οποία προκύπτει  p  =  ρM
M RT

Αντικαθιστώντας στο SI έχουμε

p  =  1,013x105 N / m2·29x10-3kg / mol = 1,18kg / m3
8,314J/(mol K) · 300 K
ΠΑΡΑΔΕΙΓΜΑ 1.3

0,2 mol H2 βρίσκονται σε δοχείο με κινητό έμβολο σε θερμοκρασία Τ1=300 Κ και πίεση 2 atm (κατάσταση Α). Διατηρώντας σταθερή την πίεσή του θερμαίνουμε το αέριο μέχρις ότου η θερμοκρασία του γίνει Τ2=400 Κ (κατάσταση Β). Στη συνέχεια το αέριο εκτονώνεται ισόθερμα μέχρις ότου η πίεσή του γίνει ίση με 1,5 atm (κατάσταση Γ) και μετά ψύχεται με σταθερό όγκο μέχρι η θερμοκρασία του να γίνει Τ1=300Κ (κατάσταση Δ). Τέλος, το αέριο συμπιέζεται ισόθερμα μέχρι να φτάσει στην αρχική του κατάσταση.
Να βρείτε τις τιμές του όγκου της πίεσης, και της θερμοκρασίας που αντιστοιχούν στις καταστάσεις Α, Β, Γ και Δ και να αποδώσετε την παραπάνω διαδικασία σε διαγράμματα με άξονες P-V, P-T, και V-T.
Δίνεται η τιμή της σταθεράς R = 0,082 L · atm/ mol · K

Απάντηση:
  1. A.   Στην κατάσταση Α, το αέριο έχει πίεση pA=2 atm και ΤΑ=300 Κ. Τον όγκο του αερίου μπορούμε να τον υπολογίσουμε από την καταστατική εξίσωση.
    pAVA = nRTA       ή       VA =  0,2 mol · 0,082 L · atm / (mol · K) · 300 K
    2 atm



    από όπου προκύπτει    VA = 2,46 L.

    B.   Στην κατάσταση Β, το αέριο έχει πίεση pB=pA=2 atm και θερμοκρασία ΤB=400 Κ. Ο όγκος του υπολογίζεται από τη σχέση
    VA    =  VB           ή       VΒ =  TΒ VΑ = 400 Κ 2,46 L,
    TA TB TA 300 Κ



    από όπου προκύπτει    VB = 3,28 L.

    Γ.   Στην κατάσταση Γ, το αέριο έχει θερμοκρασία ΤΓ=400 Κ και πίεση pΓ=1,5 atm. Ο όγκος του υπολογίζεται από τη σχέση
    pBVB = pΓVΓ         ή        VΓ =  pΒ VΒ = 2 atm 3,28 L,
    pΓ 1,5 atm



    από όπου προκύπτει VΓ = 4,37 L.

    Δ.   Στην κατάσταση Δ, το αέριο έχει ΤΔ=300 Κ και όγκο VΔ=VΓ=4,37 L. atm και θερμοκρασία. Ο πίεσή του υπολογίζεται από τη σχέση
    pΔ    =  pΓ           ή       pΔ =  TΔ pΓ = 400 Κ 1,5 atm
    TΔ TΓ TΓ 300 Κ



    από όπου προκύπτει    pΔ= 1,125 atm.

    Οι τιμές που βρήκαμε φαίνονται συγκεντρωτικά στον πίνακα

      p(atm) V(L) T(K)
    A 2 2,46 300
    B 2 3,28 400
    Γ 1,5 4,37 400
    Δ 1,125 4,37 300

  2. Με βάση τις τιμές του πίνακα μπορούμε να κατασκευάσουμε τα διαγράμματα:

    εικόνα Σχ. 1.4

 

 

 

 

 

 

 

 

 
1-4 ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ

Η ακριβής μέτρηση της θερμοκρασίας ή της πίεσης ή, ακόμη πιο πέρα, η γνώση των σχέσεων αναλογίας μεταξύ πίεσης, όγκου, αριθμού mol και θερμοκρασίας δεν αρκoύν για να ερμηνεύσουμε τη συμπεριφορά των αερίων.

Η μακροσκοπική συμπεριφορά των αερίων ερμηνεύτηκε ικανοποιητικά, μόλις στο τέλος του 19ου αιώνα, με την κινητική θεωρία των αερίων. Η επιτυχία της κινητικής θεωρίας έδωσε το έναυσμα και για την ανάπτυξη ιδεών για τη δομή της ύλης γενικότερα. Επίσης, όπως συμβαίνει συχνά στην ιστορία της επιστήμης, η ανάγκη επίλυσης πολύπλοκων υπολογιστικών προβλημάτων που έθετε η νέα θεωρία οδήγησε στην ανάπτυξη ενός νέου κλάδου της Φυσικής, της Στατιστικής Φυσικής, που αποτέλεσε αργότερα πολύτιμο εργαλείο για τη θεμελίωση της σύγχρονης Φυσικής, με εφαρμογές που ξεπέρασαν κατά πολύ τον αρχικό λόγο ύπαρξής της.


Σημείο εκκίνησης της κινητικής θεωρίας είναι η υπόθεση ότι τα αέρια αποτελούνται από πολύ μεγάλο πλήθος απειροελάχιστων σφαιριδίων που κινούνται τυχαία (άτακτα) μέσα στο χώρο που καταλαμβάνει το αέριο. Τα σφαιρίδια αυτά δεν είναι τίποτε άλλο από αυτό που σήμερα αποτελεί για τον καθένα κοινό τόπο, τα μόρια του αερίου.

Πιο συγκεκριμένα, για τα ιδανικά αέρια, που προηγουμένως ορίστηκαν μακροσκοπικά ως τα αέρια για τα οποία ισχύει υπό οποιεσδήποτε συνθήκες η καταστατική εξίσωση, η κινητική θεωρία στηρίχτηκε στις εξής παραδοχές:

 

  1. Τα μόρια του αερίου συμπεριφέρονται σαν μικροσκοπικές, απόλυτα ελαστικές, σφαίρες. Έτσι ο συνολικός όγκος των μορίων του αερίου μπορεί να θεωρηθεί αμελητέος σε σχέση με τον όγκο του δοχείου στο οποίο βρίσκεται.
  2. Στα μόρια δεν ασκούνται δυνάμεις παρά μόνο τη στιγμή της κρούσης με άλλα μόρια ή με τα τοιχώματα του δοχείου. Έτσι, η κίνησή τους, στο μεσοδιάστημα μεταξύ δύο κρούσεων, είναι ευθύγραμμη ομαλή.
  3. Οι κρούσεις των μορίων με τα τοιχώματα είναι ελαστικές. Έτσι η κινητική ενέργεια του μορίου δεν μεταβάλλεται μετά την κρούση του με το τοίχωμα
1-5 ΤΑ ΠΡΩΤΑ ΣΗΜΑΝΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ

 

Βασισμένοι στις παραπάνω παραδοχές καταφέραμε να βρούμε σχέσεις που συνδέουν τα μακροσκοπικά μεγέθη, όπως η πίεση και η θερμοκρασία, που μέχρι τώρα μπορούσαμε να τα προσδιορίσουμε μόνο πειραματικά, με τις μέσες τιμές των ταχυτήτων των μορίων του αερίου.

Η πίεση είναι το μονόμετρο μέγεθος που ορίζεται ως το πηλίκο του μέτρου της δύναμης που ασκείται κάθετα σε κάποια επιφάνεια προς το εμβαδόν της επιφάνειας (σχ. 1.5).

 

p  =  ΔF
ΔA

 

Στην περίπτωση ενός αερίου που είναι κλεισμένο σ' ένα δοχείο η πίεση που ασκείται στα τοιχώματα του δοχείου οφείλεται στις δυνάμεις που ασκούν τα μόρια του αερίου στα τοιχώματα κατά τις κρούσεις τους με αυτά (σχ. 1.6).

Η πρώτη σχέση που προκύπτει από την εφαρμογή των νόμων της μηχανικής και των παραδοχών της κινητικής θεωρίας, είναι αυτή που συνδέει την πίεση (p) του αερίου με τις ταχύτητες των μορίων του αερίου.
Βρέθηκε συγκεκριμένα ότι

 

  εικόνα (1.4)

 

 

όπου
Ν
 ο αριθμός των μορίων του αερίου,
 
m
 η μάζα κάθε μορίου,
 
V
 o όγκος του δοχείου και
  εικόνα η μέση τιμή των τετραγώνων των ταχυτήτων των μορίων του
αερίου.

 

Η απόδειξη της σχέσης (1.4) γίνεται στο τέλος της παραγράφου






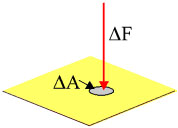Το ΔΑ είναι ένα στοιχειώδες τμήμα της επιφάνειας και ΔF η δύναμη που ασκείται σε αυτό. Σχ. 1.5 Το ΔΑ είναι ένα στοιχειώδες τμήμα της επιφάνειας και ΔF η δύναμη που ασκείται σε αυτό.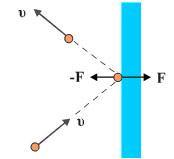

Η κρούση του μορίου με το τοίχωμα θεωρείται ελαστική. Το μέτρο της ταχύτητας του μορίου είναι το ίδιο πριν και μετά την κρούση. Σχ. 1.6 Η κρούση του μορίου με το τοίχωμα θεωρείται ελαστική. Το μέτρο της ταχύτητας του μορίου είναι το ίδιο πριν και μετά την κρούση.

 

 

 

 

 

 

 

 

Μια άλλη, πιο κομψή, μορφή της σχέσης (1.4)  προκύπτει αν λάβουμε υπόψη ότι το γινόμενο Νm είναι η ολική μάζα του αερίου, και ότι το πηλίκο της ολικής μάζας προς τον όγκο V που καταλαμβάνει το αέριο είναι η πυκνότητα ρ του αερίου, οπότε: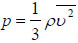

εικόνα

Πολλαπλασιάζοντας και διαιρώντας το δεύτερο μέλος της (1.4) με τον αριθμό 2 προκύπτει η παρακάτω μορφή που συνδέει την πίεση με τη μέση κινητική ενέργεια των μορίων.

 

 
εικόνα
 (1.5)

 

Από την (1.5) προκύπτει

  εικόνα (1.6)

Όμως από την καταστατική εξίσωση γνωρίζουμε ότι

pV  =  nRT  =  N  R T
NA

 

όπου ΝΑ ο αριθμός των μορίων ανά mol (σταθερά Avogadro).

 

Το πηλίκο ΔF εμφανίζεται συχνά στην κινητική θεωρία. Είναι το πηλίκο δύο
ΔA

σταθερών, ονομάζεται σταθερά του Boltzmann (Μπόλτζμαν) και συμβολίζεται με το k.

k  =  R = 1,381x10-23J /(μόριο·Κ)
NA

Μπορούμε λοιπόν να γράψουμε την καταστατική και ως εξής:

 

  pV = NkT (1.7)

 

Εξισώνοντας τα δεύτερα μέλη των σχέσεων (1.6) και (1.7) και λύνοντας ως προς Τ βρίσκουμε

 

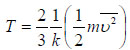εικόνα

Η σχέση αυτή είναι πολύ σημαντική γιατί συνδέει τη θερμοκρασία με τη μέση μεταφορική κινητική ενέργεια των μορίων του αερίου.
Από τη σχέση αυτή, για τη μέση κινητική ενέργεια των μορίων βρίσκουμε

  εικόνα (1.8)

Η τετραγωνική ρίζα της εικόναονομάζεται ενεργός ταχύτητα και συμβολίζεται υεν. Από τη σχέση (1.8) προκύπτει

  εικόνα (1.9)

Απόδειξη της σχέσης  εικόνα

Θεωρούμε ένα κυβικό δοχείο ακμής d. (σχ. 1.7). Το δοχείο θα έχει όγκο V = d3  και εμβαδόν έδρας A = d2. Υποθέτουμε ότι στο δοχείο περιέχεται πολύ μεγάλος αριθμός Ν πανομοιότυπων μορίων αερίου, μάζας m το καθένα, που πληρούν τις προϋποθέσεις της προηγούμενης παραγράφου. Τα τοιχώματα του δοχείου είναι τελείως άκαμπτα, έχουν  πολύ μεγάλη μάζα και δε μετακινούνται.

Κατά τη διάρκεια των κρούσεων των μορίων στα τοιχώματα, τα μόρια ασκούν δυνάμεις σ’ αυτά. Σ’ αυτές τις δυνάμεις οφείλεται η πίεση που ασκεί το αέριο. Οι δυνάμεις αυτές είναι αντίθετες με τις δυνάμεις που ασκούνται από το τοίχωμα στα μόρια  κατά την κρούση (αρχή δράσης- αντίδρασης) και προκαλούν τη  μεταβολή της ορμής των μορίων.

Από το δεύτερο νόμο του Newton γνωρίζουμε ότι F = ΔΡ  , άρα, αν καταφέρουμε να υπολογίσουμε
Δt

τη συνολική μεταβολή της ορμής που υφίστανται τα μόρια στη μονάδα του χρόνου (δηλ. το ρυθμό μεταβολής της ορμής τους) λόγω των κρούσεών τους πάνω σε μία από τις έδρες του δοχείου θα βρούμε και το μέτρο της δύναμης που ασκείται από τα μόρια σ’ αυτή την έδρας.

Μετά, για να βρούμε την πίεση p, αρκεί να διαιρέσουμε τη δύναμη με την επιφάνεια εικόνα .

(Προσοχή :   χρησιμοποιούμε κεφαλαίο P για την ορμή και μικρό p για την πίεση.)

Έστω ένα μόριο που κινείται με ταχύτητα υ1. Αναλύουμε την ταχύτητά του σε τρεις συνιστώσες  ( υ1x , υ1y , υ1z ) (σχ. 1.8). Εξετάζουμε τις κρούσεις  στο τοίχωμα του  δοχείου που είναι κάθετο στη υ1x .

Εφόσον οι κρούσεις είναι απολύτως ελαστικές το μόριο ανακλάται με ταχύτητα ίδιου μέτρου. Η  υ1y και η υ1z  δε μεταβάλλονται ενώ η υ1x αλλάζει φορά.

Η μεταβολή της ορμής που υφίσταται το μόριο κατά την κρούση θα είναι

  ΔΡ1x= -mυ1x -mυ1x = -2mυ1x  

Ο χρόνος που μεσολαβεί ανάμεσα σε δύο διαδοχικές κρούσεις του ίδιου σωματιδίου στην ίδια έδρα θα

είναι Δt = 2d  άρα ο αριθμός κρούσεων στη μονάδα του χρόνου για αυτό το μόριο στην ίδια έδρα θα
υ1x
είναι Δt = υ1x  και ο ρυθμός μεταβολής της ορμής του ( η μεταβολή της ορμής στη μονάδα του
2d
χρόνου ) θα είναι ΔΡ1x    =  -2mυ1x υ1x  = - mυ12x  .
Δt 2d d

 

Η δύναμη που δέχεται το μόριο από το τοίχωμα θα είναι F1x= ΔΡ1x   = - mυ12x  και αντίστοιχα αυτή
Δt d

 

που δέχεται το τοίχωμα από το μόριο θα είναι - F1x= mυ12x  
d

 

Η δύναμη  (ΣFx) που ασκείται πάνω στο τοίχωμα που μελετάμε είναι το άθροισμα όλων των αντίστοιχων όρων που αφορούν κάθε μόριο χωριστά.

Η πίεση (p) που δέχεται η εν λόγω  έδρα από το αέριο θα είναι p = ΣFx  όπου Α = d2
Α

 

Άρα

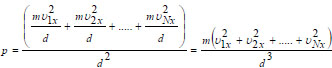εικόνα  

 

 

 

 
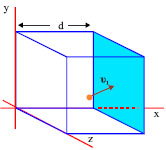Ένα μόριο του αερίου που κινείται με ταχύτητα υ1 μέσα σε κυβικό δοχείο ακμής d.Σχ. 1.7 Ένα μόριο του αερίου που κινείται με ταχύτητα υ1 μέσα σε κυβικό δοχείο ακμής d.

 

 

 

 

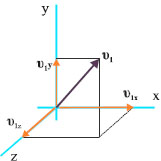Η ταχύτητα αναλύεται σε τρεις συνιστώσες σε τρισορθογώνιο σύστημα συντεταγμένων.Σχ. 1.8 Η ταχύτητα αναλύεται σε τρεις συνιστώσες σε τρισορθογώνιο σύστημα συντεταγμένων.

 

 

 

 

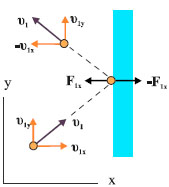Η κίνηση του μορίου στο επίπεδο xy. Σχ. 1.9 Η κίνηση του μορίου στο επίπεδο xy.

 
Οι δυνάμεις που ασκούνται κατά τις κρούσεις των μορίων του αερίου, που περιέχουν τα μπαλόνια, με τα τοιχώματα τεντώνουν το ελαστικό περίβλημα των μπαλονιών. Εικ. 1.3 Οι δυνάμεις που ασκούνται κατά τις κρούσεις των μορίων του αερίου, που περιέχουν τα μπαλόνια, με τα τοιχώματα τεντώνουν το ελαστικό περίβλημα των μπαλονιών.

Πολλαπλασιάζουμε και διαιρούμε το κλάσμα με Ν (το πλήθος των μορίων) οπότε

  εικόνα  

 

Ο όρος  εικόνα είναι η μέση τιμή των τετραγώνων των υx ταχυτήτων και θα τον

συμβολίζουμε εικόνα.

Τελικά εικόνα (1.10)

Τα μόρια κινούνται άτακτα, δεν έχουν δηλαδή καμιά προτίμηση ως προς την κατεύθυνση κίνησής τους, επομένως

  εικόνα  
Γνωρίζουμε ότι γενικά εικόνα  
Εύκολα αποδεικνύεται ότι εικόνα  
επειδή εικόνα  
καταλήγουμε στη σχέση εικόνα

 

Αντικαθιστώντας το ίσον της εικόνα στη σχέση (1.10) και λαμβάνοντας υπόψη ότι d3 =V προκύπτει

εικόνα
ΠΑΡΑΔΕΙΓΜΑ 1-4

 

Να βρεθεί η ενεργός ταχύτητα των μορίων του υδρογόνου σε θερμοκρασία 27oC. Δίνεται ότι η γραμμομοριακή μάζα του υδρογόνου είναι 2x10-3 kg/mol.

 

Απάντηση:

 

Γνωρίζουμε ότι
εικόνα
  

Πολλαπλασιάζοντας αριθμητή και παρονομαστή του υπόρριζου με τον αριθμό Avogadro (ΝΑ) προκύπτει

  εικόνα (1.11)
Όμως k = R  επομένως kNA = R και NAm = M (Μ: η γραμμομοριακή μάζα)
NA
Άρα η σχέση (1.11) γίνεται εικόνα  
Αντικαθιστώντας στο SI εικόνα  = 1,93x103 m/s

Η ταχύτητα αυτή είναι πολύ μεγάλη, είναι περίπου 6900 km/h.

 
1-6 ΚΑΤΑΝΟΜΗ ΜΟΡΙΑΚΩΝ ΤΑΧΥΤΗΤΩΝ

Το πείραμα του Zartman (Ζάρτμαν)

Ο αριθμός των μορίων ενός αερίου, όσο μικρή και αν είναι η ποσότητά του, είναι τεράστιος. Το κάθε μόριο συγκρούεται και αλλάζει ταχύτητα περίπου ένα δισεκατομμύριο φορές το δευτερόλεπτο. Έτσι είναι φανερό ότι η ερώτηση πόσα μόρια έχουν κάποια στιγμή μια συγκεκριμένη ταχύτητα υ δεν έχει νόημα. Μπορούμε όμως να βρούμε τον αριθμό των μορίων dN που έχουν ταχύτητες από υ μέχρι υ+dυ.

 

Το 1920 έγινε το πρώτο πείραμα για τη μέτρηση των μοριακών ταχυτήτων. Το πείραμα που θα περιγράψουμε είναι το πείραμα με το οποίο ο Zartman προσδιόρισε πειραματικά τις ταχύτητες των μορίων ενός αερίου.

 

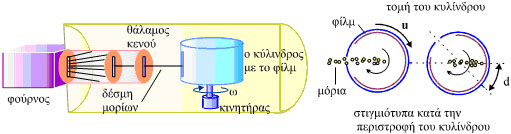
Μέσα σε ένα φούρνο εξαερώνεται μια ουσία. Τα μόρια του ατμού διαφεύγουν από ένα άνοιγμα του φούρνου προς ένα θάλαμο κενού (σχ.1.10). Στο θάλαμο περιστρέφεται με σταθερή γωνιακή ταχύτητα ένας κύλινδρος που φέρει, παράλληλα στον άξονά του, λεπτή σχισμή και στο εσωτερικό της κυρτής του επιφάνειας φέρει ειδικό ευαίσθητο φίλμ. Τα μόρια του ατμού που εισέρχονται από τη σχισμή μέσα στον κύλινδρο συνεχίζουν να κινούνται ευθύγραμμα μέχρι να συναντήσουν το φιλμ, στο οποίο προσκολλώνται και αφήνουν τα ίχνη τους σε απόσταση από το σημείο του φιλμ που βρίσκεται ακριβώς απέναντι από την σχισμή.

Αν η γραμμική ταχύτητα του φιλμ και ο χρόνος που χρειάζεται το μόριο για να διατρέξει τη διάμετρο του κυλίνδρου

η απόσταση ισούται με          d = ut
όμως    t = 2r / u
όπου  η ταχύτητα των μορίων    
και    u = ω r
όπου r η ακτίνα του κυλίνδρου    

 

Επομένως,   d  =   ut   =   ωr  2r  =  2ωr2
υ υ

 

 


Η ταχύτητα των μορίων υπολογίζεται από τη σχέση υ = 2ω r2 / d. Δηλαδή, η μέτρηση της ταχύτητας των μορίων βασίζεται στη μέτρηση της απόστασης d.

 

Στην πράξη, αυτό που μπορούμε να υπολογίσουμε είναι πόσα μόρια πέφτουν σε κάθε σημείο του φιλμ και επομένως να υπολογίσουμε την κατανομή των μορίων στις διάφορες ταχύτητες.

 

Σήμερα είναι δυνατή η μέτρηση των μοριακών ταχυτήτων των αερίων με μεγάλη ακρίβεια.

 

To μοντέλο της πειραματικής διάταξης του Zartman

 



















 

 

 

 

 

 

 

 

 

 

 

Σχ. 1.10 To μοντέλο της πειραματικής διάταξης του Zartman
ΠΑΡΑΔΕΙΓΜΑ 1.5

Από ένα πείραμα ανάλογο με το πείραμα του Zartman, μετρήθηκαν οι ταχύτητες των μορίων και προέκυψε ο παρακάτω πίνακας.

υ (m/s)
 100 200 300 400 500 600 700 800 900 1000 1100
Δυ (m/s)
 0,4 0,25 0,2 0,1 0,2 0,2 0,4 0,5 0,8 1,2 5
ΔΝ (μόρια)
 200 240 400 220 360 240 200 200 160 120 250
ΔΝ/Δυ (μόρια/m/s)
 500 960 2000 2200 1800 1200 500 400 200 100 50

όπου

υ :        ταχύτητες των μορίων
Δυ :   περιοχές ταχυτήτων γύρω από κάθε ταχύτητα  Οι περιοχές ταχυτήτων δεν έχουν όλες το ίδιο
εύρος ώστε να εξασφαλίζεται ότι σε κάθε περιοχή υπάρχει ένας ικανοποιητικός, μετρήσιμος
αριθμός ΔΝ μορίων που κινούνται με ταχύτητες εντός της περιοχής.
ΔΝ :   αριθμός μορίων που έχουν ταχύτητες μέσα στα όρια της κάθε περιοχής ταχυτήτων. Για
παράδειγμα στην πρώτη στήλη 200 μόρια έχουν ταχύτητες από 99,8 m/s έως 100,2 m/s.
ΔΝ/Δυ  :   ο αριθμός των μορίων ανά μοναδιαία περιοχή ταχύτητας
      η μέση τιμή των τετραγώνων των ταχυτήτων των μορίων του αερίου.

Με βάση τα στοιχεία αυτά το διάγραμμα ΔΝ/Δυ=f(υ), της κατανομής των ταχυτήτων των μορίων του αερίου είναι:

 

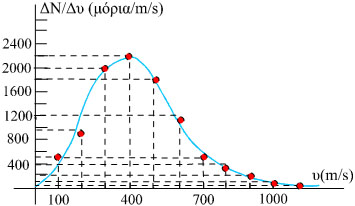
Σχ. 1.11

Σχ. 1.11

 

 

 

 

 

 

 

 

 
Κατανομή κατά Maxwell – Boltzmann (Μάξγουελ - Μπόλτζμαν)

Οι Maxwell και Boltzmann γύρω στο 1860, πολύ πριν γίνει εφικτό να μετρηθούν πειραματικά οι ταχύτητες των μορίων, υπολόγισαν θεωρητικά πώς κατανέμονται τα μόρια ενός αερίου στις διάφορες ταχύτητες.

 

Στο σχήμα 1.12 παριστάνεται γραφικά η συνάρτηση dN/dυ=f(υ) των Maxwell και Boltzmann για  Ν=105 μόρια αζώτου στις θερμοκρασίες 300 Κ και 900 Κ.
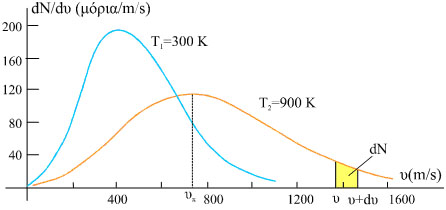Σχ. 1.12 Σχ. 1.12

 

Οι ταχύτητες καλύπτουν ευρεία περιοχή. Η συνάρτηση dN/dυ τείνει στο μηδέν όταν υ → 0 και όταν υ → ∞. Η ταχύτητα που αντιστοιχεί στο μέγιστο της καμπύλης είναι η πιο πιθανή ταχύτητα και συμβολίζεται με υx.

Δύο άλλες ταχύτητες που παρουσιάζουν ενδιαφέρον είναι η μέση ταχύτητα εικόνα και η ενεργός ταχύτητα υεν.

Η μέση ταχύτητα 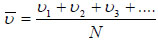εικόνα είναι η μέση τιμή των ταχυτήτων των μορίων του αερίου. Δηλαδή αν οι ταχύτητες των μορίων είναι υ1, υ2, ... και ο αριθμός των μορίων Ν

εικόνα

Η ενεργός ταχύτητα είναι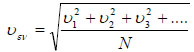

εικόνα

Συχνά, σε διάφορες κατανομές, η μέση τιμή ενός μεγέθους ταυτίζεται με την πιθανότερη τιμή του μεγέθους. Στην κατανομή Maxwell-Boltzmann η εικόνα είναι μεγαλύτερη της υx γιατί προβλέπονται μόρια, έστω και λίγα, με πολύ μεγάλες ταχύτητες (δεν υπάρχει άνω όριο στις ταχύτητες των μορίων). Όσον αφορά τη υεν αποδεικνύεται μαθηματικά ότι η ενεργός τιμή είναι μεγαλύτερη από τη μέση τιμή (βλέπε ένθετο στη σελίδα 32). Έτσι μεταξύ των τριών ταχυτήτων που προαναφέραμε ισχύει υπ < εικόνα < υεν.

 

Αν το τμήμα που έχει κίτρινο χρώμα μπορεί να θεωρηθεί παραλληλόγραμμο -και μπορεί να θεωρηθεί αν το dυ είναι απειροστά μικρό-τότε το εμβαδόν του είναι: dυ x dN/dυ = dN δηλαδή δίνει τον αριθμό dN των μορίων που έχουν ταχύτητες από υ έως υ+dυ. Το εμβαδόν που περικλείεται από την καμπύλη και τον άξονα των υ δίνει το συνολικό αριθμό των μορίων του αερίου.

 

Βλέπουμε ότι όταν η θερμοκρασία του αερίου αυξάνεται η καμπύλη μετατοπίζεται προς τα δεξιά και η κορυφή της χαμηλώνει. Αυτό συμβαίνει γιατί όσο αυξάνεται η θερμοκρασία ο αριθμός των μορίων που έχουν ταχύτητα  μεγαλύτερη από μία δεδομένη τιμή αυξάνεται, η μετατόπιση όμως της καμπύλης δεξιότερα διευρύνει την βάση της και, καθώς το εμβαδόν που περικλείει παραμένει αμετάβλητο (συνολικός αριθμός μορίων), η κορυφή της χαμηλώνει.

 

 
Ludwig Boltzmann (1844-1906) Αυστριακός θεωρητικός φυσικός. Η συνεισφορά του στην κινητική θεωρία και στη στατιστική μηχανική υπήρξε μεγάλη. Εικ. 1.4 Ludwig Boltzmann (1844-1906) Αυστριακός θεωρητικός φυσικός. Η συνεισφορά του στην κινητική θεωρία και στη στατιστική μηχανική υπήρξε μεγάλη.




 

 

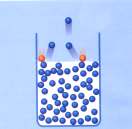Στην εξάτμιση μόρια εγκαταλείπουν την υγρή φάση μόνο από την επιφάνεια του υγρού. Σχ. 1.13 Στην εξάτμιση μόρια εγκαταλείπουν την υγρή φάση μόνο από την επιφάνεια του υγρού.
1-7 ΤΑ ΣΥΜΠΕΡΑΣΜΑΤΑ ΤΗΣ ΚΙΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ
ΕΧΟΥΝ ΕΥΡΥΤΕΡΗ ΕΦΑΡΜΟΓΗ

Η κινητική θεωρία αναπτύχθηκε για να ερμηνεύσει τη συμπεριφορά των αερίων. Όμως κάποια από τα συμπεράσματά της, ποιοτικά τουλάχιστον, ισχύουν για όλες τις μορφές της ύλης. Το συμπέρασμα με την ευρύτερη εφαρμογή είναι η σχέση ανάμεσα στη μέση κινητική ενέργεια των μορίων και τη θερμοκρασία.

Σ’ ένα στερεό τα μόρια ασκούν το ένα στο άλλο ισχυρές δυνάμεις, με αποτέλεσμα να παραμένουν σταθερά «δεμένα» σε κάποιες θέσεις. Η μόνη κίνηση που τους επιτρέπεται είναι μια ταλάντωση γύρω από τη συγκεκριμένη θέση τους. Αν αυξήσουμε τη θερμοκρασία του στερεού, οι ταλαντώσεις των μορίων του γίνονται πιο έντονες (με μεγαλύτερο πλάτος), πάντα όμως γύρω από την ίδια θέση. Βλέπουμε ότι και εδώ η κινητικότητα των μορίων αυξάνει με την αύξηση της θερμοκρασίας. Όταν η θερμοκρασία πάρει ορισμένη τιμή- που τη λέμε θερμοκρασία ή σημείο τήξης του στερεού - τα μόριά του ταλαντώνονται με τόση ενέργεια ώστε να μπορούν να “ξεκολλήσουν” από τη θέση τους. Η οργανωμένη δομή του στερεού καταστρέφεται. Το στερεό τήκεται, περνάει δηλαδή στην υγρή φάση.

 

Η εξαερίωση των υγρών

 

Η δομή των υγρών είναι πολύ πιο κοντά στη δομή των αερίων απ’ ό,τι στη δομή των στερεών. Εδώ τα μόρια δεν έχουν συγκεκριμένες θέσεις, οι δυνάμεις μεταξύ των μορίων όμως είναι τόσο ισχυρές ώστε να μη μπορούμε να τις αγνοήσουμε. Θα έλεγε κανείς ότι τα μόρια έχουν την ελευθερία να ταξιδεύουν, με διάφορες ταχύτητες, στο χώρο που καταλαμβάνει το υγρό. Η ελευθερία των μορίων δεν είναι απόλυτη όπως στα ιδανικά αέρια και η κίνησή τους δεν είναι ευθύγραμμη ομαλή. Παρόλα αυτά, οι ταχύτητες των μορίων στα υγρά ακολουθούν κατανομή που μοιάζει αρκετά με αυτή των Maxwell-Boltzmann για τα αέρια. Αυτό σημαίνει ότι μέσα στο υγρό πάντα υπάρχει ένας αριθμός μορίων που έχουν αρκετά μεγάλες ταχύτητες, που τους επιτρέπουν να “δραπετεύσουν” από τις διαμοριακές έλξεις και να εγκαταλείψουν το υγρό από την ελεύθερη επιφάνειά του. Πρόκειται για το φαινόμενο της εξάτμισης.

Δύο παρατηρήσεις από την καθημερινή ζωή  επαληθεύουν την υπόθεσή μας.

α.          Οποιοδήποτε υγρό εξατμίζεται εντονότερα όταν η θερμοκρασία του είναι

μεγαλύτερη. (Τα ρούχα στεγνώνουν γρηγορότερα το καλοκαίρι).

β.          Όταν εξατμίζεται ένα υγρό η θερμοκρασία του πέφτει. (Όταν κάποιος έχει

πυρετό τού βάζουμε κομπρέσες με νερό στο οποίο προσθέτουμε κάποιο υγρό

που εξατμίζεται γρήγορα στη θερμοκρασία του δωματίου, (π.χ οινόπνευμα),

μ’ αποτέλεσμα το υγρό να διατηρείται δροσερό).

 

Είδαμε ότι όταν αυξάνει η θερμοκρασία η καμπύλη της κατανομής των ταχυτήτων των μορίων των αερίων μετατοπίζεται προς τα δεξιά. Αυτό  σημαίνει ότι, κατά μέσο όρο, οι ταχύτητες των μορίων αυξάνονται. Κάτι ανάλογο συμβαίνει και με τις ταχύτητες των μορίων του υγρού. Είναι λοιπόν αναμενόμενο, όταν θερμαίνεται το υγρό να αυξάνεται ο αριθμός των μορίων της ελεύθερης επιφάνειας του υγρού που έχουν την απαραίτητη κινητική ενέργεια για να εγκαταλείψουν το υγρό.

 

 

Καθώς τα πιο γρήγορα μόριά του εγκαταλείπουν το υγρό, η μέση κινητική ενέργεια των μορίων που απομένουν μικραίνει. Σύμφωνα με τη σχέση εικόνα που συνδέει τη μέση κινητική ενέργεια των μορίων των ιδανικών αερίων με τη θερμοκρασία και, απ’ ό,τι φαίνεται, ισχύει ποιοτικά και για τα υγρά, είναι και θεωρητικά αναμενόμενο να ψύχεται το υγρό.

Εάν τώρα αυξήσουμε τη θερμοκρασία του υγρού, φτάνουμε σε μια θερμοκρασία,  τη θερμοκρασία ή σημείο ζέσεως, στην οποία  ένας πολύ μεγάλος αριθμός μορίων από όλο τον όγκο του και όχι μόνο από την ελεύθερη επιφάνειά του αποκτά την απαραίτητη κινητική ενέργεια για να εγκαταλείψει το υγρό. Έχουμε το φαινόμενο του βρασμού.

Η εξάτμιση και ο βρασμός είναι δύο μορφές του φαινομένου της εξαερίωσης των υγρών.

Από τα προηγούμενα προκύπτει ότι οποιοδήποτε υγρό, με την πάροδο του χρόνου, θα πρέπει να εξατμισθεί πλήρως. Ο χρόνος που θα χρειαστεί γι’ αυτό εξαρτάται από τη θερμοκρασία του περιβάλλοντος, την ποσότητα του υγρού, το εμβαδόν της ελεύθερης επιφάνειάς του καθώς και το είδος του υγρού (πόσο ισχυρές είναι οι δυνάμεις μεταξύ των μορίων του).

Υπάρχει όμως ένα φαινόμενο που κλονίζει λίγο τη βεβαιότητά μας. Γνωρίζουμε όλοι ότι εάν αποθηκεύσουμε ένα υγρό μέσα σ’ ένα μπουκάλι που κλείνει καλά, όσα χρόνια κι αν περάσουν, ακόμη και αν η θερμοκρασία είναι ψηλή και το υγρό από αυτά που εξατμίζονται εύκολα, το υγρό μας δεν πρόκειται να εξατμισθεί πλήρως.

Σ' αυτό το αδιέξοδο φτάσαμε γιατί στους συλλογισμούς μας δεν πήραμε υπόψη κάτι βασικό. Εάν κάποια μόρια του υγρού μπορούν να διαφεύγουν από το υγρό σχηματίζοντας ατμό πάνω από την ελεύθερη επιφάνειά του, γιατί να μην μπορεί να συμβεί και το αντίστροφο, δηλαδή κάποια μόρια να περνούν από την αέρια φάση στην υγρή; Εξάλλου το φαινόμενο της υγροποίησης των ατμών είναι εξίσου οικείο με αυτό της εξάτμισης. Οι υδρατμοί της ατμόσφαιρας υγροποιούνται στα τζάμια όταν αυτά είναι κρύα.

Έχουμε λοιπόν δύο ανταγωνιστικά φαινόμενα, αυτό της εξάτμισης και αυτό της υγροποίησης.

Όταν υπάρχει μια δυναμική ισορροπία ανάμεσα στην εξάτμιση και την υγροποίηση (η ποσότητα υγρού που εξατμίζεται είναι ίση με την ποσότητα του ατμού που υγροποιείται στον ίδιο χρόνο), η ποσότητα του υγρού και η ποσότητα του ατμού πάνω από την ελεύθερη επιφάνειά του παραμένουν σταθερές. Ακριβώς αυτό συμβαίνει στην περίπτωση του υγρού μέσα στο κλειστό μπουκάλι.

Η ταχύτητα με την οποία υγροποιείται ο ατμός εξαρτάται από το πόσο χαμηλή είναι η θερμοκρασία και από την ποσότητα των ατμών πάνω από την ελεύθερη επιφάνεια του υγρού.

Όταν η εξάτμιση και η υγροποίηση βρίσκονται σε ισορροπία η ποσότητα των ατμών που βρίσκονται πάνω από την επιφάνεια  του υγρού είναι η μέγιστη δυνατή για τις δεδομένες συνθήκες και τον διαθέσιμο χώρο. Τότε οι ατμοί λέγονται κορεσμένοι.

Αποκαλύψαμε τώρα, έμμεσα, ένα νέο τρόπο να επιταχύνουμε την εξάτμιση ενός υγρού, εκτός από το να του αυξήσουμε τη θερμοκρασία. Αρκεί να απομακρύνουμε συνεχώς πάνω από την ελεύθερή του επιφάνεια τους ατμούς για να ελαχιστοποιούμε το φαινόμενο της υγροποίησης. Ίσως τώρα καταλαβαίνουμε γιατί ο καλύτερος καιρός για να στεγνώσουν τα απλωμένα ρούχα είναι να κάνει ζέστη αλλά και να φυσάει.
Στο βρασμό μόρια εγκα-ταλείπουν την υγρή φάση από το σύνολο του όγκου του υγρού. Σχ. 1.14 Στο βρασμό μόρια εγκαταλείπουν την υγρή φάση από το σύνολο του όγκου του υγρού.

 

 

 

 

 

 

 

 

 

 

 

 
ΣΥΝΟΨΗ

Ισόθερμη είναι η μεταβολή στην οποία η θερμοκρασία του αερίου διατηρείται σταθερή. Ο νόμος της ισόθερμης μεταβολής είναι

pV=σταθ.   για    Τ= σταθ.

Ισόχωρη ονομάζεται η μεταβολή στην οποία ο όγκος του αερίου διατηρείται σταθερός. Ο νόμος της ισόχωρης μεταβολής είναι

P  =    σταθ.  για   V=σταθ 
T

Ισοβαρής ονομάζεται η μεταβολή στην οποία η πίεση του αερίου διατηρείται σταθερή. Ο νόμος της ισοβαρούς μεταβολής είναι

V  =   σταθ.   για   p=σταθ 
T

Η καταστατική εξίσωση συνδέει την πίεση, τον όγκο και τη θερμοκρασία σε ένα ιδανικό αέριο.

pV = n R T

Μακροσκοπικά, ιδανικό θεωρείται το αέριο στο οποίο η καταστατική εξίσωση ισχύει πάντα.

Μικροσκοπικά, ιδανικό θεωρείται το αέριο του οποίου τα μόρια είναι υλικά σημεία που δεν αλληλεπιδρούν παρά μόνο όταν συγκρούονται. Οι κρούσεις τους με τα άλλα μόρια και με τα τοιχώματα του δοχείου θεωρούνται ελαστικές.

Η πίεση που ασκεί ένα αέριο που βρίσκεται μέσα σε ένα δοχείο οφείλεται στις κρούσεις των μορίων του στα τοιχώματα του δοχείου. Η πίεση του αερίου συνδέεται με τη μέση τιμή των τετραγώνων των ταχυτήτων των μορίων του, με τη σχέση

εικόνα

Η θερμοκρασία του αερίου συνδέεται με τη μέση τιμή των τετραγώνων των ταχυτήτων των μορίων με τη σχέση

εικόνα

Η μέση κινητική ενέργεια των μορίων του ιδανικού αερίου είναι ανάλογη με την απόλυτη θερμοκρασία.

εικόνα

Η ενεργός ταχύτητα των μορίων ιδανικού αερίου είναι

εικόνα

Τα μόρια ενός αερίου δεν έχουν την ίδια ταχύτητα. Οι ταχύτητες των μορίων κάποιας ποσότητας αερίου σε θερμοκρασία Τ ακολουθούν την κατανομή Maxwell - Boltzmann.

Από την κατανομή Maxwell -Boltzmann για τα αέρια μπορούν να βγουν συμπεράσματα που ερμηνεύουν, ποιοτικά, φαινόμενα όπως η εξαερίωση των υγρών ή η υγροποίηση των ατμών.

ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ
1.          Επαληθεύστε το νόμο του Boyle με ένα ….καλαμάκι

 

Βυθίστε ένα καλαμάκι της πορτοκαλάδας μέσα σε ένα ποτήρι με νερό. Κλείστε το επάνω μέρος του με λίγη πλαστελίνη (σχ.1.15α). Βγάλτε το από το ποτήρι. Θα διαπιστώσετε ότι έχετε πάρει μαζί σας και μια ποσότητα νερού.

Πώς το εξηγείτε αυτό; Πόση είναι η πίεση του αέρα που έχει εγκλωβιστεί στο καλαμάκι;

Αναποδογυρίστε το καλαμάκι. Τώρα ο αέρας που έχει εγκλωβιστεί έχει μικρότερο όγκο. Πόση είναι τώρα η πίεση του αέρα;

Μετρήστε στις δύο περιπτώσεις την πίεση και τον όγκο του αέρα και ελέγξτε αν ισχύει η σχέση pV = σταθ.

Την ατμοσφαιρική πίεση θα τη θεωρήσετε 1,013 105 Ν/m2 και το ειδικό βάρος του νερού 104 Ν/m3

Υπόδειξη: Ο όγκος του αέρα στο καλαμάκι είναι V1= l1S και V2= l2S, όπου S η διατομή που έχει το καλαμάκι. H πίεση που δημιουργεί μια στήλη υγρού, στη βάση της είναι ε h (ε: το ειδικό βάρος του υγρού και h το ύψος της στήλης του υγρού). Επειδή το καλαμάκι, στο ανοιχτό του άκρο έχει κάθε στιγμή πίεση ίση με την ατμοσφαιρική (p), η πίεση του αέρα που είναι εγκλωβισμένος μέσα στο καλαμάκι είναι  p1 = p - ε h   όταν το ανοιχτό άκρο βρίσκεται προς τα κάτω (σχ. 1.15β) και
p1 = p + ε h όταν βρίσκεται προς τα πάνω (σχ. 1.15γ).

 

Όταν η εξάτμιση και η υγροποίηση βρίσκονται σε ισορροπία η ποσότητα των ατμών που βρίσκονται πάνω από την επιφάνεια  του υγρού είναι η μέγιστη δυνατή για τις δεδομένες συνθήκες και τον διαθέσιμο χώρο. Τότε οι ατμοί λέγονται κορεσμένοι.

Αποκαλύψαμε τώρα, έμμεσα, ένα νέο τρόπο να επιταχύνουμε την εξάτμιση ενός υγρού, εκτός από το να του αυξήσουμε τη θερμοκρασία. Αρκεί να απομακρύνουμε συνεχώς πάνω από την ελεύθερή του επιφάνεια τους ατμούς για να ελαχιστοποιούμε το φαινόμενο της υγροποίησης. Ίσως τώρα καταλαβαίνουμε γιατί ο καλύτερος καιρός για να στεγνώσουν τα απλωμένα ρούχα είναι να κάνει ζέστη αλλά και να φυσάει.

2.          Επαληθεύστε το νόμο της ισοβαρούς μεταβολής


Πάρτε ένα καλαμάκι της πορτοκαλάδας και κλείστε το ένα άκρο του με πλαστελίνη. Προσπαθήστε να το γεμίσετε με νερό. Θα διαπιστώσετε ότι το νερό που θα ρίξετε δεν γεμίζει το σωλήνα αφού εγκλωβίζεται μια στήλη αέρα. Βάλτε το καλαμάκι σε ένα μπρίκι με νερό, με το κλειστό του άκρο προς τα κάτω. Με ένα μαρκαδόρο σημειώστε το ύψος της στήλης του αέρα για διάφορες τιμές της θερμοκρασίας (θα τη βρείτε με ένα θερμόμετρο) και

δοκιμάστε αν ισχύει η σχέση, V = σταθ. (Αρκεί να ισχύει l  = σταθ. Γιατί;
T T

 

 

Σημείωση: Προσοχή, μη βάλετε το καλαμάκι σας σε πολύ ζεστό νερό. Είναι πολύ πιθανό να παραμορφωθεί. Εξ άλλου σε ψηλές θερμοκρασίες η τάση των ατμών του νερού είναι συγκρίσιμη με την πίεση του αέρα.

 

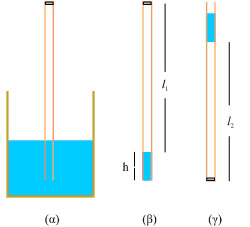Σχ. 1.15Σχ. 1.15

 

 

 

 

 

 

 

 

 

 

 

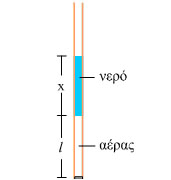Σχ. 1.16.Σχ. 1.16

ΕΡΩΤΗΣΕΙΣ
  Νόμοι των αερίων
  1.1 Ποιο από πα παρακάτω διαγράμματα αντιστοιχεί 1) σε ισοβαρή, και 2) σε ισόθερμη μεταβολή;

 

 

 

εικόνα

 
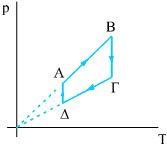Σχ. 1.18 Σχ. 1.18

 

 

 

 

 

 
1.2 Η μεταβολή ΑΒΓΔ που παριστάνεται στο διπλανό διάγραμμα (σχ.1.18) αποτελείται:
α)     Από δύο ισόχωρες και δύο ισόθερμες μεταβολές.
β)     Από δύο ισοβαρείς και δύο ισόθερμες μεταβολές.
γ)     Από δύο ισοβαρείς και δύο ισόχωρες μεταβολές.
Να επιλέξετε τη σωστή απάντηση.

 

 
1.3 Να αντιστοιχίσετε τις μεταβολές της αριστερής στήλης σε σχέσεις της δεξιάς στήλης:
  1) Ισόθερμη μεταβολή    α)  p/v = σταθ.
  2) Ισόθερμη μεταβολή    β)  p/t = σταθ.
  3) Ισόθερμη μεταβολή    γ)  v/t = σταθ.
      δ)  pV = σταθ.
   
1.4 Ποσότητα αερίου θερμαίνεται με σταθερό όγκο. Η πυκνότητά του
α)         Αυξάνεται.
β)         Μειώνεται.
γ)         Μένει σταθερή.
Ποια απάντηση είναι σωστή;
   
1.5

Στο διάγραμμα p-V του σχήματος 1.19 οι καμπύλες (1) και (2) που αναφέρονται σε ισόθερμη μεταβολή δύο αερίων αντιστοιχούν στην ίδια θερμοκρασία. Αυτό μπορεί να οφείλεται στο ότι
α)         Δεν ισχύει στη περίπτωση μας ο νόμος του Boyle.
β)         Τα αέρια έχουν διαφορετικό αριθμό mol.
γ)         Τα αέρια έχουν διαφορετική μοριακή μάζα.

Επιλέξτε τη σωστή απάντηση και δικαιολογήστε την.

 
1.6 Ποιες από τις επόμενες προτάσεις είναι σωστές;
  α) Η καταστατική εξίσωση ισχύει μόνο αν το αέριο αποτελείται από ένα είδος μορίων.
  β) Τα αέρια για τα οποία ισχύει η καταστατική εξίσωση ονομάζονται ιδανικά.
  γ) Σε ορισμένη ποσότητα ιδανικού αερίου η παράσταση pV/T παραμένει σταθερή.
  δ) Η καταστατική εξίσωση ισχύει μόνο στα μονοατομικά αέρια.
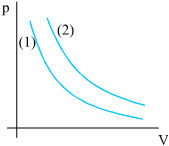Σχ. 1.19Σχ. 1.19

 

 

 
1.7 Ποιο από τα επόμενα διαγράμματα παριστάνει το γινόμενο  ορισμένης ποσότητας αερίου σε συνάρτηση με την απόλυτη θερμοκρασία του;

 

Σχ. 1.20 Σχ. 1.20

 

1.8 Δύο ποσότητες αερίων με αριθμό γραμμομορίων n1 και n2 εκτελούν ισοβαρή μεταβολή στην ίδια πίεση. Ποιο από τα παρακάτω διαγράμματα είναι το σωστό; (n1 > n2).

Σχ. 1.21 Σχ. 1.21

 

 
Κινητική θεωρία
 
1.9 Πώς ορίζεται το ιδανικό αέριο α) μακροσκοπικά και β) μικροσκοπικά;
1.10 Ποιες από τις επόμενες προτάσεις είναι σωστές;
  α) Η θερμοκρασία ενός αερίου είναι ανάλογη με τη μέση κινητική ενέργεια των μορίων του.
  β) Η πίεση ενός αερίου είναι ανάλογη με τη μέση ταχύτητα των μορίων του.
  γ) Οι ενεργές  ταχύτητες των μορίων του οξυγόνου και του αζώτου είναι ίσες, αν τα δύο αέρια βρίσκονται στην ίδια θερμοκρασία.
  δ) Η άτακτη κίνηση των μορίων του αέρα είναι πιο ΄΄γρήγορη ΄΄ το καλοκαίρι από ό,τι το χειμώνα.
   
1.11 Διαθέτουμε δύο δοχεία ίσου όγκου. Το πρώτο περιέχει υδρογόνο και το δεύτερο οξυγόνο, στην ίδια θερμοκρασία. Η μέση κινητική ενέργεια των μορίων του υδρογόνου είναι:
  α) Ίση με τη μέση κινητική ενέργεια των μορίων του οξυγόνου.
  β) Η μισή της μέσης κινητικής ενέργειας των μορίων του οξυγόνου.
  γ) Διπλάσια της μέσης κινητικής ενέργειας των μορίων του οξυγόνου.
  δ) Τετραπλάσια της μέσης κινητικής ενέργειας των μορίων του οξυγόνου.
   
1.12 Η πίεση που ασκεί ένα αέριο δοχείο είναι ανάλογη με
α)         τη μέση τιμή των ταχυτήτων των μορίων.
β)         τον όγκο του δοχείου που το περιέχει.
γ)         την πυκνότητα του αερίου.
δ)         την πίεση που υπάρχει έξω από το δοχείο.
Επιλέξτε τη σωστή απάντηση.
   
1.13 Αέριο συμπιέζεται ισόθερμα στο μισό του αρχικού του όγκου. Η ενεργός ταχύτητα των μορίων του
α)         διπλασιάζεται.
β)         παραμένει σταθερή.
γ)         υποδιπλασιάζεται.
  δ) τα στοιχεία δεν επαρκούν για να κρίνουμε αν η ενεργός ταχύτητα μεταβάλλεται και πώς.
  Επιλέξτε τη σωστή απάντηση.
   
1.14 Ποιες από τις επόμενες προτάσεις που αφορούν στην κατανομή Maxwell – Boltzmann είναι σωστές;
  α) Η κατανομή παριστάνεται γραφικά σε διάγραμμα στο οποίο ο ένας άξονας αναφέρεται στις ταχύτητες (υ) των μορίων του αερίου και ο άλλος στον αριθμό των μορίων που έχουν κάποια ταχύτητα υ.
  β) Η κατανομή Maxwell – Boltzmann δείχνει ότι υπάρχει κάποιο όριο στη μέγιστη ταχύτητα που μπορούν να έχουν τα μόρια του αερίου σε κάποια θερμοκρασία.
  γ) Τα περισσότερα μόρια έχουν ταχύτητες  μεγαλύτερες από την ταχύτητα που αντιστοιχεί στο μέγιστο της καμπύλης.
  δ) Η κατανομή των ταχυτήτων των μορίων ενός αερίου είναι ίδια για όλες τις τιμές της θερμοκρασίας του αερίου.
   
1.15 Πώς ερμηνεύεται η ελάττωση της θερμοκρασίας όταν ένα υγρό εξατμίζεται;

ΑΣΚΗΣΕΙΣ
Νόμοι των αερίων - καταστατική εξίσωση
   
1.16 Δοχείο σταθερού όγκου περιέχει αέρα σε θερμοκρασία 27 οC και πίεση 1atm. Θερμαίνουμε το δοχείο ώστε η θερμοκρασία του αερίου να αυξηθεί κατά 60 οC. Πόση θα γίνει η πίεση;
[Απ: 1,2atm]
1.17 Αέριο βρίσκεται μέσα σε κατακόρυφο κυλινδρικό δοχείο. Το δοχείο κλείνεται με εφαρμοστό έμβολο, πάνω στο οποίο τοποθετούνται διάφορα σταθμά. Το αέριο βρίσκεται σε θερμοκρασία 27 οC και καταλαμβάνει όγκο 0,20 m3. Ψύχουμε το αέριο στους -3 οC. Πόσος θα είναι ο νέος όγκος του αερίου;
[Απ: 0,18 m3]
1.18 Δωμάτιο έχει διαστάσεις. Η θερμοκρασία στο δωμάτιο είναι 27 οC και η πίεση 1atm. Να υπολογιστεί ο αριθμός των mol του αέρα στο δωμάτιο. Δίνονται : 1atm = 1,013x105 N/m2, R = 8,314J / mol K.
[Απ: 1950 mol ]
1.19 Κυλινδρικό δοχείο με διαθερμικά τοιχώματα φράσσεται με εφαρμοστό έμβολο. Το δοχείο περιέχει αέρα πίεσης 1atm και  βρίσκεται μέσα σε λουτρό νερού σταθερής θερμοκρασίας. Πιέζουμε το έμβολο ώστε ο όγκος του αερίου να ελαττωθεί στο 1/3 του αρχικού. Υπολογίστε την τελική τιμή της πίεσης του αερίου.
[Απ: 3atm ]
1.20 2x10-5 mol υδρογόνου βρίσκονται σε δοχείο όγκου V=0,25m3 σε θερμοκρασία 27 οC. Υπολογίστε την πίεση του αερίου. Δίνονται: 
R = 8,314J / mol K , 1atm = 1,013x105 N/m2.
[Απ: 0,2 Ν/m2]
1.21 Αέριο βρίσκεται μέσα σε κυλινδρικό δοχείο. Το πάνω μέρος του δοχείου κλείνεται αεροστεγώς με έμβολο. Ο όγκος του αερίου μέσα στο δοχείο είναι 0,4m3, η θερμοκρασία 300 Κ και η πίεση του 1atm.  Πιέζουμε το έμβολο ώστε ο όγκος του αερίου να γίνει 0,1m3 οπότε παρατηρούμε ότι η θερμοκρασία του έγινε 600 Κ. Υπολογίστε την τελική πίεση του αερίου.
[Απ: 8 atm ]

 

 
1.22 Στο εργαστήριο μπορούν να επιτευχθούν πολύ χαμηλές πιέσεις (υψηλό κενό), έως 13x10-15 atm. Υπολογίστε τον αριθμό των μορίων ενός αερίου σε ένα δοχείο 1L σε αυτή την πίεση και σε θερμοκρασία δωματίου (300Κ). Δίνονται
R = 0,082L· atm / mol · K, NA = 6,023x1023 μόρια/mol.
[Απ: 3,18x108 μόρια]
1.23 Να υπολογιστεί η πυκνότητα του διοξειδίου του άνθρακα σε θερμοκρασία 185 οC και πίεση 1atm (1atm = 1,013x105 N/m2 ). Δίνονται η γραμμομοριακή μάζα του διοξειδίου του άνθρακα 44x10-3 kg / mol και R = 8,314J / mol K.
[Απ: 1,17 kg/m3]
1.24 Ένα αέριο θερμαίνεται με σταθερή πίεση. Να γίνει η γραφική παράσταση της σχέσης ρ=f(θ), όπου ρ η πυκνότητα και θ η θερμοκρασία σε βαθμούς Κελσίου.
1.25 Σε θερμοκρασία θ=27 οC και πίεση p=103N/m2 η πυκνότητα ενός αερίου είναι 8x10-4 kg/m3. Να υπολογιστεί η γραμμομοριακή του μάζα. Δίνεται
R = 8,314J / mol K.
[Απ: 2x10-3 kg/mol ]
1.26 Ένα mol αερίου βρίσκεται σε s.t.p. Διπλασιάζουμε την πίεση διατηρώντας σταθερή τη θερμοκρασία και στη συνέχεια τριπλασιάζουμε τον όγκο διατηρώντας σταθερή την πίεση. Να βρεθούν οι τελικές τιμές πίεσης, όγκου, και θερμοκρασίας.
[Απ: 2 atm, 33,6 L, 819 K ]
Κινητική θεωρία
1.27 Βρείτε τις ενεργές ταχύτητες (υεν) των μορίων του He και των υδρατμών στους 27 οC. Oι αντίστοιχες γραμμομοριακές μάζες είναι 4x10-3 kg / mol και 18x10-3 kg / mol. Δίνεται
R = 8,314J / mol K.
[Απ: 1368 m/s, 644,8 m/s ]
1.28 Εννιά όμοια σωματίδια έχουν ταχύτητες 3, 5, 8, 8, 8, 12, 12, 16, 20. Όλες οι ταχύτητες είναι μετρημένες σε m/s. Υπολογίστε:
α)         τη μέση ταχύτητά τους.
β)         την ενεργό τους ταχύτητα υεν.
[Απ: 10,2 m/s    11,4 m/s ]
1.29 Υπολογίστε την ενεργό ταχύτητα των ατόμων του υδρογόνου στην επιφάνεια του Ήλιου όπου η θερμοκρασία είναι 5800Κ. Δίνεται ότι η γραμμοατομική μάζα του υδρογόνου είναι 1x10-3 kg/mol και R = 8,314J / mol K.
[Απ: 12028m/s ]

ΠΡΟΒΛΗΜΑΤΑ
1.30 Πόσα μπαλόνια όγκου 3 L μπορούμε να φουσκώσουμε με το ήλιο που περιέχεται σε φιάλη όγκου 12 L; Το ήλιο στη φιάλη βρίσκεται υπό πίεση 120 atm, ενώ στα μπαλόνια υπό πίεση 1,2 atm. Υποθέστε ότι τόσο η φιάλη όσο και τα μπαλόνια βρίσκονται στην ίδια θερμοκρασία.
[Απ: 400]
1.31 Ο λεπτός κατακόρυφος σωλήνας του σχήματος 1.22 κλείνεται από μια σταγόνα υδραργύρου Σ και στο τμήμα ΑΣ, ύψους h=27 cm, περιέχει αέρα θερμοκρασίας θ=27 οC. Αν η θερμοκρασία του αέρα γίνει θ΄=127 οC πόσο θα μετακινηθεί η σταγόνα; Η μεταβολή του όγκου του σωλήνα με την αύξηση της θερμοκρασίας θεωρείται αμελητέα.
[Απ: 9cm]
1.32 Κυλινδρικό δοχείο, με τον άξονά του κατακόρυφο, κλείνεται αεροστεγώς στο πάνω μέρος του με έμβολο διατομής Α=0,02m2 και βάρους w=374 Ν. Το αέριο μέσα στο δοχείο καταλαμβάνει όγκο 0,01m3 και βρίσκεται σε θερμοκρασία 27 οC. H ατμοσφαιρική πίεση είναι pατ=1atm.
α)      Πόση είναι η πίεση του αερίου;
β)      Πόσο θα αυξηθεί ο όγκος του αερίου, αν η θερμοκρασία του γίνει
207 οC;
          (1atm = 1,013x105 N/m2)
[Απ: α)   1,2 105 Ν/m2       β)   0,006 m3  ]
1.33 Δοχείο όγκου V, που περιέχει αέρα, έχει στο πάνω μέρος του στρόφιγγα. Αρχικά η στρόφιγγα είναι ανοιχτή και ο αέρας του δοχείου επικοινωνεί με το περιβάλλον. Η ατμοσφαιρική πίεση είναι  pατ=1atm. Θερμαίνουμε το δοχείο, με ανοιχτή τη στρόφιγγα, μέχρι η θερμοκρασία στο εσωτερικό του να γίνει 410 K. Κλείνουμε τη στρόφιγγα, τοποθετούμε το δοχείο σε λουτρό νερού – πάγου. Να υπολογιστεί η τελική πίεση στο εσωτερικό του δοχείου. Η θερμοκρασία στην οποία συνυπάρχει νερό και πάγος είναι Τ=273 Κ.
[Απ: 0,66 atm ]
1.34 Ο κύλινδρος του σχήματος 1.23 χωρίζεται σε δυο μέρη, μέσω εμβόλου που κινείται χωρίς τριβή. Στο τμήμα 1 εισάγονται 2 mg H2 ενώ στο 2 εισάγονται 8 mg Ο2. Ποιος είναι ο λόγος l1 / l2 στην κατάσταση ισορροπίας; Τα αέρια στην κατάσταση ισορροπίας βρίσκονται στην ίδια θερμοκρασία. Οι γραμμομοριακές μάζες για το Η2 και το Ο2 είναι 2x10-3 kg / mol και 32x10-3 kg / mol, αντίστοιχα.
[Απ: 4 ]
1.35 Δύο δοχεία με όγκους V1=0,3 L και V2=0,2 L συνδέονται με λεπτό σωλήνα αμελητέου όγκου. Τα δοχεία περιέχουν αέρα θερμοκρασίας Τ=300 Κ (σχ. 1.24). Αυξάνουμε τη θερμοκρασία στο πρώτο δοχείο κατά 100 βαθμούς και στο δεύτερο κατά 50. Αν η αρχική πίεση ήταν 1atm να υπολογιστεί η τελική της τιμή.
[Απ: 1,26 atm ]

 

 

 

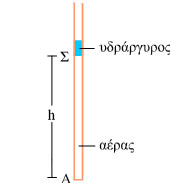Σχ. 1.22 Σχ. 1.22

 

 

 

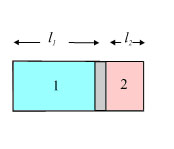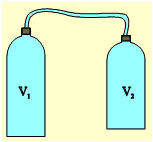εικόνα Σχ. 1.24 Σχ. 1.24

 
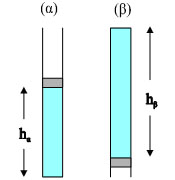Σχ. 1.25 Σχ. 1.25

 

 

 

 
1.36 Το κυλινδρικό δοχείο του σχήματος 1.25 έχει τον άξονά του κατακόρυφο, περιέχει αέρα και κλείνεται με έμβολο. Όταν το δοχείο τοποθετηθεί με τη βάση του προς τα κάτω (σχ.1.25α) το ύψος της στήλης του εγκλωβισμένου αέρα είναι hα=40 cm. Αν το δοχείο αναστραφεί (σχ. 1.25β) το ύψος της στήλης γίνεται hβ=60 cm. Να υπολογιστεί το βάρος του εμβόλου.
Δίνονται pατμ=1,013x105 N/m2 και η διατομή του εμβόλου Α = 10cm2. Η μεταβολή θα θεωρηθεί ισόθερμη.
[Απ: 20,26 N ]
   
1.4 Ποσότητα αερίου θερμαίνεται με σταθερό όγκο. Η πυκνότητά του
α)         Αυξάνεται.
β)         Μειώνεται.
γ)         Μένει σταθερή.
Ποια απάντηση είναι σωστή;
   
  εικόνα

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Η ΕΝΕΡΓΟΣ ΤΑΧΥΤΗΤΑ ΤΩΝ ΜΟΡΙΩΝ ΑΕΡΙΟΥ ΕΙΝΑΙ ΜΕΓΑΛΥΤΕΡΗ ΤΗΣ ΜΕΣΗΣ (ΑΠΟΔΕΙΞΗ)

Έστω ότι οι ταχύτητες των μορίων είναι υi, όπου i=1,2,...N

Υπενθυμίζουμε ότι εικόνα

και εικόνα

Σχηματίζουμε την παράσταση

εικόνα

Η ισότητα ισχύει μόνο στην περίπτωση που όλα τα μόρια έχουν την ίδια κατά μέτρο ταχύτητα, κάτι που για μεγάλους πληθυσμούς μορίων είναι απολύτως αδύνατο. Από τη

μαθηματική επεξεργασία της συνάρτησης dN  = f (υ) που δίνει την κατανομή
dυ

Maxwell-Boltzmann προκύπτει, για ένα αέριο γραμμομοριακής μάζας Μ σε θερμοκρασία Τ, ότι εικόνα

 

ΓΙΑΤΙ ΔΕΝ ΥΠΑΡΧΕΙ ΥΔΡΟΓΟΝΟ ΣΤΗΝ ΑΤΜΟΣΦΑΙΡΑ ΤΗΣ ΓΗΣ

Η κινητική θεωρία των αερίων μάς επιτρέπει να εξηγήσουμε γιατί δεν υπάρχει υδρογόνο στην ατμόσφαιρα της Γης, στην οποία δεσπόζουν το οξυγόνο και το άζωτο.

Η ερμηνεία σχετίζεται με την ταχύτητα διαφυγής από τη Γη, κάτι που θα μας απασχολήσει στην παράγραφο 3-13 αυτού του βιβλίου.

Όταν ένα σώμα βάλλεται από ένα σημείο της επιφάνειας της Γης με αρχική ταχύτητα υο κάνει ευθύγραμμη ή καμπυλόγραμμη κίνηση και επιστρέφει σε αυτή (σχ. 1.26).  Δεν θα επέστρεφε στη Γη μόνο αν η αρχική του ταχύτητα  έπαιρνε την τιμή 11,2 km/s.  Αυτή την ταχύτητα τη λέμε ταχύτητα διαφυγής από την επιφάνεια της Γης. Στο ύψος των 600 km, στα όρια δηλαδή της ατμόσφαιρας της Γης η ταχύτητα διαφυγής έχει τιμή 10,8 km/s (σχ. 1.27).

Η θερμοκρασία της ατμόσφαιρας στο ύψος αυτό είναι περίπου 1500 Κ. Στη
θερμοκρασία αυτή, όπως προκύπτει από τη σχέση εικόνα τα μόρια του
οξυγόνου θα είχαν ενεργό ταχύτητα 1,1 km/s και τα μόρια του υδρογόνου ενεργό ταχύτητα  4,4 km/s.

Ας υποθέσουμε ότι σ’ αυτό το ύψος βρίσκεται μια ποσότητα Ν μορίων οξυγόνου και Ν μορίων υδρογόνου. Από το διάγραμμα της κατανομής των ταχυτήτων κατά Maxwell- Boltzmann, για τα δύο αέρια (σχ. 1.28) προκύπτει ότι, πρακτικά, κανένα μόριο του οξυγόνου δεν έχει ταχύτητα ίση με την ταχύτητα διαφυγής και έτσι όλη η ποσότητα του οξυγόνου παραμένει στη γήινη ατμόσφαιρα. Αντίθετα, υπάρχει μεγάλος αριθμός μορίων υδρογόνου τα οποία έχουν ταχύτητες μεγαλύτερες από την ταχύτητα διαφυγής. Φυσικά δε διαφεύγουν όλα αυτά τα μόρια. Διαφεύγουν μόνο εκείνα που η ταχύτητά τους έχει τον κατάλληλο προσανατολισμό, με την προϋπόθεση ότι δε συγκρούονται με άλλα μόρια.

εικόνα Σχ. 1.28

Στο διάστημα των 4x109 ετών που πέρασαν από τότε που δημιουργήθηκε το πλανητικό μας σύστημα, το υδρογόνο που υπήρχε αρχικά, διαχεόμενο στα ανώτερα στρώματα της ατμόσφαιρας,διέφυγε σιγά - σιγά από το βαρυτικό πεδίο.

Παρατήρηση:  Με τον ίδιο τρόπο εξηγείται γιατί η Σελήνη - στην οποία η ταχύτητα διαφυγής από την επιφάνεια είναι 2,37 km/s - δεν έχει καθόλου ατμόσφαιρα και γιατί στον Άρη (ταχύτητα διαφυγής από την επιφάνεια 4,97km/s) η ατμόσφαιρα είναι πολύ αραιή.

Εικόνα Εάν το σώμα βληθεί με ταχύτητα μικρότερη από την ταχύτητα διαφυγής επιστρέφει στην επιφάνεια της Γης. Σχ. 1.26 Εάν το σώμα βληθεί με ταχύτητα μικρότερη από την ταχύτητα διαφυγής επιστρέφει στην επιφάνεια της Γης. Εάν το σώμα βληθεί με ταχύτητα μεγαλύτερη ή ίση από την ταχύτητα διαφυγής και η κατεύθυνση της αρχικής ταχύτητας είναι κατάλληλη, τότε διαφεύγει οριστικά στο διάστημα. Σχ. 1.27 Εάν το σώμα βληθεί με ταχύτητα μεγαλύτερη ή ίση από την ταχύτητα διαφυγής και η κατεύθυνση της αρχικής ταχύτητας είναι κατάλληλη, τότε διαφεύγει οριστικά στο διάστημα.