Β.1.10. Απόσταση σημείου από ευθεία

Μέρος Β' - Κεφάλαιο 1ο - Βασικές γεωμετικές έννοιες

Β.1.10. Απόσταση σημείου από ευθεία - Απόσταση παραλλήλων

Στη Γεωμετρία, χρησιμοποιούμε την έννοια της απόστασης στις εξής περιπτώσεις:

– Απόσταση σημείου από σημείο, που είναι το μήκος του ευθυγράμμου τμήματος το οποίο τα ενώνει.

– Απόσταση σημείου από ευθεία.

– Απόσταση παραλλήλων ευθειών.

Ας αναζητήσουμε αυτή την έννοια στις παρακάτω δραστηριότητες.

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η

Να βρεις σε ποιο σημείο του δημόσιου αγωγού νερού, στο παρακάτω σχεδιάγραμμα, πρέπει να γίνει η σύνδεση με το σημείο Α του σπιτιού, ώστε ο σωλήνας να έχει το μικρότερο δυνατό μήκος.

Μικροπείραμα

Εικόνα

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η

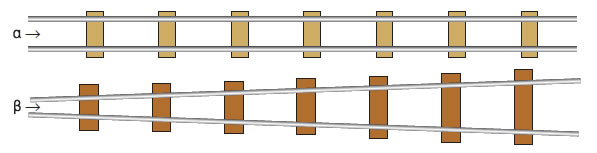
Σε ποια από τις δύο σιδηροτροχιές (α και β) μπορεί να κινηθεί το τραίνο, χωρίς να εκτροχιαστεί; Μπορείς να δικαιολογήσεις την απάντησή σου;

Εικόνα

Μικροπείραμα

Θυμόμαστε - Μαθαίνουμε

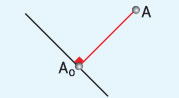
	Απόσταση του σημείου Α από την ευθεία ε ονομάζεται το μήκος του κάθετου ευθυγράμμου τμήματος ΑΑ_Ο από το σημείο Α προς την ευθεία ε.
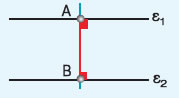
	Απόσταση δύο παραλλήλων ευθειών λέγεται το μήκος οποιουδήποτε ευθυγράμμου τμήματος που είναι κάθετο στις δύο παράλληλες ευθείες και έχει τα άκρα του σ' αυτές, π.χ. το ΑΒ.

Μικροπείραμα Μικροπείραμα

ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ

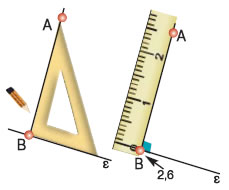
Να βρεθεί η απόσταση του σημείου Α από την ευθεία ε.

Εικόνα

Με τη βοήθεια του γνώμονα σχεδιάζουμε το κάθετο ευθύγραμμο τμήμα ΑΒ από το Α προς την ευθεία ε. Με το υποδεκάμετρο μετράμε το ευθύγραμμο τμήμα ΑΒ και το βρίσκουμε π.χ. 2,6 cm. Άρα, η απόσταση του σημείου Α από την ευθεία ε είναι, στην περίπτωση αυτή, 2,6 cm.

Μικροπείραμα

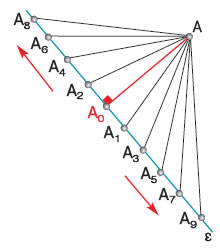
Να βρεθεί σημείο της ευθείας ε, η απόσταση του οποίου από ένα σημείο Α εκτός αυτής να είναι η ελάχιστη.

Από το σημείο Α φέρνουμε το κάθετο τμήμα ΑΑ_ο στην ευθεία ε και συνδέουμε το σημείο Α με διάφορα σημεία Α₁, Α₂, Α₃, Α₄, Α₅, Α₆, Α₇, Α₈ και Α₉ της ε. Μετράμε τις αποστάσεις του Α από αυτά και παρατηρούμε ότι αυτές μεγαλώνουν συνεχώς όσο απομακρυνόμαστε αριστερά και δεξιά από το Α_ο, άρα η ελάχιστη απόσταση είναι το ευθύγραμμο τμήμα ΑΑ_ο. Επομένως το Α_ο, είναι το ζητούμενο σημείο και ονομάζεται ίχνος της κάθετης από το Α.

Μικροπείραμα

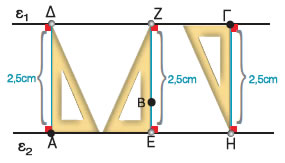
Να σχεδιαστούν και να συγκριθούν τα ευθύγραμμα τμήματα που διέρχονται από τα σημεία Α, Β και Γ και εκφράζουν τις αποστάσεις των παραλλήλων ευθειών ε₁ και ε₂.

Φέρνουμε τις κάθετες ΑΔ, ΕΒΖ και ΗΓ από τα σημεία Α, Β και Γ στις ευθείες ε₁ και ε₂. Μετράμε τα ευθύγραμμα τμήματα ΑΔ, ΕΖ και ΗΓ και βρίσκουμε ότι είναι όλα μεταξύ τους ίσα. Άρα η απόσταση των παραλλήλων ευθειών ε₁ και ε₂ είναι σταθερή και ίση με 2,5 cm.

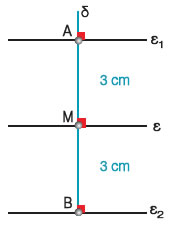
Να σχεδιαστούν δύο ευθείες ε₁ και ε₂ παράλληλες προς μια ευθεία ε, που να απέχουν από αυτή 3 cm.

Σε τυχαίο σημείο Μ της ε σχεδιάζουμε ευθεία δ κάθετη στην ε. Πάνω στην ευθεία δ βρίσκουμε με το υποδεκάμετρο δύο σημεία Α και Β έτσι, ώστε να είναι: ΜΑ = ΜΒ = 3 cm. Από τα Α και Β, με τον γνώμονα, σχεδιάζουμε ευθείες ε₁ και ε₂ κάθετες στην ε. Οι ευθείες αυτές είναι οι ζητούμενες, γιατί η απόσταση τους από την ε είναι 3 cm.

ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ

Εικόνα

Συμπλήρωσε τα παρακάτω κενά:

(α)	Το μήκος του καθέτου ευθυγράμμου τμήματος ΑΑ_ο από το σημείο Α προς την ευθεία ε ονομάζεται ................................ του σημείου Α από την ευθεία.
(β)	Το μήκος οποιουδήποτε ευθυγράμμου τμήματος, που είναι κάθετο σε δύο παράλληλες ευθείες και έχει τα άκρα του σ' αυτές λέγεται ................................. των δύο παραλλήλων ευθειών.

Σημείωσε, πάνω σε μια ευθεία ε, με τη σειρά, τα σημεία Γ, Β και Δ, έτσι ώστε να είναι ΓΒ = ΒΔ = 3 cm. Χάραξε μια ευθεία, που να διέρχεται από το Β κάθετη στην ε. Πάνω στην κάθετη αυτή να σημειώσεις ένα σημείο Α, που να απέχει από το Β απόσταση ΑΒ = 4 cm. Να συγκρίνεις μετρώντας με το υποδεκάμετρο τα ευθύγραμμα τμήματα ΑΓ και ΑΔ.

Να επαναλάβεις την προηγούμενη άσκηση, εάν είναι: ΓΒ = 6 cm, ΒΔ = 15 cm, ΑΒ = 8 cm.

Να σχεδιάσεις δύο μη αντικείμενες ημιευθείες Οx και Οy. Να πάρεις στην Οx, τα σημεία Α, Β και Γ, τέτοια ώστε να είναι: ΟΑ = ΑΒ = ΒΓ = 2 cm. Να ορίσεις στην Οy ένα σημείο Α΄, ώστε να είναι ΟΑ΄ = 1,6 cm και να σχεδιάσεις την ευθεία ΑΑ΄. Στη συνέχεια να φέρεις από τα Β και Γ παράλληλες προς την ΑΑ΄ και να ονομάσεις Β΄ και Γ΄ τα σημεία στα οποία αυτές τέμνουν αντίστοιχα την Οy. Να μετρήσεις με το υποδεκάμετρο τα μήκη των τμημάτων Α΄ Β΄ και Β΄Γ΄. Τι παρατηρείς;

Nα σχεδιάσεις μια ευθεία ε και τέσσερα σημεία Α, Β, Γ και Δ, τα οποία να βρίσκονται στο ένα από τα ημιεπίπεδα που χωρίζει η ε το επίπεδο, και το καθένα ν' απέχει απ' αυτή 3,2 cm. Να φέρεις από καθένα απ' αυτά τα σημεία ευθεία παράλληλη προς την ε. Πόσες παράλληλες ευθείες υπάρχουν στο σχήμα σου;

Nα σχεδιάσεις δύο παράλληλες ευθείες ε₁ και ε₂ των οποίων η απόσταση να είναι 35 mm. Να βρεις πέντε σημεία Α, Β, Γ, Δ και Ε, που να ισαπέχουν από τις ε₁ και ε₂. Να σχεδιάσεις μια ευθεία ε από το Α παράλληλη προς τις ε₁ και ε₂. Τα σημεία Β, Γ, Δ και Ε ανήκουν ή όχι στην ε;

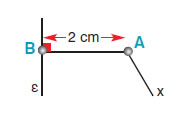
Να αντιγράψεις σε τετραγωνισμένο χαρτί το παρακάτω σχήμα και να βρεις ένα σημείο Γ της ημιευθείας Αx, που ν' απέχει 3 cm από την ευθεία ε.

ΔΡΑΣΤΗΡΙΟΤΗΤΑ ΠΑ ΤΟ ΣΠΙΤΙ

Ένα πλοίο ακολουθεί ευθεία πορεία ΑΒ, που είναι συνολικά 21Κm. Όταν βρίσκεται στη θέση Α απέχει 10 Κm από ένα φάρο Φ και όταν βρίσκεται στη θέση Β απέχει 17 Κm από τον ίδιο φάρο. Να σχεδιάσεις το σχήμα ΦΑΒ παίρνοντας 1 cm για απόσταση ίση με 1 Κm και να υπολογίσεις πόσο κοντά από το φάρο πέρασε το πλοίο