- 4.45 Στην περιφέρεια ενός τροχού, μάζας Μ= 2 kg και ακτίνας R=0,5 m, που στρέφεται με γωνιακή ταχύτητα ω= 100 rad/s γύρω από τον άξονά του ασκείται σταθερή δύναμη F, εφαπτομενική στον τροχό. Ο τροχός σταματάει μετά από 5s. Να υπολογίσετε:
α) τη γωνιακή επιτάχυνση (επιβράδυνση) του τροχού,
β) το μέτρο της δύναμης F.
Η ροπή αδράνειας του τροχού είναι I =  ML2. ML2.
[Απ : 20 rad/s2, 10N]
4.46 Οριζόντια ομογενής ράβδος, μήκους L=1 m, μπορεί να στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το ένα άκρο της (σχ.4.60). Ποια είναι η γωνιακή επιτάχυνση της ράβδου, τη στιγμή που, από την οριζόντια θέση, αφήνεται ελεύθερη;
- Η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής της είναι I =
 ML2 και η επιτάχυνση της βαρύτητας g = 10m/s2 ML2 και η επιτάχυνση της βαρύτητας g = 10m/s2
[Απ: 15 rad/s2 ]
Στροφορμή - αρχή διατήρησης της στροφορμής
4.47 Δύο σφαίρες, που η καθεμιά έχει μάζα m= 100 g συνδέονται μεταξύ τους με αβαρή ράβδο, όπως στο σχήμα 4.61. Το σύστημα περιστρέφεται σε οριζόντιο επίπεδο με γωνιακή ταχύτητα ω= 16 rad/s, γύρω από τον κατακόρυφο άξονα z'z. Να υπολογίσετε τη στροφορμή του συστήματος.
Δίνεται l = 0,8m
[Απ: 5,12 kg m2/s ]
4.48 Υπολογίστε τη στροφορμή ενός τροχού μάζας Μ = 2 kg και ακτίνας R=0,4 m, που στρέφεται με γωνιακή ταχύτητα ω=10 rad/s γύρω από τον άξονά του. Θεωρήστε ότι η μάζα του τροχού βρίσκεται συγκεντρωμένη στην περιφέρειά του.
[Απ: 3,2 kg m2/s ]
4.49 Οριζόντιος δίσκος ακτίνας 20 cm και μάζας 1 kg στρέφεται με συχνότητα 2 Hz γύρω από κατακόρυφο άξονα που περνάει από το κέντρο του. Από κάποιο ύψος αφήνεται ένα κομμάτι λάσπη μάζας 100gr, που κολλάει στο δίσκο σε απόσταση 10 cm από τον άξονα περιστροφής. Να υπολογίσετε τη νέα συχνότητα περιστροφής.
- Η ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του είναι I =
 ML2. ML2.
[Απ: 1,9 Hz ]
|

Σχ. 4.60
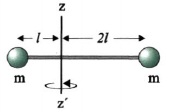
Σχ.4.61 |
|