 Σχ. 5.25 Ένα ηλεκτρόνιο αφήνεται μέσα σε ομογενές ηλεκτρικό πεδίο. Σχ. 5.25 Ένα ηλεκτρόνιο αφήνεται μέσα σε ομογενές ηλεκτρικό πεδίο.
|
5-8 ΚΙΝΗΣΕΙΣ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙΔΙΩΝ ΣΕ
ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ Δύο παράλληλες μεταλλικές πλάκες φορτισμένες με αντίθετα φορτία, όπως στο σχήμα, δημιουργούν ανάμεσά τους ομογενές ηλεκτρικό πεδίο. Αν μέσα σ’ αυτό το πεδίο βρεθεί ένα φορτισμένο σωματίδιο θα δεχτεί σταθερή δύναμη F=Eq και θα αποκτήσει σταθερή επιτάχυνση α = Eq/m.
Α. Κίνηση χωρίς αρχική ταχύτητα
Ένα ηλεκτρόνιο (Σχ. 5.25) αφήνεται πολύ κοντά στην αρνητική πλάκα. Το ηλεκτρόνιο θα δεχτεί από το πεδίο δύναμη σταθερού μέτρου F = Ee (E: η ένταση του πεδίου και e: το στοιχειώδες ηλεκτρικό φορτίο) αντίρροπη της Ε και θα κινηθεί ευθύγραμμα ομαλά επιταχυνόμενα, με επιτάχυνση α = F / me Η κίνηση του ηλεκτρονίου περιγράφεται από τις σχέσεις
από τις οποίες μπορούμε να υπολογίσουμε:
1. Πόσο χρόνο χρειάζεται το ηλεκτρόνιο για να φτάσει στην απέναντι πλάκα;
|
2. Με ποια ταχύτητα φτάνει το ηλεκτρόνιο στη θετική πλάκα;
Αντικαθιστώντας στη σχέση υ = at το χρόνο που βρήκαμε παραπάνω βρίσκουμε
Ας κάνουμε μια αριθμητική εφαρμογή για να δούμε για ποιας τάξης μεγέθους ταχύτητες και χρόνους μιλάμε. Αν η διαφορά δυναμικού ανάμεσα στις μεταλλικές πλάκες είναι V = 1kV και η απόσταση μεταξύ τους d = 5 mm η ένταση του πεδίου στο εσωτερικό του θα είναι Ε=2 x 105 N/C, η δύναμη που θα δεχθεί το ηλεκτρόνιο θα έχει μέτρο F=3,2 x 10-14 N (e=1,6 x 10-19 C), η επιτάχυνση θα είναι α=3,5 x 1016 m/s2 (me=9,1 x 10-31 kg), ο χρόνος για να φτάσει στον απέναντι οπλισμό t1 = 5,3 x 10-10s και η τελική του ταχύτητα υ1 =1,9 x 107 m/s
Διατάξεις που χρησιμοποιούν τον παραπάνω μηχανισμό (επιτάχυνση φορτισμένου σωματιδίου σε ομογενές ηλεκτροστατικό πεδίο) έχουν ευρεία εφαρμογή σε μια σειρά από συσκευές όπως ο φασματογράφος μάζας, ο καθοδικός σωλήνας και άλλες.
Β. Κίνηση με αρχική ταχύτητα κάθετη στις δυναμικές γραμμές
Θεωρούμε ότι οι παράλληλες μεταλλικές πλάκες του σχήματος 3.26 είναι φορτισμένες με φορτία +q και -q, έχουν μήκος L, απέχουν μεταξύ τους απόσταση d και η διαφορά δυναμικού τους είναι V. Ένα ηλεκτρόνιο εισέρχεται με αρχική ταχύτητα υ0 κάθετη στις δυναμικές γραμμές του ομογενούς πεδίου που σχηματίζεται ανάμεσα στις πλάκες. Το ηλεκτρόνιο κατά την κίνησή του μέσα στο ομογενές πεδίο δέχεται σταθερή δύναμη F.
Για τη μελέτη μιας τέτοιας κίνησης θα εφαρμόσουμε την αρχή της ανεξαρτησίας των κινήσεων.
Διαλέγουμε δύο άξονες πάνω στους οποίους αναλύουμε την κίνηση. Εδώ θα επιλέξουμε έναν άξονα παράλληλο στις δυναμικές γραμμές κι έναν κάθετο σ’ αυτές.
Αφού η διαφορά δυναμικού ανάμεσα στις φορτισμένες πλάκες είναι V, η ένταση του ηλεκτρικού πεδίου σε οποιοδήποτε σημείο του χώρου μεταξύ των πλακών
Στον άξονα x το ηλεκτρόνιο δεν δέχεται δύναμη και έτσι θα κινηθεί ευθύγραμμα ομαλά, διατηρώντας την αρχική του ταχύτητα υo .
Στον άξονα y δέχεται καθ’ όλη τη διάρκεια της κίνησης μια δύναμη σταθερή,
ηλεκτρόνιο θα εκτελέσει σ’ αυτό τον άξονα ομαλά επιταχυνόμενη κίνηση χωρίς αρχική ταχύτητα με επιτάχυνση
|
 Εικ. 5.36 To ηλεκτρόνιο εισέρχεται στο ηλεκτρικό πεδίο με ταχύτητα κάθετη στις δυναμικές γραμμές. Η δύναμη που δέχεται από το πεδίο το αναγκάζει να διαγράψει παραβολική τροχιά. Εικ. 5.36 To ηλεκτρόνιο εισέρχεται στο ηλεκτρικό πεδίο με ταχύτητα κάθετη στις δυναμικές γραμμές. Η δύναμη που δέχεται από το πεδίο το αναγκάζει να διαγράψει παραβολική τροχιά.
 Εικ. 5.2 Πειραματική διάταξη για τη μελέτη της απόκλισης μιας δέσμης ηλεκτρονίων μέσα σε ομογενές ηλεκτρικό πεδίο Εικ. 5.2 Πειραματική διάταξη για τη μελέτη της απόκλισης μιας δέσμης ηλεκτρονίων μέσα σε ομογενές ηλεκτρικό πεδίο
|
 Σχ. 5.27 Όταν το ηλεκτρόνιο εξέρχεται από το πεδίο έχει αποκλίνει κατά y1 από την αρχική του διεύθυνση και η ταχύτητα του είναι συνισταμένη της αρχικής ταχύτητας υο και της ταχύτητας υ1y. Σχ. 5.27 Όταν το ηλεκτρόνιο εξέρχεται από το πεδίο έχει αποκλίνει κατά y1 από την αρχική του διεύθυνση και η ταχύτητα του είναι συνισταμένη της αρχικής ταχύτητας υο και της ταχύτητας υ1y. |
Τελικά, στον άξονα x θα ισχύουν:
Από τις σχέσεις αυτές μπορούν να υπολογισθούν:
1. Χρόνος παραμονής στο πεδίο
Το ηλεκτρόνιο θα εξέλθει από το πεδίο όταν, στον άξονα x θα έχει μετατοπιστεί κατά L. Αν στην σχέση (5.32) θέσουμε όπου x το L και λύσουμε ως προς t προκύπτει:
2. Απόκλιση από την αρχική διεύθυνση κίνησης στην έξοδο
Εάν στη σχέση (5.34) θέσουμε στη θέση του t το χρόνο παραμονής στο πεδίο βρίσκουμε την κατακόρυφη απόκλιση y του ηλεκτρονίου από την αρχική του θέση, κατά την έξοδό του από το πεδίο.
3. Ταχύτητα εξόδου από το πεδίο
Κατά την έξοδό του από το πεδίο, η ταχύτητα του ηλεκτρονίου στον άξονα x θα είναι υ1x = υo ενώ στον y θα είναι υ1y = ayt1 και από τις (5.30) και (5.35)
H ταχύτητα που θα έχει το ηλεκτρόνιο κατά την έξοδό του θα είναι
4. Η εξίσωση της τροχιάς του ηλεκτρονίου
Η εξίσωση της τροχιάς του ηλεκτρονίου είναι η σχέση που συνδέει τις μετατοπίσεις του στους άξονες x και y. Λύνουμε την (5.32) ως προς t και αντικαθιστούμε στην (5.34) λαμβάνοντας υπόψη και την (5.30). Βρίσκουμε έτσι μια σχέση y = f (x) |
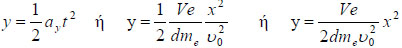
Πρόκειται για μια σχέση της μορφής y = αx2, άρα η τροχιά του ηλεκτρονίου είναι παραβολική.
Στη μελέτη της κίνησης του ηλεκτρονίου μέσα στο ομογενές ηλεκτρικό πεδίο δε λάβαμε καθόλου υπόψη το βάρος του. Αυτό έγινε γιατί το βάρος είναι αμελητέο συγκριτικά με την F. Ενδεικτικά αναφέρουμε ότι το βάρος ενός ηλεκτρονίου είναι we = 8,9 x 10-30 N ενώ η ηλεκτρική δύναμη που δέχεται ένα ηλεκτρόνιο στο εσωτερικό ενός ομογενούς ηλεκτρικού πεδίου σαν αυτό που περιγράψαμε με διαφορά δυναμικού V=1 kV και απόσταση μεταξύ των πλακών d=5mm είναι F=3,2 10-14 Ν, δηλαδή 36 x 1014 φορές μεγαλύτερη του βάρους. To συμπέρασμα αυτό, ότι το βάρος είναι αμελητέο συγκρινόμενο με την ηλεκτρική δύναμη, ισχύει και για τα άλλα στοιχειώδη σωματίδια -πρωτόνια, πυρήνες, ιόντα- όταν κινούνται μέσα στο ηλεκτρικό πεδίο.
|
|
ΠΑΡΑΔΕΙΓΜΑ 5-7 |
|||||||||||||||||||||||||||||||||
Δέσμη ηλεκτρονίων επιταχύνεται από την ηρεμία από διαφορά δυναμικού V0. Στη συνέχεια μπαίνει σε ομογενές ηλεκτρικό πεδίο που σχηματίζεται ανάμεσα σε δυο φορτισμένες πλάκες (πλακίδια απόκλισης) κάθετα στις δυναμικές γραμμές του πεδίου. Η διαφορά δυναμικού ανάμεσα στις πλάκες είναι V και η μεταξύ τους απόσταση d. To μήκος των πλακών είναι L. Τα ηλεκτρόνια βγαίνοντας από το ομογενές πεδίο προσκρούουν σε φθορίζουσα οθόνη που είναι τοποθετημένη κάθετα στην αρχική διεύθυνση κίνησης. Η οθόνη απέχει απόσταση D από τα πλακίδια απόκλισης. Η όλη διάταξη βρίσκεται μέσα σ’ ένα σωλήνα υψηλού κενού ώστε να αποφεύγονται οι συγκρούσεις των ηλεκτρονίων με τα μόρια του αέρα. Να βρεθεί η θέση στην οποία θα πέσει η δέσμη πάνω στη φθορίζουσα οθόνη. Δίνονται το στοιχειώδες φορτίο e και η μάζα του ηλεκτρονίου me.
Σχ. 5.28 Απάντηση:Τα ηλεκτρόνια επιταχυνόµενα από τη διαφορά δυναµικού V0 αποκτούν κινητική ενέργεια που δίνεται από το θεώρηµα έργου - ενέργειας.
Η κίνηση των ηλεκτρονίων μέσα στο ηλεκτρικό πεδίο που δημιουργούν τα πλακίδια απόκλισης, μελετήθηκε στην προηγούμενη παράγραφο. Όταν τα ηλεκτρόνια εξέλθουν από τα πλακίδια απόκλισης θα έχουν εκτραπεί από την αρχική τους πορεία κατά y1. H απόκλιση αυτή υπολογίστηκε στην (5.36) επομένως
Η γωνία που σχηματίζει η ταχύτητα εξόδου των ηλεκτρονίων με την αρχική διεύθυνση κίνησης, επίσης υπολογίστηκε από τη σχέση
Τα ηλεκτρόνια βγαίνοντας από το ομογενές πεδίο των πλακιδίων κινούνται ευθύγραμμα ομαλά με υ1. Μεγεθύνοντας την περιοχή εξόδου (Σχ. 5.29) βλέπουμε ότι σχηματίζεται ένα ορθογώνιο τρίγωνο με κάθετες πλευρές τις D και y2 και υποτείνουσα την τροχιά των ηλεκτρονίων. Ισχύει
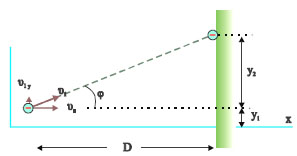 Σχ. 5.29 Σχ. 5.29
Αντικαθιστώντας την (5.40) βρίσκουμε
Η θέση της δέσμης στην οθόνη απέχει απόσταση y1+y2 από την αρχική διεύθυνση της δέσμης. Από τις (5.38), (3,39) και (5.41) βρίσκουμε:
|
Ο καθοδικός σωλήνας, (Σχ. 5.30), είναι ένας γυάλινος "σωλήνας" το εσωτερικό του οποίου βρίσκεται σε υψηλό κενό. H λειτουργία του στηρίζεται σε τρεις διαδοχικές διατάξεις. Η πρώτη ονομάζεται τηλεβόλο ηλεκτρονίων και είναι υπεύθυνη για την παραγωγή, επιτάχυνση και εστίαση μιας δέσμης ηλεκτρονίων. Η δεύτερη είναι ένας συνδυασμός ομογενών πεδίων. Μεταβάλλοντας την ένταση των πεδίων κατευθύνουμε τη δέσμη των ηλεκτρονίων. Η τρίτη είναι η οθόνη στην οποία παρατηρούμε τη θέση όπου προσπίπτουν τα ηλεκτρόνια. Ο σωλήνας απέναντι από το τηλεβόλο είναι επιστρωμένος με ειδικό υλικό που έχει την ιδιότητα να φθορίζει, δηλαδή να εκπέμπει φως, όταν πάνω του προσπίπτουν σωματίδια με μεγάλη ταχύτητα. Πάνω σ΄ αυτό το τμήμα του σωλήνα, που αποτελεί την οθόνη, πέφτουν με μεγάλη ταχύτητα τα ηλεκτρόνια της δέσμης. Στο σημείο στο οποίο πέφτουν τα ηλεκτρόνια η οθόνη φθορίζει έντονα και δημιουργείται μια φωτεινή κηλίδα.
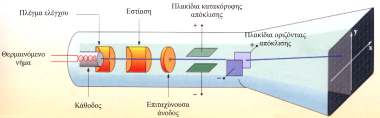 Σχ. 5.30 Σχ. 5.30
Στο αριστερό άκρο του σχήματος 3.30 φαίνεται το τηλεβόλο. Τα ηλεκτρόνια παράγονται εκεί με τη θέρμανση ενός μεταλλικού νήματος (κάθοδος). Θερμαίνοντας ένα μέταλλο δίνουμε σε κάποια από τα ελεύθερα ηλεκτρόνιά του κινητική ενέργεια αρκετή για να το εγκαταλείψουν. Στη συνέχεια τα ηλεκτρόνια επιταχύνονται από το ηλεκτρικό πεδίο που δημιουργείται ανάμεσα στην κάθοδο και σε ένα άλλο ηλεκτρόδιο (άνοδος). Η άνοδος βρίσκεται σε δυναμικό υψηλότερο από το δυναμικό της καθόδου και φέρει οπή. Τα περισσότερα ηλεκτρόνια που επιταχύνονται προς την άνοδο προσκρούουν σ΄ αυτή. Όσα από αυτά περνάνε από την οπή σχηματίζουν δέσμη και κινούνται προς την οθόνη με την οριζόντια ταχύτητα που απέκτησαν. Η διαφορά δυναμικού μεταξύ ανόδου και καθόδου είναι μερικά kV. Έτσι, η ταχύτητα που αποκτούν τα ηλεκτρόνια είναι της τάξεως των 107 m/s.
Στο τηλεβόλο, υπάρχουν διατάξεις που επιτρέπουν τον έλεγχο του αριθμού των ηλεκτρονίων που κατευθύνονται προς την οθόνη και την εστίαση της δέσμης.
Το εσωτερικό του καθοδικού σωλήνα βρίσκεται σε υψηλό κενό (περίπoυ 10-7 atm). Έτσι ελαχιστοποιούνται οι κρούσεις των ηλεκτρονίων της δέσμης με τα μόρια του αέρα που περιέχονται σ’ αυτόν. |
 Εικ. 5.3 Τηλεβόλο ηλεκτρονίων. Εικ. 5.3 Τηλεβόλο ηλεκτρονίων. |
 Εικ. 5.4 Παλμογράφος. Εικ. 5.4 Παλμογράφος.
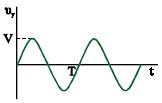 Σχ. 5.31 Εναλλασσόμενη τάση. Σχ. 5.31 Εναλλασσόμενη τάση.
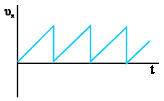 Σχ. 5.32 Πριονωτή τάση. Σχ. 5.32 Πριονωτή τάση. |
Η δέσμη των ηλεκτρονίων διέρχεται στη συνέχεια ανάμεσα από δύο ζεύγη μεταλλικών πλακιδίων (πλακίδια απόκλισης). Στο ένα ζεύγος τα μεταλλικά πλακίδια είναι οριζόντια και το ηλεκτρικό πεδίο που δημιουργείται ανάμεσά τους εκτρέπει τη δέσμη των ηλεκτρονίων κατακόρυφα. Το άλλο ζεύγος πλακιδίων είναι κατακόρυφο και εκτρέπει τη δέσμη των ηλεκτρονίων οριζόντια. Οι σχέσεις (5.39), (5.41) δείχνουν ότι η απόκλιση είναι ανάλογη της διαφοράς δυναμικού που εφαρμόζεται μεταξύ των πλακιδίων. Έτσι το σημείο της οθόνης στο οποίο προσπίπτει η δέσμη εξαρτάται από τις τάσεις που εφαρμόζουμε σε κάθε χρονική στιγμή στα δύο ζεύγη πλακιδίων. Εάν η διαφορά δυναμικού και στα δύο ζεύγη πλακιδίων απόκλισης είναι μηδενική τα ηλεκτρόνια της δέσμης κινούνται χωρίς να αποκλίνουν από την ευθύγραμμη τροχιά τους και προσκρούουν στο κέντρο της οθόνης.
Μετά την έξοδο από τα πεδία των πλακιδίων απόκλισης και μέχρι την πρόσκρουση στη φθορίζουσα οθόνη τα ηλεκτρόνια κινούνται ευθύγραμμα ομαλά.
Ο καθοδικός σωλήνας αποτελεί το βασικό στοιχείο του παλμογράφου. Πιο σύνθετες παραλλαγές του, πάνω όμως στην ίδια αρχή λειτουργίας, αποτελούν οι οθόνες της τηλεόρασης και του υπολογιστή.
Μια ειδική εφαρμογή του καθοδικού σωλήνα είναι ο παλμογράφος. Το κύριο στοιχείο ενός παλμογράφου είναι ένας καθοδικός σωλήνας του οποίου η οθόνη είναι βαθμολογημένη ώστε να μας επιτρέπει να κάνουμε μετρήσεις. Εξωτερικά ο παλμογράφος είναι ένα κουτί με μια οθόνη στην μπροστινή πλευρά και διάφορους ρυθμιστές (κουμπιά). Με τους ρυθμιστές υπάρχει η δυνατότητα:
Εάν μεταξύ των πλακιδίων κατακόρυφης εκτροπής εφαρμόσουμε μια τάση που μεταβάλλεται με τον χρόνο, έστω μια τάση της μορφής υy=V ημωt (εναλλασσόμενη τάση) (Σχ. 5.31) και στα πλακίδια οριζόντιας εκτροπής δεν εφαρμόζεται τάση η φωτεινή κηλίδα θα κινείται πάνω- κάτω σύμφωνα με τις αυξομειώσεις της υy. Για εναλλασσόμενες τάσεις όπως αυτή του δικτύου της ΔΕΗ η κηλίδα κινείται τόσο γρήγορα (50 φορές το δευτερόλεπτο) ώστε το μάτι να τη βλέπει σαν μια κατακόρυφη γραμμή.
Τάση σάρωσης
Εάν μεταξύ των πλακιδίων οριζόντιας εκτροπής εφαρμόσουμε τάση υx η οποία αυξάνεται γραμμικά και στη συνέχεια ελαττώνεται απότομα (πριονωτή τάση Σχ. 5.32) η κηλίδα στην οθόνη θα κινείται οριζόντια και ισοταχώς από τα αριστερά προς τα δεξιά και θα επιστρέφει απότομα πίσω, για |
να ξαναρχίσει πάλι την ίδια κίνηση. Αυτή η παλινδρομική οριζόντια κίνηση της κηλίδας ονομάζεται σάρωση της οθόνης. Την τάση σάρωσης την εφαρμόζει ο ίδιος ο παλμογράφος και υπάρχει δυνατότητα ρύθμισης της συχνότητα της υx ώστε να επιτυγχάνουμε γρήγορη ή αργή σάρωση.
Μερικές από τις πιο απλές χρήσεις του παλμογράφου είναι.
α) Μέτρηση συνεχούς τάσεως
Απενεργοποιούμε την τάση σάρωσης και εφαρμόζουμε την τάση V που θέλουμε να μετρήσουμε στα πλακίδια κατακόρυφης απόκλισης. Η κηλίδα αποκλίνει κατακόρυφα (Σχ. 5.33α). Από την απόσταση της κηλίδας από το κέντρο της οθόνης μπορούμε να βρούμε την εφαρμοζόμενη συνεχή τάση V.
β) Μέτρηση εναλλασσόμενης τάσης
Απενεργοποιούμε την τάση σάρωσης και στα πλακίδια κατακόρυφης απόκλισης εφαρμόζουμε τάση της μορφής υy=Vημωt (εναλλασσόμενη τάση) (Σχ. 5.31). Η κηλίδα θα ανεβοκατεβαίνει γρήγορα κατακόρυφα και στην οθόνη του παλμογράφου θα σχηματιστεί μια κατακόρυφη γραμμή (Σχ. 5.33β). Από το μήκος της γραμμής μπορούμε να υπολογίσουμε το V (πλάτος της εναλλασσόμενης τάσης). Συγκεκριμένα το μήκος της γραμμής είναι ανάλογο του 2V.

γ) Μελέτη κυματομορφών
Εφαρμόζουμε ταυτόχρονα τη υx (τάση σάρωσης), στα πλακίδια οριζόντιας απόκλισης και τη υy (εναλλασσόμενη) στα πλακίδια κατακόρυφης απόκλισης. Αυτό που προκύπτει στην οθόνη είναι μια κυματοειδής γραμμή (Εικ. 5.5) που ονομάζεται κυματομορφή της τάσης υy. Μπορούμε έτσι να παρακολουθήσουμε στην οθόνη του παλμογράφου και να μελετήσουμε τάσεις που μεταβάλλονται με το χρόνο, όπως η εναλλασσόμενη αλλά και πιο σύνθετες.
Επειδή τα ηλεκτρόνια έχουν πολύ μικρή μάζα, η απόκλιση της δέσμης των ηλεκτρονίων στον καθοδικό σωλήνα συμβαίνει σχεδόν ακαριαία και ο παλμογράφος έχει τη δυνατότητα να δείξει πολύ γρήγορες μεταβολές στην τάση. |
Σχ. 5.33 (α) Συνεχής τάση V εφαρμόζεται στα πλακίδια κατακόρυφης απόκλισης, η απόσταση d της κηλίδας από το κέντρο της οθόνης είναι ανάλογη της τάση V. β) Εναλλασσόμενη τάση εφαρμόζεται στα πλακίδια κατακόρυφης απόκλισης, το μήκος της γραμμής στην οθόνη είναι ανάλογο του διπλάσιου πλάτους της εναλλασσόμενης τάσης.
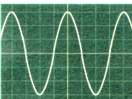 Σχ. 5.33 Η κυματομορφή μιας εναλλασσόμενης τάσης όπως φαίνεται στην οθόνη του παλμογράφου. Σχ. 5.33 Η κυματομορφή μιας εναλλασσόμενης τάσης όπως φαίνεται στην οθόνη του παλμογράφου. |