| ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ | 5 |
 |
|
 Εικ. 5.1 Michael Faraday (1791-1867). Άγγλος. O πατέρας του ήταν φτωχός σιδεράς. Η εκπαίδευσή του ήταν στοιχειώδης. Σε ηλικία δεκατριών χρόνων δούλευε ως βοηθός βιβλιοδέτη. Ο Michael δε βιβλιοδετούσε απλώς τα βιβλία, τα διάβαζε κιόλας. Αργότερα, ως γραμματέας του Davy γνώρισε τους μεγαλύτερους φυσικούς της εποχής του. Ήταν βαθύτατα θρησκευόμενος. Η επιστημονική του δραστηριότητα ήταν τεράστια. Μέχρι το τέλος της ζωής του οι σημειώσεις του περιείχαν δεκαέξι χιλιάδες καταχωρίσεις, που καθαρόγραφε και βιβλιοδετούσε προσεκτικά μόνος του. Ήταν εξαιρετικός πειραματικός φυσικός. Στον Faraday οφείλουμε τη θεμελίωση του ηλεκτρισμού με τη σύγχρονη μορφή. Εικ. 5.1 Michael Faraday (1791-1867). Άγγλος. O πατέρας του ήταν φτωχός σιδεράς. Η εκπαίδευσή του ήταν στοιχειώδης. Σε ηλικία δεκατριών χρόνων δούλευε ως βοηθός βιβλιοδέτη. Ο Michael δε βιβλιοδετούσε απλώς τα βιβλία, τα διάβαζε κιόλας. Αργότερα, ως γραμματέας του Davy γνώρισε τους μεγαλύτερους φυσικούς της εποχής του. Ήταν βαθύτατα θρησκευόμενος. Η επιστημονική του δραστηριότητα ήταν τεράστια. Μέχρι το τέλος της ζωής του οι σημειώσεις του περιείχαν δεκαέξι χιλιάδες καταχωρίσεις, που καθαρόγραφε και βιβλιοδετούσε προσεκτικά μόνος του. Ήταν εξαιρετικός πειραματικός φυσικός. Στον Faraday οφείλουμε τη θεμελίωση του ηλεκτρισμού με τη σύγχρονη μορφή.
|
5-1 ΕΙΣΑΓΩΓΗ
Στο προηγούμενο κεφάλαιο είδαμε ότι το ηλεκτρικό ρεύμα συνεπάγεται τη δημιουργία μαγνητικού πεδίου. Στα 1831 ο Άγγλος ερευνητής Michael Faraday (Φαραντέι) μελέτησε το ενδεχόμενο η ύπαρξη μαγνητικού πεδίου να δημιουργεί σ’ ένα κλειστό κύκλωμα ηλεκτρικό ρεύμα. Μια σειρά από πειράματα τον οδήγησαν στο συμπέρασμα ότι ένα σταθερό μαγνητικό πεδίο δε δημιουργεί ηλεκτρικό ρεύμα. Αντίθετα, αν μεταβληθεί η μαγνητική ροή που διέρχεται από την επιφάνεια που ορίζει το κύκλωμα, στο κύκλωμα εμφανίζεται ένα απροσδόκητο ρεύμα. Στα ίδια συμπεράσματα κατέληξε την ίδια χρονιά, ανεξάρτητα από τον Faraday, ο Αμερικανός Joseph Henry (Χένρι). Η σημασία του φαινομένου, που ονομάζεται ηλεκτρομαγνητική επαγωγή, είναι πελώρια στο σύγχρονο κόσμο. Αρκεί να αναφέρουμε ότι η παραγωγή και μεταφορά ηλεκτρικής ενέργειας στηρίζεται σ’ αυτό. Λέγεται ότι όταν τον ρώτησε ένας πολιτικός πόσο χρήσιμες είναι οι ανακαλύψεις του, ο Faraday απάντησε: « Προς το παρόν δε γνωρίζω, αλλά μια μέρα θα μπορέσετε να τις φορολογήσετε ».
 Εικ. 5.2 Ηλεκτρογεννήτριες υδροηλεκτρικού σταθμού. Η παραγωγή ηλεκτρικής ενέργειας στηρίζεται στο φαινόμενο της επαγωγής.
5-2 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
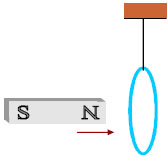
Πρώτο. Συνδέουμε τα άκρα ενός πηνίου με ένα «γαλβανόμετρο του μηδενός» ώστε να δημιουργηθεί κλειστό κύκλωμα. Τα γαλβανόμετρα είναι ευαίσθητα όργανα που μας επιτρέπουν να μετράμε μικρές εντάσεις ρεύματος. Στο γαλβανόμετρο που χρησιμοποιούμε, το μηδέν βρίσκεται στο μέσον της κλίμακας. Ο δείκτης του, ανάλογα με τη φορά του ρεύματος αποκλίνει προς τη μια ή την άλλη πλευρά του μηδενός. Πλησιάζουμε στο πηνίο ένα ραβδόμορφο μαγνήτη, έτσι ώστε ο άξονάς του να ταυτίζεται με τον άξονα του πηνίου. Κατά τη διάρκεια της κίνησης του μαγνήτη το |
γαλβανόμετρο δείχνει ότι το κύκλωμα διαρρέεται από ρεύμα, αν και δεν έχουμε καμιά πηγή
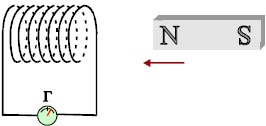 Σχ. 5.1 Όταν υπάρχει σχετική κίνηση του μαγνήτη ως προς το πηνίο το γαλβανόμετρο δείχνει ρεύμα Σχ. 5.1 Όταν υπάρχει σχετική κίνηση του μαγνήτη ως προς το πηνίο το γαλβανόμετρο δείχνει ρεύμα
Όταν ο μαγνήτης σταματήσει να κινείται το ρεύμα μηδενίζεται. Αν απομακρύνουμε το μαγνήτη το γαλβανόμετρο δείχνει ότι πάλι το κύκλωμα διαρρέεται από ρεύμα, αντίθετης φοράς τώρα σε σχέση με πριν. Μια ακόμη παρατήρηση είναι ότι η απόκλιση του γαλβανομέτρου, άρα η ένταση του ηλεκτρικού ρεύματος, εξαρτάται από το πόσο γρήγορα πλησιάζουμε ή απομακρύνουμε το μαγνήτη.
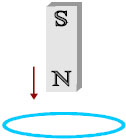
Δεύτερο. Συνδέουμε τα άκρα αγώγιμου πλαισίου σε γαλβανόμετρο έτσι ώστε να δημιουργείται κλειστό κύκλωμα. Εισάγουμε το πλαίσιο στο χώρο ενός ισχυρού ομογενούς μαγνητικού πεδίου που δημιουργείται ανάμεσα στους πόλους ενός ηλεκτρομαγνήτη. Κατά τη διάρκεια της εισόδου (αν το επίπεδο του πλαισίου δεν είναι παράλληλο στις δυναμικές γραμμές), το γαλβανόμετρο δείχνει ρεύμα. Όταν το πλαίσιο βρεθεί να κινείται εξολοκλήρου εντός του πεδίου το ρεύμα μηδενίζεται. Κατά τη διάρκεια της εξόδου του πλαισίου από το πεδίο εμφανίζεται πάλι ρεύμα στο πλαίσιο αντίθετης φοράς από πριν. Και εδώ η ένταση του ρεύματος είναι μεγαλύτερη αν η είσοδος και η έξοδος γίνουν γρηγορότερα.
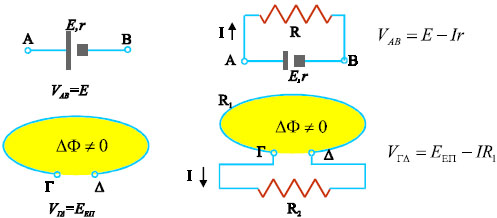
Αυτό που συνέβη στη διάρκεια των δυο αυτών πειραμάτων ήταν ότι μεταβλήθηκε η μαγνητική ροή από την επιφάνεια που ορίζεται από τις σπείρες του πηνίου στην πρώτη περίπτωση, από τις σπείρες του πλαισίου στη δεύτερη. Σε αυτή τη μεταβολή πρέπει να αναζητήσουμε την αιτία της δημιουργίας του ηλεκτρικού ρεύματος. Αν σε κάποια από τις προηγούμενες περιπτώσεις το κύκλωμα ήταν ανοιχτό, δε θα υπήρχε ρεύμα. Ωστόσο, κατά τη διάρκεια μεταβολής της μαγνητικής ροής, στα ανοιχτά άκρα του κυκλώματος -του πηνίου ή του πλαισίου- θα εμφανιζόταν τάση. Η τάση αυτή ονομάζεται τάση από επαγωγή.
Θα πρέπει να σημειωθεί ότι για την εμφάνιση αυτής της τάσης δεν είναι αναγκαίο να υπάρχει πηνίο ή πλαίσιο πολλών σπειρών. Αρκεί να μεταβληθεί η μαγνητική ροή που διέρχεται από την επιφάνεια που ορίζει ο αγωγός. Τότε, κατά τη διάρκεια της μεταβολής, εμφανίζεται στα άκρα του αγωγού τάση από επαγωγή (σχ. 5.3).
Το φαινόμενο της εμφάνισης τάσης στα άκρα κάποιου αγωγού, εξαιτίας της μεταβολής της μαγνητικής ροής που διέρχεται από την επιφάνεια που ορίζει, ονομάζεται ηλεκτρομαγνητική επαγωγή.
|
 Eικ. 5.3 Πειραματική επίδειξη δημιουργίας ρεύματος σε κλειστό κύκλωμα εξαιτίας της κίνησης ενός μαγνήτη. Eικ. 5.3 Πειραματική επίδειξη δημιουργίας ρεύματος σε κλειστό κύκλωμα εξαιτίας της κίνησης ενός μαγνήτη. 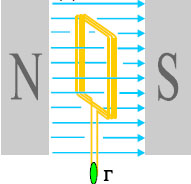 Σχ. 5.2 Κατά την είσοδο του πλαισίου στο μαγνητικό πεδίο, το γαλβανόμετρο δείχνει ότι το πλαίσιο διαρρέεται από ρεύμα. Σχ. 5.2 Κατά την είσοδο του πλαισίου στο μαγνητικό πεδίο, το γαλβανόμετρο δείχνει ότι το πλαίσιο διαρρέεται από ρεύμα.
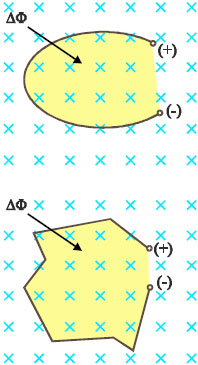 Σχ. 5.3 Όταν μεταβάλλεται η μαγνητική ροή που διέρχεται από την επιφάνεια που ορίζει ένας αγωγός με το σχήμα του, στα άκρα του αγωγού εμφανίζεται τάση από επαγωγή. Τα πρόσημα + και - στο σχήμα είναι αυθαίρετα. Σχ. 5.3 Όταν μεταβάλλεται η μαγνητική ροή που διέρχεται από την επιφάνεια που ορίζει ένας αγωγός με το σχήμα του, στα άκρα του αγωγού εμφανίζεται τάση από επαγωγή. Τα πρόσημα + και - στο σχήμα είναι αυθαίρετα. |
|
Ο νόμος που διέπει το φαινόμενο, ονομάζεται νόμος της επαγωγής ή νόμος του Faraday και διατυπώνεται ως εξής:
Η ηλεκτρεγερτική δύναμη που επάγεται σε ένα κύκλωμα είναι ίση με το ρυθμό μεταβολής της μαγνητικής ροής που διέρχεται από την επιφάνεια που ορίζει το κύκλωμα.
Αν το κύκλωμα αποτελείται από Ν σπείρες και ΔΦΒ είναι η μεταβολή της μαγνητικής ροής σε κάθε σπείρα, ο νόμος της επαγωγής γράφεται
Παρατηρήσεις
|
ΠΑΡΑΔΕΙΓΜΑ 5.1 |
Κλειστό συρμάτινο κυκλικό πλαίσιο βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με το επίπεδό του κάθετο στις δυναμικές γραμμές του πεδίου. Κάποια στιγμή το μαγνητικό πεδίο αρχίζει να αυξάνεται με σταθερό ρυθμό και από την τιμή Β1=0,1Τ γίνεται Β2=0,5Τ σε χρόνο Δt=0,2s. Το πλαίσιο αποτελείται από Ν=100σπείρες. Το εμβαδόν κάθε σπείρας είναι Α=4x10-2 m2. Η αντίσταση του πλαισίου είναι R=20Ω. Να υπολογιστούν: α) Η ηλεκτρεγερτική δύναμη που επάγεται στο πλαίσιο β) Η ένταση του ρεύματος που διαρρέει το πλαίσιο κατά τη διάρκεια του φαινομένου. γ) Το ηλεκτρικό φορτίο που διέρχεται από μια τομή του σύρματος κατά τη διάρκεια του φαινομένου.
Απάντηση:
Αντικαθιστώντας στην (5.1.) βρίσκουμε ΕΕΠ = 8V
από όπου προκύπτει I = 0,4A
όπου Δt ο χρόνος που διαρκεί το φαινόμενο.
Παρόλο που τα στοιχεία που γνωρίζουμε επαρκούν για να υπολογιστεί το φορτίο από τη σχέση (5.3) αξίζει να αντικαταστήσουμε το ρεύμα από τη σχέση (5.2) οπότε η (5.3) γίνεται
Αν στη σχέση αυτή αντικαταστήσουμε την ηλεκτρεγερτική δύναμη από την (5.1) προκύπτει
και τελικά βρίσκουμε ΔQ = 0,08C Παρατηρήστε ότι το συνολικό φορτίο που μετακινείται είναι ανεξάρτητο της χρονικής διάρκειας του φαινομένου. |
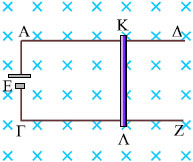
 Σχ. 5.5 Ο αγωγός ΚΛ κινείται μέσα σε ομογενές μαγνητικό πεδίο. Σχ. 5.5 Ο αγωγός ΚΛ κινείται μέσα σε ομογενές μαγνητικό πεδίο.
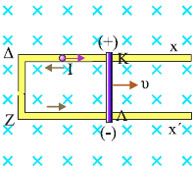 Σχ. 5.6 Ο αγωγός ΚΛ ολισθαίνει πάνω στους ακίνητους αγωγούς xΔΖx΄. Όλο το σύστημα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο. Η συσσώρευση φορτίου στα άκρα του αγωγού ΚΛ, προκαλεί κίνηση φορτίου στους ακίνητους αγωγούς. Σχ. 5.6 Ο αγωγός ΚΛ ολισθαίνει πάνω στους ακίνητους αγωγούς xΔΖx΄. Όλο το σύστημα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο. Η συσσώρευση φορτίου στα άκρα του αγωγού ΚΛ, προκαλεί κίνηση φορτίου στους ακίνητους αγωγούς. |
5-3 ΕΥΘΥΓΡΑΜΜΟΣ ΑΓΩΓΟΣ ΚΙΝΟΥΜΕΝΟΣ
ΟΜΟΓΕΝΕΣ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ
Αν και τα πειράματα επιβεβαιώνουν πλήρως το νόμο Faraday απομένει αδιευκρίνιστο το πώς δημιουργούνται τα επαγωγικά ρεύματα. Το παρακάτω παράδειγμα φωτίζει κάπως τα πράγματα.
Ευθύγραμμος αγωγός μήκους L κινείται με σταθερή ταχύτητα υ κάθετα στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου Β (σχ. 5.5). Τα ελεύθερα ηλεκτρόνιά του, συμμετέχοντας στην κίνηση του αγωγού, κινούνται και αυτά με ταχύτητα υ κάθετα στις δυναμικές γραμμές του πεδίου. Ένα ελεύθερο ηλεκτρόνιο επειδή κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο θα δεχτεί δύναμη Lorentz
Τότε παύει η μετακίνηση φορτίου και το σημείο Κ βρίσκεται σε υψηλότερο δυναμικό από το Λ. Η διαφορά δυναμικού VΚΛ μεταξύ των άκρων του αγωγού Κ και Λ υπολογίζεται από
VΚΛ= BυL. Πρόκειται για μια διαφορά δυναμικού που οφείλεται στη δράση του μαγνητικού πεδίου (επάγεται από το μαγνητικό πεδίο).
Ας θεωρήσουμε τον ίδιο ακριβώς αγωγό να κάνει την ίδια κίνηση μέσα στο ίδιο πεδίο. Τώρα όμως τα άκρα του αγωγού ολισθαίνουν πάνω στους ακίνητους αγωγούς xΔΖx΄ (σχ. 5.6). Η συσσώρευση φορτίου, στα άκρα του αγωγού ΚΛ, που οφείλεται στην κίνησή του, προκαλεί την κίνηση φορτίου στο τμήμα ΚΔΖΛ των ακίνητων αγωγών. Ας φανταστούμε ένα ελεύθερο ηλεκτρόνιο των αγωγών ΚΔΖΛ. Το ηλεκτρόνιο θα κινηθεί προς το σημείο Κ, διαταράσσοντας προς στιγμήν την ισορροπία των φορτίων στα άκρα Κ και Λ. Μια νέα μετακίνηση φορτίου μέσα στον αγωγό ΚΛ θα αποκαταστήσει την ισορροπία. Το ίδιο θα συμβεί με κάθε ηλεκτρόνιο που φτάνει στο σημείο Κ, δηλαδή ο αγωγός ΚΛ, λειτουργεί ως αντλία φορτίου, ως ηλεκτρική πηγή, ηλεκτρεγερτικής δύναμης BυL.
Αν ένας ευθύγραμμος αγωγός κινείται με ταχύτητα υ, μέσα σε ομογενές μαγνητικό πεδίο, έτσι ώστε ο αγωγός, η ταχύτητα και το μαγνητικό πεδίο να είναι κάθετα ανά δύο μεταξύ τους, στον αγωγό αναπτύσσεται ηλεκτρεγερτική δύναμη από επαγωγή
|
|||||||||||
Στο ίδιο αποτέλεσμα καταλήγουμε με το νόμο του Faraday. Ας επανέλθουμε στον αγωγό ΚΛ που ολισθαίνει πάνω στους ακίνητους αγωγούς xΔΖx΄.
Ο αγωγός που κινείται και οι ακίνητοι αγωγοί σχηματίζουν ένα κλειστό πλαίσιο σχήματος ορθογωνίου παραλληλογράμμου με αυξανόμενο εμβαδόν Α. Σύμφωνα με το νόμο του Faraday, στο πλαίσιο θα αναπτυχθεί ΗΕΔ από επαγωγή
Βέβαια στην περίπτωση ενός ευθύγραμμου αγωγού που κινείται μέσα στο
Θα μπορούσαμε λοιπόν να πούμε ότι ηλεκτρομαγνητική επαγωγή είναι το φαινόμενο της εμφάνισης τάσης στα άκρα αγωγών όταν μεταβάλλεται η μαγνητική ροή που διέρχεται από την επιφάνεια που ορίζουν με το σχήμα τους ή όταν από την επιφάνεια που ορίζουν με την κίνησή τους διέρχεται μαγνητική ροή. |
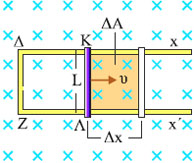 Σχ. 5.8 Καθώς ο αγωγός ΚΛ κινείται, μεταβάλλεται το εμβαδόν του πλαισίου ΚΔΖΛ, με αποτέλεσμα να μεταβάλλεται η μαγνητική ροή που διέρχεται από αυτό. Σχ. 5.8 Καθώς ο αγωγός ΚΛ κινείται, μεταβάλλεται το εμβαδόν του πλαισίου ΚΔΖΛ, με αποτέλεσμα να μεταβάλλεται η μαγνητική ροή που διέρχεται από αυτό.
|
ΠΑΡΑΔΕΙΓΜΑ 5.2
Αγωγός ΑΓ με μήκος l=0,4m κινείται με ταχύτητα υ=5m/s, χωρίς τριβές, πάνω στους παράλληλους αγωγούς Δx και Ζx΄, μένοντας διαρκώς κάθετος και σε επαφή με αυτούς. Τα άκρα Δ και Ζ αγωγών συνδέονται μεταξύ τους με σύρμα αντίστασης R=5Ω. Η αντίσταση όλων των άλλων αγωγών είναι αμελητέα. Η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο Β=0,5Τ κάθετο στο επίπεδο που ορίζουν οι αγωγοί. Να βρεθεί η δύναμη που απαιτείται για να διατηρηθεί ισοταχής η κίνηση του αγωγού ΑΓ.
Απάντηση:
Επομένως, στο άκρο Γ σωρεύεται αρνητικό φορτίο και στο Α θετικό (σχ. 5.9)
Η φορά του ρεύματος είναι αυτή του σχήματος.
Επειδή ο αγωγός ΑΓ διαρρέεται από ρεύμα, δέχεται από το μαγνητικό πεδίο δύναμη Laplace.
|
|
ΠΑΡΑΔΕΙΓΜΑ 5.3
Απάντηση: Τη στιγμή μηδέν (σχ. 5.12α) που κλείσαμε το διακόπτη, ο αγωγός ΚΛ ήταν ακίνητος. Μοναδική ηλεκτρεγερτική
φορά του φαίνεται στο σχήμα 5.12α. Επειδή ο αγωγός ΚΛ διαρρέεται από ρεύμα, δέχεται από το μαγνητικό πεδίο δύναμη Laplace FL = BIl
ομόρροπη με τη δύναμη (σχ. 5.12α).
|
||||||||||||||||||||||||
|
5-4 Ο ΚΑΝΟΝΑΣ ΤΟΥ LENZ ΚΑΙ Η ΑΡΧΗ
ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΣΤΟ ΦΑΙΝΟΜΕΝΟ ΤΗΣ ΕΠΑΓΩΓΗΣ
Ο Lenz (Λέντς) διατύπωσε ένα κανόνα που δίνει τη φορά του ρεύματος από επαγωγή. Σύμφωνα με τον κανόνα αυτό
τα επαγωγικά ρεύματα έχουν τέτοια φορά ώστε να αντιτίθενται στο αίτιο που τα προκαλεί |
Παίρνοντας υπόψη τον κανόνα του Lenz, που προσδιορίζει τη φορά του επαγωγικού ρεύματος, άρα και την πολικότητα της επαγωγικής τάσης, γράφουμε τη σχέση (5.1) που εκφράζει το νόμο της επαγωγής με τη μορφή:
Ο κανόνας του Lenz αποτελεί συνέπεια της αρχής διατήρησης της ενέργειας. Στα δύο παραδείγματα που ακολουθούν θα δούμε πώς εφαρμόζεται ο κανόνας του Lenz και γιατί η φορά του ρεύματος που ορίζει είναι συνέπεια της αρχής διατήρησης της ενέργειας.
Για να υπερνικηθεί η άπωση που δέχεται ο μαγνήτης από το πηνίο δαπανάται ενέργεια, που μετατρέπεται σε θερμότητα στους αγωγούς. Αν το πηνίο διαρρεόταν από
Σύμφωνα με τον κανόνα του Lenz η φορά του ρεύματος πρέπει να είναι τέτοια ώστε να αντιτίθεται στην αιτία που το προκάλεσε, δηλαδή στην κίνηση του αγωγού ΚΛ. Το ρεύμα πρέπει να έχει τέτοια φορά ώστε ή δύναμη Laplace που ασκείται στον αγωγό να αντιτίθεται στην κίνησή του. Για να διατηρείται η κίνηση του αγωγού ισοταχής, είναι αναγκαίο να ασκείται σε αυτόν δύναμη F, αντίθετη με τη δύναμη Laplace. Mέσω της δύναμης αυτής προσφέρεται στο κύκλωμα ενέργεια. Αν το ρεύμα είχε αντίθετη φορά, το μαγνητικό |
|
|
πεδίο θα ασκούσε στον αγωγό δύναμη ίδιας κατεύθυνσης με την ταχύτητά του. Στην περίπτωση αυτή δεν απαιτείται ενέργεια για να διατηρηθεί η κίνηση του αγωγού και στο κύκλωμα θα παραγόταν διαρκώς ηλεκτρική ενέργεια που θα μετατρεπόταν σε θερμότητα στην αντίσταση R. Όμως, σύμφωνα με την αρχή διατήρησης της ενέργειας είναι αδύνατη η παραγωγή μιας μορφής ενέργειας χωρίς αντίστοιχη δαπάνη άλλης μορφής ενέργειας.
Η αρχή διατήρησης της ενέργειας στο φαινόμενο της επαγωγής
Εάν το κύκλωμα παρουσιάζει συνολικά αντίσταση θα διαρρέεται από ρεύμα
Σε χρονικό διάστημα Δt, το ρεύμα, λόγω φαινομένου Joule, θα αποδώσει στο περιβάλλον θερμότητα
Για να διατηρούμε την κίνηση του αγωγού ΚΛ ισοταχή πρέπει να ασκούμε εξωτερική δύναμη F, αντίθετη της δύναμης Laplace που δέχεται ο ΚΛ.
Στο χρονικό διάστημα Δt ο αγωγός μετατοπίζεται κατά Δt = υΔt και το έργο της F στο ίδιο χρονικό διάστημα θα είναι
Βλέπουμε ότι χρειάστηκε να προσφέρουμε έργο ίσο με τη θερμότητα που παράχθηκε. |
5-5 ΣΤΡΕΦΟΜΕΝΟΣ ΑΓΩΓΟΣ
ΔΦ να βάλουμε τη ροή που περνάει από την επιφάνεια που ορίζει με την κίνησή του ο αγωγός στον αντίστοιχο χρόνο. Στην περίπτωση που εξετάζουμε θα ισχύει:
με τον οποίο σαρώνεται η επιφάνεια είναι σταθερός αφού η γωνιακή ταχύτητα περιστροφής είναι σταθερή. Έτσι μπορούμε να γράψουμε ότι
|
|
Σχ. 5.18 Το πλαίσιο στρέφεται με σταθερή γωνιακή ταχύτητα ω μέσα σε ομογενές μαγνητικό πεδίο. |
όπου πL2 το εμβαδόν της επιφάνειας που ορίζει ο αγωγός σε μια πλήρη περιστροφή και Τ η περίοδος περιστροφής του.
και με βάση την (5.7) η (5.6), δίνει
ΣΤΡΕΦΟΜΕΝΟΣ ΔΙΣΚΟΣ
Θεωρούμε αγώγιμο δίσκο με ακτίνα r, του οποίου το επίπεδο είναι κάθετο στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου. Στρέφουμε το δίσκο με σταθερή γωνιακή ταχύτητα ω γύρω από άξονα που περνάει από το κέντρο του και είναι παράλληλος στις δυναμικές γραμμές. Αν θεωρήσουμε ότι ο δίσκος αποτελείται από ένα μεγάλο αριθμό αγωγών σαν αυτόν της προηγούμενης παραγράφου, τότε ανάμεσα
Μπορούμε να χρησιμοποιήσουμε αυτή τη συσκευή ως πηγή σταθερής τάσης αν τη συμπληρώσουμε με ολισθαίνουσες επαφές (ψήκτρες) όπως στο σχήμα 5.17. Η πολικότητα της ΗΕΔ που αναπτύσσεται από επαγωγή εξαρτάται από τη φορά περιστροφής του δίσκου. Στην περίπτωση του σχήματος τα σημεία της περιφέρειας του δίσκου βρίσκονται σε υψηλότερο δυναμικό από το κέντρο. Η συσκευή ονομάζεται δίσκος του Faraday.
5-6 ΣΤΡΕΦΟΜΕΝΟ ΠΛΑΙΣΙΟ – ΕΝΑΛΛΑΣΣΟΜΕΝΗ
ΤΑΣΗ
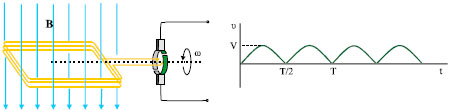
Ένα αγώγιμο πλαίσιο σχήματος ορθογωνίου παραλληλογράμμου και εμβαδού Α στρέφεται με σταθερή γωνιακή ταχύτητα ω μέσα σε ομογενές μαγνητικό πεδίο γύρω από άξονα που είναι κάθετος στις δυναμικές γραμμές του πεδίου και βρίσκεται στο επίπεδό του.
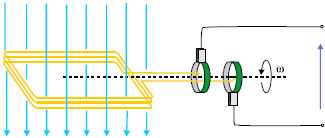
Αν τη χρονική στιγμή t = 0 το επίπεδο του πλαισίου είναι κάθετο στο Β σε μία τυχαία χρονική στιγμή t το πλαίσιο θα έχει στραφεί κατά γωνία θ = ωt και η μαγνητική ροή μέσα από την επιφάνεια του πλαισίου θα είναι ΦB= BAσυν ωt. Καθώς το πλαίσιο στρέφεται η μαγνητική ροή μέσα από |
την επιφάνειά του μεταβάλλεται και κατά συνέπεια στο πλαίσιο εμφανίζεται ηλεκτρεγερτική δύναμη από επαγωγή. Από το νόμο του Faraday προκύπτει:
Εάν το πλαίσιό μας έχει Ν σπείρες τότε
Η τάση αυτή, που πιο συχνά γράφεται με τη μορφή
όπου V = ΝωBA,
είναι ημιτονοειδής συνάρτηση του χρόνου (σχ. 5.19) και ονομάζεται εναλλασσόμενη τάση (ac) γιατί η πολικότητά της εναλλάσσεται, στο χρόνο μιας περιστροφής του πλαισίου.
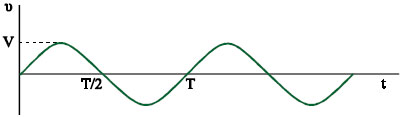
Παντού η μεταφορά και διανομή της ηλεκτρικής ενέργειας γίνεται με εναλλασσόμενη τάση. Στην Ελλάδα, στα δίκτυα των πόλεων το πλάτος της 1 Το αποτέλεσμα προέκυψε από την παραγώγιση της μαγνητικής ροής ως προς το χρόνο. |
|
|||||||||||||||||||||||||||||||||||||||||||||
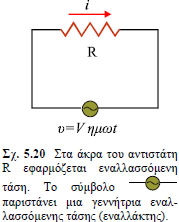
Σχ. 5.21 Το εναλλασσόμενο ρεύμα μεταβάλλεται ημιτονοειδώς με το χρόνο.
|
εναλλασσόμενης τάσης, στην κατανάλωση, είναι f = 50 Hz.
5-7 ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ
Στα άκρα ενός αντιστάτη εφαρμόζουμε εναλλασσόμενη τάση με μια γεννήτρια εναλλασσόμενης τάσης. Η τάση αυτή εξαναγκάζει τα ελεύθερα ηλεκτρόνια στους αγωγούς να κάνουν ταλάντωση με συχνότητα τη συχνότητα της εναλλασσόμενης τάσης που εφαρμόσαμε. Η ένταση του ρεύματος που διαρρέει το κύκλωμα κάποια στιγμή είναι
όπου το Ι είναι η μέγιστη τιμή της έντασης του ρεύματος (πλάτος) και δίνεται από τη
Το ρεύμα αυτό, που η φορά του μεταβάλλεται περιοδικά με το χρόνο, ονομάζεται εναλλασσόμενο ρεύμα. Στο σχήμα 5.21 παριστάνεται γραφικά η ένταση του εναλλασσόμενου ρεύματος σε συνάρτηση με το χρόνο. Με το σύμβολο θα συμβολίζουμε ρεύματα που μεταβάλλονται με το χρόνο. 
Η γωνία ωt ονομάζεται φάση και το ω γωνιακή συχνότητα του εναλλασσόμενου ρεύματος. Η εναλλασσόμενη τάση που εφαρμόσαμε στα άκρα του αντιστάτη και το ρεύμα παίρνουν ταυτόχρονα τη μέγιστη ή την ελάχιστη τιμή. Λέμε ότι τα δύο μεγέθη βρίσκονται σε φάση (ή ότι η διαφορά φάσης τους είναι μηδέν). Καθώς οι φορείς του ηλεκτρικού φορτίου μέσα στους αγωγούς του κυκλώματος ταλαντώνονται, προσκρούουν στα ιόντα του πλέγματος και χάνουν την ενέργειά που τους παρέχει για την κίνησή τους η πηγή. Η ενέργεια αυτή αποδίδεται υπό μορφή θερμότητας στο περιβάλλον. Παρουσιάζεται κι εδώ, όπως και στα κυκλώματα συνεχούς ρεύματος, το φαινόμενο Joule. |
ΠΑΡΑΔΕΙΓΜΑ 5.4 |
Αντιστάτης με R=20Ω, συνδέεται στο δίκτυο της ΔΕΗ. Όπως γνωρίζετε η τάση που παρέχει το δίκτυο της ΔΕΗ έχει πλάτος
Απάντηση:
|
|||||||||||||||
5-8 ΕΝΕΡΓΟΣ ΕΝΤΑΣΗ – ΕΝΕΡΓΟΣ ΤΑΣΗ
Επειδή το εναλλασσόμενο ρεύμα και η εναλλασσόμενη τάση διαρκώς μεταβάλλονται, το να γνωρίζουμε τι τιμή έχουν ορισμένη στιγμή ελάχιστη πρακτική αξία έχει. Για το λόγο αυτό, στηριζόμενοι στο θερμικό φαινόμενο που προκαλούν σε ένα αντιστάτη, ορίζουμε τις ενεργές τους τιμές, που είναι μεγέθη σταθερά.
Αποδεικνύεται ότι το και το πλάτος Ιεν του εναλλασσομένου ρεύματος συνδέονται με τη σχέση
Ενεργός τάση Vεν μιας εναλλασσόμενης τάσης, είναι η τιμή της συνεχούς τάσης, που αν εφαρμοστεί στα άκρα αντιστάτη ( R ), προκαλεί συνεχές ρεύμα έντασης ίσης με την ενεργό ένταση του εναλλασσόμενου ρεύματος που θα προκαλούσε η εναλλασσόμενη τάση στον ίδιο αντιστάτη. |
|
|
Αποδεικνύεται ότι η ενεργός τάση και το πλάτος V της εναλλασσόμενης τάσης συνδέονται με τη σχέση
Όταν λέμε ότι οι ρευματοδότες στα σπίτια μας δίνουν 220 V, ή ότι κάποια συσκευή δουλεύει στα 220 V, 16 Α, αναφερόμαστε σε ενεργές τιμές. Τα όργανα που χρησιμοποιούμε για τη μέτρηση εναλλασσόμενων τάσεων και ρευμάτων δείχνουν ενεργές τιμές.
5-9 O ΝΟΜΟΣ ΤΟΥ JOULE (ΤΖΑΟΥΛ) - ΙΣΧΥΣ ΤΟΥ
ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ
Μπορούμε να χρησιμοποιήσουμε αυτή τη συσκευή ως πηγή σταθερής τάσης αν τη συμπληρώσουμε με ολισθαίνουσες επαφές (ψήκτρες) όπως στο σχήμα 5.17. Η πολικότητα της ΗΕΔ που αναπτύσσεται από επαγωγή εξαρτάται από τη φορά περιστροφής του δίσκου. Στην περίπτωση του σχήματος τα σημεία της περιφέρειας του δίσκου βρίσκονται σε υψηλότερο δυναμικό από το κέντρο. Η συσκευή ονομάζεται δίσκος του Faraday.
Η ισχύς του εναλλασσομένου ρεύματος (ο ρυθμός με τον οποίο το εναλλασσόμενο ρεύμα μεταφέρει στο κύκλωμα ενέργεια κάθε στιγμή) δίνεται από τη σχέση
Επειδή η ένταση του ρεύματος μεταβάλλεται διαρκώς, η ισχύς δεν έχει σταθερή τιμή. Για να τονίσουμε ότι η ισχύς μεταβάλλεται με το χρόνο ονομάζουμε την ισχύ αυτή στιγμιαία ισχύ.
Η στιγμιαία ισχύς έχει ελάχιστη πρακτική αξία. Στην πράξη χρησιμοποιείται η μέση ισχύς, η οποία είναι σταθερή. Είναι η ισχύς που κατά μέσο όρο καταναλώνεται στο κύκλώμα. Η μέση ισχύς ορίζεται ως εξής:
Μέση ισχύς P ονομάζεται το πηλίκο της ενέργειας που μεταφέρει το ηλεκτρικό ρεύμα στο κύκλωμα σε χρόνο μιας περιόδου προς το χρόνο αυτό
Η μέση ισχύς σε ένα αντιστάτη ισούται με
|
ΠΑΡΑΔΕΙΓΜΑ 5.5 |
Αγωγός που έχει αντίσταση R=8Ω συνδέεται σε εναλλασσόμενη τάση ενεργού τιμής Vεν=16V. Nα υπολογιστεί το ποσό θερμότητας που αποδίδει ο αγωγός στο περιβάλλον σε χρόνο t=10min.
Απάντηση:
|
|||||||||||||||
5-10 ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΗΣ ΚΑΙ
ΣΥΝΕΧΟΥΣ ΤΑΣΗΣ
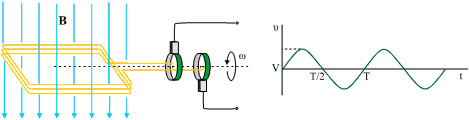
Στην παράγραφο (5-6) μελετήσαμε μια διάταξη πλαισίου στρεφόμενου μέσα σε ομογενές μαγνητικό πεδίο που παράγει εναλλασσόμενη τάση. Πρόκειται για το πρότυπο της γεννήτριας εναλλασσόμενης τάσης, που λέγεται και εναλλακτήρας. Η παραγόμενη τάση αναπτύσσεται στο εξωτερικό κύκλωμα με τη βοήθεια δύο δακτυλίων επαφής (σχ. 5.23) οι οποίοι περιστρέφονται με το πλαίσιο. Σταθερές επαφές, που ονομάζονται ψήκτρες, ολισθαίνουν στους δακτυλίους και αποτελούν την έξοδο του εναλλακτήρα.
|
Σχ. 5.23 Αρχή λειτουργίας γεννήτριας εναλλασσόμενης τάσης (εναλλακτήρας).
|
 Εικ. 5.5 Δυναμό (εσωτερικό). Εικ. 5.5 Δυναμό (εσωτερικό).  Εικ. 5.6 Ρότορας. Εικ. 5.6 Ρότορας.Εικ. 5.7 Η ηλεκτρική ενέργεια μεταφέρεται από τα εργοστάσια παραγωγής στην κατανάλωση με αγωγούς μεταφοράς υπό υψηλή τάση.
Σχ. 5.25 Διάγραμμα μετατροπής της μηχανικής ενέργειας σε ηλεκτρική
 Εικ. 5.7Το πλαίσιο στρέφεται με σταθερή γωνιακή ταχύτητα ω μέσα σε ομογενές μαγνητικό πεδίο. Εικ. 5.7Το πλαίσιο στρέφεται με σταθερή γωνιακή ταχύτητα ω μέσα σε ομογενές μαγνητικό πεδίο. |
 Σχ. 5.24 Η αρχή λειτουργίας του δυναμό ενός ποδηλάτου Σχ. 5.24 Η αρχή λειτουργίας του δυναμό ενός ποδηλάτου
Στα εργοστάσια παραγωγής ενέργειας ο μαγνήτης έχει αντικατασταθεί από έναν ηλεκτρομαγνήτη. Ο ρότορας δηλαδή είναι ένα πηνίο που διαρρέεται από συνεχές ρεύμα και τίθεται σε περιστροφική κίνηση με τη βοήθεια ενός στροβίλου (τουρμπίνα). Ο στρόβιλος τίθεται σε κίνηση με διάφορους τρόπους. Σ’ ένα υδροηλεκτρικό εργοστάσιο εκμεταλλευόμαστε τη μηχανική ενέργεια μιας υδατόπτωσης για να κινήσουμε το στρόβιλο κι έτσι τη μετατρέπουμε σε ηλεκτρική (σχ. 5.25). Σ’ ένα θερμοηλεκτρικό εργοστάσιο με την καύση λιγνίτη θερμαίνουμε νερό, ο ατμός που παράγεται όταν εκτονώνεται, με κατάλληλες διατάξεις, πάλι κινεί το στρόβιλο κ.ο.κ

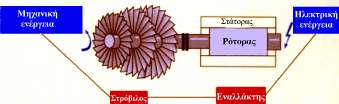
Στο σχήμα 5.26 φαίνεται η αρχή λειτουργίας μιας πηγής που δίνει συνεχή (όχι σταθερή) τάση. Εδώ, αντί για δυο ανεξάρτητους δακτυλίους, όπως στον εναλλακτήρα, τα άκρα του πλαισίου είναι συνδεδεμένα με δύο ημιδακτυλίους που περιστρέφονται μαζί με το πλαίσιο. Η διάταξη αυτή λέγεται συλλέκτης. Τη στιγμή που η τάση αλλάζει |
πολικότητα οι συνδέσεις με το εξωτερικό κύκλωμα αντιστρέφονται και η τάση που παίρνουμε είναι συνεχής (σχ. 5.26).
5-11 ΑΝΟΡΘΩΣΗ ΕΝΑΛΛΑΣΣΟΜΕΝΗΣ ΤΑΣΗΣ
Η εναλλασσόμενη τάση παρουσιάζει πλεονεκτήματα έναντι της συνεχούς. Όμως, πολλές συσκευές καθημερινής χρήσης χρειάζονται συνεχή τάση -και μάλιστα σταθερή- για να λειτουργήσουν. Τη μετατροπή μιας εναλλασσόμενης τάσης σε συνεχή και στη συνέχεια σε σταθερή την επιτυγχάνουμε με το συνδυασμό δύο διατάξεων, του ανορθωτή και του εξομαλυντή. Στον ανορθωτή χρησιμοποιούμε διόδους. Η δίοδος είναι μία διάταξη που επιτρέπει στο ρεύμα να τη διαρρέει κατά τη μία φορά εύκολα ενώ πρακτικά δε διαρρέεται από ρεύμα κατά την αντίθετη φορά. Η δίοδος παριστάνεται με το σύμβολο
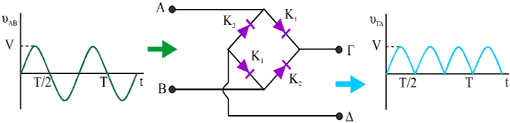
Η συνεχής τάση που παίρνουμε με τη διάταξη αυτή ονομάζεται μερικώς ανορθωμένη (ημιανορθωμένη). Στο σχήμα (5.28) βλέπουμε ένα κύκλωμα το οποίο με ένα συνδυασμό διόδων μετατρέπει την εναλλασσόμενη τάση υΑΒ της εισόδου, σε συνεχή τάση υΓΔ στην έξοδο. Η τάση αυτή ονομάζεται πλήρως ανορθωμένη.
Ο εξομαλυντής αποτελείται από ένα πυκνωτή και ένα αντιστάτη συνδεδεμένους παράλληλα. Λόγω της δυσκολίας που παρουσιάζει το κύκλωμα να παρακολουθήσει τις |
Σχ. 5.27 Διάταξη ανόρθωσης της εναλλασσόμενης τάσης. Η εναλ-λασσόμενη τάση υΑΒ στην είσοδο του κυκλώματος μετατρέπεται σε συνεχή υΓΔ στην έξοδο.
Σχ. 5.28 Διάταξη με τέσσερις διόδους που μετατρέπει την εναλλασσόμενη τάση σε πλήρως ανορθωμένη. Κατά τη μία ημιπερίοδο της τάσης εισόδου όταν το σημείο Α είναι σε ψηλότερο δυναμικό από το σημείο Β, άγουν οι δίοδοι Κ1, ενώ κατά την άλλη ημιπερίοδο άγουν οι δίοδοι Κ2. |
Σχ. 5.29 Με τον εξομαλυντή, η πλήρως ανορθωμένη τάση μετα-τρέπεται σε τάση σχεδόν σταθερή.
 Σχ. 5.30 Το ορθογώνιο πλαίσιο που διαρρέεται από ρεύμα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο. Το ζεύγος δυνάμεων Laplace που ασκούνται στο πλαίσιο το στρέφουν. Σχ. 5.30 Το ορθογώνιο πλαίσιο που διαρρέεται από ρεύμα βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο. Το ζεύγος δυνάμεων Laplace που ασκούνται στο πλαίσιο το στρέφουν.
|
γρήγορες μεταβολές της τάσεως μας δίνει στην έξοδό του τάσεις σχεδόν σταθερές. Αν τροφοδοτήσουμε την είσοδό του με πλήρως ανορθωμένη τάση, καθώς η τάση εισόδου αυξάνεται ο πυκνωτής φορτίζεται και όταν η τάση εισόδου πάρει τη μέγιστη τιμή της το φορτίο του πυκνωτή γίνεται μέγιστο. Στη συνέχεια, καθώς η τάση εισόδου μειώνεται, ο πυκνωτής εκφορτίζεται μέσω του αντιστάτη. Ο χρόνος που διαρκεί η εκφόρτιση του πυκνωτή εξαρτάται από τις τιμές της αντίστασης και της χωρητικότητας. Ο χρόνος εκφόρτισης αυξάνεται όταν οι τιμές τους είναι μεγάλες. Στο κύκλωμα εξομάλυνσης οι τιμές των R και C είναι μεγάλες. Έτσι η τάση στον πυκνωτή, άρα και η τάση εξόδου (VΓΔ), μειώνεται πολύ πιο αργά από την τάση εισόδου. Όταν η τάση στην είσοδο -καθώς αυξάνεται πάλι- γίνει ίση με την τάση στους οπλισμούς του πυκνωτή αρχίζει εκ νέου να αυξάνεται το φορτίο του. Το φαινόμενο επαναλαμβάνεται όταν η τάση γίνει μέγιστη. Με κατάλληλη επιλογή των στοιχείων που συνθέτουν τον ανορθωτή μπορούμε να επιτύχουμε τάσεις κατά ικανοποιητική προσέγγιση σταθερές. 
5-12 Ο ΗΛΕΚΤΡΟΚΙΝΗΤΗΡΑΣ
Οι ηλεκτρικοί κινητήρες είναι διατάξεις που μετατρέπουν την ηλεκτρική ενέργεια σε μηχανική. Δηλαδή ένας ηλεκτροκινητήρας είναι μια αντίστροφη ηλεκτρογεννήτρια.
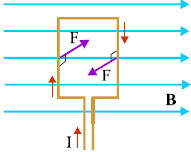
Αρχή λειτουργίας Τοποθετούμε ένα ορθογώνιο πλαίσιο στο εσωτερικό ενός ομογενούς μαγνητικού πεδίου. Συνδέουμε στα άκρα του μια πηγή συνεχούς τάσης V, οπότε το πλαίσιο διαρρέεται από ρεύμα. Στις πλευρές του πλαισίου θα ασκούνται δυνάμεις Laplace, όπως δείχνει το σχήμα 5.30. Το ζεύγος των δυνάμεων στρέφει το πλαίσιο. Συνδέοντας το πλαίσιο μ’ έναν άξονα μπορούμε να εκμεταλλευτούμε την περιστροφική του κίνηση. Περιγραφή πραγματικού ηλεκτροκινητήρα
Στους ηλεκτροκινητήρες δεν υπάρχει μόνο ένα ρευματοφόρο πλαίσιο αλλά πολλά. Τα πλαίσια αυτά είναι τοποθετημένα πάνω σε ένα κύλινδρο από μαλακό σίδηρο, το ρότορα. Ο ρότορας μπορεί να στρέφεται γύρω από τον άξονά του (σχ. 5.31). Στην επιφάνειά του και κατά μήκος του άξονά του φέρει αύλακες. Στους αύλακες περιτυλίγονται χάλκινοι μονωμένοι αγωγοί, έτσι ώστε να δημιουργείται μια σειρά από πλαίσια. Οι άκρες όλων αυτών των πλαισίων καταλήγουν σε ένα κύλινδρο, το συλλέκτη. Ο συλλέκτης χωρίζεται σε τμήματα, μονωμένα μεταξύ τους, κάθε ένα από τα οποία είναι σε ηλεκτρική επαφή με ένα πλαίσιο. Δύο ακίνητες ψήκτρες από γραφίτη που μπορούν να συνδεθούν με πηγή τάσης V, εφάπτονται στο συλλέκτη. |
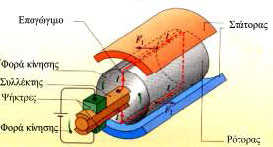
Ο ρότορας περιβάλλεται από ένα σταθερό τμήμα, το στάτορα, που φέρει μόνιμους μαγνήτες (στους μικρούς κινητήρες) ή ηλεκτρομαγνήτες (στους μεγάλους). Ο στάτορας δημιουργεί μαγνητικό πεδίο κάθετο στον άξονα του ρότορα.
Όταν ο κινητήρας ρευματοδοτηθεί, ένα από τα πλαίσια που είναι τυλιγμένα στο ρότορα, αυτό που εκείνη τη στιγμή είναι σε επαφή με τις ψήκτρες, διαρρέεται από ρεύμα. Το μαγνητικό πεδίο ασκεί σ’ αυτό ζεύγος δυνάμεων και το στρέφει. Μαζί στέφεται και ολόκληρος ο ρότορας. Με τη στροφή χάνεται η επαφή του πλαισίου αυτού με τις ψήκτρες και διακόπτεται το ρεύμα, ένα άλλο πλαίσιο όμως παίρνει τη θέση του και, έχοντας επαφή με τις ψήκτρες, για τον ίδιο λόγο στρέφεται κι΄ αυτό. Στη συνέχεια ένα άλλο παίρνει τη θέση του κ.ο.κ έτσι διατηρείται η κίνηση του ρότορα. που βρίσκεται μέσα σε μαγνητικό πεδίο.
Οι ηλεκτροκινητήρες έχουν απόδοση από 50%, οι μικροί, έως 90% οι μεγάλοι. Οι χρήσεις τους είναι απεριόριστες. Τα ηλεκτρικά κατσαβίδια, τα μίξερ και η μίζα του αυτοκινήτου, οι ανελκυστήρες, τα τρόλεϊ και το μετρό λειτουργούν με ηλεκτροκινητήρες.
5-13 ΑΜΟΙΒΑΙΑ ΕΠΑΓΩΓΗ
Σύμφωνα με το νόμο του Faraday σ’ ένα ακίνητο κύκλωμα επάγεται μια ηλεκτρεγερτική δύναμη εάν μεταβάλλεται η μαγνητική ροή που διέρχεται από το κύκλωμα. Τη μεταβολή της μαγνητικής ροής μπορούμε να την πετύχουμε με τη βοήθεια ενός δεύτερου κυκλώματος στο οποίο μεταβάλλουμε την ένταση του ρεύματος. Λέμε τότε ότι τα δύο κυκλώματα βρίσκονται σε επαγωγική σύζευξη. |
Σχ. 5.31 Ηλεκτροκινητήρας (αρχή λειτουργίας).
 Εικ. 5.9 Μίζα αυτοκινήτου (εκκινητήρας). Εικ. 5.9 Μίζα αυτοκινήτου (εκκινητήρας).
|
Σχ. 5.32 Το πηνίο Α διαρρέεται από ρεύμα μεταβλητής έντασης. Το μαγνητικό πεδίο που δημι-ουργεί το πηνίο Α μεταβάλλεται, με αποτέλεσμα να μεταβάλλεται η μαγνητική ροή που διέρχεται από το πηνίο Β και να δημιουργείται σ΄ αυτό ηλεκτρεγερτική δύναμη από επαγωγή.
 Εικ. 5.10 Μετασχηματιστής. Η λειτουργία του στηρίζεται στο φαινόμενο της αμοιβαίας επαγω-γής. Η τάση που εφαρμόζεται στο ένα πηνίο μετασχηματίζεται σε μια άλλη τάση διαφορετικού πλάτους στο δεύτε-ρο πηνίο. Εικ. 5.10 Μετασχηματιστής. Η λειτουργία του στηρίζεται στο φαινόμενο της αμοιβαίας επαγω-γής. Η τάση που εφαρμόζεται στο ένα πηνίο μετασχηματίζεται σε μια άλλη τάση διαφορετικού πλάτους στο δεύτε-ρο πηνίο.
|
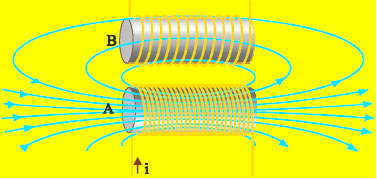
Η εμφάνιση ηλεκτρεγερτικής δύναμης σ’ ένα κύκλωμα, εξαιτίας της μεταβολής του ρεύματος που συμβαίνει σ’ ένα άλλο κύκλωμα, λέγεται αμοιβαία επαγωγή.
μπορεί να πάρει τη μορφή
Το Μ ονομάζεται συντελεστής αμοιβαίας επαγωγής των κυκλωμάτων.
Σύμφωνα με τη σχέση (5.9),
η ηλεκτρεγερτική δύναμη από αμοιβαία επαγωγή που αναπτύσσεται σε ένα κύκλωμα Β εξαιτίας μεταβολής της έντασης του ρεύματος σε ένα κύκλωμα Α, είναι ανάλογη του ρυθμού με τον οποίο μεταβάλλεται το ρεύμα στο κύκλωμα Α.
Το φαινόμενο της αμοιβαίας επαγωγής είναι έντονο στην περίπτωση δύο πηνίων με κοινό άξονα.
Ο συντελεστής αμοιβαίας επαγωγής δύο πηνίων εξαρτάται από τα γεωμετρικά τους χαρακτηριστικά, τη σχετική τους θέση και το υλικό του πυρήνα τους. |
Υπολογισμός συντελεστή αμοιβαίας επαγωγής δύο πηνίων Θα υπολογίσουμε το συντελεστή αμοιβαίας επαγωγής δυο πηνίων στην ειδική περίπτωση που έχουν κοινό άξονα, όπως στο σχήμα 5.33. Τα πηνία έχουν, αντίστοιχα, Ν1 και Ν2 σπείρες και είναι τοποθετημένα έτσι ώστε να έχουν κοινό άξονα, με το πηνίο 1 να περικλείει το πηνίο 2. Το πηνίο 1 διαρρέεται από μεταβαλλόμενο ρεύμα i1 . Εάν τα πηνία δεν περιέχουν κάποιο σώμα στον πυρήνα η ένταση του μαγνητικού πεδίου που δημιουργείται στο εσωτερικό του πηνίου 1 -άρα και στο εσωτερικό του πηνίου 2- θα δίνεται από τη σχέση:
όπου μ0 η μαγνητική διαπερατότητα του κενού και n1 ο αριθμός σπειρών του πρώτου πηνίου ανά μονάδα μήκους. Η μαγνητική ροή σε κάθε σπείρα του πηνίου 2 θα είναι:
όπου Α το εμβαδόν της επιφάνειας στην οποία μεταβάλλεται η ροή Η επαγόμενη ηλεκτρεγερτική δύναμη στο πηνίο 2 θα είναι
όπου N2 ο αριθμός σπειρών του πηνίου 2
Το σταθερό γινόμενο N2 μ0n1Α, που θα το συμβολίζουμε με M21 εξαρτάται μόνο από τα γεωμετρικά στοιχεία των δύο πηνίων. Εάν τα πηνία είναι τυλιγμένα γύρω από πυρήνα από υλικό του οποίου η μαγνητική διαπερατότητα μ είναι σταθερή (ανεξάρτητη του B) τότε
Εάν επαναλάβουμε τη διαδικασία στην αντίθετη περίπτωση όπου ένα μεταβαλλόμενο ρεύμα i2 στο πηνίο 2 επάγει ΗΕΔ στο πηνίο 1 καταλήγουμε στη σχέση
Θα περίμενε κανείς τα M21 και M12 να είναι διαφορετικά επειδή τα δύο πηνία δεν είναι ίδια και γιατί η ροή που διέρχεται από αυτά δεν είναι ίδια. Όμως, τα M21 και M12 είναι πάντα ίσα και θα τα συμβολίζουμε με το σύμβολο M.
5-14 ΑΥΤΕΠΑΓΩΓΗ
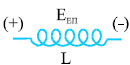
Το κύκλωμα του σχήματος 5.34 περιλαμβάνει πηγή, ρυθμιστική αντίσταση, λαμπτήρα, πηνίο και διακόπτη. Μετακινούμε το δρομέα στη ρυθμιστική αντίσταση ώστε ο λαμπτήρας μόλις να φωτοβολεί. Αν ανοίξουμε το διακόπτη Δ του κυκλώματος θα παρατηρήσουμε ότι για λίγο ο λαμπτήρας συνεχίζει να φωτοβολεί και μάλιστα, αμέσως μετά το άνοιγμα του διακόπτη, πιο έντονα από πριν. Αυτό συμβαίνει γιατί η απότομη μείωση της έντασης του ρεύματος που διαρρέει το πηνίο προκαλεί αντίστοιχη ελάττωση του μαγνητικού του πεδίου, επομένως και της μαγνητικής ροής που διέρχεται από τις σπείρες του. Η μεταβολή της μαγνητικής ροής στο πηνίο έχει ως αποτέλεσμα τη δημιουργία ηλεκτρεγερτικής δύναμης από επαγωγή στο πηνίο. Η ηλεκτρεγερτική δύναμη που δημιουργείται στο πηνίο όταν ανοίξουμε το διακόπτη, προκαλεί ρεύμα στο κύκλωμα πηνίο - λαμπτήρας και αναγκάζει το λαμπτήρα να φωτοβολήσει για λίγο. |
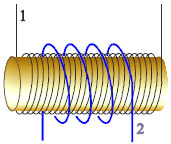 Σχ. 5.33 Τα δύο πηνία έχουν κοινό άξονα. Σχ. 5.33 Τα δύο πηνία έχουν κοινό άξονα.
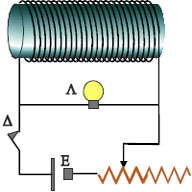 Σχ. 5.34 Αν ανοίξουμε το διακόπτη θα παρατηρήσουμε ότι ο λαμπτήρας εξακολουθεί να φωτοβολεί για λίγο χρόνο. Σχ. 5.34 Αν ανοίξουμε το διακόπτη θα παρατηρήσουμε ότι ο λαμπτήρας εξακολουθεί να φωτοβολεί για λίγο χρόνο. |
Σχ. 5.35 Η ηλεκτρεγερτική δύναμη από αυτεπαγωγή αντιτίθε-ται στη μεταβολή της έντασης του ρεύματος.
Σχ. 5.30 Μετά το κλείσιμο του διακόπτη το ρεύμα καθυστερεί να πάρει την τελική του τιμή.
|
Ηλεκτρεγερτική δύναμη δημιουργείται στο πηνίο και κάθε φορά που στο κύκλωμα (όσο ο διακόπτης είναι κλειστός) μεταβάλλουμε το ρεύμα που το διαρρέει. Ηλεκτρεγερτική δύναμη επαγωγικής προέλευσης δημιουργείται σε κάθε κύκλωμα στο οποίο μεταβάλλεται η ένταση του ρεύματος, συνήθως όμως τη μελετάμε στα πηνία γιατί εκεί το φαινόμενο είναι εντονότερο. Το φαινόμενο ονομάζεται αυτεπαγωγή.
Αυτεπαγωγή ονομάζεται το φαινόμενο κατά το οποίο δημιουργείται ηλεκτρεγερτική δύναμη σε ένα κύκλωμα, όταν μεταβάλλεται το ρεύμα που το διαρρέει. Η ηλεκτρεγερτική δύναμη που δημιουργείται ονομάζεται ηλεκτρεγερτική δύναμη από αυτεπαγωγή (ΕAYT).
Αν το ρεύμα που διαρρέει ένα πηνίο αυξάνεται, σύμφωνα με τον κανόνα του Lenz, στο πηνίο δημιουργείται ηλεκτρεγερτική δύναμη που παρεμποδίζει την αύξηση του ρεύματος. Αν το ρεύμα στο πηνίο μειώνεται, η ηλεκτρεγερτική δύναμη που δημιουργείται έχει την τάση να το διατηρήσει σταθερό.
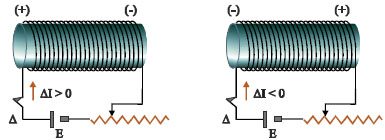
Το πηνίο αντιδρά σε κάθε μεταβολή της έντασης του ρεύματος που το διαρρέει.
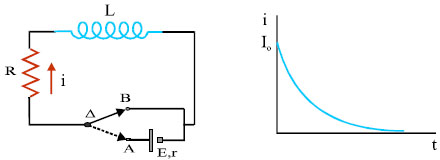
Η αυτεπαγωγή είναι ιδιότητα των κυκλωμάτων αντίστοιχη με την αδράνεια των σωμάτων. Τα σώματα αντιστέκονται στη μεταβολή της ταχύτητάς τους. Τα κυκλώματα αντιστέκονται στη μεταβολή του ρεύματος που τα διαρρέει. Μέτρο της αδράνειας των σωμάτων είναι η μάζα τους. Μέτρο της αδράνειας των κυκλωμάτων είναι ο συντελεστής αυτεπαγωγής τους. Στο σχήμα 5.36 το κύκλωμα περιλαμβάνει πηγή, διακόπτη, αντιστάτη και πηνίο. Αν κλείσουμε το διακόπτη, το κύκλωμα αρχίζει να διαρρέεται από ρεύμα, επειδή όμως το πηνίο αντιδρά στην αύξηση του ρεύματος, το ρεύμα καθυστερεί να πάρει την τελική του τιμή Ιο.
Στο σχήμα 5.37 ο μεταγωγός αρχικά είναι στη θέση Α και το κύκλωμα διαρρέεται από σταθερό ρεύμα Ιο. Τη στιγμή μηδέν, ο μεταγωγός τοποθετείται στη |
θέση Β. Το κύκλωμα συνεχίζει για λίγο χρόνο να διαρρέεται από ρεύμα. Το πηνίο, αντιδρώντας στη μείωση του ρεύματος δημιουργεί ηλεκτρεγερτική δύναμη που δίνει για μικρό χρόνο ρεύμα ίδιας φορά με το αρχικό ρεύμα.
Ο νόμος της αυτεπαγωγής
Το φαινόμενο της αυτεπαγωγής αποτελεί μια ειδική περίπτωση του
στην περίπτωση της αυτεπαγωγής
Ο συντελεστής αναλογίας L ονομάζεται συντελεστής αυτεπαγωγής ή αυτεπαγωγή. Το (-) στη σχέση είναι συνέπεια του κανόνα του Lenz.
Από τη σχέση (5.10), που αποτελεί ειδική έκφραση του νόμου της επαγωγής, προκύπτει ότι
η ηλεκτρεγερτική δύναμη από αυτεπαγωγή σε ένα κύκλωμα είναι ανάλογημε το ρυθμό μεταβολής της έντασης του ρεύματος που το διαρρέει.
Η σχέση (5.10) δίνει τη μέση ηλεκτρεγερτική δύναμη από αυτεπαγωγή. Για να βρούμε την τιμή της μια χρονική στιγμή πρέπει ο χρόνος Δt να είναι απειροστά μικρός.
Από τη σχέση (5.10) παρατηρούμε ότι ο συντελεστής αυτεπαγωγής ενός πηνίου, είναι αριθμητικά ίσος με την ηλεκτρεγερτική δύναμη που επάγεται στο πηνίο, όταν το ρεύμα μεταβάλλεται με ρυθμό 1A/s.
Ο συντελεστής αυτεπαγωγής ενός πηνίου εξαρτάται από τα γεωμετρικά χαρακτηριστικά του και από τη μαγνητική διαπερατότητα του υλικού που βρίσκεται στο εσωτερικό του. |
Σχ. 5.37 Η μετακίνηση του μεταγωγού από τη θέση Α στη θέση Β δε μηδενίζει αμέσως το ρεύμα στο κύκλωμα εξαιτίας της ηλεκτρεγερτικής δύναμης από αυτεπαγωγή που αναπτύσσεται στο πηνίο.
|
|
Ενεργειακή μελέτη
Στο πείραμα με το λαμπτήρα είπαμε ότι μετά το άνοιγμα του διακόπτη, ο λαμπτήρας, για λίγο χρόνο, συνεχίζει να φωτοβολεί. Αυτό δείχνει ότι στο κύκλωμα υπήρχε αποθηκευμένη ενέργεια, η οποία δόθηκε στο λαμπτήρα και προκάλεσε τη φωτοβολία του.
Αποδεικνύεται ότι ένα πηνίο που διαρρέεται από ρεύμα έχει αποθηκευμένη ενέργεια στο μαγνητικό του πεδίο
Υπολογισμός του συντελεστή αυτεπαγωγής πηνίου Το μαγνητικό πεδίο στο εσωτερικό ενός πηνίου που διαρρέεται από ρεύμα είναι
Από κάθε σπείρα του πηνίου περνάει μαγνητική ροή:
όπου Α το εμβαδόν της σπείρας του πηνίου Η ηλεκτρεγερτική δύναμη από αυτεπαγωγή στο πηνίο θα είναι
όπου ο αριθμός σπειρών του πηνίου.
εξαρτάται μόνο από τα γεωμετρικά στοιχεία του πηνίου.
Εάν τα πηνίο περιέχει πυρήνα από υλικό μαγνητικής διαπερατότητας μ, ο συντελεστής αυτεπαγωγής του θα είναι:
|
ΠΑΡΑΔΕΙΓΜΑ 5.6
γ) Πόση θερμότητα αποδίδεται στο περιβάλλον, από τη στιγμή που ο μεταγωγός τοποθετείται στη θέση Β μέχρι να μηδενιστεί το ρεύμα στο κύκλωμα; Δίνονται: ο συντελεστής αυτεπαγωγής του πηνίου L=0,1H, η ηλεκτρεγερτική δύναμη και η εσωτερική αντίσταση της πηγής Ε=20V, r =0 και η αντίσταση R=4Ω. Το πηνίο είναι ιδανικό (δηλαδή δεν έχει ωμική αντίσταση).
Απάντηση:
|
||||||||||||||||||||||||||||||||
ΣΥΝΟΨΗ |
||||||||||||||||||||||||||||||||||||||||||
Όταν μεταβάλλεται η μαγνητική ροή που διέρχεται από την επιφάνεια που ορίζει ένας αγωγός με το σχήμα του, στον αγωγό επάγεται ηλεκτρεγερτική δύναμη η οποία ισούται με το ρυθμό μεταβολής της μαγνητικής ροής.
Όταν ευθύγραμμος αγωγός μήκους L κινείται με σταθερή ταχύτητα υ (υ ⊥ L) σε επίπεδο κάθετο στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου Β, εμφανίζει ΗΕΔ από επαγωγή, ίση με
Σε ευθύγραμμο αγωγό μήκους L που στρέφεται με σταθερή γωνιακή ταχύτητα ω γύρω από άξονα, παράλληλο με τις δυναμικές γραμμές πεδίου Β, που περνάει από το ένα του άκρο, εμφανίζεται ΗΕΔ από επαγωγή ίση με
Τα επαγωγικά ρεύματα έχουν πάντα τέτοια φορά ώστε να αντιτίθενται στο αίτιο που τα προκαλεί. Στα άκρα στρεφόμενου πλαισίου Ν σπειρών, εμβαδού Α, που στρέφεται με σταθερή γωνιακή ταχύτητα ω γύρω από άξονα που βρίσκεται στο επίπεδό του και είναι κάθετος στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου Β αναπτύσσεται από επαγωγή του εναλλασσόμενη τάση.
Ενεργός ένταση εναλλασσόμενου ρεύματος είναι η σταθερή ένταση ρεύματος που θα προκαλούσε το ίδιο θερμικό αποτέλεσμα αν διέρρεε έναν ωμικό αγωγό για το ίδιο χρονικό διάστημα με το εναλλασσόμενο ρεύμα. Ενεργός τάση είναι εκείνη η σταθερή τάση που αν εφαρμοσθεί στα άκρα ενός αντιστάτη αυτός διαρρέεται από σταθερό ρεύμα έντασης ίσης με την ενεργό ένταση. Ηλεκτρογεννήτρια είναι διάταξη που μετατρέπει μηχανική ενέργεια σε ηλεκτρική. Η λειτουργία της βασίζεται στο φαινόμενο της επαγωγής. Οι ηλεκτρικοί κινητήρες είναι διατάξεις που μετατρέπουν την ηλεκτρική ενέργεια σε μηχανική. Το φαινόμενο της εμφάνισης ΗΕΔ από επαγωγή σ’ ένα κύκλωμα εξαιτίας της μεταβολής της έντασης του ρεύματος σ’ ένα άλλο κύκλωμα λέγεται αμοιβαία επαγωγή
όπου Μ ο συντελεστής αμοιβαίας επαγωγής των δύο κυκλωμάτων. Η επαγωγική ΗΕΔ που αναπτύσσεται σ’ ένα κύκλωμα λόγω της μεταβολής της έντασης του ρεύματος που το διαρρέει λέγεται ΗΕΔ από αυτεπαγωγή.
όπου L ο συντελεστής αυτεπαγωγής του κυκλώματος. |
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ |
1. Κατασκευάστε μια απλή γεννήτρια
2. Κατασκευάστε έναν απλό ηλεκτρικό κινητήρα
|
||||||||||||||||||||||||||||||||||||||||
ΕΡΩΤΗΣΕΙΣ |
 Σχ. 5.40 Σχ. 5.40 |
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
 Σχ. 5.46 Σχ. 5.46
 Σχ. 5.46 Σχ. 5.46 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 Σχ. 5.47 Σχ. 5.47
 Σχ. 5.49 Σχ. 5.49
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 Σχ. 5.50 Σχ. 5.50
|
||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||
ΑΣΚΗΣΕΙΣ |
 Σχ. 5.52 Σχ. 5.52 |
|
|||||||||||||||||||||||||||||||||
|
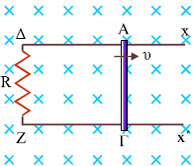 Σχ. 5.53 Σχ. 5.53
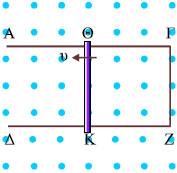 Σχ. 5.54 Σχ. 5.54 |
||||||||||||||||||||||||||||||||||||||||||||
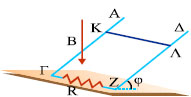 Σχ. 5.55 Σχ. 5.55
|
|
||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
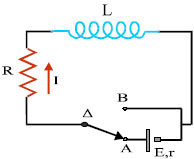 Σχ. 5.56 Σχ. 5.56 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ΠΡΟΒΛΗΜΑΤΑ |
|
|
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 Σχ. 5.57 Σχ. 5.57 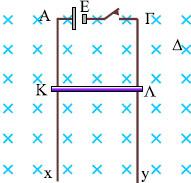 Σχ. 5.58 Σχ. 5.58 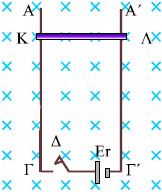 Σχ. 5.59 Σχ. 5.59 |
||||||||||||||||||||||||||||||||||||
 Σχ. 5.60 Σχ. 5.60
 Σχ. 5.61 Σχ. 5.61 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
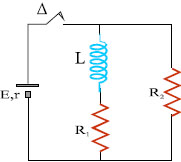 Σχ. 5.62 Σχ. 5.62
|
||||||||||||

 Εικ. 5.11 James Clerk Maxwell (1831-1879). Ο κορυφαίος θεωρητικός φυσικός του 19ου αιώνα. Θεμελιωτής της σύγχρονης ηλεκτρομαγνητικής θεωρίας και ένας από τους θεμελιωτές της Θερμοδυναμικής και της Στατιστικής μηχανικής. Γεννήθηκε στο Εδιμβούργο από διακεκριμένη σκοτσέζικη οικογένεια. Σπούδασε στο Κέιμπριτζ όπου διακρίθηκε. Δίδαξε σε διάφορα πανεπιστήμια στην Αγγλία καταλήγοντας στο Κέιμπριτζ. Είχε ιδιότυπη αίσθηση του χιούμορ, ήταν εξαιρετικά καλλιεργημένος, έγραφε ποίηση και ήταν μάλλον εσωστρεφής χαρακτήρας. Εικ. 5.11 James Clerk Maxwell (1831-1879). Ο κορυφαίος θεωρητικός φυσικός του 19ου αιώνα. Θεμελιωτής της σύγχρονης ηλεκτρομαγνητικής θεωρίας και ένας από τους θεμελιωτές της Θερμοδυναμικής και της Στατιστικής μηχανικής. Γεννήθηκε στο Εδιμβούργο από διακεκριμένη σκοτσέζικη οικογένεια. Σπούδασε στο Κέιμπριτζ όπου διακρίθηκε. Δίδαξε σε διάφορα πανεπιστήμια στην Αγγλία καταλήγοντας στο Κέιμπριτζ. Είχε ιδιότυπη αίσθηση του χιούμορ, ήταν εξαιρετικά καλλιεργημένος, έγραφε ποίηση και ήταν μάλλον εσωστρεφής χαρακτήρας.
|
ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL (ΜΑΞΓΟΥΕΛ) Στις αρχές του 19ου αιώνα οι ερευνητές είχαν αντιληφθεί ότι ο ηλεκτρισμός και ο μαγνητισμός είναι συγγενή φαινόμενα.
Το 1820 ο Oersted έδειξε με το περίφημο πείραμά του ότι ένα ηλεκτρικό ρεύμα δημιουργεί γύρω του μαγνητικό πεδίο.
Το 1831 ο Faraday και ο Henry, ανεξάρτητα ο ένας από τον άλλο, παρατήρησαν ότι όταν μεταβάλλεται η μαγνητική ροή μέσα από ένα κύκλωμα στο κύκλωμα επάγεται ηλεκτρεγερτική δύναμη.
Το 1865 ο James Clerk Maxwell λαμβάνοντας υπόψη όλη την προηγούμενη εμπειρία (Coulomb, Ampere, Faraday….) διατύπωσε τέσσερις εξισώσεις, που σήμερα είναι γνωστές ως εξισώσεις του Maxwell και περιγράφουν όλα τα ηλεκτρομαγνητικά φαινόμενα. Η σπουδαιότητα των εξισώσεων αυτών στον ηλεκτρομαγνητισμό είναι αντίστοιχη με τη σπουδαιότητα των νόμων του Newton στη μηχανική.
Ο Maxwell δε διατύπωσε όλες αυτές τις εξισώσεις μόνος του, τις έδωσε όμως σαν ένα ενιαίο σύνολο, επισήμανε τη σπουδαιότητά τους και μέσω αυτών προέβλεψε την ύπαρξη των ηλεκτρομαγνητικών κυμάτων, που διαδίδονται με την ταχύτητα του φωτός.
Τρεις από τις εξισώσεις αυτές τις γνωρίζετε ήδη
Η πρώτη είναι ο νόμος του Gauss
που συνδέει το ηλεκτρικό πεδίο με το ηλεκτρικό φορτίο που το δημιουργεί.
Η δεύτερη είναι ο νόμος του Gauss για το μαγνητισμό
που δηλώνει ότι δεν υπάρχουν μαγνητικά μονόπολα, δηλαδή δεν υπάρχει μαγνητικό αντίστοιχο του ηλεκτρικού φορτίου.
Η τρίτη είναι ο νόμος της επαγωγής του Faraday
Μια διάσταση αυτού του νόμου, την οποία δεν την αναλύσαμε, είναι ότι ένα μεταβαλλόμενο μαγνητικό πεδίο δημιουργεί ηλεκτρικό πεδίο.
Τέλος η τέταρτη εξίσωση είναι ο νόμος του Ampère, τροποποιημένος από το Maxwell. O νόμος του Ampere συνδέει το μαγνητικό πεδίο με τις πηγές του, που είναι τα ηλεκτρικά ρεύματα. Ο Maxwell τον τροποποίησε ως εξής |
Στη σχέση αυτή, ΦΕ είναι η ηλεκτρική ροή που διέρχεται από την κλειστή διαδρομή γύρω από την οποία υπολογίζεται το άθροισμα Bdl συνθ. Η ηλεκτρομαγνητική θεωρία, όπως τη διατύπωσε ο Maxwell, συνδέει το ηλεκτρικό και το μαγνητικό πεδίο με τις πηγές τους. Πηγές του ηλεκτρικού πεδίου δεν είναι μόνο τα φορτία αλλά και τα μεταβαλλόμενα μαγνητικά πεδία και πηγές του μαγνητικού πεδίου είναι όχι μόνο τα ρεύματα αλλά και τα μεταβαλλόμενα ηλεκτρικά πεδία. Σύμφωνα με τη θεωρία αυτή, η μεταβολή του ενός πεδίου συνεπάγεται και τη δημιουργία του άλλου. Κατά τον Maxwell τέτοιες μεταβολές ηλεκτρικού και μαγνητικού πεδίου πρέπει να διαδίδονται στο χώρο, όπως διαδίδονται τα ηχητικά ή τα υδάτινα κύματα. Στο κενό, οι διαταραχές αυτές πρέπει να διαδίδονται με την ταχύτητα c του φωτός. Λίγα χρόνια αργότερα ο Hertz (Χερτζ) επιβεβαίωσε πειραματικά τις προβλέψεις του Maxwell , παράγοντας ηλεκτρομαγνητικά κύματα στο εργαστήριο, και μετρώντας την ταχύτητά τους. Η ηλεκτρομαγνητική θεωρία, όπως διατυπώθηκε από το Maxwell, έπαιξε σπουδαίο, αν όχι το σπουδαιότερο, ρόλο στη διατύπωση της θεωρίας της σχετικότητας από τον Einstein. Με τη θεωρία της σχετικότητας πολλές βασικές έννοιες της φυσικής αναθεωρήθηκαν, οι εξισώσεις του Maxwell όμως παρέμειναν άθικτες. ΤΑ ΗΛΕΚΤΡΙΚΑ ΤΟΥ ΑΥΤΟΚΙΝΗΤΟΥ Ο ηλεκτρικός εξοπλισμός του αυτοκινήτου περιλαμβάνει: ΟΙ ΠΗΓΕΣ Η μπαταρία είναι συνήθως μολύβδου, έχει ΗΕΔ 12 V και μπορεί να παρέχει μέγιστο ρεύμα από 150 Α έως 250 Α. Το δυναμό είναι μια ηλεκτρογεννήτρια που εκμεταλλεύεται την κίνηση του κινητήρα του αυτοκινήτου για να παράγει ηλεκτρική ενέργεια. Η μπαταρία φορτίζεται από το δυναμό όταν ο κινητήρας είναι σε λειτουργία. Το δυναμό συνοδεύεται από ένα ρυθμιστή (αυτόματος) που κάνει δυο δουλειές. |
 Εικ. 5.12 Ηeinrich Rudolph Hertz (1857-1894). Γόνος ευκατάστατης μεγαλοαστικής οικογένειας του Αμβούργου. Γνώριζε πολλές ξένες γλώσσες μεταξύ των οποίων και αραβικά. Διάβαζε τον Όμηρο στο πρωτότυπο. Μαθητής και βοηθός του Helmholtz διακρίθηκε για την φοβερή πειραματική του επιδεξιότητα. Προσπάθησε ίσως περισσότερο από οποιονδήποτε άλλο να επιβεβαιώσει πειραματικά την ηλεκτρομαγνητική θεωρία του Maxwell και τα κατάφερε. Πέθανε σε ηλικία τριανταέξι ετών, θύμα της "ζήλιας των θεών", όπως είπε ο Helmholtz όταν έμαθε για το θάνατό του.

|
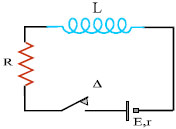
 Σχ. 5.64 Σχ. 5.64
 Σχ. 5.64 Σχ. 5.64
|
ΟΙ ΚΑΤΑΝΑΛΩΤΕΣ ΕΝΕΡΓΕΙΑΣ
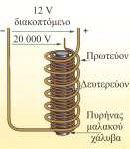
Τα μπουζί Για να παραχθεί σπινθήρας ανάμεσα στα ηλεκτρόδια ενός μπουζί, που απέχουν μεταξύ τους από 0,5 mm έως 0,7 mm, μέσα σ’ ένα συμπιεσμένο μίγμα αέρος – βενζίνης, πρέπει να εφαρμόσουμε μια τάση γύρω στα 10.000 V. Την τάση αυτή την πετυχαίνουμε με τη βοήθεια δύο σωληνοειδών τυλιγμένων γύρω από ένα πυρήνα μαλακού χάλυβα. Το ένα σωληνοειδές (πρωτεύον) έχει λίγες σπείρες και τροφοδοτείται με χαμηλή τάση. Το δεύτερο σωληνοειδές (δευτερεύον) έχει περίπου 20.000 σπείρες. Ένα είδος διακόπτη (οι πλατίνες) μεταβάλλει το ρεύμα στο πρωτεύον διακόπτοντάς το και αποκαθιστώντας το διαδοχικά. Χάρη στο φαινόμενο της αμοιβαίας επαγωγής στα άκρα του δευτερεύοντος αναπτύσσονται τάσεις από 10.000 V έως 30.000 V. Αυτή η υψηλή τάση κατανέμεται στα μπουζί με τη σειρά με την οποία πρέπει να λειτουργήσουν.
Η μίζα Η μίζα είναι ένας μικρός ηλεκτροκινητήρας που καταναλώνει μεγάλα ποσά ηλεκτρικής ενέργειας. Γι’ αυτό συνδέεται απ’ ευθείας με τη μπαταρία με δυο καλώδια μεγάλης διατομής. Η μίζα έχει ανάγκη από ρεύμα 100 Α – 300 Α για να λειτουργήσει. Πρόκειται για ρεύμα 20 φορές μεγαλύτερο από αυτό που χρειάζονται τα φώτα του αυτοκινήτου. Εάν μετά από έξι ως επτά δευτερόλεπτα συνεχούς χρήσης της μίζας το αυτοκίνητο δεν πάρει μπροστά πρέπει να περιμένουμε ένα χρονικό διάστημα πριν ξαναδοκιμάσουμε. Η παραγωγή του ρεύματος αντιστοιχεί σε μια χημική αντίδραση στη μπαταρία που είναι προτιμότερο να συμβαίνει όσο πιο αργά γίνεται. Περιορίζοντας το χρόνο λειτουργίας της μίζας φθείρουμε λιγότερο τη μπαταρία.
Οι άλλοι καταναλωτές Αν και οι υπόλοιποι καταναλωτές δεν καταναλώνουν τα ποσά ηλεκτρικής ενέργειας που καταναλώνει η μίζα, καλό είναι να μην λειτουργούν όταν ο κινητήρας δε λειτουργεί γιατί εξαντλούν τη μπαταρία. Στον πίνακα που ακολουθεί αναφέρονται κάποιες τιμές κατανάλωσης ηλεκτρικής ισχύος
|