| ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ | 4 |
 |
|
 Εικ. 4.1 Hans Christian Oersted (1777-1851). Καθηγητής φυσικής στην Κοπεγχάγη, ανακάλυψε τη μαγνητική δράση των ηλεκτρικών ρευμάτων, ανοίγοντας τους ορίζοντες για τη μελέτη του ηλεκτρομαγνητισμού. Εικ. 4.1 Hans Christian Oersted (1777-1851). Καθηγητής φυσικής στην Κοπεγχάγη, ανακάλυψε τη μαγνητική δράση των ηλεκτρικών ρευμάτων, ανοίγοντας τους ορίζοντες για τη μελέτη του ηλεκτρομαγνητισμού.
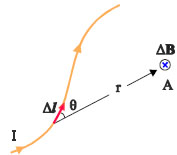 Σχ. 3.2 Το μαγνητικό πεδίο ΔB που δημιουργεί το τμήμα Δl του αγωγού στο σημείο Α, είναι κάθετο στο επίπεδο του βιβλίου και με φορά από τον αναγνώστη προς το βιβλίο. Η φορά δηλώνεται με το ⊗. Σχ. 3.2 Το μαγνητικό πεδίο ΔB που δημιουργεί το τμήμα Δl του αγωγού στο σημείο Α, είναι κάθετο στο επίπεδο του βιβλίου και με φορά από τον αναγνώστη προς το βιβλίο. Η φορά δηλώνεται με το ⊗. |
4-1 ΕΙΣΑΓΩΓΗ
Τα μεγάλα βήματα στην επιστήμη γίνονται στα ερευνητικά κέντρα που συγκεντρώνουν τους κορυφαίους επιστήμονες του καιρού τους και είναι εφοδιασμένα με τα πιο εξελιγμένα όργανα. Ο κανόνας, βέβαια, είχε τις εξαιρέσεις του. Στις εξαιρέσεις του κανόνα, ένας Δανός δάσκαλος της φυσικής σε σχολείο της Κοπεγχάγης, ο Hans Christian Oersted (Έρστεντ), κατά τη διάρκεια ενός πειράματος που έκανε στην τάξη του, παρατήρησε κάτι που στον καιρό του ήταν απίστευτο: το ηλεκτρικό ρεύμα επηρεάζει τη μαγνητική πυξίδα. Μέχρι τότε γνώριζαν την ύπαρξη των μόνιμων μαγνητών και τη μεταξύ τους αλληλεπίδραση. Το πείραμα του Oersted έδειξε ότι και το ηλεκτρικό ρεύμα επιδρά στους μαγνήτες. Λίγο αργότερα, ο Γάλλος φυσικός Ampère, κάνοντας ένα βήμα μπροστά, υποστήριξε ότι το ηλεκτρικό ρεύμα είναι η μοναδική πηγή των μαγνητικών φαινομένων. Την ερμηνεία της σχέσης ανάμεσα στην κίνηση φορτίου και το μαγνητισμό την έδωσε πολύ αργότερα, το 1905, η θεωρία της σχετικότητας. Οι αλληλεπιδράσεις μεταξύ μαγνητών ή μεταξύ μαγνητών και κινούμενων φορτίων είναι αλληλεπιδράσεις από απόσταση και γι’ αυτό η έννοια του πεδίου προσφέρεται για την περιγραφή τους. Αυτή τη φορά θα μιλήσουμε για το μαγνητικό πεδίο. Όπως κάναμε και στην περίπτωση των δυο άλλων πεδίων που μελετήσαμε, το μαγνητικό πεδίο θα το περιγράφουμε με την έντασή του (τη λένε και μαγνητική επαγωγή του πεδίου). Για λόγους απλότητας, θα λέμε «το μαγνητικό πεδίο Β» και θα εννοούμε «το μαγνητικό πεδίο που έχει ένταση Β». Στο κεφάλαιο αυτό θα ασχοληθούμε αρχικά με τις πηγές του μαγνητικού πεδίου, που είναι τα ρεύματα, και στη συνέχεια με τις δυνάμεις που ασκούν τα μαγνητικά πεδία. Τα μαγνητικά πεδία που θα εξετάσουμε θα είναι σταθερά.
4-2 ΝΟΜΟΣ ΤΩΝ BIOT ΚΑΙ SAVART
Λίγο μετά την ανακάλυψη του Oersted ότι το ηλεκτρικό ρεύμα δημιουργεί γύρω του μαγνητικό πεδίο, οι Biot και Savart (Μπιό και Σαβάρ), βασιζόμενοι σε πειραματικές μετρήσεις, κατέληξαν στο νόμο που δίνει το μαγνητικό πεδίο που δημιουργεί ένας αγωγός ο οποίος διαρρέεται από ρεύμα.
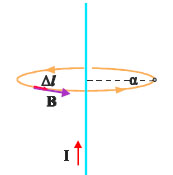
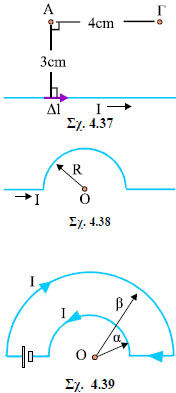
Αν ένας αγωγός διαρρέεται από ρεύμα έντασης Ι, ένα πολύ μικρό τμήμα του, μήκους Δl, δημιουργεί σε ένα σημείο Α που απέχει απόσταση r από το τμήμα Δl μαγνητικό πεδίο ΔB μέτρου
Στη σχέση αυτή το θ είναι η γωνία που σχηματίζουν τα διανύσματα Δl και r. H σταθερά μ0 λέγεται μαγνητική διαπερατότητα του κενού. Το διάνυσμα ΔB είναι κάθετο στο επίπεδο που ορίζεται από το Δl και το r και η φορά του δίνεται από τον κανόνα του δεξιού χεριού. |
Aν τοποθετήσουμε την παλάμη του δεξιού χεριού στο επίπεδο που ορίζεται από το Δl και το σημείο Α, έτσι ώστε ο αντίχειρας να δείχνει τη φορά του ρεύματος και τα υπόλοιπα δάχτυλα να βρίσκονται από την πλευρά του σημείου Α, τότε, αν τα κάμψουμε, τα υπόλοιπα δάχτυλα θα δείξουν τη φορά του ΔΒ.
Το μαγνητικό πεδίο Β, στο SI, μετριέται σε Tesla (T). Η μαγνητική διαπερατότητα του κενού είναι μο= 4x10-7 Tm / A
Ο νόμος των Biot και Savart, δίνει το μαγνητικό πεδίο που δημιουργείται από ένα μόνο πολύ μικρό τμήμα του αγωγού. Για να βρούμε το μαγνητικό πεδίο που δημιουργεί σε ένα σημείο ολόκληρος ο αγωγός, πρέπει να χωρίσουμε τον αγωγό σε πολύ μικρά τμήματα και στη συνέχεια να αθροίσουμε (διανυσματικά) τα πεδία που δημιουργούν όλα τα μικρά τμήματα του αγωγού στο σημείο που εξετάζουμε.
Από το σχήμα 3.4 βλέπουμε ότι A' = A' συνθ. Εφόσον ο αριθμός των δυναμικών γραμμών που διέρχονται από την Α είναι ίσος με τον αριθμό των γραμμών που διέρχονται από την Α΄, η ηλεκτρική ροή που διέρχεται από την επιφάνεια Α είναι ίση με τη ροή που διέρχεται από την επιφάνεια Α΄. Επειδή A' = A' συνθ και η ροή που διέρχεται από την επιφάνεια Α είναι
Ο νόμος των Biot και Savart είναι θεμελιώδης νόμος στο μαγνητισμό και παίζει ρόλο ανάλογο με εκείνο του νόμου του Coulomb στο στατικό ηλεκτρισμό.
4-3 ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΝΟΜΟΥ ΤΩΝ ΒΙΟΤ ΚΑΙ
SAVART
To μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού
Έστω το ευθύγραμμο σύρμα του σχήματος 4.2, μήκους L που διαρρέεται από ρεύμα έντασης Ι. Για να υπολογίσουμε το μαγνητικό πεδίο που δημιουργεί ο αγωγός στο σημείο Α, που απέχει απόσταση α από τον αγωγό, χωρίζουμε τον αγωγό σε πολύ μικρά τμήματα. Έστω ένα τέτοιο τμήμα μήκους Δl που απέχει απόσταση r από το σημείο Α. Το μικρό αυτό τμήμα δημιουργεί στο σημείο Α μαγνητικό πεδίο μέτρου
Το ΔB είναι κάθετo στο επίπεδο της σελίδας με φορά προς τον αναγνώστη.
Για να βρούμε το πεδίο που δημιουργεί ολόκληρος ο αγωγός, στο σημείο Α, αθροίζουμε τα πεδία όλων των τμημάτων στα οποία έχουμε χωρίσει τον αγωγό. Ο υπολογισμός του αθροίσματος αυτού απαιτεί τη χρήση ολοκληρωμάτων και υπερβαίνει το επίπεδο των μαθηματικών αυτού του βιβλίου. Το άθροισμα δίνει:
Αν το σύρμα έχει άπειρο μήκος (μήκος πολύ μεγαλύτερο από την απόσταση α) οι γωνίες θ1 και θ2 παίρνουν τιμές 0 και π αντίστοιχα, και η (4.2) δίνει:
|
 Eικ. 4.2 Jean Baptiste Biot (1774-1862). Γαλλία. Απόφοιτος της περίφημης École Polythechnique και καθηγητής στο Colège de France. Ασχολήθηκε σχεδόν με όλους τους τομείς της Φυσικής. Συνεργάστηκε με τον Savart σε μια θεωρία για το μαγνητισμό. Βραβεύθηκε από τη βασιλική εταιρεία επιστημών της Αγγλίας, κάτι ασυνήθιστο αν λάβει κανείς υπόψη του την εχθρότητα που υπήρχε στην εποχή του ανάμεσα στην Αγγλία και τη Γαλλία και στο επιστημονικό πεδίο. Eικ. 4.2 Jean Baptiste Biot (1774-1862). Γαλλία. Απόφοιτος της περίφημης École Polythechnique και καθηγητής στο Colège de France. Ασχολήθηκε σχεδόν με όλους τους τομείς της Φυσικής. Συνεργάστηκε με τον Savart σε μια θεωρία για το μαγνητισμό. Βραβεύθηκε από τη βασιλική εταιρεία επιστημών της Αγγλίας, κάτι ασυνήθιστο αν λάβει κανείς υπόψη του την εχθρότητα που υπήρχε στην εποχή του ανάμεσα στην Αγγλία και τη Γαλλία και στο επιστημονικό πεδίο.
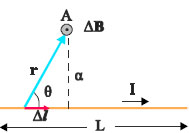 Σχ. 4.2 Στο σημείο Α το μαγνητικό πεδίο οφείλεται στη συνεισφορά όλων των πολύ μικρών τμημάτων Δl του ευθύγραμμου ρευματοφόρου αγωγού. Σχ. 4.2 Στο σημείο Α το μαγνητικό πεδίο οφείλεται στη συνεισφορά όλων των πολύ μικρών τμημάτων Δl του ευθύγραμμου ρευματοφόρου αγωγού.
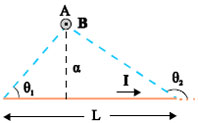 Σχ. 4.3 Στο σχήμα φαίνονται οι γωνίες θ1 και θ2 της σχέσης (4.2).. Σχ. 4.3 Στο σχήμα φαίνονται οι γωνίες θ1 και θ2 της σχέσης (4.2)..
|
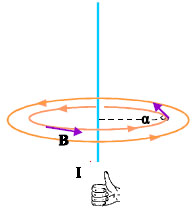 Σχ. 3.5 Με τον κανόνα του δεξιού χεριού μπορούμε να βρούμε τη φορά των δυναμικών γραμμών του πεδίου που δημιουργεί ο αγωγός. Σχ. 3.5 Με τον κανόνα του δεξιού χεριού μπορούμε να βρούμε τη φορά των δυναμικών γραμμών του πεδίου που δημιουργεί ο αγωγός.
Σχ. 3.6 Αισθητοποίηση του μαγνητικού πεδίου ευθύγραμμου αγωγού με ρινίσματα σιδήρου.
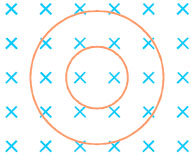
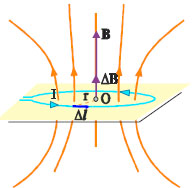 Σχ. 3.7 Το μαγνητικό πεδίο που δημιουργεί κυκλικός ρευματοφό-ρος αγωγός στο κέντρο του είναι κάθετο στο επίπεδο του κύκλου με φορά που βρίσκεται με τον κανόνα του δεξιού χεριού. Σχ. 3.7 Το μαγνητικό πεδίο που δημιουργεί κυκλικός ρευματοφό-ρος αγωγός στο κέντρο του είναι κάθετο στο επίπεδο του κύκλου με φορά που βρίσκεται με τον κανόνα του δεξιού χεριού.
|
Το μέτρο του Β είναι σταθερό σε κάθε σημείο κύκλου ακτίνας α και η διεύθυνσή του, σε κάθε σημείο, κάθετη στο επίπεδο που ορίζεται από τον αγωγό και το σημείο. Οι δυναμικές γραμμές ενός τέτοιου πεδίου είναι ομόκεντροι κύκλοι με κέντρο πάνω στον αγωγό και με το επίπεδό τους κάθετο σ΄ αυτόν. Το σχήμα 4.4 δίνει την τρισδιάστατη απεικόνιση του πεδίου που δημιουργεί ένας ευθύγραμμος ρευματοφόρος αγωγός πολύ μεγάλου μήκους. Η φορά των δυναμικών γραμμών μπορεί να βρεθεί εύκολα με τον κανόνα του δεξιού χεριού. Σύμφωνα με αυτόν, τοποθετούμε τον αντίχειρα του δεξιού χεριού στην κατεύθυνση του ρεύματος που διαρρέει τον αγωγό και κάμπτουμε τα υπόλοιπα δάχτυλα. Η φορά των δυναμικών γραμμών είναι ίδια με τη φορά που καθορίζουν τα δάχτυλα.

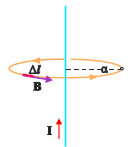
Το μαγνητικό πεδίο στο κέντρο κυκλικού ρευματοφόρου αγωγού.
Το σχήμα 4.5 δείχνει ένα κυκλικό αγωγό ακτίνας r που διαρρέεται από ρεύμα έντασης Ι. Για να υπολογίσουμε το μαγνητικό πεδίο που δημιουργεί ένας τέτοιος αγωγός στο κέντρο του, χωρίζουμε τον αγωγό σε πολύ μικρά τμήματα. Ένα τέτοιο τμήμα Δl1, σύμφωνα με το νόμο των Biot και Savart, δημιουργεί στο κέντρο Ο μαγνητικό πεδίο μέτρου
Η διεύθυνση του ΔΒ1 είναι κάθετη στο επίπεδο του κύκλου και η φορά του προς τα πάνω. Το επόμενο πολύ μικρό τμήμα, μήκους Δl2 δημιουργεί στο σημείο Ο μαγνητικό πεδίο μέτρου
ίδιας κατεύθυνσης με το ΔΒ1
Το μαγνητικό πεδίο Β που δημιουργεί ολόκληρος ο κυκλικός αγωγός προκύπτει από το διανυσματικό άθροισμα των πεδίων που δημιουργούν τα τμήματα του αγωγού, και επειδή όλα έχουν την ίδια κατεύθυνση,
|
Το άθροισμα Δl1 + Δl2+ ... δίνει την περίμετρο του κυκλικού αγωγού 2πr και η σχέση (4.4) γίνεται
Το Β, στο O, είναι κάθετο στο επίπεδο του κυκλικού αγωγού και η φορά του δίνεται από τον κανόνα του δεξιού χεριού.
4-4 Ο ΝΟΜΟΣ ΤΟΥ AMPERE (ΑΜΠΕΡ)
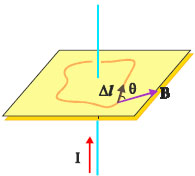
Ο νόμος του Ampère είναι μια γενική σχέση ανάμεσα στο μαγνητικό πεδίο και στις πηγές του. Είδαμε ότι ένας ευθύγραμμος ρευματοφόρος αγωγός δημιουργεί γύρω του μαγνητικό πεδίο της μορφής του σχήματος 4.6, με ένταση μέτρου
Ας χωρίσουμε μια δυναμική γραμμή σε πολύ μικρά τμήματα Δl και ας υπολογίσουμε το άθροισμα των γινομένων Β Δl συνθ κατά μήκος της δυναμικής γραμμής. θ είναι η γωνία ανάμεσα στο Δl και στο Β. Επειδή στο συγκεκριμένο πεδίο η γωνία αυτή είναι μηδέν, το συνημίτονο της γωνίας είναι μονάδα.
γράφεται
Αυτό σημαίνει ότι το άθροισμα του πρώτου μέλους είναι ανεξάρτητο της απόστασης α από τον αγωγό. Αποδεικνύεται ότι το αποτέλεσμα αυτό είναι γενικό και ισχύει για κάθε κλειστή διαδρομή μέσα από την οποία διέρχεται σταθερό ρεύμα. Στην περίπτωση που η κλειστή διαδρομή περικλείει περισσότερα του ενός ρεύματα - και δεν έχει σημασία αν οι αγωγοί είναι ευθύγραμμοι - κάθε ρεύμα που διέρχεται μέσα από το βρόχο (κλειστή διαδρομή) συνεισφέρει κατά μοΙ.
Στη συνέχεια θα δούμε ότι ο νόμος του Gauss δίνει εύκολα την ένταση του ηλεκτρικού πεδίου σε περιπτώσεις όπου έχουμε συμμετρική κατανομή φορτίου. |
Εικ. 4.4 Αισθητοποίηση του μαγνητικού πεδίου κυκλικού αγωγού με ρινίσματα σιδήρου.
 Εικ. 4.5 Andre Marie Ampère (1775-1836). Γαλλία. Καθηγητής της École Polythechnique. Διατύπωσε μια συνθετική θεωρία για τον ηλεκτρομαγνητισμό και απέδωσε τις μαγνητικές ιδιότητες κά-ποιων υλικών σε μικροσκοπικά κλειστά ρεύματα στο εσωτερικό της ύλης. Εικ. 4.5 Andre Marie Ampère (1775-1836). Γαλλία. Καθηγητής της École Polythechnique. Διατύπωσε μια συνθετική θεωρία για τον ηλεκτρομαγνητισμό και απέδωσε τις μαγνητικές ιδιότητες κά-ποιων υλικών σε μικροσκοπικά κλειστά ρεύματα στο εσωτερικό της ύλης.
 Σχ. 4.6 Κατά μήκος της δυναμι-κής γραμμής τα Δlκαι Β είναι συγγραμμικά (θ=0) Σχ. 4.6 Κατά μήκος της δυναμι-κής γραμμής τα Δlκαι Β είναι συγγραμμικά (θ=0) |
 Σχ. 4.7 To άθροισμα των γινομένων ΒΔl συνθ κατά μήκος οποιασδήποτε κλειστής διαδρομής που περικλείει το ρεύμα Ι είναι ίσο με μο I Σχ. 4.7 To άθροισμα των γινομένων ΒΔl συνθ κατά μήκος οποιασδήποτε κλειστής διαδρομής που περικλείει το ρεύμα Ι είναι ίσο με μο I
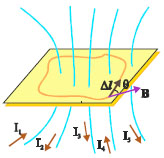
Σχ. 4.8 To άθροισμα των γινομέ-νων ΒΔlσυνθ κατά μήκος κλειστής διαδρομής είναι ίσο με τη σταθερά μο επί το αλγεβρικό άθροισμα των ρευμάτων που περικλείει η κλει-στή διαδρομή. Εδώ το αλγεβρικό άθροισμα των ρευμάτων είναι Ι1-Ι2-Ι3+Ι4.
|
Κατά μήκος μιας κλειστής διαδρομής το άθροισμα των γινομένων Β Δl συνθ ισούται με μοΙεγκ, όπου Ιεγκ, το αλγεβρικό άθροισμα των ρευμάτων που διέρχονται από την επιφάνεια η οποία περιβάλλεται από την κλειστή αυτή διαδρομή. (Nόμος Ampère).
Η φορά που αντιστοιχεί σε θετικό ρεύμα ορίζεται από τον κανόνα του δεξιού χεριού. Αν τα δάκτυλα του δεξιού χεριού, δείχνουν τη φορά κίνησης στο βρόχο, ο αντίχειρας ορίζει τη θετική φορά για τα ρεύματα.
Το Β στην παραπάνω σχέση οφείλεται τόσο στα ρεύματα που περικλείει ο βρόχος (κλειστή διαδρομή) όσο και σε ρεύματα που βρίσκονται έξω από αυτόν.
Πρέπει να τονιστεί ότι ο νόμος του Ampère ισχύει μόνο για σταθερά ρεύματα και για σταθερά μαγνητικά πεδία. Όπως ο νόμος του Gauss μάς επιτρέπει να υπολογίζουμε το ηλεκτρικό πεδίο που δημιουργείται από συμμετρικές κατανομές φορτίου, έτσι και ο νόμος του Ampère μάς διευκολύνει να υπολογίζουμε την ένταση σε μαγνητικά πεδία που εμφανίζουν συμμετρία.
|
ΠΑΡΑΔΕΙΓΜΑ 4.1 |
Υπολογισμός του μαγνητικού πεδίου που δημιουργεί ευθύγραμμος αγωγός με άπειρο μήκος, που διαρρέεται από ρεύμα σταθερής έντασης. (Tο ίδιο πρόβλημα το έχουμε αντιμετωπίσει χρησιμοποιώντας το νόμο των Biot και Savart).
Απάντηση:
Η συμμετρία της διάταξης επιβάλλει το μέτρο του μαγνητικού πεδίου που δημιουργεί ένας τέτοιος αγωγός να είναι ίδιο σε όλα τα σημεία που ισαπέχουν από τον αγωγό. Η διεύθυνση του πεδίου, σε κάθε σημείο, είναι κάθετη στο επίπεδο που σχηματίζει ο αγωγός και η απόσταση α του σημείου από αυτόν.
Για να εφαρμόσουμε το νόμο του Ampère επιλέγουμε μια κλειστή κυκλική διαδρομή ακτίνας α, με κέντρο πάνω στον αγωγό και το επίπεδό της κάθετο σ΄ αυτόν. Χωρίζουμε τη διαδρομή σε πολύ μικρά τμήματα Δl.
|
Θα υπολογίσουμε το άθροισμα των γινομένων Β Δl συνθ κατά μήκος της κυκλικής διαδρομής. Η κατεύθυνση των τμημάτων Δl σε κάθε σημείο είναι ίδια με την κατεύθυνση του Β σε εκείνο το σημείο επομένως η γωνία θ που σχηματίζουν είναι μηδέν και το συνημίτονό της μονάδα.
Φτάσαμε δηλαδή από άλλο δρόμο στη σχέση (4.3). |
 Σχ. 4.9 Εφαρμόζουμε το νόμο του Ampere σε κυκλική διαδρομή που συμπίπτει με μια δυναμική γραμμή. Σχ. 4.9 Εφαρμόζουμε το νόμο του Ampere σε κυκλική διαδρομή που συμπίπτει με μια δυναμική γραμμή. |
ΠΑΡΑΔΕΙΓΜΑ 4.2 |
||||||||||||||||
Υπολογισμός του μαγνητικού πεδίου σωληνοειδούς, απείρου μήκους, που διαρρέεται από ρεύμα σταθερής έντασης Ι.
Το άθροισμα των γινομένων Β Δl συνθ κατά μήκος της διαδρομής ΑΓ είναι Bl. Κατά μήκος των διαδρομών ΓΔ και ΕΑ το ίδιο άθροισμα είναι μηδέν γιατί, όπου υπάρχει, το μαγνητικό πεδίο είναι κάθετο στη διαδρομή. Επομένως συνθ = συν90o = 0. Τέλος, κατά μήκος της ΔΕ είναι επίσης μηδέν γιατί στην περιοχή αυτή δεν υπάρχει μαγνητικό πεδίο (Β=0). Επομένως Σύμφωνα με το νόμο του Ampere το άθροισμα αυτό είναι ίσο με το γινόμενο της σταθεράς μο επί το συνολικό ρεύμα που διαπερνά το ορθογώνιο πλαίσιο. Αν I το ρεύμα που διαρρέει κάθε σπείρα και Ν ο αριθμός των σπειρών που περιέχονται στο ορθογώνιο πλαίσιο, τότε το ολικό ρεύμα που διέρχεται είναι NI.
αν όπου Ν/l θέσουμε , όπου το αντιπροσωπεύει τον αριθμό των σπειρών ανά μονάδα μήκους, η σχέση (4.5) γίνεται:
Παρόλο που η σχέση (4.6) βρέθηκε για σωληνοειδές απείρου μήκους, δίνει με μεγάλη ακρίβεια το μαγνητικό πεδίο στο εσωτερικό οποιουδήποτε σωληνοειδούς με μεγάλο μήκος. Στα άκρα του σωληνοειδούς η τιμή του Β είναι μικρότερη, περίπου η μισή. |
 Σχ. 4.10 Η επιφάνεια Α είναι τοποθετημένη σε ομογενές μαγνητικό πεδίο ώστε το κάθετο σ’ αυτή διάνυσμα Α να σχηματίζει γωνία θ με τις δυναμικές γραμμές. Σχ. 4.10 Η επιφάνεια Α είναι τοποθετημένη σε ομογενές μαγνητικό πεδίο ώστε το κάθετο σ’ αυτή διάνυσμα Α να σχηματίζει γωνία θ με τις δυναμικές γραμμές.
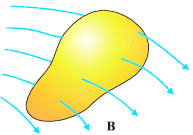 Σχ. 4.11 Για κάθε κλειστή επιφάνεια ο αριθμός των δυναμικών γραμμών που εισέρχονται είναι ίσος με τον αριθμό των γραμμών που εξέρχονται. Σχ. 4.11 Για κάθε κλειστή επιφάνεια ο αριθμός των δυναμικών γραμμών που εισέρχονται είναι ίσος με τον αριθμό των γραμμών που εξέρχονται.
|
4-5 ΜΑΓΝΗΤΙΚΗ ΡΟΗ
Η ροή του μαγνητικού πεδίου ορίζεται με τρόπο ανάλογο με αυτόν που ορίστηκε η ροή του ηλεκτρικού πεδίου. Έστω μια επίπεδη επιφάνεια εμβαδού Α μέσα σε ομογενές μαγνητικό πεδίο. Η μαγνητική ροή που διέρχεται από την επιφάνεια είναι
όπου θ η γωνία ανάμεσα στις δυναμικές γραμμές και σε μια κάθετη στην επιφάνεια Α. Μονάδα της μαγνητικής ροής είναι το 1Wb (Βέμπερ).
Αν η επιφάνεια Α δεν είναι επίπεδη ή αν το μαγνητικό πεδίο δεν είναι ομογενές ή αν συμβαίνουν και τα δύο, για να υπολογίσουμε τη μαγνητική ροή που διέρχεται από την επιφάνεια χωρίζουμε την επιφάνεια σε στοιχειώδη τμήματα ΔΑ, τόσο μικρά ώστε να μπορούν να θεωρηθούν επίπεδα και το μαγνητικό πεδίο στην περιοχή καθενός να μπορεί να θεωρηθεί σταθερό. Υπολογίζουμε τη ροή που διέρχεται από κάθε επιφάνεια ΔΑ. Το άθροισμα των μαγνητικών ροών που διέρχονται από αυτά τα στοιχειώδη τμήματα θα είναι η ροή που περνάει από την επιφάνεια Α.
4-6 Ο ΝΟΜΟΣ ΤΟΥ GAUSS ΣΤΟ ΜΑΓΝΗΤΙΣΜΟ
Στην παράγραφο 3-3 είδαμε ότι η ηλεκτρική ροή που διέρχεται από μια κλειστή επιφάνεια είναι ανάλογη με το φορτίο που περικλείει η επιφάνεια. Αντίθετα με ό,τι συμβαίνει στο ηλεκτρικό πεδίο, στο οποίο οι δυναμικές γραμμές είναι ανοικτές (ξεκινούν από φορτία ή καταλήγουν σε φορτία), στο μαγνητικό πεδίο οι γραμμές είναι κλειστές, δεν έχουν αρχή και τέλος. Συνέπεια αυτής τους της ιδιότητας είναι ότι για κάθε κλειστή επιφάνεια μέσα στο μαγνητικό πεδίο, ο αριθμός των δυναμικών γραμμών που εισέρχονται είναι πάντα ίσος με τον αριθμό των γραμμών που εξέρχονται. Άρα η μαγνητική ροή που διέρχεται από μια οποιαδήποτε κλειστή επιφάνεια είναι μηδέν.
Η μαγνητική ροή που διέρχεται από μια κλειστή επιφάνεια είναι πάντοτε
Το φυσικό περιεχόμενο αυτής της πρότασης είναι ότι δεν υπάρχουν σημειακές πηγές μαγνητικού πεδίου, όπως υπάρχουν στο ηλεκτρικό πεδίο Δηλαδή δεν υπάρχει μαγνητικό ανάλογο του φορτίου. Τόσο ο Coulomb, όσο και άλλοι πίστευαν ότι ο μαγνητισμός παράγεται από ΄΄κάτι΄΄ ανάλογο με το ηλεκτρικό φορτίο. Σήμερα αυτό το ανάλογο το αποκαλούμε μαγνητικό μονόπολο, που σημαίνει απομονωμένος μαγνητικός πόλος. Ο Αmpère ήταν ο πρώτος που υποστήριξε ότι όλα τα μαγνητικά φαινόμενα προέρχονται από ηλεκτρικά ρεύματα (φορτία σε κίνηση), και δικαιώθηκε. Σε κανένα πείραμα μέχρι τώρα δεν έχουν βρεθεί μαγνητικά μονόπολα. Η ύπαρξη ενός μονόπολου θα ήταν εύκολο να ανιχνευτεί γιατί θα δημιουργούσε ακτινικό μαγνητικό πεδίο. Η σχέση (4.7) δείχνει ότι δεν υπάρχουν άλλες πηγές μαγνητικού πεδίου εκτός από τα ρεύματα. |
4-7 ΔΥΝΑΜΗ ΠΟΥ ΑΣΚΕΙ ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ
ΣΕ ΚΙΝΟΥΜΕΝΟ ΦΟΡΤΙΟ
Ένα ακίνητο φορτισμένο σωματίδιο δεν αντιδρά μέσα σε ένα στατικό μαγνητικό πεδίο. Αν όμως κινείται εκτρέπεται από την πορεία του, ένδειξη ότι το σωματίδιο δέχεται δύναμη από το μαγνητικό πεδίο.
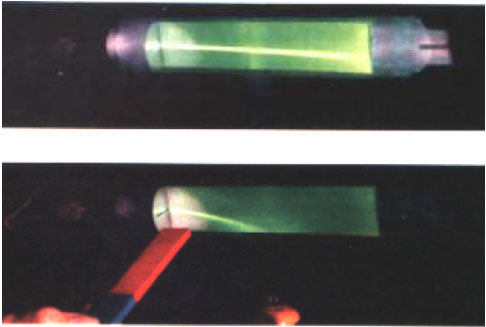
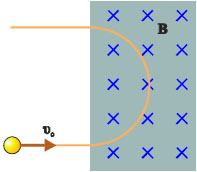
Υπάρχουν διάφορες τεχνικές που μας επιτρέπουν να παρακολουθήσουμε τη συμπεριφορά κινούμενων σωματιδίων μέσα στο μαγνητικό πεδίο Η εικόνα 4.6 δείχνει πώς μπορούμε να διαπιστώσουμε την εκτροπή που υφίσταται μια δέσμη ηλεκτρονίων από το μαγνητικό πεδίο.
Από την εκτροπή που υφίσταται ένα φορτισμένο σωματίδιο προκύπτει ότι η δύναμη που δέχεται από το μαγνητικό πεδίο είναι ανάλογη του μαγνητικού πεδίου, του φορτίου, της ταχύτητας του σωματίου και εξαρτάται και από την κατεύθυνση της κίνησης. Η δύναμη μεγιστοποιείται όταν το φορτισμένο σωματίδιο κινείται κάθετα στις δυναμικές γραμμές. Σε άλλες κατευθύνσεις ελαττώνεται και μηδενίζεται όταν κινείται παράλληλα στις δυναμικές γραμμές. Σε κάθε περίπτωση η δύναμη αυτή, όταν ασκείται, είναι κάθετη στη διεύθυνση του μαγνητικού πεδίου και στην ταχύτητα.
|
Εικ. 4.6 Σημειακό φορτίο Q δημιουργεί στο χώρο ηλεκτρικό πεδίο. Το δυναμικό στο σημείο Α του πεδίου είναι
Σχ. 4.13 (α) Όταν η δέσμη των ηλεκτρονίων στον καθοδικό σωλήνα είναι παράλληλη με το διάνυσμα Β δεν υφίσταται εκτροπή. (β) Όταν η δέσμη κινείται σε οποιαδήποτε άλλη διεύθυνση εκτρέπεται. Η μέγιστη εκτροπή παρατηρείται όταν η δέσμη είναι κάθετη στο Β |
 Εικ. 4.7 Ο κανόνας των τριών δακτύλων του δεξιού χεριού. Εικ. 4.7 Ο κανόνας των τριών δακτύλων του δεξιού χεριού. |
Η δύναμη που ασκεί το μαγνητικό πεδίο στα κινούμενα φορτία δεν έχει την ίδια διεύθυνση με την ένταση του πεδίου, όπως συμβαίνει με το ηλεκτρικό και το βαρυτικό πεδίο.
Η φορά της δύναμης εξαρτάται από το πρόσημο του φορτίου. Φορτία με αντίθετο πρόσημο δέχονται δυνάμεις αντίθετης κατεύθυνσης.
Πειράματα ακριβείας έδειξαν ότι:
Το μαγνητικό πεδίο ασκεί στα κινούμενα ηλεκτρικά φορτία δύναμη [ονομάζεται δύναμη Lorentz (Λόρεντζ)] μέτρου
όπου φ η γωνία που σχηματίζει η ταχύτητα του σωματιδίου με την κατεύθυνση του μαγνητικού πεδίου. Η δύναμη αυτή είναι κάθετη στο επίπεδο που ορίζεται από την ταχύτητα και τη διεύθυνση του πεδίου και η φορά της δίνεται από τον κανόνα των τριών δακτύλων του δεξιού χεριού.
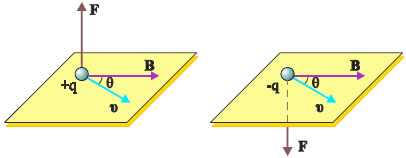
Ο κανόνας των τριών δακτύλων του δεξιού χεριού εφαρμόζεται ως εξής: Ο αντίχειρας, ο δείκτης και ο μέσος σχηματίζουν τρισορθογώνιο σύστημα. Τοποθετούμε τον αντίχειρα στην κατεύθυνση της κίνησης του θετικού φορτίου και στην αντίθετη αν πρόκειται για αρνητικό. Τοποθετούμε το δείκτη στην κατεύθυνση του μαγνητικού πεδίου (Β). Ο μέσος δείχνει τότε την κατεύθυνση της δύναμης (εικ.4.7).
Εφόσον η δύναμη είναι πάντα κάθετη στην ταχύτητα του φορτίου, είναι κάθετη σε κάθε στοιχειώδη μετατόπισή του. Επομένως το έργο της σε κάθε τέτοια στοιχειώδη μετατόπιση είναι μηδέν. Συνδυάζοντας το συμπέρασμα αυτό με το θεώρημα έργου - ενέργειας συμπεραίνουμε ότι η δύναμη αυτή δε μπορεί να μεταβάλει την κινητική ενέργεια του φορτισμένου σωματιδίου
Όταν ένα φορτισμένο σωματίδιο κινείται με ταχύτητα υ, μέσα σε μαγνητικό πεδίο, η δύναμη που του ασκεί το πεδίο μπορεί να μεταβάλει την κατεύθυνση αλλά όχι και το μέτρο της ταχύτητάς του.
|
4-8 ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙΔΙΩΝ ΜΕΣΑ
ΣΕ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ
Ένα φορτισμένο σωματίδιο που κινείται μέσα στο μαγνητικό πεδίο δέχεται από αυτό δύναμη που εξαρτάται από την ταχύτητά του. Θα μελετήσουμε ορισμένες ειδικές περιπτώσεις της κίνησης φορτισμένου σωματιδίου μέσα στο μαγνητικό πεδίο.
Α) Κίνηση παράλληλα στις δυναμικές γραμμές
Αν ένα φορτισμένο σωματίδιο κινείται παράλληλα στις δυναμικές γραμμές, η γωνία φ στη σχέση (4.8) είναι ή 0o ή 180o. Και στις δυο περιπτώσεις το ημίτονο της γωνίας είναι μηδέν, οπότε από τη σχέση (4.8) προκύπτει ότι το μαγνητικό πεδίο δεν ασκεί δύναμη στο σωματίδιο. Η κίνηση ενός τέτοιου σωματιδίου μέσα στο μαγνητικό πεδίο είναι ευθύγραμμη ομαλή.
B) Κίνηση κάθετα στις δυναμικές γραμμές
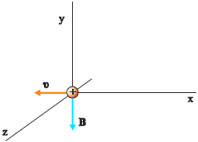
Έστω ένα φορτισμένο σωματίδιο που κινείται με ταχύτητα υ κάθετη στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου που έχει κατεύθυνση κάθετη στο επίπεδο της σελίδας με φορά προς τα μέσα1 (σχ.4.15). Το μαγνητικό πεδίο ασκεί στο σωματίδιο δύναμη το μέτρο της οποίας είναι
που προκύπτει από την (4.8), αν λάβουμε υπόψη ότι ημ90o=1
Η κατεύθυνση της δύναμης, για θετικά φορτισμένο σωματίδιο, φαίνεται στο σχήμα 4.15 Η δύναμη αυτή έχει σταθερό μέτρο και είναι πάντα κάθετη στην ταχύτητα. Μια τέτοια δύναμη παίζει ρόλο κεντρομόλου δύναμης και αναγκάζει το σωματίδιο να κινηθεί κυκλικά. Ένα φορτισμένο σωματίδιο που κινείται μέσα σε ομογενές μαγνητικό πεδίο, κάθετα στις δυναμικές γραμμές, κάνει ομαλή κυκλική κίνηση.
Εφόσον η δύναμη παίζει ρόλο κεντρομόλου δύναμης, θα ισχύει
όπου η ακτίνα της κυκλικής τροχιάς που διαγράφει το σωματίδιο. Από τις σχέσεις (4.9) και (4.10) έχουμε
1 Η κατεύθυνση αυτού του πεδίου συμβολίζεται με x. Είναι σαν να βλέπουμε το πίσω μέρος ενός βέλους που διαπερνά κάθετα τη σελίδα του βιβλίου, κατευθυνόμενο από τον αναγνώστη προς αυτήν. Αντίθετα θα συμβολίζουμε με απλές κουκίδες ένα μαγνητικό πεδίο που κατευθύνεται από τη σελίδα προς τον αναγνώστη, απεικονίζοντας έτσι την αιχμή ενός βέλους. |
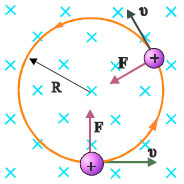 Σχ. 4.15 Θετικά φορτισμένο σωματίδιο που κινείται με ταχύτητα υ, κάθετα στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου, δέχεται δύναμη σταθερού μέτρου, κάθετη στην ταχύτητά του. Το σωματίδιο διαγράφει κυκλική τροχιά μέσα στο μαγνητικό πεδίο. Σχ. 4.15 Θετικά φορτισμένο σωματίδιο που κινείται με ταχύτητα υ, κάθετα στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου, δέχεται δύναμη σταθερού μέτρου, κάθετη στην ταχύτητά του. Το σωματίδιο διαγράφει κυκλική τροχιά μέσα στο μαγνητικό πεδίο.
 Εικ. 4.8 Πειραματική διάταξη για τη μελέτη της εκτροπής μιας δέσμης ηλεκτρονίων μέσα σε μαγνητικό πεδίο. Το μαγνητικό πεδίο είναι κάθετο στη διεύθυνση κίνησης της δέσμης. Τα ηλεκτρόνια κινούνται κυκλικά. Εικ. 4.8 Πειραματική διάταξη για τη μελέτη της εκτροπής μιας δέσμης ηλεκτρονίων μέσα σε μαγνητικό πεδίο. Το μαγνητικό πεδίο είναι κάθετο στη διεύθυνση κίνησης της δέσμης. Τα ηλεκτρόνια κινούνται κυκλικά. |
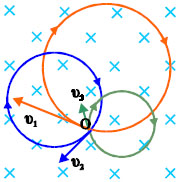 Σχ. 4.16 Τρία ηλεκτρόνια βάλλονται με διαφορετικές ταχύτητες κάθετα στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου στο σημείο Ο. Η ακτίνα της κυκλικής τροχιάς είναι ανάλογη της ταχύτητας. Η περίοδος είναι ίδια και στις τρεις περιπτώσεις. Σχ. 4.16 Τρία ηλεκτρόνια βάλλονται με διαφορετικές ταχύτητες κάθετα στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου στο σημείο Ο. Η ακτίνα της κυκλικής τροχιάς είναι ανάλογη της ταχύτητας. Η περίοδος είναι ίδια και στις τρεις περιπτώσεις. 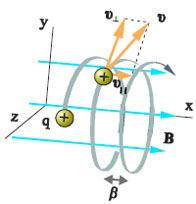 Σχ. 4.17 Κίνηση φορτισμένου σωματιδίου που βάλλεται πλάγια στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου. Σχ. 4.17 Κίνηση φορτισμένου σωματιδίου που βάλλεται πλάγια στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου.
|
Η περίοδος περιστροφής του σωματιδίου βρίσκεται αν πάρουμε υπόψη ότι
Η τελευταία σχέση δείχνει ότι η περίοδος περιστροφής, δεν εξαρτάται από την ταχύτητα ή την ακτίνα της κυκλικής τροχιάς αλλά μόνο από το είδος του σωματιδίου (μάζα και φορτίο). Έτσι, αν σε ένα μαγνητικό πεδίο κινούνται κάθετα στις δυναμικές γραμμές του ηλεκτρόνια που έχουν διαφορετικές ταχύτητες, θα διαγράφουν κύκλους διαφορετικών ακτίνων αλλά οι περίοδοι περιστροφής τους θα είναι ίδιες (σχ.4.16).
Γ) Κίνηση με τυχαία γωνία ως προς τις δυναμικές γραμμές
Έστω ένα σωματίδιο που εισέρχεται σε ομογενές μαγνητικό πεδίο και η κατεύθυνση της ταχύτητας σχηματίζει με τις δυναμικές γραμμές γωνία 0<φ<90o. Αναλύουμε την ταχύτητά του υ σε μια συνιστώσα παράλληλη (υ|) και μια κάθετη (υ⊥) στις δυναμικές γραμμές. Αν το σωματίδιο είχε μόνο τη υ| θα έκανε ευθύγραμμη ομαλή κίνηση (περίπτωση Α). Αν είχε μόνο τη υ⊥θα έκανε ομαλή κυκλική κίνηση (περίπτωση Β). Από τη σύνθεση των δύο κινήσεων προκύπτει μια ελικοειδής κίνηση
Σε χρόνο μιας περιόδου το σωματίδιο προχωράει στη διεύθυνση του άξονα
σώμα στη διεύθυνση του πεδίου στο χρόνο κάθε περιόδου ονομάζεται βήμα της έλικας.
Δ) Κίνηση σε ανομοιογενές μαγνητικό πεδίο
Η τροχιά που διαγράφει ένα φορτισμένο σωματίδιο μέσα σε ανομοιογενές μαγνητικό πεδίο είναι γενικά πολύπλοκη και εξαρτάται κάθε φορά από τη μορφή του πεδίου.
Το σχήμα 4.18 δείχνει ένα ανομοιογενές πεδίο που δημιουργείται από δυο κυκλικά πηνία (πηνία που το μήκος τους είναι πολύ μικρότερο από τη διάμετρό τους), τα οποία έχουν τοποθετηθεί σε μεγάλη απόσταση, με τα επίπεδά τους παράλληλα. Ένα τέτοιο πεδίο είναι ισχυρό κοντά στα πηνία και ασθενές στο μέσο της διάταξης.
Ένα φορτισμένο σωματίδιο που ξεκινάει από το ένα άκρο του πεδίου κάνει ελικοειδή κίνηση. Όταν φτάσει στο άλλο άκρο του πεδίου η κίνησή του αναστρέφεται και το σωματίδιο, διαγράφοντας και πάλι ελικοειδή τροχιά, |
επιστρέφει στο σημείο εκκίνησης. Η κίνηση αυτή του σωματιδίου επαναλαμβάνεται διαρκώς
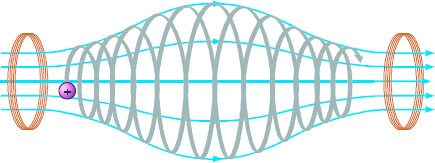
Ένα τέτοιο πεδίο παγιδεύει τα φορτισμένα σωματίδια και αναφέρεται συχνά ως «μαγνητική φιάλη».
Σε μαγνητικές φιάλες έχει επιτευχθεί η παγίδευση μεγάλων ποσοτήτων πλάσματος (δηλαδή «αερίου» που βρίσκεται σε θερμοκρασία πάνω από 106 Κ και αποτελείται από ηλεκτρόνια και θετικά ιόντα). Η παγίδευση του πλάσματος είναι ένα από τα προβλήματα που πρέπει να λυθούν προκειμένου να επιτύχουμε ελεγχόμενη θερμοπυρηνική σύντηξη και να εκμεταλλευτούμε για ειρηνικούς σκοπούς την ενέργεια που μας δίνει.
Μια μαγνητική φιάλη, που μόλις περιγράψαμε, σχηματίζει το μαγνητικό πεδίο της Γης. Όπως είναι γνωστό, οι δυναμικές γραμμές του μαγνητικού πεδίου της Γης έχουν ίδια μορφή με τις δυναμικές γραμμές του μαγνητικού πεδίου ενός ευθύγραμμου μαγνήτη που θα είχε τους πόλους του κοντά στους γεωγραφικούς πόλους της Γης. Οι δυναμικές γραμμές αυτού του πεδίου είναι πυκνότερες στους πόλους.
Στην ατμόσφαιρα της Γης εισέρχονται φορτισμένα σωματίδια, κυρίως ηλεκτρόνια και πρωτόνια, που στο μεγάλο μέρος τους προέρχονται από τον Ήλιο. Μερικά από τα σωματίδια αυτά εγκλωβίζονται στο μαγνητικό πεδίο της Γης και κινούνται διαρκώς από τον ένα πόλο στον άλλο.
Το 1958, διαπιστώθηκε από τις καταγραφές των οργάνων που έφερε ο δορυφόρος Explorer 1 ότι η Γη περιβάλλεται από δυο ζώνες στις οποίες παρατηρήθηκε μεγάλη πυκνότητα φορτισμένων σωματιδίων. Οι ζώνες αυτές ονομάστηκαν ζώνες Van Allen (Βαν Άλεν) και αποτελούνται από δυο δακτυλίους που απέχουν από τη Γη 3.000 km, ο εσωτερικός, και 15.000 km, ο εξωτερικός.
Η πυκνότητα των φορτισμένων σωματιδίων είναι ιδιαίτερα μεγάλη κοντά στους πόλους, όπου οι δυναμικές γραμμές του πεδίου πυκνώνουν. Εκεί, οι κρούσεις των φορτισμένων σωματιδίων με τα άτομα των αερίων της ατμόσφαιρας έχουν ως αποτέλεσμα την εκπομπή ορατής ακτινοβολίας. Η ακτινοβολία αυτή ονομάζεται «ακτινοβολία Cerenkov» (Τσερένκοφ).
Το βόρειο σέλας,που απεικονίζεται στο εξώφυλλο αυτού του βιβλίου και στην εικόνα 4.9, είναι αποτέλεσμα αυτής της ακτινοβολίας. Αντίστοιχο φαινόμενο, βέβαια, εκδηλώνεται και κοντά στο νότιο πόλο. |
Σχ. 4.18 Μαγνητική φιάλη.
 Εικ. 4.9 Βόρειο σέλας Εικ. 4.9 Βόρειο σέλας |
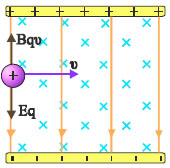 Σχ. 4.19 Φορτισμένο σωματίδιο εισέρχεται με ταχύτητα υ, σε χώρο όπου υπάρχει ηλεκτρικό και μαγνητικό πεδίο, κάθετα μεταξύ τους και κάθετα στην ταχύτητα του σωματιδίου. Σχ. 4.19 Φορτισμένο σωματίδιο εισέρχεται με ταχύτητα υ, σε χώρο όπου υπάρχει ηλεκτρικό και μαγνητικό πεδίο, κάθετα μεταξύ τους και κάθετα στην ταχύτητα του σωματιδίου. 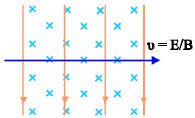 Σχ. 4.20 Από τα θετικά φορτισμένα σωματίδια της δέσμης μόνο όσα έχουν ταχύτητα υ=Ε/Β συνεχίζουν να κινούνται ευθύγραμμα ομαλά. Σχ. 4.20 Από τα θετικά φορτισμένα σωματίδια της δέσμης μόνο όσα έχουν ταχύτητα υ=Ε/Β συνεχίζουν να κινούνται ευθύγραμμα ομαλά.
|
4-9 ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΚΙΝΗΣΗΣ ΦΟΡΤΙΣΜΕΝΩΝ
ΣΩΜΑΤΙΔΙΩΝ ΕΠΙΛΟΓΕΑΣ ΤΑΧΥΤΗΤΩΝ
Ένα φορτισμένο σωματίδιο με μάζα m και φορτίο q εισέρχεται με ταχύτητα υ σε μια περιοχή όπου συνυπάρχουν ομογενές ηλεκτρικό και ομογενές μαγνητικό πεδίο, κάθετα μεταξύ τους. Η ταχύτητα του σωματιδίου είναι κάθετη στις δυναμικές γραμμές και των δύο πεδίων (σχ. 4.19). Το ηλεκτρικό πεδίο είναι κατακόρυφο προς τα κάτω ενώ το μαγνητικό πεδίο είναι κάθετο στο επίπεδο της σελίδας, με φορά προς τα μέσα. Αν το q είναι θετικό, από το ηλεκτρικό πεδίο δέχεται δύναμη μέτρου |q|E με φορά προς τα κάτω, ενώ από το μαγνητικό δύναμη B|q|υ με φορά προς τα πάνω. Εάν επιλέξουμε τις εντάσεις των πεδίων ώστε η ηλεκτρική δύναμη να εξισορροπείται από τη μαγνητική, το σωματίδιο θα συνεχίσει ανεπηρέαστο την πορεία του. Εξισώνοντας τη μαγνητική και την ηλεκτρική δύναμη (B|q|υ = E|q|), βρίσκουμε
δεν εκτρέπονται από το σύνθετο πεδίο. Αν όμως η δέσμη αποτελείται από φορτισμένα
θα συνεχίσουν την ευθύγραμμη πορεία τους (σχ. 4.20). Μια τέτοια διάταξη επιτρέπει να απομονώσουμε τα σωματίδια ορισμένης ταχύτητας και γι’ αυτό λέγεται «επιλογέας ταχυτήτων» ή «φίλτρο ταχυτήτων».
ΤΟ ΠΕΙΡΑΜΑ ΤΟΥ ΤHOMSON (ΤΟΜΣΟΝ) ΚΑΙ Η ΜΕΤΡΗΣΗ ΤΟΥ e/m
Αν και από την εποχή του Faraday υπέθεταν την ύπαρξη ηλεκτρικά φορτισμένων σωματιδίων μέσα στα άτομα, μόλις στο τέλος του προηγούμενου αιώνα (1897), ο J. J. Thomson απόδειξε πειραματικά την ύπαρξη ενός τέτοιου σωματιδίου, του ηλεκτρονίου. Το πείραμα του Thomson έγινε στο εργαστήριο του Cavendish του πανεπιστημίου του Cambridge, με μια συσκευή σαν αυτή που φαίνεται στο σχήμα 4.21.
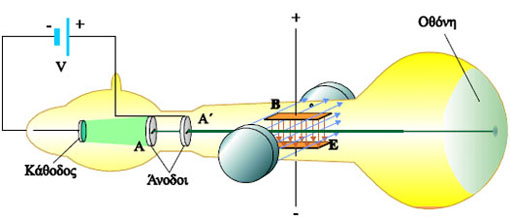 Σχ. 4.21 Σχ. 4.21 |
Μέσα σε ένα καθοδικό σωλήνα, στον οποίο επικρατεί υψηλό κενό, ηλεκτρόνια που προέρχονται από μια πυρακτωμένη κάθοδο, επιταχύνονται από τη διαφορά δυναμικού V ανάμεσα στην κάθοδο και τις ανόδους Α και Α΄ και σχηματίζουν μια δέσμη. Σύμφωνα με το θεώρημα έργου-ενέργειας η κινητική ενέργεια που θα αποκτήσουν τα ηλεκτρόνια είναι ίση με το έργο της δύναμης του ηλεκτρικού πεδίου
όπου e το φορτίο του ηλεκτρονίου κατ’ απόλυτη τιμή.
Η δέσμη των ηλεκτρονίων εισέρχεται σε ένα φίλτρο ταχυτήτων, σαν αυτό που περιγράψαμε προηγουμένως, και στη συνέχεια πέφτει σε μια οθόνη, στο άκρο του σωλήνα, η οποία είναι καλυμμένη με υλικό που φθορίζει. Στο σημείο που τα ηλεκτρόνια πέφτουν πάνω στην οθόνη το φθορίζον υλικό φωτοβολεί. Τα ηλεκτρόνια διέρχονται χωρίς απόκλιση από το φίλτρο ταχυτήτων μόνο όταν η ταχύτητά τους είναι υ = Ε/Β ή σύμφωνα με την (4.14) όταν
Οι ποσότητες E, V και B μπορούν να μετρηθούν και έτσι να προσδιοριστεί το πηλίκο e/m. Ο Thomson βρήκε ότι το πηλίκο αυτό έχει πάντοτε την ίδια τιμή, ανεξάρτητα από το υλικό της καθόδου ή οποιαδήποτε άλλη συνθήκη του πειράματος. Το γεγονός αυτό έδειξε ότι τα σωματίδια της δέσμης, τα οποία τώρα πια ονομάζονται ηλεκτρόνια, είναι κοινό συστατικό όλης της ύλης. Έτσι, στον Thomson αποδίδεται η ανακάλυψη του ηλεκτρονίου.
Ο Thomson απέδωσε τη μεγάλη τιμή του πηλίκου στη ΄΄μικρότητα της μάζας m ή στο μεγάλο φορτίο e, ή σε ένα συνδυασμό και των δύο΄΄. Δεκαπέντε χρόνια αργότερα ο Millikan υπολόγισε το στοιχειώδες ηλεκτρικό φορτίο. Η τιμή του e και η τιμή του πηλίκου που υπολόγισε ο Thomson έκαναν δυνατό τον προσδιορισμό της μάζας του ηλεκτρονίου. Μια αποδεκτή σήμερα τιμή της μάζας του ηλεκτρονίου είναι me=9,1093897x10-11 kg.
ΦΑΣΜΑΤΟΓΡΑΦΟΣ ΜΑΖΑΣ
Ο φασματογράφος μάζας είναι ένα όργανο που διαχωρίζει ιόντα που έχουν διαφορετικό πηλίκο μάζας προς φορτίο.
Ο πρώτος φασματογράφος μάζας, κατασκευάστηκε το 1919 από τον Francis Aston (Άστον), μαθητή του Τhomson. Στο σχήμα 4.22 φαίνεται μια παραλλαγή αυτού του φασματογράφου, που κατασκευάστηκε από τον Bainbridge (Μπέινμπριτζ) |
 Εικ. 4.10 J.J.Thomson (1856-1940). Αγγλία. Από τους σημαντικότερους φυσικούς της τελευταίας εκατονταετίας. Οι εργασίες του συνέβαλαν ουσιαστικά στην ανάπτυξη της σύγχρονης ατομικής φυσικής. Τιμήθηκε με το βραβείο Νόμπελ (1906). Εικ. 4.10 J.J.Thomson (1856-1940). Αγγλία. Από τους σημαντικότερους φυσικούς της τελευταίας εκατονταετίας. Οι εργασίες του συνέβαλαν ουσιαστικά στην ανάπτυξη της σύγχρονης ατομικής φυσικής. Τιμήθηκε με το βραβείο Νόμπελ (1906).
|
Σχ. 4.22 O φασματογράφος μάζας του Bainbridge χρησιμοποιεί ένα φίλτρο ταχυτήτων για την παραγωγή δέσμης ιόντων με την ίδια ταχύτητα. Στην περιοχή του μαγνητικού πεδίου B΄, τα ιόντα με τη μεγαλύτερη μάζα κινούνται σε τροχιά μεγαλύτερης ακτίνας.
|
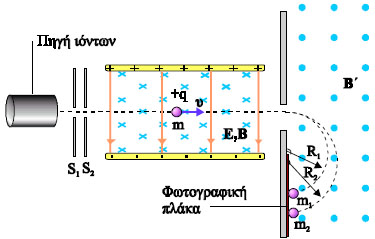 Ιόντα από μια πηγή περνούν μέσα από τις σχισμές S1 και S2 σχηματίζοντας μια λεπτή δέσμη. Στη συνέχεια τα ιόντα περνούν μέσα από ένα φίλτρο ταχυτήτων με πεδία Ε και Β, από όπου διέρχονται μόνο εκείνα που έχουν ταχύτητα
Τέλος, τα ιόντα εισέρχονται σε μια περιοχή όπου υπάρχει ομογενές μαγνητικό πεδίο B΄, κάθετο στην ταχύτητά τους. Το μαγνητικό πεδίο τα αναγκάζει να κινηθούν σε ημικυκλική τροχιά, ακτίνας R, μέχρι να πέσουν πάνω σε μια φωτογραφική πλάκα. Από το ίχνος που αφήνουν στη φωτογραφική πλάκα μας είναι γνωστή η ακτίνα της τροχιάς που διέγραψαν.
Από (4.15) και (4.16) προκύπτει
Η ακτίνα R υπολογίζεται από το ίχνος που αφήνουν τα ιόντα στη φωτογραφική πλάκα ενώ τα πεδία E, B και B' είναι γνωστά.
Δύο σωματίδια με ίδιο φορτίο αλλά με διαφορετική μάζα θα αφήσουν στη φωτογραφική πλάκα διαφορετικά ίχνη (σχ. 4.22). Ένα από τα πρώτα αποτελέσματα που έδωσε ο φασματογράφος μάζας ήταν ότι το νέον αποτελείται από δύο είδη ατόμων, με γραμμοατομικές μάζες 20g/mol και 22g/mol αντίστοιχα. Αυτό οφείλεται στο διαφορετικό αριθμό νετρονίων που έχουν στον πυρήνα τους τα δύο αυτά είδη ατόμων νέου. Άτομα των οποίων οι πυρήνες έχουν τον ίδιο αριθμό πρωτονίων (ατομικός αριθμός) αλλά διαφορετικό αριθμό νουκλεονίων δηλαδή, πρωτονίων και νετρονίων (μαζικό αριθμό), ονομάζονται ισότοπα. Μεταγενέστερα πειράματα έδειξαν ότι πολλά στοιχεία έχουν ισότοπα. Για παράδειγμα το χλώριο υπάρχει με μαζικό αριθμό 35 ( είναι και το 75% του χλωρίου στη φύση) και με μαζικό αριθμό 37 ( το 25%), ο άνθρακας με μαζικό 12 αλλά και με μαζικό 14 κ.ο.κ.
Στην πράξη, με τη σχέση (4.17), μετράμε τις μάζες των διαφόρων ισοτόπων ενός δεδομένου ιόντος με γνωστό φορτίο. Επίσης, μπορούμε να μετρήσουμε και τους λόγους των μαζών, ακόμη και εάν δε γνωρίζουμε το φορτίο. |
4-10 ΔΥΝΑΜΗ LAPLACE (ΛΑΠΛΑΣ)
Όπως είδαμε, ένα ηλεκτρικό φορτίο που κινείται μέσα σε μαγνητικό πεδίο δέχεται δύναμη από το πεδίο. Λογικό είναι να περιμένουμε ότι ένας ρευματοφόρος αγωγός που βρίσκεται μέσα σε μαγνητικό πεδίο θα δέχεται δύναμη από το πεδίο. Το ηλεκτρικό ρεύμα είναι το αποτέλεσμα της κίνησης πολλών φορτισμένων σωματιδίων μέσα στο αγωγό. Σε καθένα από αυτά τα σωματίδια το μαγνητικό πεδίο ασκεί δύναμη. Η συνολική δύναμη που δρα πάνω σε ένα αγωγό, είναι το μακροσκοπικό αποτέλεσμα των δυνάμεων που ασκεί το μαγνητικό πεδίο σε κάθε φορτισμένο σωματίδιο που κινείται μέσα στον αγωγό. Έτσι, μπορούμε, από τη δύναμη που δέχεται ένα σωματίδιο να υπολογίσουμε τη δύναμη που δέχεται ο ρευματοφόρος αγωγός. Ο υπολογισμός αυτός δίνεται στο τέλος της παραγράφου.
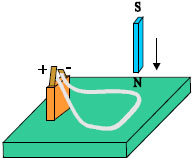
Το ότι το μαγνητικό πεδίο ασκεί δύναμη σε έναν αγωγό που διαρρέεται από ρεύμα, μπορούμε να το διαπιστώσουμε με τη διάταξη της εικόνας 4.11 Ένας οριζόντιος αγωγός ισορροπεί ανάμεσα στους πόλους ενός πεταλοειδούς μαγνήτη. Όταν ο αγωγός διαρρέεται από ρεύμα μετακινείται. Αν αντιστρέψουμε τη φορά του μαγνητικού πεδίου, ο αγωγός θα μετακινηθεί στην αντίθετη κατεύθυνση.
Η δύναμη που ασκεί το μαγνητικό πεδίο σε έναν αγωγό, ονομάζεται δύναμη Laplace.
Το μαγνητικό πεδίο ασκεί σε ευθύγραμμο ρευματοφόρο αγωγό που βρίσκεται μέσα σ΄ αυτό δύναμη
όπου φ η γωνία που σχηματίζει ο αγωγός με τις δυναμικές γραμμές, l το μήκος του αγωγού και Ι το ρεύμα που τον διαρρέει. Η δύναμη είναι κάθετη στο επίπεδο που ορίζεται από τον αγωγό και τις δυναμικές γραμμές και η φορά της δίνεται από τον κανόνα των τριών δακτύλων του δεξιού χεριού:
Σχηματίζουμε τρισορθογώνιο σύστημα με τα τρία δάκτυλα (αντίχειρας, δείκτης, μέσος) του δεξιού χεριού. Αν ο αντίχειρας δείχνει τη φορά του ρεύματος και ο δείκτης τη φορά του πεδίου, ο μέσος θα δείχνει τη φορά της δύναμης (εικ.4.12).
Από τη σχέση (4.18) προκύπτει ότι αν ο ρευματοφόρος αγωγός είναι παράλληλος στο μαγνητικό πεδίο (φ = 0ο ή φ = 180ο) δε δέχεται δύναμη από αυτό, ενώ αν είναι κάθετος στο μαγνητικό πεδίο (φ = 90ο) η δύναμη που δέχεται από το πεδίο παίρνει τη μέγιστη τιμή της F = BIl.
Αν ο αγωγός δεν είναι ευθύγραμμος, τον χωρίζουμε σε μικρά τμήματα, μήκους Δl, τόσο μικρά ώστε το καθένα από αυτά να μπορεί να θεωρηθεί ευθύγραμμο και υπολογίζουμε τη δύναμη που ασκείται σε κάθε ένα από αυτά. Η δύναμη που δέχεται ο αγωγός είναι η συνισταμένη αυτών των δυνάμεων.
|
 Εικ. 4.11 Όταν ο αγωγός που βρίσκεται ανάμεσα στους πόλους του μαγνήτη διαρρέεται από ρεύμα εκτρέπεται από τη θέση ισορροπίας του. Η εκτροπή του είναι αποτέλεσμα της δύναμης που δέχεται από το μαγνητικό πεδίο. Εικ. 4.11 Όταν ο αγωγός που βρίσκεται ανάμεσα στους πόλους του μαγνήτη διαρρέεται από ρεύμα εκτρέπεται από τη θέση ισορροπίας του. Η εκτροπή του είναι αποτέλεσμα της δύναμης που δέχεται από το μαγνητικό πεδίο. 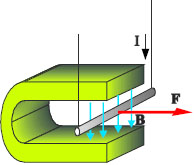 Σχ. 4.23 Η δύναμη Laplace που ασκεί το μαγνητικό πεδίο στον αγωγό είναι κάθετη στο επίπεδο που ορίζεται από τον αγωγό και τις δυναμικές γραμμές. Η φορά της δίνεται από τον κανόνα των τριών δακτύλων του δεξιού χεριού. Σχ. 4.23 Η δύναμη Laplace που ασκεί το μαγνητικό πεδίο στον αγωγό είναι κάθετη στο επίπεδο που ορίζεται από τον αγωγό και τις δυναμικές γραμμές. Η φορά της δίνεται από τον κανόνα των τριών δακτύλων του δεξιού χεριού.  Εικ. 4.12 Επεξήγηση του κανόνα των τριών δακτύλων του δεξιού χεριού για τη δύναμη Laplace. Εικ. 4.12 Επεξήγηση του κανόνα των τριών δακτύλων του δεξιού χεριού για τη δύναμη Laplace. |
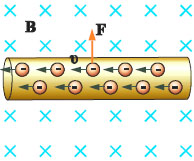 Σχ. 3.36 Ένα στοιχειώδες τμήμα ρευματοφόρου αγωγού μέσα σε ομογενές μαγνητικό πεδίο. Τα ηλεκτρόνια που κινούνται στον αγωγό δέχονται δύναμη από το μαγνητικό πεδίο. H δύναμη σημειώνεται ενδεικτικά πάνω σε ένα φορτίο. Σχ. 3.36 Ένα στοιχειώδες τμήμα ρευματοφόρου αγωγού μέσα σε ομογενές μαγνητικό πεδίο. Τα ηλεκτρόνια που κινούνται στον αγωγό δέχονται δύναμη από το μαγνητικό πεδίο. H δύναμη σημειώνεται ενδεικτικά πάνω σε ένα φορτίο.
|
Απόδειξη της σχέσης F = BIl ημφ Το κάθε φορτίο που κινείται μέσα στον αγωγό δέχεται δύναμη Bqυ ημφ Για να βρούμε τη δύναμη που δέχεται ο αγωγός θα πολλαπλασιάσουμε τη δύναμη που δέχεται κάθε φορτίο με το συνολικό αριθμό των φορέων φορτίου μέσα στον αγωγό. Αν n είναι οι φορείς φορτίου ανά μονάδα όγκου, επειδή ο όγκος του σύρματος είναι A·l (A : η διατομή του σύρματος), ο ολικός αριθμός φορέων φορτίου είναι nA·l . H ολική δύναμη που δέχεται ο αγωγός είναι
Όμως το γινόμενο nA qυ δίνει το ρεύμα που διαρρέει τον αγωγό. Πράγματι, η ταχύτητα των φορέων
Το γινόμενο ΑΔx δίνει τον όγκο του τμήματος του αγωγού μήκους Δx, οπότε το γινόμενο nΑΔx είναι ο ολικός αριθμός φορέων σ΄ αυτό το τμήμα του αγωγού και το qnΑΔx είναι το ολικό φορτίο ΔQ που μετακινείται στο τμήμα Δx του αγωγού
και η σχέση (4.19) γίνεται F = BIl ημφ Ορισμός του Β
Το Β ορίζεται από τη σχέση (4.18) στην περίπτωση που ο αγωγός είναι κάθετος στις δυναμικές γραμμές του πεδίου. Τότε ημφ = ημ90ο = 1 και
|
ΠΑΡΑΔΕΙΓΜΑ 4.3
Απάντηση: Επειδή το οριζόντιο τμήμα του βρόχου είναι κάθετο στο Β η δύναμη που δέχεται από το μαγνητικό πεδίο και την οποία μετράμε με το ζυγό είναι
|
4-11 ΜΑΓΝΗΤΙΚΗ ΔΥΝΑΜΗ ΑΝΑΜΕΣΑ ΣΕ ΔΥΟ
ΠΑΡΑΛΛΗΛΟΥΣ ΑΓΩΓΟΥΣ Στην προηγούμενη παράγραφο είδαμε ότι όταν ένας ρευματοφόρος αγωγός βρίσκεται μέσα σε μαγνητικό πεδίο δέχεται δύναμη από αυτό. Γνωρίζουμε επίσης ότι ένας αγωγός που διαρρέεται από ρεύμα δημιουργεί δικό του μαγνητικό πεδίο. Έτσι, αν τοποθετήσουμε κοντά δύο ρευματοφόρους αγωγούς, το μαγνητικό πεδίο του ενός θα ασκεί δύναμη στον άλλον.
Οι παράλληλοι αγωγοί του σχήματος 4.26 έχουν πολύ μεγάλο μήκος, διαρρέονται από ομόρροπα ρεύματα I1 και Ι2 και απέχουν μεταξύ τους απόσταση α . Ο αγωγός που διαρρέεται από ρεύμα Ι1, δημιουργεί, στην περιοχή που βρίσκεται ο αγωγός Ι2, μαγνητικό πεδίο Β1. Το Β1 είναι κάθετο στον αγωγό, όπως φαίνεται στο σχήμα 4.27 και το μέτρο του είναι
Σύμφωνα με το νόμο του Laplace, η μαγνητική δύναμη που δέχεται ένα τμήμα του δεύτερου αγωγού, μήκους l, επειδή βρίσκεται σε μαγνητικό πεδίο Β1, είναι
που, λόγω της (4.21), γίνεται
Μπορούμε να εκφράσουμε το αποτέλεσμα αυτό και ως δύναμη ανά μονάδα μήκους
Με τον κανόνα των τριών δακτύλων, βρίσκουμε ότι η δύναμη F2 κατευθύνεται προς τον πρώτο αγωγό. Με ανάλογο τρόπο βρίσκουμε και τη δύναμη F1 που ασκεί ο δεύτερος αγωγός σε τμήμα μήκους l του πρώτου. Η δύναμη αυτή είναι αντίθετη της F2. Όταν λοιπόν οι αγωγοί διαρρέονται από ομόρροπα ρεύματα έλκονται. Όταν τα ρεύματα είναι αντίρροπα οι αγωγοί απωθούνται. Επομένως
Παράλληλοι αγωγοί που διαρρέονται από ομόρροπα ρεύματα έλκονται, ενώ παράλληλοι αγωγοί που διαρρέονται από αντίρροπα ρεύματα απωθούνται. Το μέτρο της δύναμης με την οποία έλκονται ή απωθούνται δίνεται από τη σχέση (4.22)
Η δύναμη αυτή χρησιμοποιείται για να ορίσουμε τη μονάδα έντασης ηλεκτρικού ρεύματος το ampere, ως εξής:
1Α είναι το ρεύμα που όταν διαρρέει καθένα από δύο παράλληλους αγωγούς που βρίσκονται σε απόσταση 1m μεταξύ τους, ο ένας αγωγός ασκεί σε κάθε μέτρο του άλλου δύναμη 2x10-7 Ν. |
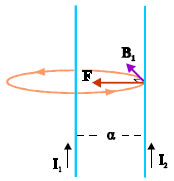 Σχ. 4.26 Ο αγωγός που διαρρέεται από ρεύμα έντασης Ι1, δημιουργεί μαγνητικό πεδίο που στα σημεία του δεύτερου αγωγού έχει ένταση Β1. Το μαγνητικό πεδίο Β1 ασκεί στο δεύτερο αγωγό δύναμη Laplace F. Σχ. 4.26 Ο αγωγός που διαρρέεται από ρεύμα έντασης Ι1, δημιουργεί μαγνητικό πεδίο που στα σημεία του δεύτερου αγωγού έχει ένταση Β1. Το μαγνητικό πεδίο Β1 ασκεί στο δεύτερο αγωγό δύναμη Laplace F.
|
ΠΑΡΑΔΕΙΓΜΑ 4.4
Επίπεδος πυκνωτής με χωρητικότητα C=5μF, συνδέεται με πηγή τάσης V=10V. Χωρίς να αποσυνδέσουμε τον πυκνωτή από την πηγή, εισάγουμε ανάμεσα στους οπλισμούς του μια πλάκα διηλεκτρικού, διηλεκτρικής σταθεράς Κ=5, που καταλαμβάνει ολόκληρο το χώρο μεταξύ των οπλισμών του. Να υπολογιστεί η αύξηση του φορτίου, που προκάλεσε η εισαγωγή του διηλεκτρικού.
Απάντηση:
Έστω ότι για να ισορροπεί ο δεύτερος αγωγός πρέπει να βρίσκεται σε απόσταση x από τον πρώτο. Ο πρώτος αγωγός ασκεί σε τμήμα του δεύτερου, μήκους l, ελκτική δύναμη
|
||||||||||||||||||
ΣΥΝΟΨΗ |
||||||||||||||||||||||
Νόμος των Biot και Savart. Ένα πολύ μικρό τμήμα Δl αγωγού που διαρρέεται από σταθερό ρεύμα Ι δημιουργεί σε ένα σημείο Α που απέχει απόσταση r από αυτό μαγνητικό πεδίο ΔB, μέτρου
όπου θ η γωνία ανάμεσα στο Δl και στο r. To μαγνητικό πεδίο ΔB είναι κάθετο στο επίπεδο που ορίζεται από τα Δl και r και η φορά του δίνεται από τον κανόνα του δεξιού χεριού. Νόμος του Ampère. Το άθροισμα των γινομένων B Δl συνθ κατά μήκος οποιασδήποτε κλειστής διαδρομής είναι ίσο με το γινόμενο μοΙεγκ, όπου Ιεγκ το συνολικό ρεύμα που διέρχεται από την επιφάνεια που ορίζει η κλειστή διαδρομή Νόμος του Gauss για το μαγνητισμό. Η μαγνητική ροή που διέρχεται από οποιαδήποτε κλειστή επιφάνεια είναι μηδέν.
Αν ένα φορτίο q κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο Β, το μαγνητικό πεδίο τού ασκεί δύναμη.
|
όπου φ η γωνία που σχηματίζει η ταχύτητα με το Β. Η δύναμη αυτή έχει διεύθυνση κάθετη στο επίπεδο που ορίζεται από τα υ και Β και φορά που δίνεται από τον κανόνα των τριών δακτύλων του δεξιού χεριού. Η δύναμη αυτή λέγεται δύναμη Lorentz. Όταν ένα φορτισμένο σωματίδιο κινείται κάθετα στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου κάνει ομαλή
Όταν εισέρχεται με τυχαία γωνία σε ομογενές μαγνητικό πεδίο κάνει ελικοειδή κίνηση. Ευθύγραμμος αγωγός μήκους l, που διαρρέεται από ρεύμα έντασης Ι και βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο, δέχεται δύναμη
Η δύναμη αυτή ονομάζεται δύναμη Laplace, έχει διεύθυνση κάθετη στο επίπεδο που ορίζεται από τον αγωγό και τις δυναμικές γραμμές και φορά που δίνεται από τον κανόνα των τριών δακτύλων του δεξιού χεριού. Όταν δύο παράλληλοι ευθύγραμμοι αγωγοί απείρου μήκους διαρρέονται από ρεύμα, ο ένας αγωγός ασκεί στον άλλο δύναμη. Η δύναμη που δέχεται κάθε αγωγός ανά μονάδα μήκους του είναι
Η δύναμη είναι ελκτική αν οι αγωγοί διαρρέονται από ομόρροπα ρεύματα και απωστική αν διαρρέονται από αντίρροπα ρεύματα. Αν η ανά μονάδα μήκους δύναμη που ασκείται σε κάθε έναν από δύο παράλληλους ευθύγραμμους αγωγούς μεγάλου μήκους που διαρρέονται από το ίδιο ρεύμα και βρίσκονται σε απόσταση 1m μεταξύ τους, είναι 2x10-7 Ν/m, τότε, εξ ορισμού, η ένταση του ρεύματος που διαρρέει κάθε αγωγό είναι 1Α. |
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ |
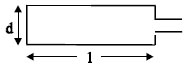
1. Το μαγνητικό πεδίο στο κέντρο ενός πλαισίου
|
 Σχ. 4.28 Σχ. 4.28
 Σχ. 4.29 Σχ. 4.29
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
ΕΡΩΤΗΣΕΙΣ |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Σχ. 4.31 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 Σχ. 4.32 Σχ. 4.32 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Σχ. 4.34 Σχ. 4.34 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 Σχ. 4.35 Σχ. 4.35
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
ΑΣΚΗΣΕΙΣ |
 |
|
|||||||||||||||||||||||||||
|
 Σχ. 4.40 Σχ. 4.40
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
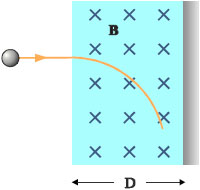 Σχ. 4.41 Σχ. 4.41
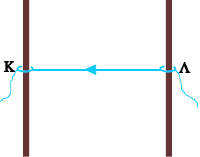 Σχ. 4.42 Σχ. 4.42 |
|
||||||||||||||||||||||||||
|
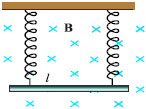 Σχ. 4.43 Σχ. 4.43
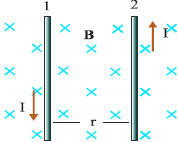 Σχ. 4.44 Σχ. 4.44 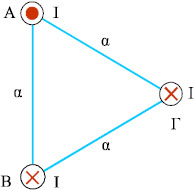 Σχ. 4.45 Σχ. 4.45 |
|||||||||||||||||||||||||||||||||
ΠΡΟΒΛΗΜΑΤΑ |
 Σχ. 4.46 Σχ. 4.46
 Σχ. 4.47 Σχ. 4.47
 Σχ. 4.48 Σχ. 4.48 |
|
||||||||||||||||||||||||||||||||||||
|
 χ. 4.49 χ. 4.49
 χ. 4.50 χ. 4.50 |

|
TO ΦΑΙΝΟΜΕΝΟ HALL (Χολ) To 1879 o Edwin Hall διαπίστωσε ότι σε ένα πλακίδιο που διαρρέεται από ρεύμα, τοποθετημένο μέσα σε μαγνητικό πεδίο, δημιουργείται διαφορά δυναμικού σε διεύθυνση που είναι κάθετη στο ρεύμα και στο μαγνητικό πεδίο. Το φαινόμενο αυτό, που είναι γνωστό ως φαινόμενο Ηall οφείλεται στην απόκλιση που υφίστανται οι φορείς του ρεύματος, εξ αιτίας της δύναμης που δέχονται από το μαγνητικό πεδίο.
Η ανάλυση των αποτελεσμάτων του φαινομένου Ηall σε ένα αγώγιμο πλακίδιο δίνει πληροφορίες για τους φορείς του ηλεκτρικού ρεύματος και για την πυκνότητά τους. Το φαινόμενο το εκμεταλλευόμαστε στη μέτρηση μαγνητικών πεδίων.
Έστω ένας αγωγός σε σχήμα πλάκας που διαρρέεται από ρεύμα κατά τη θετική κατεύθυνση του άξονα x. Στην κατεύθυνση y υπάρχει ομογενές μαγνητικό πεδίο Β. Εάν οι φορείς του ηλεκτρικού ρεύματος είναι ελεύθερα ηλεκτρόνια, (σχ. 4.51α) αυτά θα κινούνται προς την αρνητική κατεύθυνση του άξονα x με μια μέση ταχύτητα υd (ταχύτητα διολίσθησης). Στα ηλεκτρόνια αυτά το μαγνητικό πεδίο ασκεί δύναμη F με κατεύθυνση προς τα επάνω, και συνεπώς αποκλίνουν από την πορεία τους και συσσωρεύονται στο επάνω μέρος της πλάκας. Με τη συσσώρευση των ηλεκτρονίων στο επάνω μέρος της πλάκας δημιουργείται περίσσεια θετικού φορτίου στο κάτω μέρος της. Η συσσώρευση ίσων ποσοτήτων θετικού και αρνητικού φορτίου στο κάτω και επάνω μέρος της πλάκας συνεπάγεται τη δημιουργία στο εσωτερικό της πλάκας ομογενούς ηλεκτρικού πεδίου το οποίο ασκεί στα ελεύθερα ηλεκτρόνια δύναμη Εq, με φορά προς τα κάτω. H συσσώρευση ηλεκτρικού φορτίου συνεχίζεται μέχρις ότου η ηλεκτρική δύναμη Εq εξισορροπήσει τη μαγνητική δύναμη F. 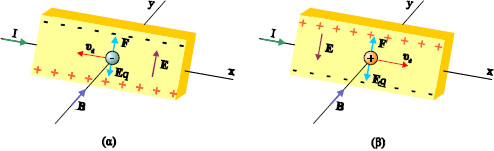 Σχ. 4.51 Σχ. 4.51 |
Με ένα ευαίσθητο γαλβανόμετρο μπορούμε να μετρήσουμε τη διαφορά δυναμικού που δημιουργείται μεταξύ του κάτω και του επάνω μέρους της πλάκας εξαιτίας της συσσώρευσης ηλεκτρικού φορτίου. Αυτή η διαφορά δυναμικού ονομάζεται τάση Ηall (VH). Εάν οι φορείς του ηλεκτρικού ρεύματος είναι θετικοί, (όπως συμβαίνει σε ορισμένους ημιαγωγούς) (σχ. 4.51β) αυτοί θα εκτραπούν προς τα πάνω και έτσι στο επάνω μέρος συσσωρεύεται θετικό φορτίο ενώ στο κάτω αρνητικό. Στην περίπτωση αυτή το πρόσημο της τάσης Ηall είναι αντίθετο από ότι πριν, όταν οι φορείς ήταν ηλεκτρόνια. Προσδιορίζοντας λοιπόν την πολικότητα της τάσης Ηall προσδιορίζεται το πρόσημο των φορέων φορτίου. Μπορούμε να βρούμε μια έκφραση για την τάση Ηall αν θυμηθούμε ότι στην κατάσταση ισορροπίας η δύναμη του μαγνητικού πεδίου εξισορροπείται από τη δύναμη του ηλεκτρικού πεδίου Eq
Από τη σχέση (4.24) παρατηρούμε ότι αν γνωρίζουμε την τάση Hall το Β και το d, μπορούμε να υπολογίσουμε την ταχύτητα διολίσθησης των φορέων του ρεύματος. Η ένταση του ρεύματος μπορεί να εκφρασθεί και ως συνάρτηση του αριθμού n των φορέων φορτίου ανά μονάδα όγκου, όπως υπολογίστηκε στη σχέση (4.20) Ας πάρουμε την περίπτωση όπου η ηλεκτρική δύναμη είναι αρκετά μεγάλη και το σταγονίδιο κινείται προς τα πάνω, τότε η αντίσταση F, κατευθύνεται προς τα κάτω. Αν υ΄ είναι η νέα οριακή ταχύτητα που θα αποκτήσει η σταγόνα, ισχύει
όπου Α το εμβαδόν της διατομής της πλάκας. Θέτοντας στη σχέση (4.24) την (4.25) βρίσκουμε
Από τη σχέση αυτή μπορούμε να υπολογίσουμε την πυκνότητα φορέων ρεύματος του αγωγού. To φαινόμενο Hall έχει πολλές πρακτικές εφαρμογές σε διάφορους χώρους, μεταξύ αυτών και στην ιατρική. Το αίμα περιέχει ιόντα τα οποία κινούνται με την ταχύτητα ροής του. Μπορούμε να θεωρήσουμε την κίνηση των ιόντων σαν ηλεκτρικό ρεύμα. Εφαρμόζουμε ένα μαγνητικό πεδίο κάθετα σε μια αρτηρία και μετράμε την τάση Hall που αναπτύσσεται στα τοιχώματά της. Από τη σχέση που δίνει τη τάση Hall μπορούμε να υπολογίσουμε την ένταση του ρεύματος και στη συνέχεια από τη σχέση (4.25) την ταχύτητα των ιόντων που είναι και η ταχύτητα ροής του αίματος. Γνωρίζοντας την ταχύτητα ροής του αίματος στην αρτηρία οι γιατροί μπορούν να βγάλουν συμπεράσματα για την κατάσταση του κυκλοφορικού συστήματος του ασθενή. |
|