2.2 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ

Η Εξίσωση Ax + By + Γ =0, με Α 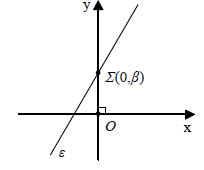0 ή Β 0

• Έστω ε μια ευθεία στο καρτεσιανό επίπεδο.
— Αν η ευθεία ε τέμνει τον άξονα yy' στο σημείο Σ(0,β) και έχει συντελεστή διεύθυνσης λ, τότε θα έχει εξίσωση η οποία γράφεται

• Αν η ευθεία ε είναι κατακόρυφη και διέρχεται από το σημείο P(x₀,y₀), τότε θα έχει εξίσωση x=x₀, η οποία γράφεται ισοδύναμα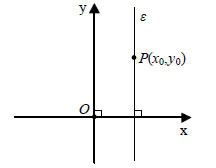

Βλέπουμε, δηλαδή, ότι και στις δύο περιπτώσεις η εξίσωση της ευθείας ε παίρνει τη μορφή Ax + By + Γ =0 με

• Αντιστρόφως, έστω η εξίσωση με Ax + By + Γ =0 με
— Αν τότε η εξίσωση γράφεται , που είναι εξίσωση ευθείας με συντελεστή διεύθυνσης και η οποία τέμνει τον άξονα yy' στο σημείο
— Αν B=0, τότε, λόγω της υπόθεσης, είναι και η εξίσωση γράφεται που είναι εξίσωση ευθείας κάθετης στον άξονα x'x στο σημείο του .

Σε όλες λοιπόν τις περιπτώσεις η εξίσωση παριστάνει ευθεία. Αποδείξαμε, δηλαδή, ότι ισχύει το επόμενο θεώρημα:

ΘΕΩΡΗΜΑ

Κάθε ευθεία του επιπέδου έχει εξίσωση της μορφής

                                  (1)

και αντιστρόφως, κάθε εξίσωση της μορφής (1) παριστάνει ευθεία γραμμή.

Για παράδειγμα, η εξίσωση 2x + y -6 = 0 παριστάνει ευθεία. Η εξίσωση αυτή γράφεται στη μορφή y= - 2x +6 και βλέπουμε ότι έχει συντελεστή διεύθυνσης λ= -2 και τέμνει τον άξονα yy' στο σημείο (0,6).

Διάνυσμα Παράλληλο ή Κάθετο σε Ευθεία

Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία του επιπέδου με εξίσωση Ax +By + Γ =0 . Είδαμε προηγουμένως ότι:

— Αν τότε η ε έχει συντελεστή διεύθυνσης και επομένως είναι παράλληλη προς το διάνυσμα

— Αν B=0, τότε η ε είναι παράλληλη προς τον άξονα yy' και επομένως παράλληλη και πάλι προς το διάνυσμα Σε κάθε περίπτωση λοιπόν ισχύει ότι:

Η ευθεία με εξίσωση Ax +By + Γ =0 είναι παράλληλη στο διάνυσμα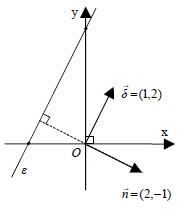

Όμως, το διάνυσμα είναι κάθετο στο διάνυσμα , αφού

Επομένως:

Η ευθεία με εξίσωση Ax +By + Γ =0 είναι κάθετη στο διάνυσμα .

Για παράδειγμα, η ευθεία 2x -y +4 = 0 είναι παράλληλη στο διάνυσμα και κάθετη στο διάνυσμα

ΕΦΑΡΜΟΓΕΣ

1. Δίνεται η εξίσωση:

(i) Να αποδειχτεί ότι

—Για κάθε τιμή της παραμέτρου λ η εξίσωση (1) παριστάνει ευθεία γραμμή

—Όλες οι ευθείες που ορίζονται από την εξίσωση (1) (Οικογένεια ευθειών) διέρχονται από το ίδιο σημείο.

(ii) Ποια από τις παραπάνω ευθείες είναι κάθετη στην ευθεία ζ : y = 2x;

ΑΠΟΔΕΙΞΗ

(i) Η εξίσωση (1) γράφεται ισοδύναμα

Επειδή δεν υπάρχει τιμή του λ για την οποία να μηδενίζονται και ο συντελεστής του x και ο συντελεστής του y, η εξίσωση (2) παριστάνει ευθεία για κάθε τιμή του

Για να δείξουμε ότι όλες οι ευθείες της οικογένειας (1) διέρχονται από το ίδιο σημείο, αρκεί να βρούμε ένα σημείο K(x₀,y₀) του οποίου οι συντεταγμένες να επαληθεύουν την (1) για όλες τις τιμές του λ. Το ζητούμενο σημείο θα είναι εκείνο του οποίου οι συντεταγμένες μηδενίζουν τις παραστάσεις , δηλαδή η λύση του συστήματος

Από την επίλυση του συστήματος βρίσκουμε ότι x₀= -3 και y₀= 1. Επομένως, όλες οι ευθείες της οικογένειας (1) διέρχονται από το σημείο K(-3,1).

(ii) Έστω ε ευθεία της οικογένειας (1) που είναι κάθετη στην ευθεία ζ. Τότε θα ισχύει

όμως, λόγω της (2), ο συντελεστής διεύθυνσης της ευθείας ε είναι ίσος με

Επομένως, από την (3) έχουμε

οπότε η ευθεία ε θα έχει εξίσωση -2x -4y -2= 0 που γράφεται

2. Δίνεται τρίγωνο ΑΒΓ με κορυφές Α(2,3), Β(4,1) και Γ(5λ-1,λ), . Να αποδείξετε ότι το κέντρο βάρους του τριγώνου κινείται σε μια ευθεία, καθώς το λ μεταβάλλεται στο R.

ΛΥΣΗ

Αν G(x,y) το κέντρο βάρους του τριγώνου, τότε και Έχουμε λοιπόν το σύστημα

Απαλείφουμε το λ από τις εξισώσεις και βρίσκουμε 3x -15y + 15=0 ή ισοδύναμα x -5y +5 =0. Άρα, το κέντρο βάρους του τριγώνου ABΓ κινείται στην ευθεία x -5y +5 =0.

3. Να βρεθεί η οξεία γωνία των ευθειών ε₁ : x - y +1 =0 και ε₂ : 2x + y -3 =0.

ΛΥΣΗ

Οι ευθείες ε₁ και ε₂ έχουν συντελεστές διεύθυνσης λ₁ = 1 και λ₂= -2. Άρα, είναι παράλληλες προς τα διανύσματα και . Επομένως, η οξεία γωνία θ των ευθειών ε₁ και ε₂ είναι ίση ή παραπληρωματική της γωνίας φ των διανυσμάτων . Όμως, είναι:

Επομένως , οπότε .

Ασκήσεις