1.2 ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

Πρόσθεση Διανυσμάτων

Έστω δύο διανύσματα Με αρχή ένα σημείο Ο παίρνουμε διάνυσμα και στη συνέχεια με αρχή το Α παίρνουμε διάνυσμα Τοδιάνυσμα λέγεται άθροισμα ή συνισταμένη των διανυσμάτων και συμβολίζεται με .

Θα αποδείξουμε ότι το άθροισμα των διανυσμάτων 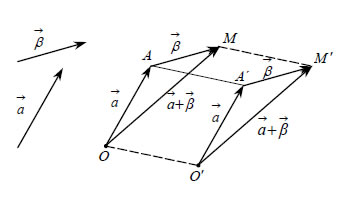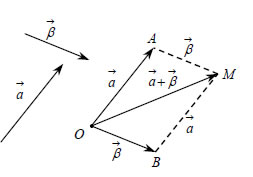είναι ανεξάρτητοτης επιλογής του σημείου Ο. Πράγματι, αν O' είναι ένα άλλο σημείο καιπάρουμε τα διανύσματα και , επειδή και , έχουμε και . Επομένως, , που συνεπάγεται ότι και .

Το άθροισμα δύο διανυσμάτων βρίσκεταικαι με το λεγόμενο κανόνα τουπαραλληλόγραμμου. Δηλαδή, αν με αρχήένα σημείο Ο πάρουμε τα διανύσματα και , τότε το άθροισμα ορίζεται από τη διαγώνιο OMτου παραλληλόγραμμου που έχειπροσκείμενες πλευρές τις OA και OB.

Ιδιότητες Πρόσθεσης Διανυσμάτων

Για την πρόσθεση των διανυσμάτων ισχύουν οι γνωστές ιδιότητες τηςπρόσθεσης πραγματικών αριθμών. Δηλαδή, αν είναι τρία διανύσματα,τότε:

(1)     (Αντιμεταθετική ιδιότητα)

(2)     (Προσεταιριστική ιδιότητα)

(3)    

(4)    

ΑΠΟΔΕΙΞΗ

• Από το προηγούμενο σχήμα έχουμε: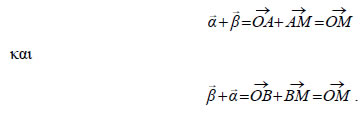

Επομένως, .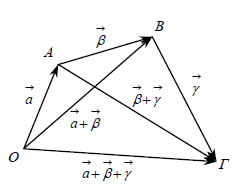

• Από το διπλανό σχήμα έχουμε: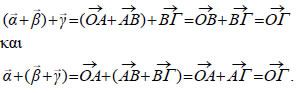

Επομένως,

• Οι ιδιότητες (3) και (4) είναι προφανείς.    

Η προσεταιριστική ιδιότητα μας επιτρέπει να συμβολίζουμε καθένα από τα ίσααθροίσματα και με ,το οποίο θα λέμεάθροισμα των τριών διανυσμάτων . Το άθροισμα περισσότερωνδιανυσμάτων ορίζεται επαγωγικά ως εξής:

Για παράδειγμα,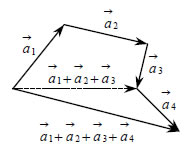

Δηλαδή, για να προσθέσουμε ν διανύσματα τα καθιστούμεδιαδοχικά, οπότε το άθροισμά τους θα είναι το διάνυσμα που έχει ως αρχή τηναρχή του πρώτου και ως πέρας το πέρας του τελευταίου. Επειδή μάλισταισχύουν η αντιμεταθετική και η προσεταιριστική ιδιότητα της πρόσθεσης, τοάθροισμα δε μεταβάλλεται αν αλλάξει η σειρά των προσθετέων ή αν μερικοίαπό αυτούς αντικατασταθούν με το άθροισμά τους.

Αφαίρεση Διανυσμάτων

Η διαφορά 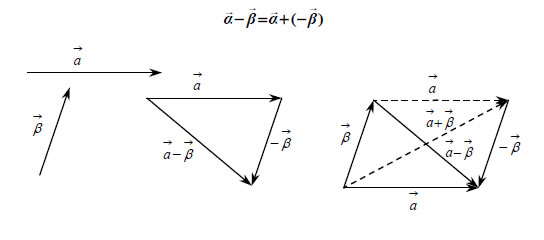του διανύσματος από το διάνυσμα ορίζεται ωςάθροισμα των διανυσμάτων και - . Δηλαδή

Σύμφωνα με τα παραπάνω, αν έχουμε δύο διανύσματα και , τότε υπάρχειμοναδικό διάνυσμα , τέτοιο, ώστε . Πράγματι,

Διάνυσμα Θέσεως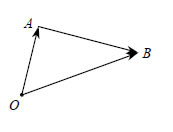

Έστω Ο ένα σταθερό σημείο του χώρου. Τότε γιακάθε σημείο Μ του χώρου ορίζεται το διάνυσμα , το οποίο λέγεται διάνυσμα θέσεως του Μ ήδιανυσματική ακτίνα του Μ. Το σημείο Ο, που είναιη κοινή αρχή όλων των διανυσματικών ακτίνων τωνσημείων του χώρου, λέγεται σημείο αναφοράς στοχώρο.

Αν Ο είναι ένα σημείο αναφοράς, τότε για οποιοδήποτε διάνυσμα 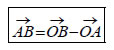έχουμε και επομένως

Δηλαδή:

"Κάθε διάνυσμα στο χώρο είναι ίσο με τη διανυσματική ακτίνα τουπέρατος μείον τη διανυσματική ακτίνα της αρχής".

Μέτρο Αθροίσματος Διανυσμάτων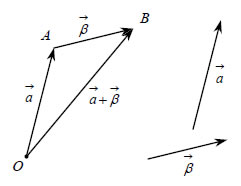

Στο διπλανό σχήμα βλέπουμε τοάθροισμα των διανυσμάτων 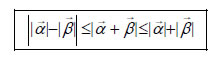.Από την τριγωνική ανισότητα γνωρίζουμεόμως ότι

και επομένως

ΕΦΑΡΜΟΓΕΣ

1. Για τέσσερα σημεία Α, Β, Γ, Δ να αποδειχτεί ότι

ΑΠΟΔΕΙΞΗ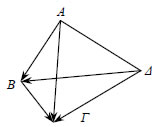

Αν Ο είναι ένα σημείο αναφοράς, τότε έχουμε:

2. Να αποδειχτεί ότι

ΑΠΟΔΕΙΞΗ

Έχουμε

Ασκήσεις