1ΔΙΑΝΥΣΜΑΤΑ Εισαγωγή Το διάνυσμα είναι ένα χαρακτηριστικό παράδειγμα έννοιας που αναπτύχθηκεμέσα από τη στενή αλληλεπίδραση Μαθηματικών και Φυσικής. Ο "κανόναςτου παραλληλόγραμμου", σύμφωνα με τον οποίο το μέτρο και η κατεύθυνσηδύο δυνάμεων που ασκούνται σε ένα σώμα εκφράζονται από τη διαγώνιο τουπαραλληλόγραμμου που σχηματίζουν, ήταν γνωστός με διάφορες μορφές στουςΑρχαίους Έλληνες επιστήμονες. Ο Ήρων ο Αλεξανδρεύς, για παράδειγμα, στοέργο του "Μηχανικά" αποδεικνύει με χρήση αναλογιών την ακόλουθηγεωμετρική πρόταση: 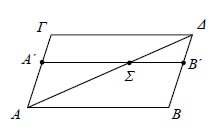 Αν ένα σημείο Σ κινείται με ομαλή κίνησηκατά μήκος μιας ευθείας ΑΒ, ενώ συγχρόνως ηΑΒ κινείται παράλληλα προς τον εαυτό της μετο άκρο Α να διαγράφει μια ευθεία ΑΓ, τότε ηπραγματική τροχιά του Σ (η "συνισταμένηκίνηση") θα είναι η διαγώνιος ΑΔ τουπαραλληλόγραμμου ΑΒΓΔ. Αυτός ο "κανόνας" χρησιμοποιήθηκε πολλούς αιώνες για το γεωμετρικόπροσδιορισμό της συνισταμένης, χωρίς όμως να θεωρείται ένα νέο είδοςπρόσθεσης ευθυγράμμων τμημάτων, διαφορετικό από εκείνο πουχρησιμοποιείται στην Ευκλείδεια Γεωμετρία. Για να γίνει αυτό, χρειάστηκε απότη μια μεριά η αποδοχή και συστηματική χρήση των αρνητικών αριθμών σταΜαθηματικά και από την άλλη η μελέτη φυσικών ποσοτήτων όπως η ταχύτητα,η δύναμη, η ορμή και η επιτάχυνση, που χαρακτηρίζονται τόσο από το μέτροόσο και από τη διεύθυνσή τους. Αυτές οι εξελίξεις έφεραν στο προσκήνιο τιςέννοιες της προσανατολισμένης κίνησης και του προσανατολισμένουευθύγραμμου τμήματος, τις πρώτες ιδέες των οποίων συναντάμε σε έργαεπιστημόνων του 17ου αιώνα όπως οι J. Wallis, I. Newton και G.W. Leibniz. Η ανάπτυξη ενός συστηματικού λογισμού με προσανατολισμένα ευθύγραμματμήματα άρχισε στα τέλη του 18ου αιώνα, για να δοθεί μια γεωμετρικήερμηνεία στους αρνητικούς αριθμούς, αλλά και για να βρεθεί ένας τρόποςαναλυτικής έκφρασης του μήκους και της διεύθυνσης των ευθύγραμμωντμημάτων. Πρωτοποριακό υπήρξε προς αυτή την κατεύθυνση το έργο των C.Wessel (1799) και R. Argand (1806). Ξεκινώντας από την απλή περίπτωση των |
προσανατολισμένων τμημάτων που βρίσκονται στην ίδια ευθεία, προχώρησανστον ορισμό των πράξεων με τυχαία τμήματα του επιπέδου. Συγκεκριμένα, οιορισμοί του Wessel ήταν οι εξής:
Στις εργασίες των Wessel και Argand (και ορισμένες άλλες που δημοσιεύτηκανεκείνη την εποχή) υπάρχουν οι βασικές ιδέες που συγκροτούν σήμερα τοΔιανυσματικό Λογισμό του επιπέδου. Η ουσιαστική ανάπτυξη του κλάδουαρχίζει όμως μερικές δεκαετίες αργότερα, όταν επιχειρείται η γενίκευση αυτώντων ιδεών στον τρισδιάστατο χώρο και η θεμελίωση μιας γενικής μαθηματικήςθεωρίας. Καθοριστικό υπήρξε προς αυτήν την κατεύθυνση του έργο του W.Hamilton (1843) και του H. Grassmann (1844). Ο W. Hamilton χρησιμοποίησετον όρο διάνυσμα (vector). Ο όρος vector προέρχεται κατά μία εκδοχή από τολατινικό ρήμα "vehere" που σημαίνει μεταφέρω. Ο H. Grassmannχρησιμοποίησε τους όρους εσωτερικό και εξωτερικό γινόμενο. Η παραπέρα εξέλιξη του Διανυσματικού Λογισμού επηρεάστηκε αποφασιστικάαπό τις εξελίξεις στη Φυσική κατά το δεύτερο μισό του 19ου αιώνα. Η χρήσητης θεωρίας του Hamilton από τον ιδρυτή της ηλεκτρομαγνητικής θεωρίας J.C.Maxwell (1873) οδήγησε σε ορισμένες τροποποιήσεις, με βάση τις οποίες οιφυσικοί J.W. Gibbs και O. Heaviside δημιούργησαν στις αρχές της δεκαετίαςτου 1880 τη σύγχρονη θεωρία του Διανυσματικού Λογισμού (στοιχεία τηςοποίας παρουσιάζονται σ' αυτό το κεφάλαιο). Τέλος το 1888, ο G. Peano, μεβάση τη θεωρία του Grassmann θεμελίωσε αξιωματικά την έννοια τουδιανυσματικού χώρου. 1.1 Η ΕΝΝΟΙΑ ΤΟΥ ΔΙΑΝΥΣΜΑΤΟΣ |
Ορισμός του Διανύσματος Υπάρχουν μεγέθη, όπως είναι η μάζα, ο όγκος, η πυκνότητα, η θερμοκρασίακτλ., τα οποία προσδιορίζονται από το μέτρο τους και από την αντίστοιχημονάδα μέτρησης. Τα μεγέθη αυτά λέγονται μονόμετρα ή βαθμωτά. Υπάρχουν όμως και μεγέθη, όπως είναι η δύναμη, η ταχύτητα, η επιτάχυνση, ημετατόπιση, η μαγνητική επαγωγή κτλ., που για να τα προσδιορίσουμε, εκτόςαπό το μέτρο τους και τη μονάδα μέτρησης, χρειαζόμαστε τη διεύθυνση και τηφορά τους. Τέτοια μεγέθη λέγονται διανυσματικά μεγέθη ή απλώςδιανύσματα. 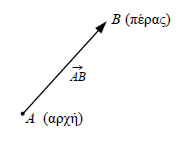 • Στη Γεωμετρία το διάνυσμα ορίζεται ως έναπροσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ωςένα ευθύγραμμο τμήμα του οποίου τα άκραθεωρούνται διατεταγμένα. Το πρώτο άκρο λέγεταιαρχή ή σημείο εφαρμογής του διανύσματος, ενώ τοδεύτερο λέγεται πέρας του διανύσματος. Τοδιάνυσμα με αρχή το Α και πέρας το Β συμβολίζεταιμε Αν η αρχή και το πέρας ενός διανύσματος συμπίπτουν, τότε το διάνυσμαλέγεται μηδενικό διάνυσμα. Έτσι, για παράδειγμα, το διάνυσμα Για το συμβολισμό των διανυσμάτων χρησιμοποιούμε πολλές φορές τα μικράγράμματα του ελληνικού ή του λατινικού αλφάβητου επιγραμμισμένα με βέλος για παράδειγμα, • Η απόσταση των άκρων ενός διανύσματος 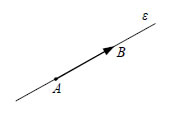 Αν το διάνυσμα • Η ευθεία πάνω στην οποία βρίσκεται ένα μημηδενικό διάνυσμα |
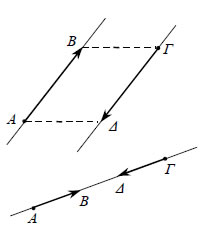
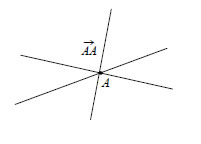 Ως φορέα ενός μηδενικού διανύσματος Αν ο φορέας ενός διανύσματος 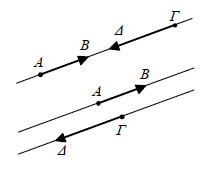 • Δύο μη μηδενικά διανύσματα Τα συγγραμμικά διανύσματα διακρίνονται σε ομόρροπα και αντίρροπα.Συγκεκριμένα: 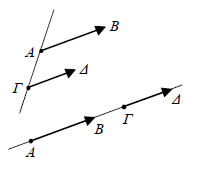 - Δύο μη μηδενικά διανύσματα α) όταν έχουν παράλληλους φορείς καιβρίσκονται στο ίδιο ημιεπίπεδο ως προς τηνευθεία ΑΓ που ενώνει τις αρχές τους ή β) όταν έχουν τον ίδιο φορέα και μία από τιςημιευθείες ΑΒ και ΓΔ περιέχει την άλλη. Στηνπερίπτωση αυτή λέμε ότι τα |
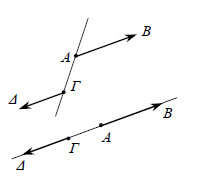 - Δύο μη μηδενικά διανύσματα Ίσα Διανύσματα 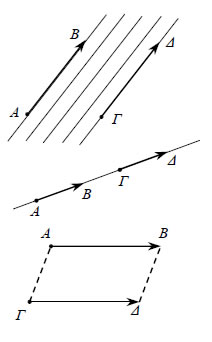 Δύο μη μηδενικά διανύσματα λέγονται ίσα ότανέχουν την ίδια κατεύθυνση και ίσα μέτρα. Για ναδηλώσουμε ότι δύο διανύσματα Εύκολα αποδεικνύεται ότι: • Αν • Αν Μ είναι το μέσον του ΑΒ, τότε 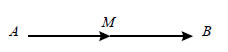 Αντίθετα Διανύσματα Δύο διανύσματα λέγονται αντίθετα, όταν έχουν αντίθετη κατεύθυνση και ίσαμέτρα. Για να δηλώσουμε ότι δύο διανύσματα |
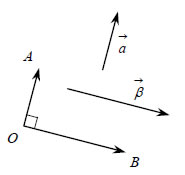
 Γωνία δύο Διανυσμάτων Έστω δύο μη μηδενικά διανύσματα Την κυρτή γωνία • θ = 0, αν • θ = π, αν |
 Αν Αν ένα από τα διανύσματα ΕΦΑΡΜΟΓΗ 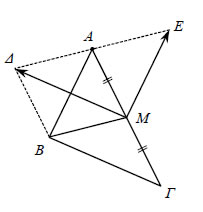 Έστω Μ το μέσο της πλευράς ΑΓ ενός τριγώνου ΑΒΓ. Με αρχή το Μ γράφουμε ταδιανύσματα ΑΠΟΔΕΙΞΗ Αρκεί να δείξουμε ότι Όμως το Μ είναι μέσο του ΑΓ. Άρα, Επομένως, λόγω των (1) και (2), έχουμε Επειδή επιπλέον Έτσι, από τις σχέσεις (3) και (4) έχουμε |