ΠΡΟΒΟΛΕΣ
9.3 Παράσταση αντικειμένου 9.3.1 Ποιες προβολές χρησιμοποιούμε στο Σχέδιο Από τις άπειρες δυνατότητες προβολών που μας παρέχει η Παραστατική Γεωμετρία, στο τεχνικό σχέδιο χρησιμοποιούμε ένα μικρό αριθμό προβολών, ανάλογα με το αποτέλεσμα που επιδιώκουμε. Οι κεντρικές προβολές μας παρέχουν εικόνες που έχουν σχέση με τη φωτογραφική απεικόνιση ενός αντικειμένου και δεν είναι κατάλληλες για λήψη τεχνικών πληροφοριών (μετρήσεις και υπολογισμούς μεγεθών). Χρησιμοποιούνται όμως στο αρχιτεκτονικό σχέδιο για την απεικόνιση του χώρου και έχουν, κατά κύριο λόγο, εικαστικό χαρακτήρα. Από τις παράλληλες προβολές χρησιμοποιούμε κυρίως τις ορθές και έναν πολύ περιορισμένο αριθμό από τις πλάγιες προβολές.
9.3.2 Ορθές προβολές
I. Παράσταση σε ένα επίπεδο προβολής Από όσα παρατέθηκαν προηγουμένως στην παρ. 9.2.2,1, βγάζουμε το συμπέρασμα ότι μπορούμε να παραστήσουμε τη μορφή ενός αντικειμένου μέσω μιας προβολής του (εικ. 9.8 - 9.11):
εικ. 9.8 - 9.11 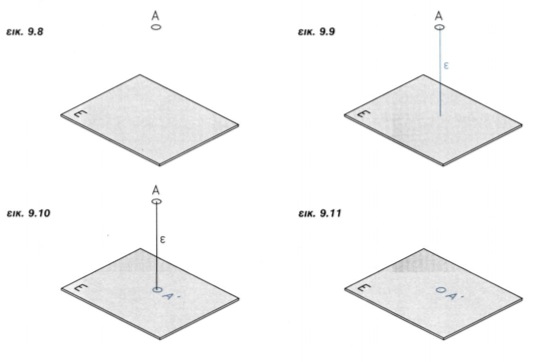
Οι γνωστοί μας γεωγραφικοί χάρτες είναι τοπογραφικά σχέδια και ανήκουν σ'αυτή την κατηγορία, είναι δηλαδή σχέδια ορθών προβολών σε ένα επίπεδο. Στο τεχνικό σχέδιο, χρησιμοποιούμε τοπογραφικά σχέδια για την απόδοση της μορφής του εδάφους γηπέδων και χώρων τους οποίους για διάφορους λόγους θέλουμε να διαμορφώσουμε.
II. Παράσταση σε δύο επίπεδα προβολής
III. Παράσταση σε τρία ή σε περισσότερα επίπεδα προβολής Αν και η παράσταση σε δύο επίπεδα προβολής φαίνεται να είναι αρκετή για μια πλήρη απεικόνιση ενός αντικειμένου, υπάρχουν περιπτώσεις όπου οι δύο προβολές ενός αντικειμένου δεν είναι αρκετές, για να αντιληφθούμε τη μορφή του. Είναι, λοιπόν, πολλές φορές απαραίτητο να καταφύγουμε σε μια τρίτη, τέταρτη κ.ο.κ. προβολή.
9.3.3 Σύστημα ορθών προβολών Ι. Γενικα Κάθε διαδικασία προβολής γενικά προϋποθέτει τρία δεδομένα: 1. Το αντικείμενο προβολής (σχεδίασης) 2. Την επιφάνεια (ή τις επιφάνειες) προβολής και 3. Τον παρατηρητή. Σύστημα ή και μέθοδο ορθών προβολών ονομάζουμε ένα σύνολο επιλογών που προσδιορίζει στοιχεία των τριών αυτών δεδομένων, καθώς και τον τρόπο παρουσίασης του τελικού αποτελέσματος, δηλαδή των όψεων του αντικειμένου επάνω στον πίνακα σχεδίασης. Κάθε σύστημα (ή μέθοδος) ορθών προβολών, ως αποτέλεσμα συμβάσεων, προβλέπεται από τους κανονισμούς τυποποίησης. Τρία είναι τα συστήματα ορθών προβολών που προβλέπονται από τους διεθνείς κανονισμούς (IS0128-1982): το Ευρωπαϊκό, το Αμερικανικό και η μέθοδος του βέλους. Από αυτά, τα δύο πρώτα είναι τα επικρατέστερα, ενώ στη χώρα μας εφαρμόζεται το Ευρωπαϊκό σύστημα. Σε καθένα από τα συστήματα ορθών προβολών προσδιορίζονται: 1. Η θέση του αντικειμένου ως προς το επίπεδο προβολής και ως προς τον παρατη- ρητή. 2. Η δυνατότητα χρησιμοποίησης έξι επιπέδων προβολής, τα οποία, με τη μορφή ενός κύβου, "περικλείουν το αντικείμενο, και στη συνέχεια κατακλίνονται, έτσι ώστε, στην τελική εικόνα που προκύπτει, το 1ο κατακόρυφο (το μετωπικό) επίπεδο να βρίσκεται στο κέντρο του αναπτύγματος. εικ. 9.27 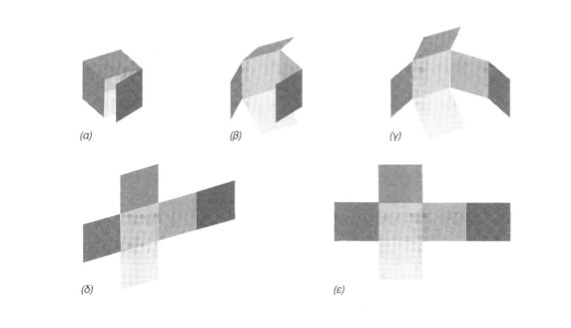
3. Η ονομασία κάθε προβολής, με βάση τη θέση της στο αντίστοιχο επίπεδο προβολής.
Θα πρέπει να επισημάνουμε εδώ ότι οι έδρες του αντικειμένου που προβάλλουμε επιλέγουμε να είναι παράλληλες προς τα επίπεδα προβολής, έτσι ώστε να απλοποιούνται τα σχήματα των προβολών και να διευκολύνεται όλη η διαδικασία. Οι ακμές του αντικειμένου διακρίνονται σε ορατές και μη ορατές από την πλευρά του παρατηρητή. Οι ορατές ακμές παριστάνονται με πλήρη χονδρή γραμμή, ενώ οι μή ορατές με διακεκομένη. Όταν, όμως, συμπίπτουν οι προβολές μιας ορατής ακμής και μιας μη ορατής, τότε στο σχέδιο επικρατεί η πλήρης χονδρή γραμμή.
II. Το Ευρωπαϊκό Σύστημα 1. Η θέση του αντικειμένου βρίσκεται μεταξύ του επιπέδου προβολής και του παρατηρητη. 2. Τα επίπεδα προβολής κατακλίνονται στο 1ο κατακόρυφο επίπεδο, δηλαδή στο επίπεδο Ε2 της πρόοψης (εικ. 9.28). εικ. 9.28 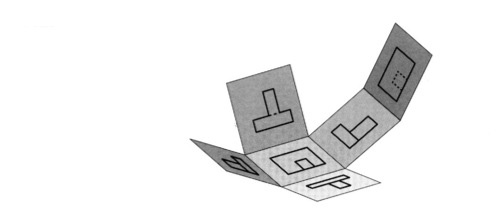
Η ονομασία κάθε προβολής έχει ως εξής (εικ. 9.29). εικ. 9.29 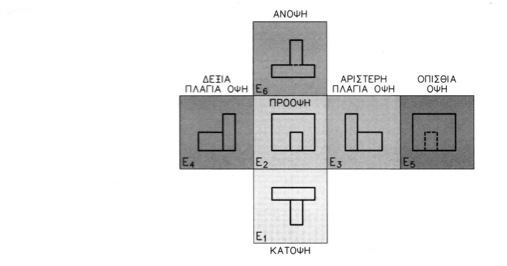
Χρειάζεται εδώ να επισημάνουμε ότι με τον τρόπο που κατακλίνονται τα επίπεδα προβολής, η αριστερή πλάγια όψη σχεδιάζεται δεξιά της πρόοψης, ενώ η δεξιά πλάγια όψη αριστερά της. Προφανώς δεν έχει καμμιά σημασία ποια πλευρά του αντικειμένου επιλέγουμε ως πρόοψη (ή κάτοψη), αφού η μορφή του αντικειμένου, που είναι το ζητούμενο, δεν αλλάζει. Μπορούμε δηλαδή να επιλέξουμε οποιαδήποτε θέση για το αντικείμενο ως προς τα επίπεδα προβολής. Από τη στιγμή όμως που θα οριστεί η μία όψη, αυτόματα έχουν οριστεί και όλες οι υπόλοιπες. Στην πράξη δε χρησιμοποιούμε και τα έξι επίπεδα προβολής συχνά. Συνήθως μας αρκούν τα τρία πρώτα επίπεδα προβολής, αυτά δηλαδή στα οποία προβάλλονται η κάτοψη, η πρόοψη κ α ι η αριστερή πλάγια όψη.
III. Παραδείγματα όψεων απλών στερεών Α. ΟΡΘΟΓΩΝΙΟ ΠΑΡΑΛΛΗΛΕΠΙΠΕΔΟ εικ. 9.30 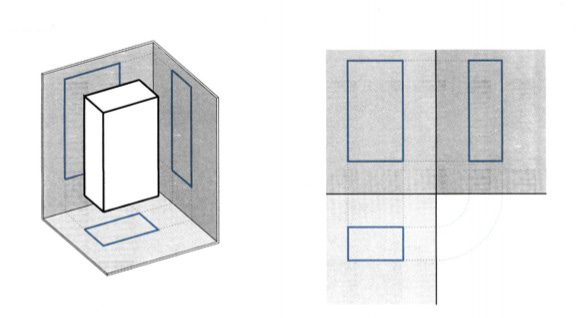
Βήματα σχεδίασης όψεων ορθογώνιου παραλληλεπίπεδου εικ. 9.31 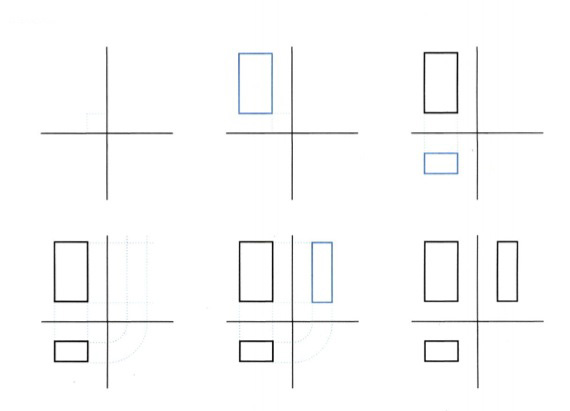
Β. ΣΥΝΘΕΤΟ ΣΤΕΡΕΟ εικ. 9.32 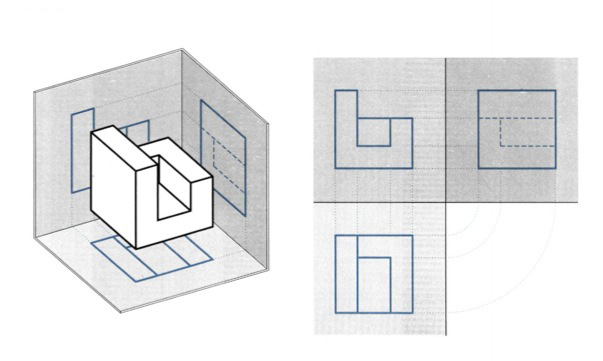
Βήματα σχεδίασης όψεων σύνθετου στερεου εικ. 9.33 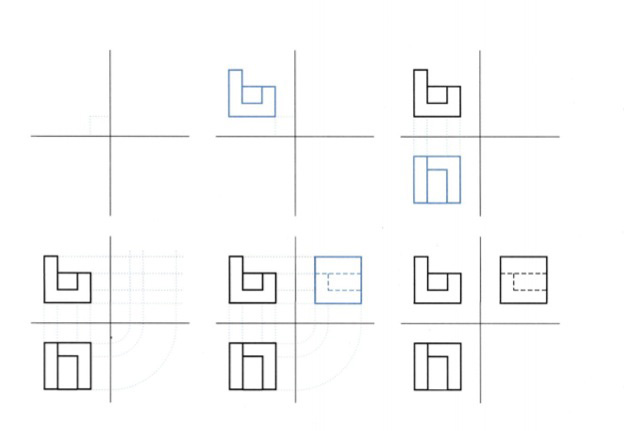
Γ. ΟΡΘΟ ΤΡΙΓΩΝΙΚΟ ΠΡΙΣΜΑ εικ. 9.34 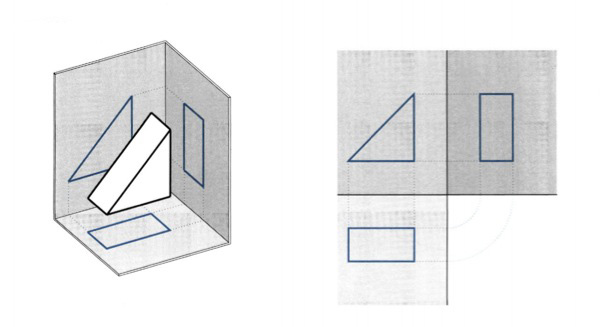
Βήματα σχεδίασης όψεων ορθού τριγωνικού πρίσματος εικ. 9.35 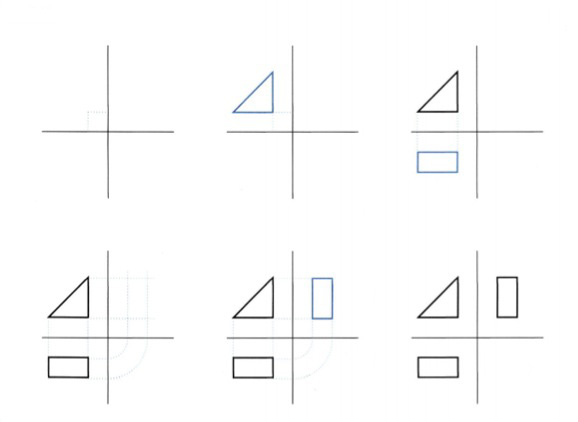
Δ. ΟΡΘΟΣ ΚΥΛΙΝΔΡΟΣ εικ. 9.36 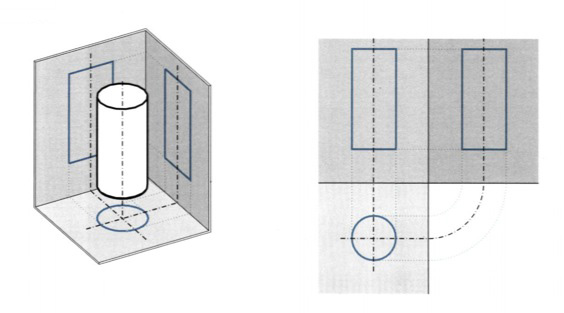
Βήματα σχεδίασης όψεων ορθού κυλίνδρου εικ. 9.37 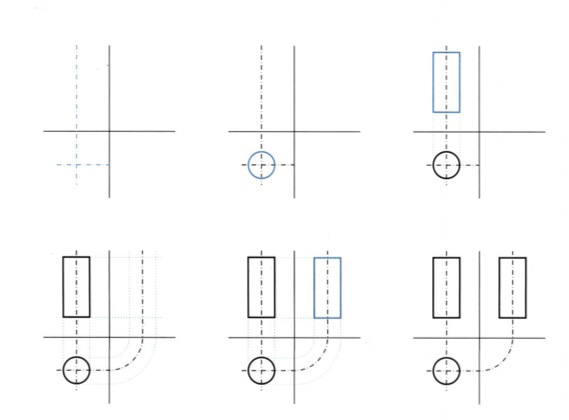
IV. Ασκήσεις Ασκηση 1η Να σχεδιάσετε τις δύο όψεις και στη συνέχεια να συμπληρώσετε την όψη που λείπει, σε κλίμακα 2:1. Οι διαστάσεις των σχεδίων που δίδονται θα στρογγυλοποιούνται σε 0.5 εκ. Θα λάβετε ακόμη υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση δύο ορθογώνιων παραλληλεπίπεδων (εικ. 9.38). εικ. 9.38 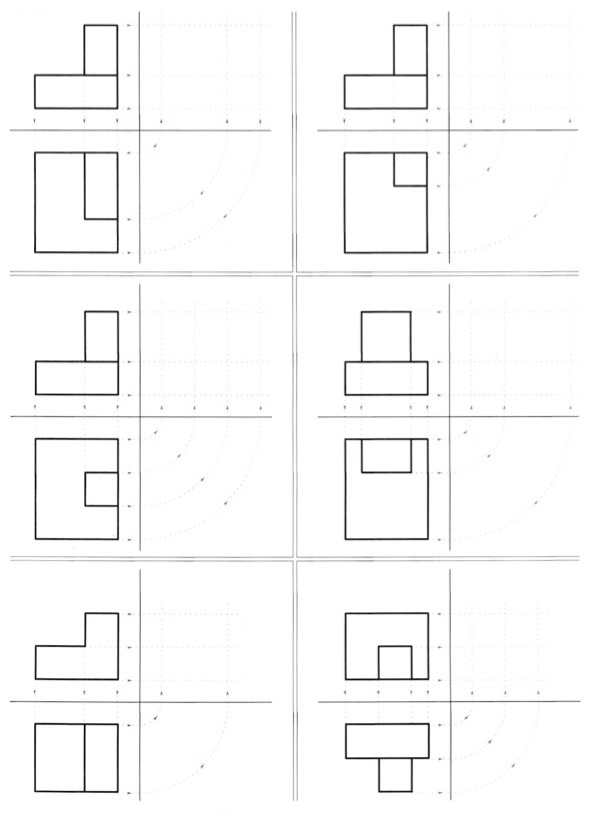
Ασκηση 2η Αν τα σχέδια 1-10 είναι όψεις ενός στερεού, τότε ποια από τα σχέδια 11-20 αντιστοιχούν σ' αυτά ως πλάγιες όψεις (αριστερές) και ταυτόχρονα ποια από τα σχέδια 21-32 αντιστοιχούν σ' α υ τ ά ως κατόψεις; Να σχεδιάσετε τον πίνακα που βρίσκεται στο τέλος της σελίδας και να τον παραδώσετε συμπληρωμένο με τους αντίστοιχους αριθμούς σχεδίων. Θα λάβετε υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση δύο ορθογώνιων παραλληλεπίπεδων (εικ. 9.39). εικ. 9.39 
Ασκηση 3η Αν τα σχέδια 1-10 είναι όψεις ενός στερεού, τότε ποια από τα σχέδια 11-20 αντιστοιχούν σ' αυτά ως πλάγιες όψεις (αριστερές) και ταυτόχρονα ποια από τα σχέδια 21-32 αντιστοιχούν σ' αυτά ως κατόψεις; Να σχεδιάσετε τον πίνακα που βρίσκεται στο τέλος της σελίδας και να τον παραδώσετε συμπληρωμένο με τους αντίστοιχους αριθμούς σχεδίων. Θα λάβετε υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από αφαίρεση ενός ή δύο ορθογώνιων παραλληλεπίπεδων από τρίτο (εικ. 9.40). εικ. 9.40 
Ασκηση 4η Να σχεδιάσετε τις δύο όψεις και στη συνέχεια να συμπληρώσετε την όψη που λείπει, σε κλίμακα 2:1. Οι διαστάσεις των σχεδίων που δίδονται θα στρογγυλοποιούνται σε 0.5 εκ. Θα λάβετε ακόμη υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων (εικ. 9.41). εικ. 9.41 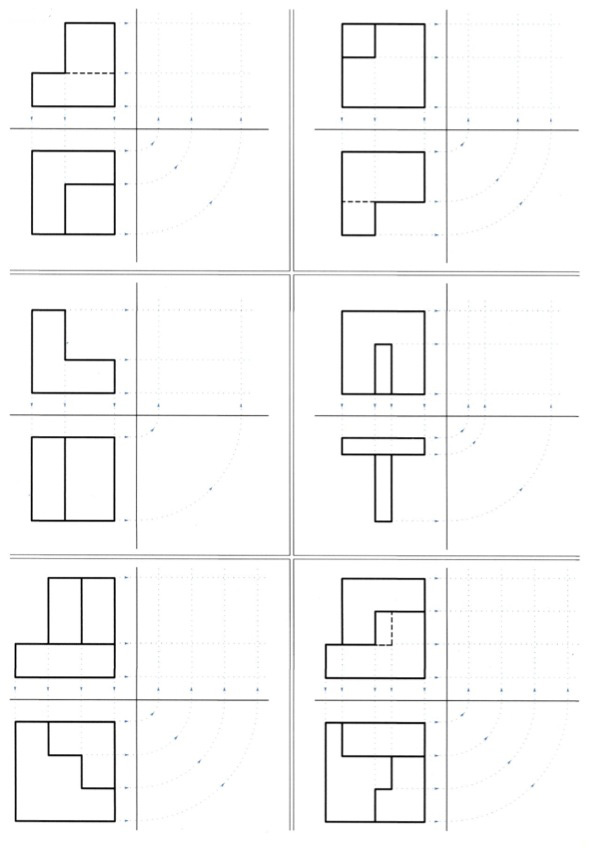
Ασκηση 5η Αν τα σχέδια 1-8 είναι όψεις ενός στερεού, τότε ποια από τα σχέδια 9-16 αντιστοιχούν σ' αυτά ως πλάγιες όψεις (αριστερές) και ταυτόχρονα ποια από τα σχέδια 17-24 αντιστοιχούν σ' αυτά ως κατόψεις: Να σχεδιάσετε τον πίνακα που βρίσκεται στο τέλος της σελίδας και να τον παραδώσετε συμπληρωμένο με τους αντίστοιχους αριθμούς σχεδίων. Θα λάβετε υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων (εικ. 9.42). εικ. 9.42 
Ασκηση 6η Να σχεδιάσετε τις δύο όψεις και στη συνέχεια να συμπληρώσετε την όψη που λείπει, σε κλίμακα 2:1. Οι διαστάσεις των σχεδίων που δίδονται θα στρογγυλοποιούνται σε 0.5 εκ. Θα λάβετε ακόμη υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων και ορθών τριγωνικών πρισμάτων (εικ. 9.43). εικ. 9.43 
Ασκηση 7η Να σχεδιάσετε τις δύο όψεις και στη συνέχεια να συμπληρώσετε την όψη που λείπει, σε κλίμακα 2:1. Οι διαστάσεις των σχεδίων που δίδονται θα στρογγυλοποιούνται σε 0.5 εκ. Θα λάβετε ακόμη υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων και ορθών τριγωνικών πρισμάτων (εικ. 9.44). εικ. 9.44 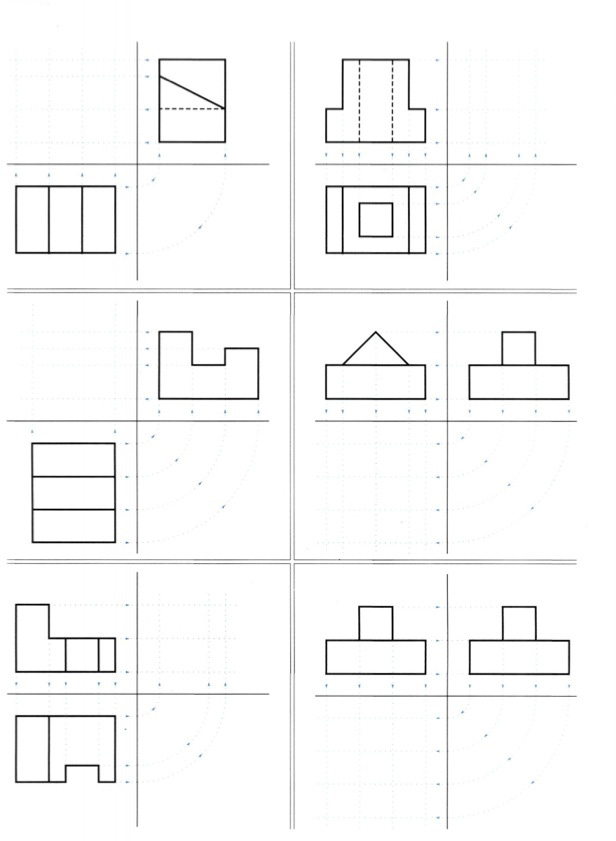
Ασκηση 8η Αν τα σχέδια 1-8 είναι όψεις ενός στερεού, τότε ποια από τα σχέδια 9-16 αντιστοιχούν σ' αυτά ως πλάγιες όψεις (αριστερές) και ταυτόχρονα ποια από τα σχέδια 17-24 αντιστοιχούν σ' αυτά ως κατόψεις; Να σχεδιάσετε τον πίνακα που βρίσκεται στο τέλος της σελίδας και να τον παραδώσετε συμπληρωμένο με τους αντίστοιχους αριθμούς σχεδίων. Θα λάβετε υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων και ορθών τριγωνικών πρισμάτων (εικ. 9.45). εικ. 9.45 
Ασκηση 9η Να σχεδιάσετε τις δύο όψεις και στη συνέχεια να συμπληρώσετε την όψη που λείπει, σε κλίμακα 2:1. Οι διαστάσεις των σχεδίων που δίδονται θα στρογγυλοποιούνται σε 0.5 εκ. Θα λάβετε ακόμη υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων και ορθών κυλίνδρων (εικ. 9.46). εικ. 9.46 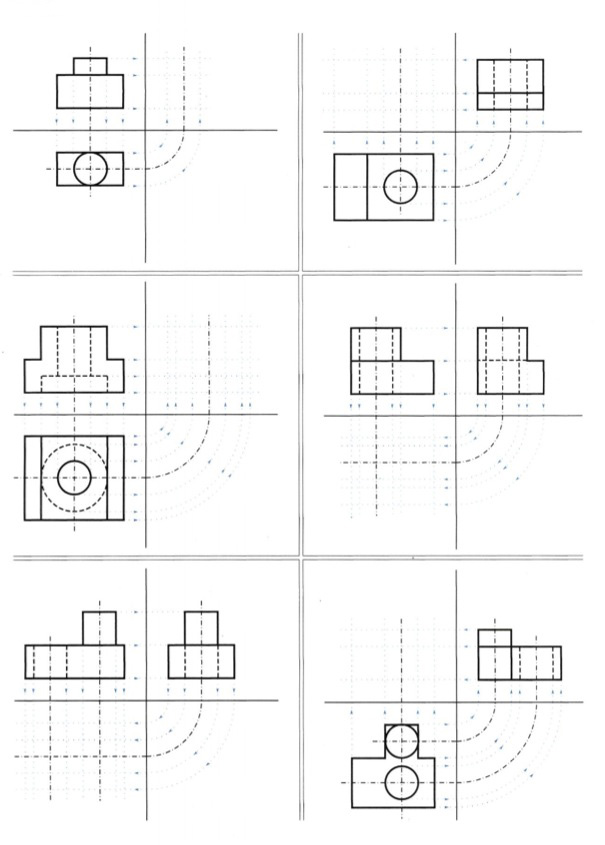
Ασκηση 10η Αν τα σχέδια 1-8 είναι όψεις ενός στερεού, τότε ποια από τα σχέδια 9-16 αντιστοιχούν σ' αυτά ως πλάγιες όψεις (αριστερές) και ταυτόχρονα ποια από τα σχέδια 17-24 αντιστοιχούν σ' αυτά ως κ α τ ό ψ ε ι ς ; Να σχεδιάσετε τον πίνακα που βρίσκεται στο τέλος της σελίδας και να τον παραδώσετε συμπληρωμένο με τους αντίστοιχους αριθμούς σχεδίων. Θα λάβετε υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων και ορθών κυλίνδρων (εικ. 9.47). εικ. 9.47 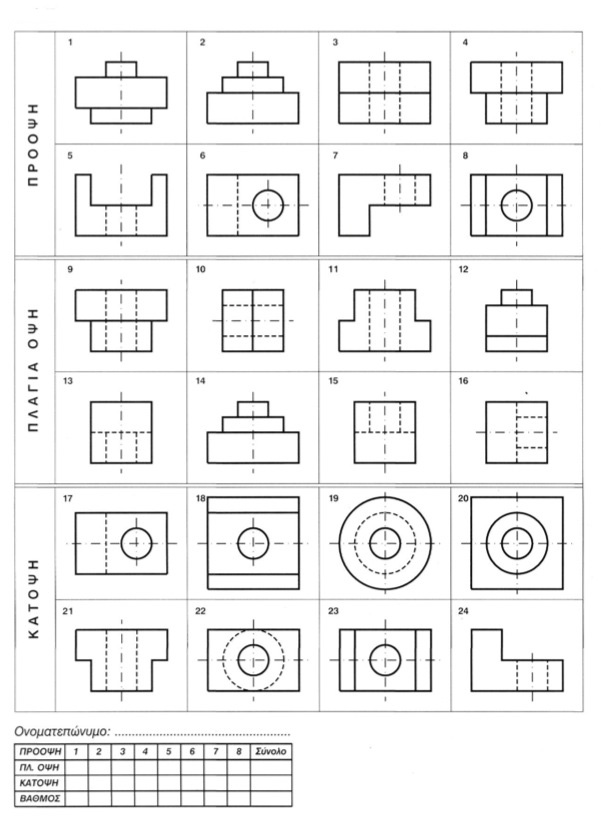
Ασκηση 11η Αν τα σχέδια 1-8 είναι όψεις ενός στερεού, τότε ποια από τα σχέδια 9-16 αντιστοιχούν σ' αυτά ως πλάγιες όψεις (αριστερές) και ταυτόχρονα ποια από τα σχέδια 17-24 αντιστοιχούν σ' αυτά ως κ α τ ό ψ ε ι ς ; Να σχεδιάσετε τον πίνακα που βρίσκεται στο τέλος της σελίδας και να τον παραδώσετε συμπληρωμένο με τους αντίστοιχους αριθμούς σχεδίων. Θα λάβετε υπόψη ότι τα στερεά τα οποία παριστάνονται στις όψεις αυτές προκύπτουν από πρόσθεση ή / και αφαίρεση ορθογώνιων παραλληλεπίπεδων και ορθών κυλίνδρων (εικ. 9.48). εικ. 9.48 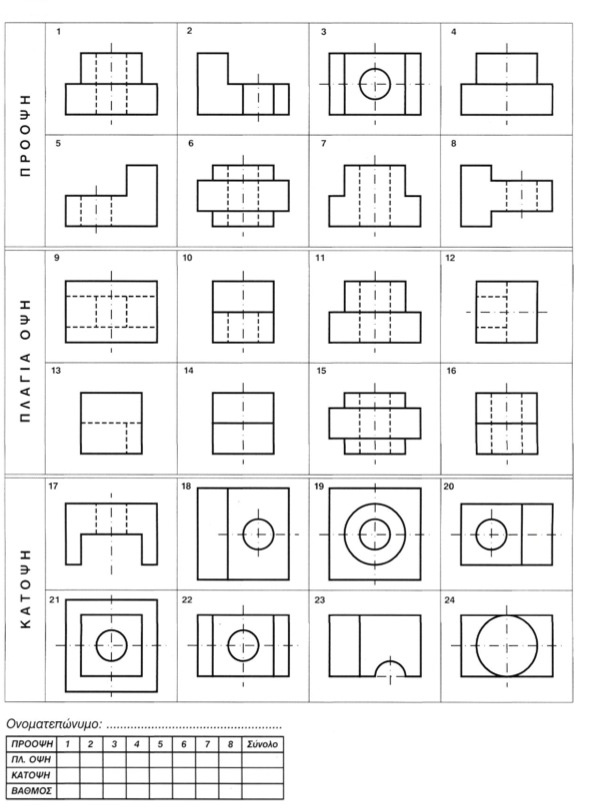
9.3.4 Διαστασιολόγηση όψεων
I. Γενικα Η τοποθέτηση διαστάσεων σε μια σειρά όψεων (πρόοψη, κάτοψη, πλάγια όψη) ακολουθεί σε γενικές γραμμές τους ίδιους κανόνες με τη διαστασιολόγηση απλών επίπεδων σχημάτων που αναπτύχθηκε στο κεφ. 8. Οι διαφορές βρίσκονται σε δύο σημεία: 1. Στις τρεις όψεις υπάρχουν κοινά μεγέθη, (όπως π.χ. τα ύψη στην πρόοψη και στην πλάγια όψη) και πρέπει να αποφύγουμε επαναλήψεις και 2. Τα πραγματικά σχήματα είναι πλέον στερεά, έχουν δηλαδή τρεις διαστάσεις, και με αυτό τον τρόπο πρέπει να τα "αντιλαμβανόμαστε", ώστε να ολοκληρώνουμε τη διαστασιολόγηση τους.
Σημειώνουμε: Έχουμε τη δυνατότητα αλλά και την υποχρέωση να κατανέμουμε τις διαστάσεις σε ό λ ε ς τ ι ς ό ψ ε ι ς , διατηρώντας όμως την ενότητά τους σε επιμέρους μορφές, ώστε να διευκολύνεται η ανάγνωσή τους. Αποφεύγουμε να τοποθετούμε διαστάσεις σε διακεκομένες γραμμές (μη ορατές ακμές). Ειδικά στα αρχιτεκτονικά σχέδια οι διαστάσεις μήκους και πλάτους τοποθετούνται στις κατόψεις (εικ. 10.11), ενώ τα ύψη στα σχέδια τομών και όψεων και μάλιστα με τη μορφή στάθμης που αναφέρεται στο επίπεδο του εδάφους (εικ. 10.24, 10.36).
II. Παραδείγματα διαστασιολόγησης όψεων
Γ. ΔΙΑΣΤΑΣΙΟΛΟΓΗΣΗ ΟΨΕΩΝ ΟΡΘΟΥ ΚΥΛΙΝΔΡΟΥ
εικ. 9.51 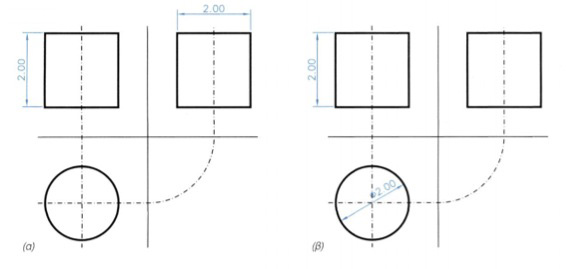
Γ. ΔΙΑΣΤΑΣΙΟΛΟΓΗΣΗ ΟΨΕΩΝ ΑΛΛΩΝ ΣΤΕΡΕΩΝ
εικ. 9.52εικ. 9.53 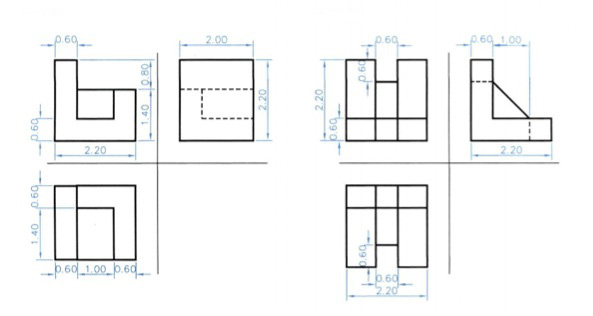
III. Ασκήσεις Να διαστασιολογήσετε σχέδια που έχετε ήδη ολοκληρώσει από τις σελίδες των ασκήσεων της παραγράφου 9.3.3. Θα επιλέξετε από ένα σχέδιο από τις ασκήσεις 1η, 4η, 6η, και 9η.
9.3.5 Τομη
I. Τι είναι η τομη Πολλές φορές χρειάζεται να απεικονίσουμε αντικείμενα που έχουν εσωτερικές κοιλότητες ή πολύπλοκη μορφή η οποία δεν είναι εύκολο να γίνει αντιληπτή από τις όψεις τους. Όταν π.χ. βλέπουμε τις όψεις ενός κτιρίου, δεν μπορούμε να γνωρίζουμε την εσωτερική του διαρρύθμιση ή τη δομή του. Μπορούμε λοιπόν να θεωρήσουμε ότι ένα επίπεδο τέμνει το αντικείμενο σχεδίασης και το χωρίζει σε δύο τμήματα, ώστε, μετά την απομάκρυνση του ενός, να μας αποκαλύπτεται το εσωτερικό του. Το τμήμα που απομένει μπορούμε να το απεικονίσουμε σε ένα σχέδιο ορθής προβολής. Το σχέδιο που προκύπτει από μια τέτοια διαδικασία, το ονομάζουμε τομή. Τομή, λοιπόν, είναι ένα σχέδιο ορθής προβολής ενός αντικειμένου, όπως ακριβώς είναι και μια όψη του. Τομή επίσης ονομάζουμε και τη διαδικασία με την οποία παίρνουμε ένα τέτοιο σχέδιο. Προφανώς, έχουμε τη δυνατότητα να "πραγματοποιήσουμε" περισσότερες από μία τομές σε ένα αντικείμενο και μάλιστα με επίπεδα διαφορετικών διευθύνσεων. Τα σχέδια τομών συνήθως δεν παρουσιάζονται αυτόνομα, αλλά συνδυάζονται με σχέδια όψεων, στα οποία και αναφέρονται και με τα οποία συγκροτούν ενιαία σειρά σχεδίων.
II. Παράσταση της τομής
Α. ΤΟ ΕΠΙΠΕΔΟ ΤΗΣ ΤΟΜΗΣ Το επίπεδο με το οποίο γίνεται τομή το ονομάζουμε επίπεδο τομής (εικ. 9.54). Η θέση του προσδιορίζεται με το ίχνος του (ή τα ίχνη του), δηλαδή την ευθεία (ή τις ευθείες) τομής του, σε ένα (ή περισσότερα) από τα επίπεδα προβολής όπου είναι κάθετο. Συχνά επιλέγουμε επίπεδα τομής κάτακόρυφα και παράλληλα προς το δεύτερο επίπεδο προβολής (εικ. 9.55).
εικ. 9.54εικ. 9.55 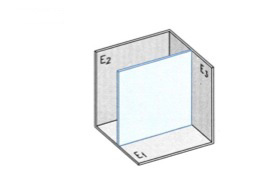 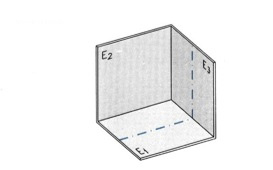
Συγκεκριμένα, η επιφάνεια τομής στο μηχανολογικό σχέδιο καλύπτεται από διαγράμμιση με λεπτές βοηθητικές γραμμές υπό κλίση κλίση 45°. Όταν στο σχέδιο της τομής παρουσιάζονται δύο διαφορετικά μέρη σε επαφή, οι τεμνόμενες επιφάνειες έχουν διαγραμμίσεις με κάθετη μεταξύ τους διεύθυνση και πάλι με κλίση 45° ως προς την οριζόντια διεύθυνση. Στο αρχιτεκτονικό σχέδιο, η τεμνόμενη επιφάνεια περικλείεται από χοντρές πλήρεις γραμμές με ή χωρίς πρόσθετη διαγράμμιση ή άλλη τονική διαφοροποίηση (εικ. 10.11, 10.24). Υπάρχει ακόμη η δυνατότητα να διαφοροποιούνται οι επιφάνειες τομής με συμβολισμό των υλικών τους. Εδώ οι τεμνόμενες επιφάνειες των διαφορετικών δομικών στοιχείων μπορούν να εμφανίζονται με ενιαία διαγράμμιση και ακόμη και με ενιαίο περίγραμμα.
III. Παραδείγματα τομών
Α. ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στα σχέδια τομών δεν παριστάνονται ακμές του αντικειμένου που δεν είναι ορατές, δηλαδή δεν υπάρχουν διακεκομμένες γραμμές. 2. Κατά τη διαστασιολόγηση σχεδίων τομών αποφεύγουμε τη αναγραφή διαστάσεων μέσα στην τεμνόμενη επιφάνεια. Άν δεν είναι αυτό δυνατό, τότε η διαγράμμιση πρέπει να διακόπτεται στο σημείο που γράφεται η αριθμητική τιμή της διάστασης,
Β. ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΧΕΔΙΩΝ ΤΟΜΩΝ
εικ. 9.58 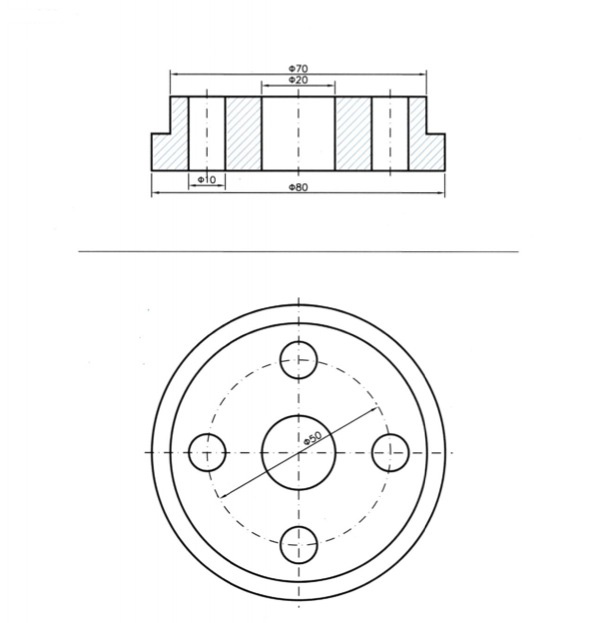
εικ. 9.59 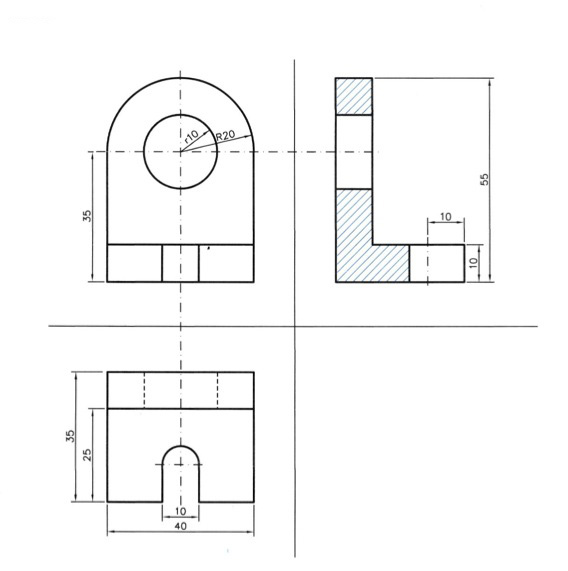
IV. Άλλα είδη τομών
Η λέξη ημιτομή σημαίνει μισή τομή. Ένα σχέδιο ημιτομής είναι δηλαδή σχέδιο τομής κατά το ήμισυ, ενώ το υπόλοιπο τμήμα του σχεδίου (δηλαδή της ορθής προβολής) είναι όψη (κατά το ήμισυ) του αντικειμένου. Αυτό γίνεται για λόγους διευκόλυνσης, με την προϋπόθεση όμως ότι το τμήμα που παρουσιάζεται σε τομή είναι το ίδιο με εκείνο το οποίο παρουσιάζεται σε όψη. Μεταξύ των δύο τμημάτων του σχεδίου, όψης και τομής, παρεμβάλλεται λεπτή αξονική γραμμή. Εκτός από την ημιτομή υπάρχουν και άλλα δύο είδη τομών, η μερική τομή και η τοπική τομή. Με τη μερική τομή αποτέμνεται ένα μικρό μέρος του αντικειμένου και απομένει για σχεδίαση το υπόλοιπο, ενώ με την τοπική τομή, η οποία είναι πλήρης τομή, απεικονίζεται ένα τμήμα ενός συνόλου (π.χ. με επάλληλες τοπικές οριζόντιες τομές απεικονίζεται το πόδι ενός τραπεζιού).
ΠΑΡΑΔΕΙΓΜΑ ΗΜΙΤΟΜΗΣ
εικ. 9.60 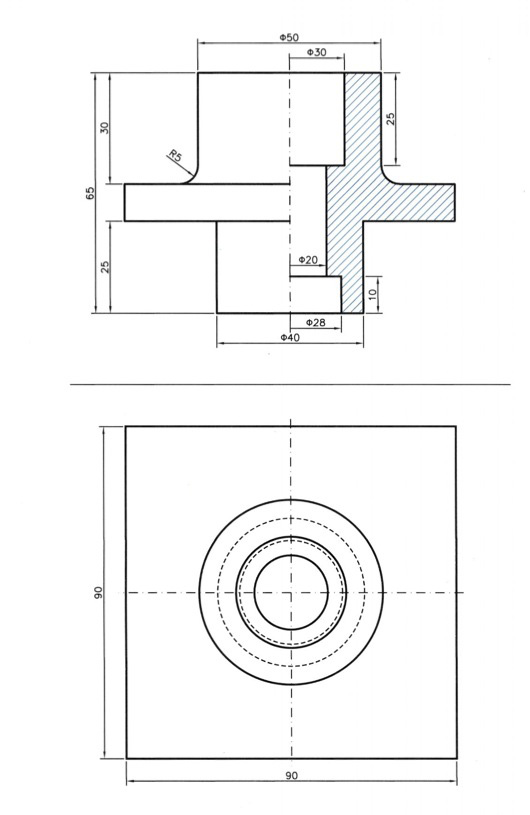
9.3.6 Αξονομετρικές προβολές
I. Γενικα Αξονομετρική προβολή ή αξονομετρικό σχέδιο ενός αντικειμένου ονομάζουμε μια παράλληλη προβολή του, ορθή ή πλάγια, σε ένα μόνο επίπεδο προβολής. Σε ένα αξονομετρικό σχέδιο πρέπει να εμφανίζονται όλες οι βασικές έδρες ενός αντικειμένου. Στην ορθή προβολή, οι βασικές έδρες ενός αντικειμένου πρέπει να έχουν κλίση, ενώ στην πλάγια προβολή, μπορούν να είναι και παράλληλες ως προς το επίπεδο προβολής. Βασική επιδίωξη ενός αξονομετρικού σχεδίου είναι να αποδίδονται και οι τρεις διαστάσεις του χώρου, παράλληλα με τη διατήρηση του τεχνικού του χαρακτήρα. Υπάρχουν, όπως αντιλαμβανόμαστε, δυνατότητες παρουσίασης άπειρων αξονομετρικών προβολών. Στην πράξη όμως χρησιμοποιούμε έναν πολύ περιορισμένο αριθμό από αυτές με κριτήρια τις ανάγκες τυποποίησης αλλά και την ευκολία σχεδίασης με τη χρήση απλών οργάνων (τριγώνων και διαβήτη). Θεωρείται αυτονόητο ότι οι προβολές που έχουν επικρατήσει αποδίδουν καλύτερα την πραγματική μορφή του αντικειμένου.
II. Είδη αξονομετρικών προβολών Όπως προαναφέραμε, σε μια αξονομετρική προβολή παρουσιάζονται οι τρεις βασικές διαστάσεις. Πα παράδειγμα, το σχέδιο ενός κύβου θα περιλαμβάνει όλες τις ακμές και όλες τις έδρες του. Από τη Στερεομετρία γνωρίζουμε ότι οι παράλληλες ακμές του κύβου θα είναι και στο σχέδιο παράλληλες (ανά τέσσερις). Στο σχέδιο, λοιπόν, θα έχουμε τρεις χαρακτηριστικές διευθύνσεις, μήκους, πλάτους, ύψους, από τις οποίες και θα προσδιορίζονται οι μορφές των εδρών του. Τις διευθύνσεις αυτές τις ορίζουμε με τρεις άξονες, τους χ, ψ, ζ αντίστοιχα. Ο άξονας ζ του ύψους σχεδιάζεται πάντοτε κατακόρυφος. Η κλίση κάθε άξονα, εξαρτάται προφανώς από την κλίση της κάθε έδρας του κύβου προς το επίπεδο προβολής. Αυτό πρακτικά σημαίνει ότι μεγέθη διαφορετικών διευθύνσεων, τα οποία στην πραγματικότητα είναι ίσα, στο σχέδιο είναι διαφορετικά. Άρα, πρέπει να υπάρχουν κλίμακες συσχετισμού μεταξύ των τριών αξόνων σε κάθε αξονομετρική προβολή. Οι κλίμακες αυτές προφανώς εφαρμόζονται ανεξάρτητα από την κλίμακα σχεδίασης που κάθε φορά ισχύει.
Με βάση ακριβώς τις κλίμακες αυτές οι αξονομετρικές προβολές διακρίνονται σε τρία είδη: α. Τις μονομετρικές, όταν υπάρχει μια ενιαία κλίμακα συσχετισμού για όλα τα ζεύγη αξόνων (ανά δύο) β. τις διμετρικές, όταν υπάρχουν δύο κλίμακες (μια κοινή για τους δύο από τους άξονες και άλλη για τον τρίτο) και γ. τις τριμετρικές, όταν για κάθε ζεύγος αξόνων η κλίμακα συσχετισμού είναι διαφορετική. Από τα είδη αυτά χρησιμοποιούμε κυρίως δύο μονομετρικές και τρεις έως τέσσερις διμετρικές, από τις οποίες μία μονομετρική και μία διμετρική είναι τυποποιημένες. Κάθε αξονομετρική προβολή ορίζεται λοιπόν από τις διευθύνσεις των αξόνων της χ, ψ, και ζ και από τις κλίμακες συσχετισμού τους. Οι διευθύνσεις των αξόνων προσδιορίζονται με τη γωνία κλίσης τους ως προς την οριζόντια διεύθυνση με κατακόρυφο πάντοτε τον άξονα ζ του ύψους.
III. Πορεία εργασίας
Α. ΓΕΝΙΚΑ Η πορεία εργασίας που ακολουθεί αναφέρεται σε ένα ορθογώνιο παραλληλεπίπεδο. Κάθε άλλη περίπτωση στερεού είναι δυνατό να αναχθεί σε μια διαδοχική εφαρμογή αυτής της απλής περίπτωσης, αρκεί να έχουμε αντιληφθεί σωστά την πραγματική μορφή του αντικειμένου στο χώρο. Προς αυτή την κατεύθυνση διευκολύνει να προσπαθούμε να συλλάβουμε τα συνθετότερα στερεά ως αποτέλεσμα μιας προσθαφαίρεσης απλών όγκων, αρχίζοντας από το περίγραμμα του μεγαλύτερου όγκου του συνόλου σχεδιάζουμε διαδοχικά τους μικρότερους όγκους, οι οποίοι αφαιρούνται ή προστίθενται έως ότου καταλήξουμε στην τελική μορφή.
Β. ΒΗΜΑΤΑ ΣΧΕΔΙΑΣΗΣ ΑΞΟΝΟΜΕΤΡΙΚΟΥ ΟΡΘΟΓΩΝΙΟΥ ΠΑΡΑΛΛΗΛΕΠΙΠΕΔΟΥ
εικ. 9.67 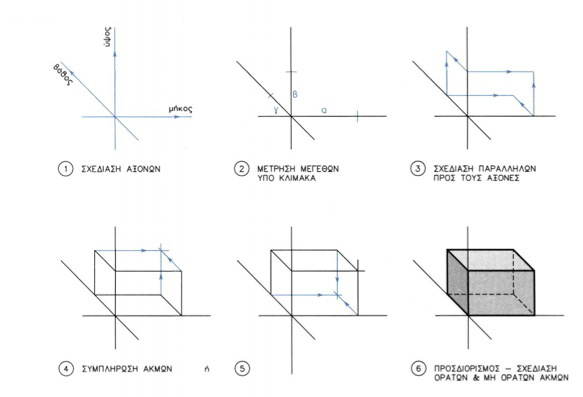
IV. Παρατηρήσεις Στο αξονομετρικό σχέδιο, έχουμε τη δυνατότητα μέτρησης μεγεθών και σχεδίασης υπό κλίμακα. Αυτό όμως ισχύει μόνο για τα ευθύγραμμα τμήματα που είναι παράλληλα προς έναν από τους άξονες. Δεν έχουμε αντίθετα τη δυνατότητα να μετρήσουμε γωνίες παρά μόνο σε ορισμένες περιπτώσεις (οπως στις έδρες που διατηρούν τη μορφή τους, στις προβολές Cavallier). Όταν χρειάζεται να ορίσουμε τη θέση ενός σημείου στο χώρο του αντικειμένου, τότε βρίσκουμε τις αποστάσεις του (τις συντεταγμένες) από τις έδρες του αντικειμένου, μετρώντας πάντοτε παράλληλα με τους άξονες. Με ανάλογο τρόπο από δύο σημεία ορίζουμε μια ευθεία, ένα σχήμα κ.ο.κ.
IV. Ασκήσεις Με δεδομένα τα σχέδια των όψεων των στερεών τα οποία έχετε ήδη ολοκληρώσει στα πλαίσα των προηγούμενων ασκήσεων της παραγράφου 9.3.3: 1. Να επιλέξετε για σχεδίαση δύο στερεά, το ένα από τα οποία να περιλαμβάνει και πρισματική επιφάνεια. 2. Να καταγράψετε τα βήματα σχεδίασης σύμφωνα με αυτά. 3. Να σχεδιάσετε καθένα από τα δύο στερεά σε μια αξονομετρική προβολή, μια μονομετρική και μιαδιμετρική, υπό κλίμακα 2/1.
9.3.7 Ασκήσεις επανάληψης Δίδονται αξονομετρικές προβολές διάφορων αντικειμένων με τις απαραίτητες διαστάσεις : α) σε χιλιοστά, για τα σχέδια των εικόνων 9.68 και 9.69, β) σε εκατοστά, για το σχέδιο της εικόνας 9.70 και γ) σε μέτρα, για τα σχέδια των εικόνων 9.71 και 9.72. Επί πλέον δίδεται η πρόοψη για καθένα από τα αντικείμενα των εικόνων 9.68, 9.69 και 9.70. Αφού επιλέξετε κλίμακα σχεδίασης, να σχεδιάσετε : 1. Τα αντικείμενα των εικόνων 9.68 και 9.69 σε διμετρική αξονομετρική προβολή, με γωνίες αξόνων a1=0° και α2=45° και κλίμακα συσχετισμού χ:ψ:ζ=2:2:1 2. Τα αντικείμενα των εικόνων 9.68, 9.69, 9.70 σε σειρά σχεδίων, που θα περιλαμβάνει κάτοψη, (αριστερή) πλάγια όψη και τομή ή ημιτομή αντί της πρόοψης, η οποία δίδεται, και 3. Τα αντικείμενα των εικόνων 9.71 και 9.72 σε σειρά σχεδίων, που θα περιλαμβάνει πρόοψη, κάτοψη και (αριστερή) πλάγια όψη. Σε όλα τα σχέδια θα αναγράφονται οι τίτλοι (π.χ. πρόοψη, κάτοψη κτλ.) και η κλίμακα σχεδίασης.
εικ. 9.68 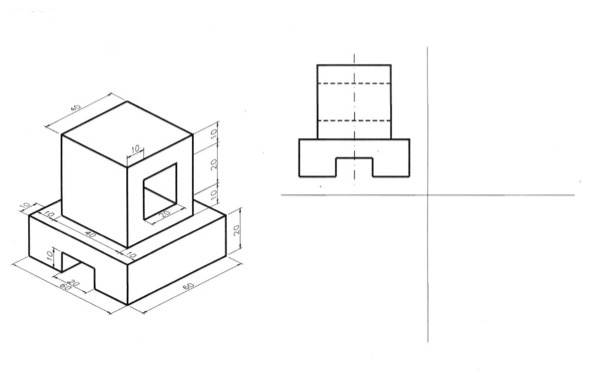
εικ. 9.69 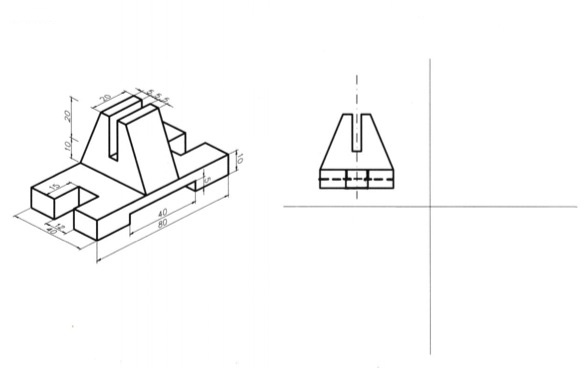
εικ. 9.70 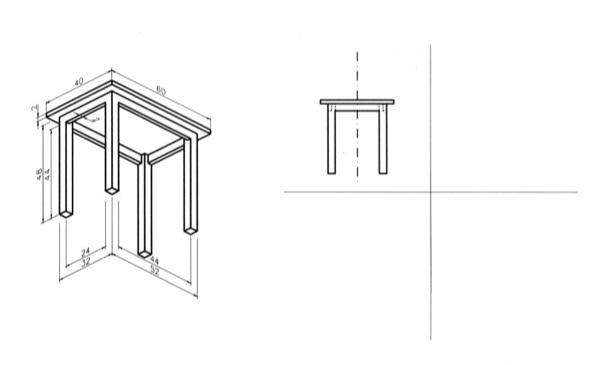
εικ. 9.71 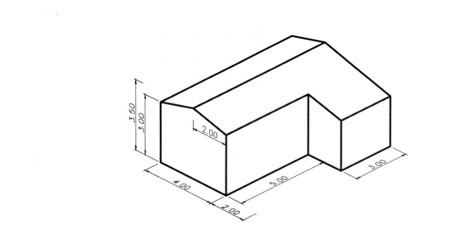
εικ. 9.72 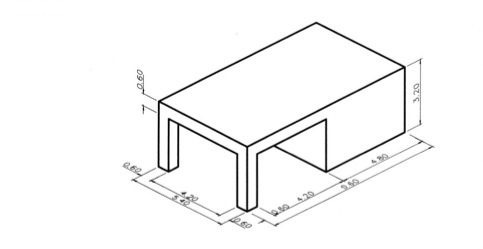
|
||||||||||||||||||||||||||||||||||||||||||||||||||