ΠΡΟΒΟΛΕΣ
9.2 Στοιχεία Παραστατικής Γεωμετρίας 9.2.1 Γενικα Οι αναφορές που ακολουθούν έχουν σκοπό είτε να επαναφέρουν στη μνήμη μας είτε να μας γνωρίσουν έννοιες και μεθόδους της Παραστατικής Γεωμετρίας τις οποίες χρησιμοποιούμε, για να παραστήσουμε τη μορφή ενός αντικειμένου σε σχέδιο, αλλά και, αντίστροφα, για να μπορούμε από το σχέδιο να κατανοήσουμε στη μορφή του αντικειμένου. Η παράσταση ενός αντικειμένου είναι μια εικόνα του επάνω σ'ένα χαρτί' μια εικόνα που σχεδόν πάντοτε έχει μέγεθος διαφορετικό από το φυσικό μέγεθος του αντικειμένου. Πα να είναι λοιπόν εφικτή η παράσταση ενός αντικειμένου, πρέπει να γίνει μια σμίκρυνση ή μεγέθυνση, που είναι ανεξάρτητη από οποιεσδήποτε άλλες γεωμετρικές πράξεις. Η περιγραφή των εννοιών και των μεθόδων, που ακολουθεί, περιλαμβάνει την αντιμετώπιση των προβλημάτων παράστασης ενός σημείου. Η δυνατότητα παράστασης ευθειών, σχημάτων, στερεών και άλλων αντικειμένων με σύνθετη μορφή στηρίζεται στο γεγονός ότι κάθε εικόνα συγκροτείται από χαρακτηριστικά σημεία, τα οποία μπορούν να προσδιοριστούν σύμφωνα με το προηγούμενο πρότυπο. Η επίλυση όλων των προβλημάτων παράστασης ενός αντικειμένου στηρίζεται στην επίλυση των προβλημάτων παράστασης ενός τυχαίου σημείου του χώρου.
9.2.2 Βασικές έννοιες
Ι. Η προβολη Προβολή ενός σημείου Α' του χώρου σε ένα επίπεδο Ε ονομάζουμε το σημείο Α', που είναι η τομή με το επίπεδο Ε μιας ευθείας ε που περνάει από το σημείο Α. Το επίπεδο Ε ονομάζεται επίπεδο προβολής και η ευθεία ε ευθεία προβολής (εικ. 9.1, 9.3, 9.5). Η προβολή α' μιας ευθείας α ορίζεται από τις αντίστοιχες προβολές δύο χαρακτηριστικών σημείων της (εικ. 9.2, 9.4, 9.6). Με ανάλογο ακριβώς τρόπο, δηλαδή από τις προβολές χαρακτηριστικών σημείων τους, ορίζονται και οι προβολές ενός επίπεδου σχήματος, ενός στερεού κ.ο.κ. Ανάλογα με τον τρόπο με τον οποίο ορίζεται η ευθεία προβολής διακρίνουμε δύο είδη προβολών, τις παράλληλες και τις κεντρικές προβολές.
Α. ΠΑΡΑΛΛΗΛΕΣ ΠΡΟΒΟΛΕΣ Παράλληλη προβολή έχουμε όταν κάθε ευθεία προβολής είναι παράλληλη προς μια άλλη ευθεία δ, η οποία χρησιμοποιείται ως οδηγός όλων των ευθειών προβολής. Η ευθεία δ μπορεί να έχει τυχαία κλίση ως προς το επίπεδο προβολής Ε και τότε έχουμε μια πλάγια προβολή (εικ. 9.1, 9.2).
εικ. 9.1εικ. 9.2 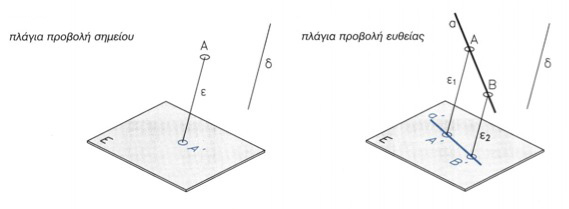
Όταν η ευθεία δ είναι κάθετη προς το επίπεδο προβολής Ε, τότε έχουμε την ορθή προβολή (εικ. 9.3, 9.4).
εικ. 9.3εικ. 9.4 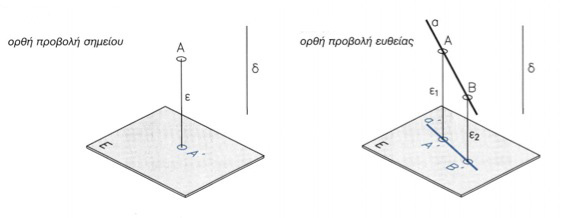
Β. ΚΕΝΤΡΙΚΗ ΠΡΟΒΟΛΗ Κεντρική προβολή έχουμε όταν κάθε ευθεία προβολής διέρχεται από ένα σημείο Ο, το οποίο ονομάζουμε κέντρο προβολής (εικ. 9.5, 9.6):
εικ. 9.5εικ. 9.6 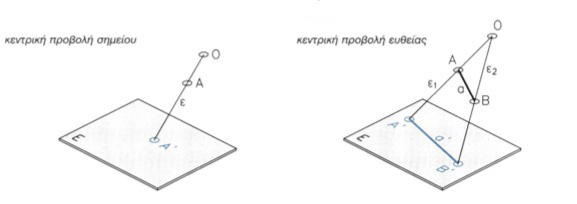
II. Η κατάκλιση Κατάκλιση ενός επιπέδου Ε2 επάνω σ'ένα άλλο επίπεδο Ε1 είναι η περιστροφή του Ε2, με άξονα περιστροφής την ευθεία τομής τους, έως ότου συμπέσει με το Ε1. Κατά την κατάκλιση προφανώς περιστρέφεται και κάθε στοιχείο που περιλαμβάνει το περιστρεφόμενο επίπεδο Ε2 (εικ, 9.7).
εικ. 9.7 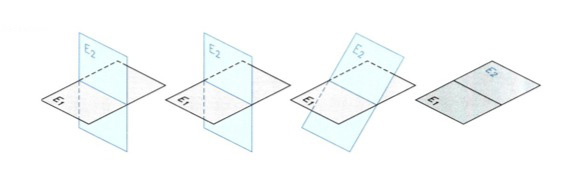
Η ακριβώς αντίστροφη περιστροφή, ώστε το επίπεδο να επανέλθει στην προηγούμενη θέση του, ονομάζεται ανάκλιση.
|