8.2 Τρόπος διαστασιολόγησης

8.2.1 Μορφή διαστάσεων

Γενικά, η μορφή των διαστάσεων στο σχέδιο αποτελεί αντικείμενο κανονισμών ακολουθεί τις κατά περίπτωση ιδιαιτερότητες που απαιτεί το είδος του σχεδίου στο οποίο αναφέρονται.

Κάθε διάσταση αποτελείται από:

• τη γραμμή ή τις γραμμές διάστασης
• τις βοηθητικές γραμμές διάστασης
• τα σύμβολα αρχής - τέλους και
• την αριθμητική τιμή.

Γραμμή (γραμμές) διάστασης Οι γραμμές της διάστασης σχεδιάζονται πάντοτε παράλληλες προς το στοιχείο (ευθ. τμήμα) στο οποίο αναφέρεται η διάσταση, συνήθως σε απόσταση 8-10 χιλ. από αυτό και, ανάλογα με το είδος των συμβόλων αρχής - τέλους, μπορούν να προεκτείνονται λίγο μετά τις βοηθητικές γραμμές διάστασης (εικ. 8.1).

εικ. 8.1

Βοηθητικές γραμμές διάστασης Οι βοηθητικές γραμμές διάστασης ξεκινούν από τα άκρα (ή συνηθέστερα σε μικρή απόσταση από αυτά) του τμήματος στο οποίο αναφέρεται η διάσταση και εκτείνονται λίγο μετά τη γραμμή της διάστασης (εικ. 8.2). Οι βοηθητικές γραμμές διάστασης είναι συνήθως κάθετες στο τμήμα που αναφέρεται η διάσταση αλλά και πλάγιες, όταν απαιτείται. Κατά τη διαστασιολόγηση αποφεύγουμε να διασταυρώνονται οι γραμμές αυτές.

εικ. 8.2

Σύμβολα αρχής - τέλους Τα σύμβολα αρχής - τέλους τοποθετούνται στα σημεία επαφής των βοηθητικών γραμμών διάστασης και της γραμμής (γραμμών) διάστασης (εικ. 8.3). Η γεωμετρική μορφή τους καθορίζεται από τις συμβάσεις (κανονισμούς). Από τα σύμβολα που ισχύουν στη χώρα μας, τα βέλη χρησιμοποιούνται κυρίως στο μηχανολογικό σχέδιο (εικ. 8.3 α,δ), ενώ στα αρχιτεκτονικά σχέδια εφαρμόζονται οι υπόλοιπες μορφές συμβόλων (εικ. 8.3 β,γ,ε,στ).

εικ. 8.3

Αριθμητική τιμη Η αριθμητική τιμή τοποθετείται παράλληλα με τη γραμμή διάστασης στο μέσον (κατά προσέγγιση) του μήκους της και κατά περίπτωση πάνω (εικ. 8.4 α, δ) ή κάτω από αυτή. Από τα σύμβολα που ισχύουν στη χώρα μας, τα βέλη χρησιμοποιούνται κυρίως στο μηχανολογικό σχέδιο (εικ. 8.3 α,δ), ενώ στα αρχιτεκτονικά σχέδια εφαρμόζονται οι υπόλοιπες μορφές συμβόλων (εικ. 8.3 β,γ,ε,στ).

εικ. 8.4

Η τιμή της διάστασης αναφέρεται υποχρεωτικά σε μέτρα, με την προσθήκη δύο δεκαδικών ψηφίων (έστω και μηδενικών) χωρίς όμως την αναγραφή ένδειξης των μονάδων. Ειδικά για τις μεταλλικές κατασκευές, και πολλές φορές και για τις ξύλινες, η τιμή αναφέρεται σε χιλιοστά και πάλι χωρίς αναγραφή μονάδων.

Στις αγγλοσαξωνικές χώρες οι διαστάσεις αναφέρονται σε ίντσες (π.χ. 2"), πόδια (ft) ή κλάσματα της ίντσας (π.χ. 3/4").

8.2.2 Τοποθέτηση διαστάσεων

Γενικά, σε κάθε σχήμα θα μπορούσαμε να διακρίνουμε τρία είδη διαστάσεων:

α. τις διαστάσεις του εξωτερικού περιγράμματος του συνόλου (εικ. 8.5).	εικ. 8.5
β. τις διαστάσεις των περιγραμμάτων των επιμέρους μορφών (εικ. 8.6).	εικ. 8.6
γ. τις διαστάσεις που προσδιορίζουν τη θέση των επι μέρους ως προς το σύνολο (εικ. 8.7).	εικ. 8.7

Η διαστασιολόγηση διέπεται από ορισμένες αρχές, τις οποίες καλό είναι να λαμβάνουμε υπόψη σε κάθε περίπτωση. Συγκεκριμένα:

1. Οι διαστάσεις να καλύπτουν όλα τα στοιχεία της μορφής χωρίς επαναλήψεις.

2. Οι διαστάσεις να είναι ευανάγνωστες και να διακρίνεται το στοιχείο στο οποίο αναφέ- ρονται.

8.2.3 Παραδείγματα διαστασιολόγησης

Τα παραδείγματα διαστασιολόγησης απλών επίπεδων σχημάτων που ακολουθούν θα μας βοηθήσουν στη διαστασιολόγηση άλλων, συνθετότερων μορφών.

Διαστασιολόγηση ορθογωνίου (εικ. 8.8).

εικ. 8.8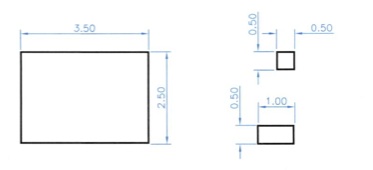

Διαστασιολογηση κύκλου (εικ. 8.9).

α. με την ακτίνα και

β. με τη διάμετρο

εικ. 8.9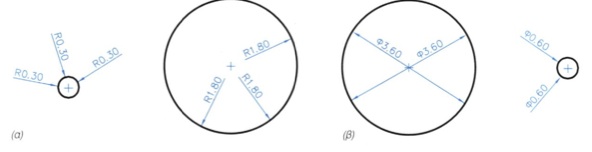

Η διαστασιολόγηση ενός τόξου δε διαφέρει σε τίποτε από τη διαστασιολόγηση του αντίστοιχου κύκλου.

Διαστασιολόγηση γωνίας (εικ. 8.10).

εικ. 8.10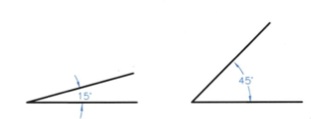

Κατά τη διαστασιολόγηση καταβάλλουμε προσπάθεια να μη διασταυρώνονται οι γραμμές των διαστάσεων (εικ. 8.11):

εικ. 8.11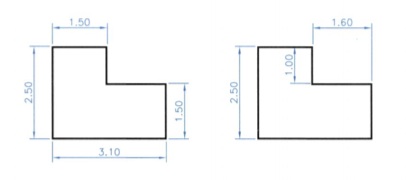

Διαστασιολόγηση με αναφορά σε δύο άξονες (εικ. 8.12).

εικ. 8.12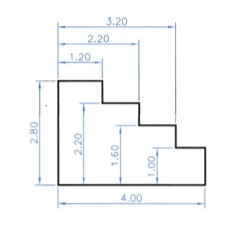

Διαστασιολόγηση με χρήση αξονικής γραμμής, η οποία δηλώνει συμμετρία ως προς άξονα, με αποτέλεσμα να μειώνεται ο αριθμός των απαιτούμενων διαστάσεων (εικ. 8.13).

εικ. 8.13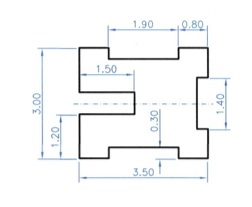