6.4 Πολύγωνα

Πολύγωνο ονομάζεται κάθε κλειστά γεωμετρικό σχήμα που αποτελείται από διαδοχικά ευθύγραμμα τμήματα (εικ. 6.14).

εικ. 6.14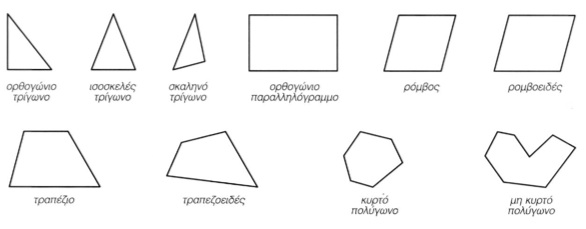

Όταν όλες οι πλευρές και οι εσωτερικές γωνίες του πολύγωνου είναι ίσες, τότε λέγεται κανονικό πολύγωνο (εικ. 6.15).

εικ. 6.15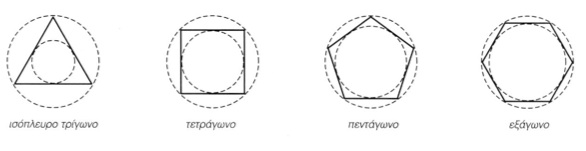

Κάθε κανονικό πολύγωνο μπορεί να εγγραφεί ή να περιγραφεί σε κύκλο.

Κανονικά πολύγωνα με πολλαπλάσιο αριθμό πλευρών από αυτά που θα εξετάσουμε προκύπτουν, αν διχοτομήσουμε τις εσωτερικές γωνίες τους. Επειδή οι διχοτόμοι των γωνιών έχουν την ιδιότητα να διχοτομούν και τα αντίστοιχα τόξα, ο κύκλος χωρίζεται σε διπλάσιο αριθμό ίσων τμημάτων. Για παράδειγμα, από το τετράγωνο μπορεί να προκύψει οκτάγωνο, δεκαεξάγωνο, τριανταδυάγωνο κ.ο.κ. (εικ. 6.16).

6.4.1 Κατασκευή ισόπλευρου τριγώνου όταν είναι γνωστή η πλευρά του (εικ. 6.17)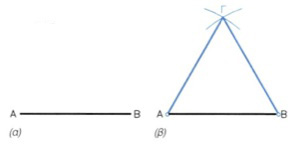

εικ. 6.17

α. Έστω ευθύγραμμο τμήμα ΑΒ ίσο με την πλευρά του ζητούμενου τριγώνου,

β. Με κέντρα τα Α και Β και ακτίνα R ίση με ΑΒ γράφω τόξα που τέμνονται στο Γ. Το τρίγωνο ΑΒΓ είναι ισόπλευρο

εικ. 6.18

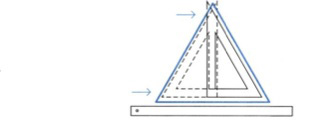
Πρακτικά, η κατασκευή του ισόπλευρου τριγώνου γίνεται με τη χρήση του τριγώνου 60°, όπως φαίνεται στο σχήμα, (εικ. 6.18).

Για την κατασκευή οποιουδήποτε τριγώνου, όταν είναι γνωστές οι πλευρές του (α, β, γ), ορίζω ευθύγραμμο τμήμα ίσο με τη μία πλευρά, και με κέντρα τα άκρα του και αντίστοιχες ακτίνες ίσες με τις δύο άλλες πλευρές γράφω τόξα που τέμνονται στο σημείο Γ. Το τρίγωνο ΑΒΓ είναι το ζητούμενο (εικ. 6.19).

εικ. 6.19

Στη συνέχεια θα ασχοληθούμε με την κατασκευή των πιο απλών πολυγώνων όταν γνωρίζουμε τον κύκλο μέσα στον οποίο εγγράφονται. Οι μέθοδοι που προτείνονται βασίζονται σε απλές γεωμετρικές κατασκευές. Αν ανακαλέσουμε γνώσεις από τη Γεωμετρία, θα διαπιστώσουμε ότι υπάρχουν και άλλοι τρόποι επίλυσης. Επίσης δεν πρέπει να ξεχνάμε ότι όπου αυτό είναι δυνατό (π.χ. τετράγωνο, εξάγωνο, οκτάγωνο), απλούστερη αλλά όχι τόσο ακριβής κατασκευή γίνεται με τη χρήση χάρακα και τριγώνου.

6.4.2 Κατασκευή τετραγώνου (εικ. 6.20)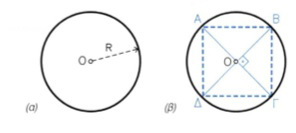

εικ. 6.20

α. Δίδεται κύκλος με ακτίνα R.

β. Φέρω δύο διαμέτρους ΑΓ και ΒΔ κάθετες μεταξύ τους. Τα σημεία τομής με τον κύκλο είναι και κορυφές του τετραγώνου..

6.4.3 Κατασκευή κανονικού πενταγώνου (εικ 6.21)

α. Δίδεται κύκλος με ακτίνα R.

β. Φέρω τη διάμετρο ΑΒ και την κάθετη σ'αυτήν ΓΟ.

γ. Βρίσκω το μέσον Μ της ΟΒ και με κέντρο αυτό και ακτίνα r1, ίση με ΜΓ, γράφω τόξο, που τέμνει την ΑΒ στο Ν. Η ΓΝ είναι ίση με την πλευρά του πενταγώνου,

δ. Με κέντρο το Γ και ακτίνα r2 ίση με ΓΝ γράφω τόξο, που τέμνει τον κύκλο στα Δ και Ε.

ε. Χωρίζω τον κύκλο σε 5 τόξα, που το καθένα αντιστοιχεί σε χορδή ίση με ΓΔ=ΓΕ, ίση με την πλευρά α5 του πενταγώνου. Τα σημεία τομής με τον κύκλο είναι και κορυφές του κανονικού πενταγώνου.

εικ. 6.21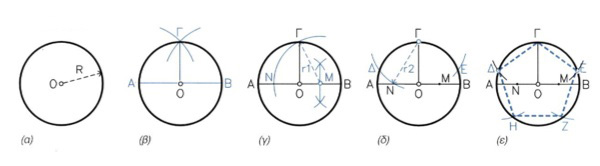

6.4.4 Κατασκευή κανονικού εξαγώνου (εικ 6.22)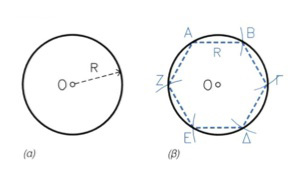

εικ. 6.22

α. Δίδεται κύκλος με ακτίνα R.

β. Ξεκινώντας από σημείο Α του κύκλου και με άνοιγμα διαβήτη ίσο με την ακτίνα R χαράζω 6 διαδοχικά ίσα τόξα. Εκεί όπου τέμνουν τον κύκλο βρίσκονται οι κορυφές του κανονικού εξαγώνου.

6.4.5 Κατασκευή οποιουδήποτε κανονικού πολυγώνου όταν γνωρίζω τον αριθμό των πλευρών του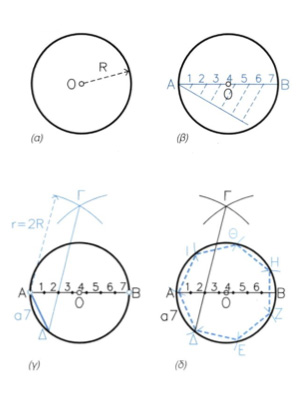

εικ. 6.23

Παράδειγμα: Έστω ότι ζητώ να χαράξω κανονικό επτάγωνο (εικ. 6.23).

α. Δίδεται κύκλος με ακτίνα R.

β. Φέρω διάμετρο ΑΒ και τη διαιρώ σε επτά ίσα τμήματα.

γ. Με ακτίνα r ίση με τη διάμετρο και με κέντρα τα σημεία Α και Β γράφω τόξα, που τέμνονται στο Γ. Στη συνέχεια, φέρω ευθεία, που περνά από το Γ και από το δεύτερο σημείο διαίρεσης της διαμέτρου ΑΒ, μέχρι να τμήσει τον κύκλο στο σημείο Δ.

δ. Η ΑΔ είναι η πλευρά α7 του ζητούμενου κανονικού επταγώνου. Με άνοιγμα διαβήτη ίσο με α7 χωρίζω τον κύκλο σε επτά διαδοχικά τόξα. Τα σημεία τομής τους με τον κύκλο είναι οι κορυφές του επταγώνου.

Με τον ίδιο τρόπο, μπορώ να κατασκευάσω οποιοδήποτε άλλο κανονικό πολύγωνο.