| Μέρος Β' - Κεφάλαιο 2ο - Συμμετρία |
| |
| Β.2.5. Κέντρο συμμετρίας |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ |
 |
|
Βρες ένα σημείο, σε κάθε ένα από τα παρακάτω
σχήματα, γύρω από το οποίο προσπάθησε να περιστρέψεις το σχήμα αυτό
κατά 180° και να παρατηρήσεις εάν συμπίπτει ή όχι με τον εαυτό του,
μετά την ολοκλήρωση της περιστροφής αυτής.

|
Μικροπείραμα  |
|
| |
|
 |
- Κέντρο συμμετρίας σχήματος
ονομάζεται ένα
σημείο του Ο, γύρω από το οποίο αν περιστραφεί το
σχήμα κατά 180°,
συμπίπτει με το αρχικό. Στην περίπτωση που υπάρχει τέτοιο σημείο, λέμε
ότι το
σχήμα έχει κέντρο συμμετρίας το σημείο Ο.
- Όταν ένα σχήμα έχει κέντρο συμμετρίας, το
συμμετρικό του ως προς το κέντρο αυτό είναι το ίδιο το σχήμα.
|
|
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ -
ΕΦΑΡΜΟΓΕΣ |
 |
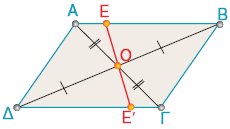
Το συμμετρικό παραλληλογράμμου ΑΒΓΔ, ως προς κέντρο συμμετρίας το
σημείο
τομής των διαγωνίων του, είναι το ίδιο το παραλληλόγραμμο. |
 |
|
|
Παρατηρούμε,
ότι ένα σημείο Ε του
παραλληλογράμμου, με στροφή κατά 180° γύρω από το Ο,
θα συμπέσει
με ένα άλλο σημείο Ε' του ίδιου του
παραλληλογράμμου. Αυτό συμβαίνει για
όλα τα σημεία του ΑΒΓΔ, επομένως το συμμετρικό του
ως προς το Ο είναι
πάλι το ίδιο το παραλληλόγραμμο ΑΒΓΔ.
Μικροπείραμα  |
|
|
 |
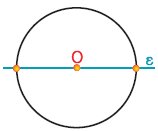
Ποιο είναι το κέντρο συμμετρίας ενός κύκλου; |
|
 |
|
|
Με στροφή κατά 180° γύρω από το κέντρο Ο του κύκλου,
διαπιστώνουμε ότι αυτός συμπίπτει με τον εαυτό του. Επομένως: |
|
- Το κέντρο του κύκλου είναι κέντρο
συμμετρίας του καθώς και του αντίστοιχου κυκλικού δίσκου.
|
 |
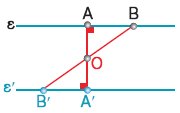
Να αποδειχθεί ότι το
συμμετρικό σχήμα μιας ευθείας ε, ως προς κέντρο Ο, είναι ευθεία ε'//ε. |
 |
|
|
Φέρνουμε
την απόσταση ΟΑ του Ο από την ε.
Έστω Β ένα άλλο σημείο της ε.
Βρίσκουμε τα συμμετρικά Α' και Β' των σημείων Α και Β ως προς το Ο και
ονομάζουμε ε' την ευθεία που διέρχεται από τα Α' και Β'. Η
ευθεία ε' είναι συμμετρική της ε ως προς κέντρο συμμετρίας το Ο.
Η γωνία ΟÂ'Β' θα είναι συμμετρική της γωνίας ΟÂΒ. Επειδή
οι συμμετρικές γωνίες είναι ίσες, θα είναι: ΟÂ'Β'=ΟÂΒ=90°.
Άρα, οι
ευθείες ε και ε' είναι κάθετες
στην ίδια ευθεία ΑΑ',
συνεπώς μεταξύ τους παράλληλες. |
|
|
- Οι συμμετρικές ως προς σημείο ευθείες,
είναι μεταξύ τους παράλληλες.
|
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ
ΠΡΟΒΛΗΜΑΤΑ |
 |
Αφού γράψεις τα κεφαλαία γράμματα του αλφαβήτου, εξέτασε αν έχουν
κέντρο συμμετρίας.
Μικροπείραμα  |

|
 |
Να βρεις στα παρακάτω σχήματα το κέντρο
συμμετρίας, αν υπάρχει.

|
 |
Τοποθέτησε ένα "Χ" στις
κατάλληλες θέσεις, για τη θετική σου απάντηση.
| |
Άξονες συμμετρίας |
Έχει
Κέντρο
Συμμετρίας |
| |
Κανένα |
Ένα |
Δύο |
Τρεις |
Τέσσερις |
Περισσότερους |
| Ευθύγραμμο
τμήμα |
|
|
|
|
|
|
|
| Ισοσκελές
τρίγωνο |
|
|
|
|
|
|
|
| Ισόπλευρο
τρίγωνο |
|
|
|
|
|
|
|
| Παραλληλόγραμμο |
|
|
|
|
|
|
|
| Ορθογώνιο |
|
|
|
|
|
|
|
| Ρόμβος |
|
|
|
|
|
|
|
| Τετράγωνο |
|
|
|
|
|
|
|
| Κύκλος |
|
|
|
|
|
|
|
|
|