Β.2.2. Άξονας συμμετρίας

Μέρος Β' - Κεφάλαιο 2ο - Συμμετρία

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

Σχεδίασε σ' ένα διαφανές χαρτί μια ευθεία. Τοποθέτησε το διαφανές αυτό χαρτί πάνω σε καθένα από τα παρακάτω σχήματα. Εξέτασε αν υπάρχει θέση τέτοια που τα δύο μέρη, στα οποία η ευθεία "χωρίζει" το σχήμα, συμπίπτουν, όταν το διπλώσεις κατά μήκος της ευθείας, ακριβώς στη θέση αυτή.

Προσπάθησε να βρεις αν υπάρχει και άλλη θέση στην οποία μπορείς να παρατηρήσεις το ίδιο φαινόμενο για το ίδιο σχήμα.

Μικροπείραμα Μικροπείραμα

Θυμόμαστε - Μαθαίνουμε

Άξονας συμμετρίας σχήματος ονομάζεται η ευθεία που χωρίζει το σχήμα σε δύο μέρη, τα οποία συμπίπτουν όταν διπλωθεί το σχήμα κατά μήκος της ευθείας. Στην περίπτωση αυτή λέμε ότι το σχήμα έχει άξονα συμμετρίας την ευθεία αυτή.
- Όταν ένα σχήμα έχει άξονα συμμετρίας, το συμμετρικό του ως προς τον άξονα αυτόν είναι το ίδιο το σχήμα.

ΠΑΡΑΔΕΙΓΜΑ - ΕΦΑΡΜΟΓΗ

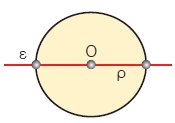
Να βρεθούν οι άξονες συμμετρίας του κύκλου και του αντίστοιχου κυκλικού δίσκου (Ο,ρ).

Μικροπείραμα

Με δίπλωση διαπιστώνουμε ότι η ευθεία ε πάνω στην οποία βρίσκεται μια οποιαδήποτε διάμετρος του κύκλου (Ο,ρ) είναι άξονας συμμετρίας του κύκλου και του αντίστοιχου κυκλικού δίσκου.

Eπομένως:

Οποιαδήποτε ευθεία διέρχεται από το κέντρο του κύκλου είναι άξονας συμμετρίας του κύκλου και του αντίστοιχου κυκλικού δίσκου.

ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ

	Να επιλέξεις τη σωστή απάντηση: Κάθε κύκλος και ο αντίστοιχος κυκλικός δίσκος έχουν: Ένα άξονα συμμετρίας Άπειρους άξονες συμμετρίας Κανένα άξονα συμμετρίας.
	Εξέτασε αν τα κεφαλαία γράμματα του αλφαβήτου A, I, Γ και Θ έχουν: (α) κανένα, (β) ένα, (γ) περισσότερους από ένα άξονες συμμετρίας. Μικροπείραμα
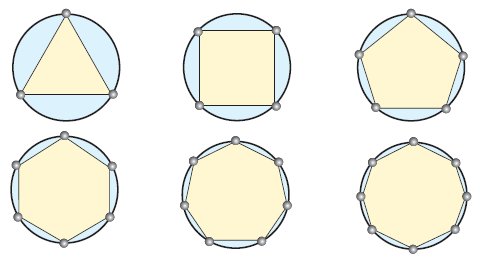
	Σχεδίασε τους άξονες συμμετρίας των παρακάτω γεωμετρικών σχημάτων Μικροπείραμα
	Σχεδίασε τους άξονες συμμετρίας του σχήματος που δημιουργείται από δύο ίσους τεμνόμενους κύκλους. Μικροπείραμα
	Βρες τους άξονες συμμετρίας του σχήματος που δημιουργείται από δύο κύκλους με διαφορετικές ακτίνες, όταν: (α) έχουν το ίδιο κέντρο και (β) έχουν διαφορετικά κέντρα. Μικροπείραμα