Β.2.1. Συμμετρία ως προς άξονα

Μέρος Β' - Κεφάλαιο 2ο - Συμμετρία

Τι είναι συμμετρία; Ο ποιητής θα έλεγε: ό,τι φοριέται από την ανάποδη. Ό,τι διπλώνει και ταιριάζει, ό,τι στρίβει και "συμπίπτει". Μόνο η φαντασία δεν έχει καθόλου συμμετρία. Γι' αυτό η συμμετρία χρειάζεται και λίγη φαντασία. Αν αυτή ακριβώς τη φαντασία τη φορέσουμε ανάποδα, θα μας βγει όλη η Γεωμετρία.

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

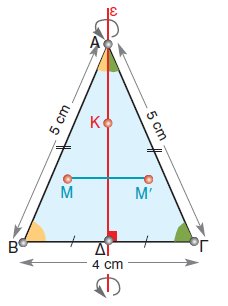
Κατασκεύασε ένα ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ = 5 cm και ΒΓ = 4 cm και τη διάμεσό του ΑΔ.

Δίπλωσε το σχήμα κατά μήκος της ευθείας ε που ανήκει η ΑΔ.

Τι παρατηρείς;

Μικροπείραμα Μικροπείραμα

Σκεφτόμαστε

Παρατηρούμε ότι τα τρίγωνα ΑΒΔ και ΑΓΔ συμπίπτουν. Αυτό σημαίνει, ότι κάθε σημείο του ενός τριγώνου συμπίπτει με ένα σημείο του άλλου τριγώνου. Για παράδειγμα, το Β συμπίπτει με το Γ. Τα σημεία αυτά λέγονται συμμετρικά ως προς άξονα συμμετρίας την ευθεία ε.

Με τη δίπλωση κατά μήκος της ευθείας ε, κάθε σημείο της συμπίπτει με τον εαυτό του. Επομένως συμμετρικό του Α είναι το Α, του Δ το Δ και ενός οποιουδήποτε σημείου Κ της ε το ίδιο το Κ.

Θυμόμαστε - Μαθαίνουμε

Συμμετρικό σημείου Β ως προς ευθεία ε, είναι το σημείο Γ με το οποίο συμπίπτει το Β, αν διπλώσουμε το φύλλο κατά μήκος της ευθείας ε.
Κάθε σημείο μιας ευθείας ε είναι συμμετρικό του εαυτού του ως προς την ε.

Όπως είδαμε, με τη δίπλωση κατά μήκος της ευθείας ε κάθε σημείο του τριγώνου ΑΒΔ συμπίπτει με ένα σημείο του τριγώνου ΑΓΔ. Αυτό σημαίνει ότι καθένα από τα τρίγωνα αυτά αποτελείται από τα συμμετρικά όλων των σημείων του άλλου τριγώνου ως προς την ευθεία ε.

Γι' αυτό λέμε ότι:

Τα τρίγωνα ΑΒΔ και ΑΓΔ είναι συμμετρικά ως προς την ευθεία ε

Γενικότερα:

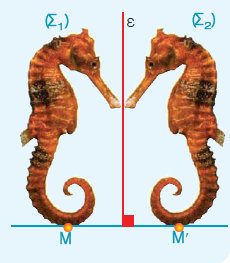
Δύο σχήματα (Σ₁) και (Σ₂) λέγονται συμμετρικά ως προς μία ευθεία ε, όταν καθένα αποτελείται από τα συμμετρικά σημεία του άλλου ως προς την ε.

Επειδή με δίπλωση κατά μήκος της ε συμπίπτει το (Σ₁) με το (Σ₂), γνωρίζουμε ότι αυτά θα είναι ίσα. Επομένως:

Τα συμμετρικά ως προς ευθεία σχήματα είναι ίσα.

ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ

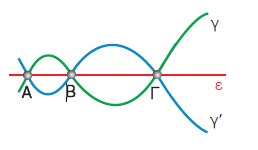
Μια γραμμή γ τέμνει την ευθεία ε στα σημεία Α, Β και Γ. Να βρεθεί ο λόγος για τον οποίο και η συμμετρική γ' της γ, ως προς την ευθεία ε, θα περνάει από τα ίδια σημεία.

Η συμμετρική γραμμή γ' της γ ως προς την ε, αποτελείται από τα συμμετρικά όλων των σημείων της γ. Επομένως στη γ' ανήκουν και τα συμμετρικά σημεία των Α, Β και Γ. Επειδή όμως τα Α, Β και Γ είναι σημεία της ε τα συμμετρικά τους είναι τα ίδια τα σημεία. Άρα τα Α, Β και Γ ανήκουν και στη γ'.

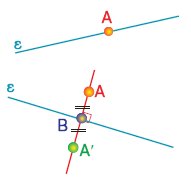
Να κατασκευαστεί το συμμετρικό Α' σημείου Α ως προς μια ευθεία ε.

Διακρίνουμε δύο περιπτώσεις:

Το σημείο Α ανήκει στην ευθεία ε. Τότε, όπως είδαμε, το συμμετρικό του είναι το ίδιο το σημείο Α.
Το σημείο Α δεν ανήκει στην ευθεία ε. Τότε, για να βρούμε το συμμετρικό του, ακολουθούμε την παρακάτω διαδικασία: Φέρνουμε το κάθετο τμήμα ΑΒ από το σημείο Α προς την ευθεία ε και το προεκτείνουμε κατά ίσο τμήμα, ώστε να είναι
ΒΑ' = ΑΒ. Το σημείο Α' είναι το συμμετρικό του Α ως προς την ευθεία ε.

Μικροπείραμα

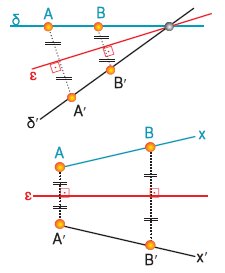
Να κατασκευαστεί η συμμετρική ως προς ευθεία ε: (α) ευθείας δ και (β) ημιευθείας Αx.

(α)	Παίρνουμε δύο σημεία Α και Β πάνω στην ευθεία δ και βρίσκουμε, όπως περιγράφεται στην εφαρμογή 3, τα συμμετρικά τους Α' και Β', ως προς την ε. Η ευθεία δ' που ορίζουν τα Α' και Β' είναι η συμμετρική της ευθείας δ.
(β)	Παρόμοια παίρνουμε, εκτός του Α, ένα δεύτερο σημείο Β πάνω στην ημιευθεία Αx και βρίσκουμε, όπως πριν, τα συμμετρικά τους Α' και Β' ως προς την ε. Η ημιευθεία Α'x' που ορίζουν τα Α' και Β' είναι η συμμετρική της ημιευθείας Αx

Μικροπείραμα

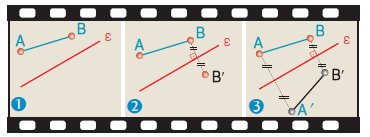
Να κατασκευαστεί το συμμετρικό Α'Β' ενός ευθύγραμμου τμήματος ΑΒ, ως προς μια ευθεία ε.

Βρίσκουμε με τον τρόπο που είδαμε στην εφαρμογή 3, τα συμμετρικά Α' και Β', ως προς την ε, των Α και Β αντίστοιχα. Τότε το ευθύγραμμο τμήμα Α'Β' θα είναι το συμμετρικό του ΑΒ, ως προς την ευθεία ε.Τα συμμετρικά ευθύγραμμα τμήματα θα είναι μεταξύ τους ίσα, δηλαδή: Α'Β' = ΑΒ

Μικροπείραμα

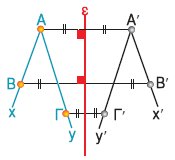
Να κατασκευαστεί η συμμετρική γωνίας xÂy ως προς μία ευθεία ε.

Για να κατασκευάσουμε τη γωνία x'Â'y'αρκεί να βρούμε το συμμετρικό Α' της κορυφής Α καθώς και τα συμμετρικά Β' και Γ' δύο ακόμα σημείων Β και Γ, που ανήκουν το καθένα σε μια από τις πλευρές της αντίστοιχα.
Γνωρίζουμε ότι θα είναι: x'Â'y' = xÂy.

Να κατασκευαστεί το συμμετρικό Α'Β'Γ’ ενός τριγώνου ΑΒΓ ως προς μία ευθεία ε, η οποία (α) δεν τέμνει τις πλευρές του, (β) διέρχεται από δύο κορυφές του και (γ) τέμνει τις πλευρές του.

Σε κάθε περίπτωση βρίσκουμε τα συμμετρικά Α', Β', Γ', ως προς την ε, των κορυφών Α, Β, Γ του τριγώνου. Τότε το τρίγωνο ΑΒΓ έχει συμμετρικό το τρίγωνο Α'Β'Γ', που είναι ίσο με το ΑΒΓ.


(Η ε δεν τέμνει τις πλευρές)	(Η ε διέρχεται από τα Β και Γ)	(Η ε τέμνει τις πλευρές)

Μικροπείραμα

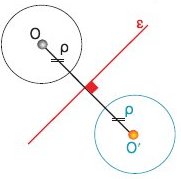
Να κατασκευαστεί το συμμετρικό κύκλου (Ο, ρ) ως προς ευθεία ε.

Το συμμετρικό του κύκλου (Ο, ρ) ως προς την ε είναι κύκλος (Ο', ρ) ίσος με τον (Ο, ρ), με Ο' συμμετρικό του Ο ως προς την ε. Όπως όλα τα συμμετρικά σχήματα, οι κύκλοι
(Ο, ρ) και (Ο', ρ) είναι ίσοι, δηλαδή έχουν ίσες ακτίνες.

Μικροπείραμα

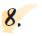Να χαραχθεί η πορεία των ακτίνων του φωτός, που εκπέμπονται από ένα φωτεινό σημείο Α και ανακλώνται σ' έναν επίπεδο καθρέφτη (ο οποίος στο σχήμα φαίνεται ως μία ευθεία ε).

Βρίσκουμε το συμμετρικό Α' του σημείου Α ως προς την ευθεία ε. Οι ακτίνες ανακλώνται στον καθρέφτη και ακολουθούν την πορεία, που θα είχαν, αν η πηγή του φωτός ήταν το σημείο Α'. Επειδή οι γωνίες που σχηματίζουν οι ακτίνες με την ε είναι συμμετρικές, θα είναι και ίσες. Άρα, η γωνία με την οποία μια ακτίνα πέφτει στον καθρέφτη είναι ίση με τη γωνία με την οποία ανακλάται.

Μικροπείραμα

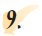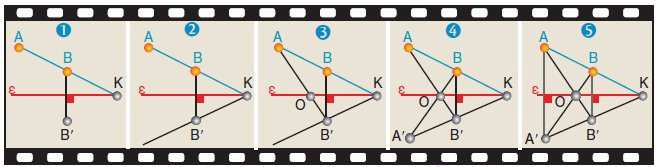
Στο σχήμα τα σημεία Β και Β' είναι συμμετρικά ως προς την ευθεία ε. Να βρεθεί με τη βοήθεια μόνο του χάρακα το συμμετρικό του Α ως προς την ευθεία ε.

Επειδή με το χάρακα μπορούμε να φέρουμε μόνο ευθείες γραμμές, ακολουθούμε τα παρακάτω βήματα, όπως φαίνονται στο διπλανό σχήμα:

Φέρνουμε την ευθεία ΑΒ και την προεκτείνουμε μέχρι να τμήσει τον άξονα ε στο σημείο Κ
Φέρνουμε την ευθεία ΚΒ', η οποία είναι συμμετρική της ΚΒ, αφού ενώνει δύο συμμετρικά σημεία αυτής, τα Κ και Β'.
Φέρνουμε την ΑΒ', που τέμνει την ε στο Ο.
Τέλος, φέρνουμε την ΒΟ, που η συμμετρική της είναι η ΟΒ'.

Οι ευθείες ΚΒ' και ΒΟ είναι συμμετρικές των ΚΒ και Β'Ο αντίστοιχα και οι τομές τους θα είναι συμμετρικά σημεία, τα Α και Α'.

ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ

Εικόνα

Να βρεις τη συμμετρική της γωνίας xÔy ως προς την ευθεία ε, σε καθεμιά από τις δύο περιπτώσεις.

Εικόνα

Να βρεις το συμμετρικό του κύκλου (Ο, ρ) ως προς την ευθεία ε σε καθεμιά από τις δύο περιπτώσεις.

Μικροπείραμα

Εικόνα

Να βρεις το συμμετρικό του σχήματος ως προς την ευθεία ε και το συμμετρικό του νέου σχήματος ως προς την ευθεία ε', η οποία είναι παράλληλη με την ε. Τι σχέση έχουν το αρχικό και το τελευταίο σχήμα; Να επαναλάβεις το ίδιο και με μια τρίτη παράλληλη. Τι παρατηρείς;

Μικροπείραμα

Εικόνα

ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΠΑ ΤΟ ΣΠΙΤΙ

	Βρες το συμμετρικό ενός τριγώνου ως προς μια ευθεία ε και το συμμετρικό του νέου τριγώνου ως προς μία άλλη ευθεία ζ. Τι σχέση έχουν το αρχικό και το τελευταίο τρίγωνο; Να επαναλάβεις το ίδιο και με τρίτη ευθεία.
	Προσπάθησε να δείξεις, ότι το συμμετρικό σχήμα ως προς άξονα δ μιας ευθείας ε παράλληλης προς τη δ, είναι ευθεία παράλληλη προς την ευθεία ε.