Β.1.6. Είδη γωνιών – Κάθετες ευθείες

Μέρος Β' - Κεφάλαιο 1ο - Βασικές γεωμετικές έννοιες

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η

Σε όλα τα παρακάτω αντικείμενα σχηματίζονται διάφορες γωνίες ανάλογα με τη σχετική θέση, κάθε φορά, δύο ημιευθειών που έχουν ένα κοινό σημείο, όπως π.χ. είναι οι δείκτες του ρολογιού, τα πόδια των ανθρώπων, τα φτερά του αετού κ.λπ.

Η σειρά που τοποθετήθηκαν τα διάφορα σκίτσα είναι τυχαία.

Μπορείς να βρεις τη σωστή αντιστοιχία;

Μικροπείραμα

Εικόνα

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η

Το σπίτι της διπλανής εικόνας έχει δύο καμινάδες.

Ποια είναι η μεταξύ τους διαφορά;
Ποια από τις δύο είναι κάθετη στη στέγη και γιατί;
Γενικότερα, είναι δυνατό να έχουμε κάθετες ευθείες, χωρίς απαραίτητα να είναι αυτές οριζόντιες και κατακόρυφες;

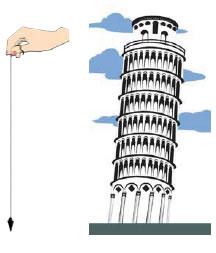Ξέρεις γιατί δε πέφτει ο πύργος της Πίζας;
Πώς βρίσκουμε την κατακόρυφο σε ένα τόπο;
Και πώς ελέγχουμε ότι ένα επίπεδο έχει οριζόντια θέση;

Μικροπείραμα Μικροπείραμα

Θυμόμαστε - Μαθαίνουμε

Είδη γωνιών

Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90^ο
- Οι πλευρές της ορθής γωνίας είναι κάθετες ημιευθείες

Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90^ο

Αμβλεία γωνία λέγεται κάθε γωνία με μέτρο μεγαλύτερο των 90^ο και μικρότερο των 180^ο

Εικόνα

Ευθεία γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 180^ο
- Οι πλευρές της ευθείας γωνίας είναι αντικείμενες ημιευθείες.

Μη κυρτή γωνία λέγεται κάθε γωνία με μέτρο μεγαλύτερο των 180^ο και μικρότερο των 360^ο

Μηδενική γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 0^ο

Πλήρης γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 360^ο

Η ημιευθεία της τελικής πλευράς μιας μηδενικής και μιας πλήρους γωνίας ταυτίζεται με αυτή της αρχικής πλευράς.

Δύο ευθείες είναι κάθετες όταν οι γωνίες που σχηματίζουν αυτές τεμνόμενες, είναι ορθές.

Πώς συμβολίζουμε την καθετότητα δύο ευθειών

Για να δηλώσουμε ότι δύο ευθείες ε₁ και ε₂ είναι κάθετες χρησιμοποιούμε το σύμβολο «», γράφουμε ε₁ ε₂ και διαβάζουμε «η ε₁ είναι κάθετη στην ε₂».
Δύο ευθύγραμμα τμήματα (ή δύο ημιευθείες) που βρίσκονται πάνω σε δύο κάθετες ευθείες, λέγονται κάθετα ευθύγραμμα τμήματα (ή κάθετες ημιευθείες).

Μικροπείραμα Μικροπείραμα

ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ

Πως μπορούμε να διαπιστώσουμε ότι δύο τεμνόμενες ευθείες είναι κάθετες;

Σχεδιάζουμε δύο τεμνόμενες ευθείες ε₁ και ε₂ σε ένα φύλλο χαρτί.

Διπλώνουμε το χαρτί κατά μήκος της ευθείας ε₂ και διακρίνουμε δύο περιπτώσεις:

(α)

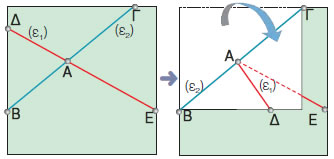Οι ημιευθείες ΑΔ και ΑΕ δεν συμπίπτουν.

Επομένως οι τεμνόμενες ευθείες ε₁ και ε₂ δεν είναι κάθετες.

(β)

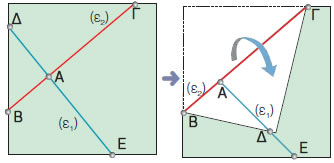Οι ημιευθείες ΑΔ και ΑΕ συμπίπτουν. Στην περίπτωση αυτή λέμε ότι οι τεμνόμενες ευθείες ε₁ και ε₂ είναι κάθετες (ε₁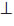 Εικόνα

ε₂).

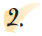Πως μπορούμε να κατασκευάσουμε δύο κάθετες ευθείες;

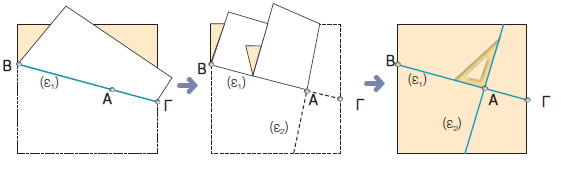
Αν διπλώσουμε το φύλλο χαρτί δύο φορές, με τον τρόπο που φαίνεται στα παρακάτω σχήματα και μετά το ανοίξουμε, παρατηρούμε ότι τα τσακίσματα, που έγιναν πάνω στο χαρτί, παριστάνουν δύο κάθετες ευθείες ε₁, και ε₂.

Εικόνα

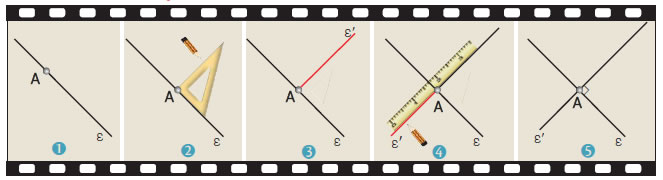
Να σχεδιαστεί ευθεία ε΄, που διέρχεται από σημείο Α και είναι κάθετη σε ευθεία ε.

1η περίπτωση: Το σημείο Α ανήκει στην ε

Εικόνα

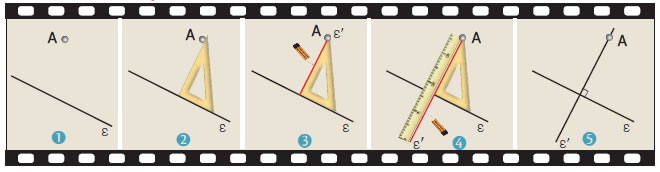
2η περίπτωση: Το σημείο Α δεν ανήκει στην ε

Εικόνα

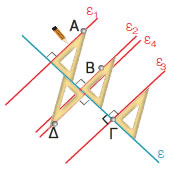
Δίνεται η ευθεία ε και τα σημεία Α, Β, Γ και Δ. Να σχεδιαστούν ευθείες ε₁, ε₂, ε₃ και ε₄, που διέρχονται από αυτά τα σημεία αντίστοιχα, κάθετες στην ε.

Τοποθετούμε τον γνώμονα πάνω στην ευθεία ε έτσι, ώστε η μία από τις δύο κάθετες πλευρές του να συμπίπτει με την ευθεία ε. Σύρουμε τον γνώμονα στην ευθεία ε, έως ότου η άλλη κάθετη πλευρά του να έρθει σε επαφή με ένα από τα δοσμένα σημεία. Από το σημείο αυτό χαράζουμε την ευθεία που είναι κάθετη στην ε. Επαναλαμβάνουμε τη διαδικασία αυτή, για κάθε σημείο Α, Β, Γ και Δ και κατασκευάζουμε τις ευθείες ε₁, ε₂, ε₃ και ε₄ αντίστοιχα, που είναι κάθετες στην ευθεία ε.

ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ

Τοποθέτησε ένα "x" στη θέση που αντιστοιχεί στη σωστή απάντηση.

(α)	Αν οι πλευρές μιας γωνίας είναι ημιευθείες κάθετες μεταξύ τους, τότε η γωνία λέγεται: Οξεία Ορθή Αμβλεία.
(β)	Αν σε μια γωνία η τελική πλευρά της ταυτίζεται με την αρχική, αφού κάνει μια πλήρη στροφή, τότε η γωνία λέγεται: Μηδενική γωνία Ευθεία γωνία Πλήρης γωνία.

Σχεδίασε ημιευθεία Οχ και χάραξε ευθεία που να διέρχεται από το Ο κάθετη στην Οχ

Σχεδίασε δύο ευθείες που να διέρχονται από τα άκρα ενός ευθύγραμμου τμήματος και να είναι κάθετες σ' αυτό.

Σχεδίασε δύο ημιευθείες Οχ και Οy που να μην περιέχονται στην ίδια ευθεία. Σημείωσε στην ΟΧ τρία σημεία Α, Β και Γ. Από κάθε σημείο από αυτά σχεδίασε ευθεία κάθετη προς την Οy.

Σχεδίασε δύο ημιευθείες Οχ και Οy που να μην περιέχονται στην ίδια ευθεία. Στο σημείο Ο να φέρεις τις κάθετες ευθείες προς τις Οχ και Οy. Τι παρατηρείς;

Σχεδίασε ένα τρίγωνο και φέρε από κάθε κορυφή του την κάθετη προς την απέναντι πλευρά του.

Σχεδίασε μια ευθεία ε και δύο σημεία Α και Β που δεν ανήκουν στην ευθεία αυτή. Φέρε από τα Α και Β ευθείες κάθετες προς την ε και εξέτασε σε ποια περίπτωση οι δύο αυτές κάθετες συμπίπτουν.

Τοποθέτησε τις παρακάτω ονομασίες γωνιών, με σειρά μεγέθους του μέτρου τους: Ορθή - Ευθεία - Πλήρης - Αμβλεία - Μηδενική - Μη κυρτή - Οξεία.

Μικροπείραμα