| Β.1.3. Μέτρηση, σύγκριση και ισότητα
ευθυγράμμων τμημάτων – Απόσταση σημείων – Μέσο ευθύγραμμου τμήματος |
Στα προηγούμενα είδαμε τον τρόπο με τον οποίο
διαπιστώνουμε την ισότητα δύο γεωμετρικών σχημάτων. Το απλούστερο
σχήμα, του οποίου το μήκος μπορεί να μετρηθεί, είναι το ευθύγραμμο
τμήμα και αποτελεί βασικό στοιχείο των άλλων ευθυγράμμων σχημάτων. Τι
είναι όμως μέτρηση και μονάδες μήκους; |
| |
| ΙΣΤΟΡΙΚΗ ΑΝΑΔΡΟΜΗ |
 |
|
| |
Από τα πολύ παλιά χρόνια, οι ανάγκες της ζωής,
υποχρέωσαν τους ανθρώπους να μετρήσουν διάφορα μεγέθη. Για να
εξυπηρετούν οι μετρήσεις αυτές έπρεπε να χρησιμοποιηθούν σταθερά
υποδείγματα, τα οποία να διαθέτει ο καθένας οποιαδήποτε στιγμή τα
χρειαζόταν. Αρχικά στη μέτρηση χρησιμοποιήθηκαν τα μέλη του ανθρώπινου
σώματος αλλά και ο βηματισμός, το άνοιγμα των χεριών και το ύψος. Έτσι,
δημιουργήθηκαν οι μονάδες, όπως: οι "δάκτυλοι", οι "πόδες"
οι "παλάμες" κ.α. Αυτή την παλιά συνήθεια
εξακολουθούμε να εφαρμόζουμε και σήμερα στις πρόχειρες μετρήσεις μας:
"Το πανταλόνι θέλει δυο δάκτυλα μάκρεμα", "Το χορτάρι ψήλωσε μια
πιθαμή", "Το σκάφος έχει μήκος 40 πόδια", "Τα δίκτυα έφτασαν στις 50
οργιές", "Βάλε στο ποτήρι ένα δάκτυλο κρασί", "Το πέναλτι χτυπιέται στα
11 βήματα", κ.λπ. Οι μονάδες αυτές, αν και πολύ χρήσιμες, άρχισαν να
χάνουν την αξία τους διότι δεν είναι ακριβείς, αφού όλοι οι άνθρωποι
δεν έχουν το ίδιο ύψος, την ίδια παλάμη, το ίδιο πάχος δακτύλων και το
ίδιο άνοιγμα στο βήμα τους. Όσο όμως αναπτύσσονταν οι ανθρώπινες
κοινωνίες τόσο μεγαλύτερη ακρίβεια χρειάζονταν ορισμένες μετρήσεις,
όπως π.χ. για το κτίσιμο των σπιτιών, την κατασκευή αρδευτικών έργων,
την καταμέτρηση της γης, κ.λπ. Στην αρχαία Αίγυπτο,
μετά από κάθε πλημμύρα του Νείλου, η λάσπη κάλυπτε τα σύνορα των
κτημάτων. Υπήρχαν τότε ειδικοί υπάλληλοι, οι "αρπεδονάπτες", οι οποίοι
επόπτευαν την τήρηση του διαχωρισμού των εκτάσεων. Στις καταμετρήσεις
αυτές λέγεται ότι έκαναν μ' ένα ειδικό σχοινί με κόμπους, την "αρπεδόνη".
 |
Οι αρχαίοι Αιγύπτιοι, από την εποχή του
βασιλέα Σέσωστρη (κατά τον Ηρόδοτο), τηρούσαν
στοιχεία μέτρησης των εκτά σεων που καλλιεργούσαν για να τα
ξαναβρίσκουν μετά τις εποχιακές πλημμύρες του Νείλου ποταμού.
Άλλωστε Γεω - μετρία σημαίνει μέτρηση της Γης. Αλλά και οι Βαβυλώνιοι χρησιμοποιούσαν
συγκεκριμένα υποδείγματα για να υπολογίσουν το εμβαδόν και τον όγκο σε
πολλά πράγματα καθημερινής χρήσης. |
| Όταν
αναπτύχθηκε η επικοινωνία λαών και κρατών, με τα ταξίδια και το
εμπόριο, δημιουργήθηκε η ανάγκη να καθιερωθούν κοινές μονάδες μέτρησης
για καλύτερη συνεννόηση και αποφυγή της ταλαιπωρίας των μετατροπών απ'
τη μία μονάδα στην άλλη, όπως π.χ. στην αρχαία Αθήνα από τον Σόλωνα. |
 |
 |
Το 1791,
αμέσως μετά την Επανάσταση, η Γαλλική Ακαδημία ανέθεσε σε μια ομάδα επιστημόνων, απ' όλες τις χώρες της Ευρώπης, να
βρουν ένα απλό σύστημα μονάδων μέτρησης. Οι μονάδες που υιοθετήθηκαν
τελικά πάρθηκαν από τη φύση και για παράδειγμα η μέτρηση του μήκους
καθιερώθηκε να έχει μονάδα το "μέτρο", που είναι το 1 από τα
40.000.000 ίσα κομμάτια που χωρίστηκε ο γήινος μεσημβρινός που
διέρχεται από το Παρίσι. Το σύστημα των μονάδων ακολουθεί το
δεκαδικό σύστημα αρίθμησης, δηλαδή είναι ένα δεκαδικό μετρικό σύστημα.
Μετά από ένα αργό ξεκίνημα, το σύστημα αυτό καθιερώθηκε και το 1875 ιδρύθηκε στη Σεβρ (στο Παρίσι) το Διεθνές
Γραφείο Μέτρων και Σταθμών, όπου φυλάχτηκαν τα κατασκευασμένα
από πλατίνα πρότυπα "μέτρο" και "χιλιόγραμμο". |
Το σύστημα αυτό των μονάδων δεν υιοθετήθηκε αμέσως
απ' όλους τους λαούς, που προτίμησαν να χρησιμοποιούν τα δικά τους
συστήματα, όπως τα είχαν συνηθίσει, παρ' όλο που ήταν πιο πολύπλοκα.
Στη νεώτερη Ελλάδα, καθιερώθηκε με νόμο, το 1959,
το δεκαδικό μετρικό σύστημα και ισχύει μέχρι σήμερα.
 |
Στην Αγγλία, την Αμερική και σε μερικές ακόμη χώρες, το σύστημα μέτρησης είναι δωδεκαδικό και η
βασική μονάδα μήκους είναι η υάρδα ή γιάρδα
(yd). Η 1 γιάρδα (yd) διαιρείται σε 3
πόδια (ft), και το 1 πόδι (ft) σε 12
ίντσες (in). Οι σχέσεις των μονάδων αυτών μεταξύ τους αλλά και
με το μέτρο είναι:
| 1yd = 3 ft = 36 in |
1yd = 0,9144 m = 91,44 cm |
| 1 ft = 12 in |
1 ft = 0,3048 m = 30,48 cm |
| |
1 in = 0,0254 m = 2,54 cm |
|
 |
Στις ίδιες χώρες για μέτρηση μεγάλων αποστάσεων
χρησιμοποιούν το μίλι, που είναι: 1 μίλι = 1609 m = 1,609 Km.
Στη ναυτιλία χρησιμοποιούν για μονάδα μήκους το ναυτικό μίλι, που
είναι: 1 ναυτικό μίλι = 1852 m. |
|
| |
| |
Μέτρηση και
μονάδες μέτρησης
- Για να συγκρίνουμε
μεταξύ τους ευθύγραμμα τμήματα οδηγηθήκαμε στην ανάγκη να
χρησιμοποιούμε μια κοινή μονάδα σύγκρισης. Έτσι, κάθε σύγκριση ενός
μεγέθους με την αντίστοιχη μονάδα λέγεται μέτρηση.
Έτσι, για το μήκος έχουμε ότι:
- Μονάδα μήκους είναι το
"μέτρο" (m)
- Για να μετρήσουμε,
λοιπόν, ένα ευθύγραμμο τμήμα, χρησιμοποιούμε ένα αντίγραφο του μέτρου και κάνουμε τη σύγκριση μ' αυτό, όπως έχουμε μάθει.
- Εάν όμως το μήκος
του ευθύγραμμου τμήματος είναι πολύ μεγαλύτερο ή πολύ μικρότερο από το
μήκος του μέτρου, επιλέγουμε, για τη μέτρηση ένα πολλαπλάσιο ή μια υποδιαίρεση του μέτρου για το σκοπό αυτό.
- Για να μετρήσουμε
σχετικά μικρά μήκη χρησιμοποιούμε, συνήθως, το υποδεκάμετρο,
που είναι το ένα δέκατο (
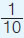 ) του μέτρου. ) του μέτρου.
|
 |
|
 |
- Για μεγαλύτερα μήκη,
όπως π.χ. έναν τοίχο ή τις διαστάσεις ενός οικοπέδου, χρησιμοποιούμε τη μετροταινία.
|
|
|
- Για πολύ μικρά μήκη
π.χ. τη διάμετρο μιας βίδας ή το πάχος μιας λαμαρίνας, χρησιμοποιούμε
το παχύμετρο ή το μικρόμετρο,
αντίστοιχα.
|
| |
ΟΝΟΜΑΣΙΑ ΜΟΝΑΔΑΣ ΜΗΚΟΥΣ |
ΣΥΜΒΟΛΟ |
ΣΧΕΣΗ ΜΕ ΤΟ ΜΕΤΡΟ |
ΠΟΛΛΑΠΛΑΣΙΟ
ΜΕΤΡΟΥ |
Χιλιόμετρο |
Km |
1 Km = 1000 m |
| |
ΜΕΤΡΟ |
m |
|
ΥΠΟΔΙΑΙΡΕΣΕΙΣ ΤΟΥ
ΜΕΤΡΟΥ |
Δεκατόμετρο ή παλάμη |
dm |
1 dm = 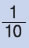 m = 0,1 m m = 0,1 m |
| Εκατοστόμετρο ή πόντος |
cm |
1 cm = 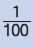 m = 0,01 m m = 0,01 m |
| Χιλιοστόμετρο ή χιλιοστό |
mm |
1 mm = 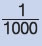 m = 0,001 m m = 0,001 m |
| |
Η
σχέση μεταξύ των υποδιαιρέσεων του μέτρου είναι η εξής: |
| |
|
1 m |
= 10 dm |
= 100 cm |
= 1000 mm |
| |
|
|
1 dm |
= 10 cm |
= 100 mm |
| |
|
|
|
1 cm |
= 10 mm |
|
|
| |
H έννοια της απόστασης σημείων είναι από τις πιο
συνηθισμένες γεωμετρικές έννοιες, που συναντάμε στην ζωή π.χ. απόσταση
δύο πόλεων κ.λ.π.
Πώς όμως ορίζεται η απόσταση δύο σημείων και πως την
μετράμε; |
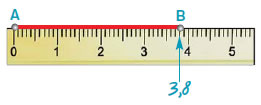 |
- Έχουμε
τα σημεία Α και Β. Χαράζουμε το
ευθύγραμμο τμήμα ΑΒ και το μετράμε με το
υποδεκάμετρο. Βρίσκουμε ότι έχει μήκος 3,8 cm.
- Λέμε
ότι η απόσταση των σημείων Α και Β είναι 3,8 cm και γράφουμε ΑΒ = 3,8 cm.
|
|
| |
 |
Συνεπώς:
- Απόσταση δύο σημείων Α και Β λέγεται το
μήκος του ευθύγραμμου τμήματος ΑΒ, που τα ενώνει.
Πρέπει, όμως, να προσέξουμε κάτι σημαντικό:
- Με το σύμβολο ΑΒ εννοούμε ταυτόχρονα δύο διαφορετικά πράγματα: Το ευθύγραμμο
τμήμα ΑΒ, αλλά και το μήκος αυτού του
ευθύγραμμου τμήματος ΑΒ.
- Για να ξεχωρίσουμε το
μήκος, συνήθως χρησιμοποιούμε τον συμβολισμό (ΑΒ).
Αλλά στο βιβλίο αυτό, για απλούστευση, θα γράφουμε απλά: μήκος
ΑΒ.
|
|
| Συχνά ακούμε την φράση:
«Βρισκόμαστε στο μέσο της διαδρομής» και καταλαβαίνουμε ότι απέχουμε
την ίδια απόσταση από τα δύο άκρα. Τι ονομάζουμε λοιπόν μέσο του
ευθυγράμμου τμήματος; |
 |
- Μέσο ενός ευθύγραμμου τμήματος ΑΒ ονομάζουμε το σημείο Μ του τμήματος, που απέχει εξίσου από τα άκρα του.
|
|
|
|
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
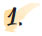 |
| Να σχεδιαστεί το ευθύγραμμο τμήμα ΓΔ, το
οποίο είναι ίσο με το τμήμα ΑΒ: (α) με το υποδεκάμετρο και (β) με
διαβήτη. |
 |
|
 |
|
| |
|
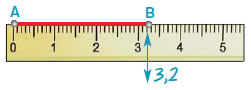
(α) |
Με το υποδεκάμετρο μετράμε το ευθύγραμμο
τμήμα ΑΒ και βρίσκουμε ότι ΑΒ = 3,2 cm.
Στη συνέχεια πάνω σε μια ευθεία ε παίρνουμε ένα
ευθύγραμμο τμήμα ΓΔ με μήκος ίσο με 3,2 cm,
όπως δείχνει το σχήμα. |
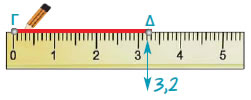 |
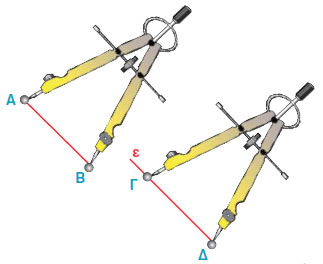
(β) |
Ανοίγουμε το διαβήτη, ώστε η μία άκρη του να
ακουμπάει στο Α και η άλλη στο Β.
Μετακινούμε το διαβήτη, χωρίς να
μεταβάλλουμε το άνοιγμα του. |
 |
Χαράζουμε μια ευθεία ε.
Τοποθετούμε τη μία άκρη του διαβήτη σε ένα
σημείο Γ της ε και με το άλλο άκρο,
που έχει τη γραφίδα, βρίσκουμε το σημείο Δ της ε.
Τότε το ευθύγραμμο τμήμα ΓΔ είναι ίσο με το ΑΒ. |
|
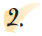 |
Να βρεθούν κατάλληλοι τρόποι σύγκρισης δύο
ευθύγραμμων τμημάτων και να διατυπωθούν τα συμπεράσματα. |
| |
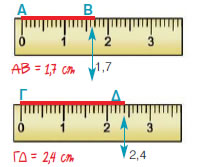
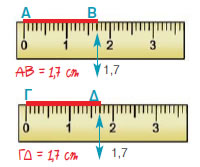
Ο 1ος τρόπος είναι να κάνουμε τη
μέτρηση με το υποδεκάμετρο.
| 1η περίπτωση |
2η περίπτωση |
3η περίπτωση |
 |
 |
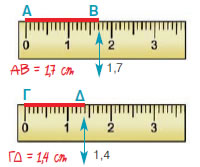 |
| ΑΒ < ΓΔ |
ΑΒ = ΓΔ |
ΑΒ > ΓΔ |
Ο 2ος τρόπος είναι να τα
συγκρίνουμε χρησιμοποιώντας το διαβήτη.
Ακουμπάμε τη μία άκρη του διαβήτη στο Α και την άλλη στο Β. Μετακινούμε το διαβήτη, χωρίς να
μεταβάλουμε το άνοιγμά του και τοποθετούμε το ένα άκρο του στο σημείο Γ και το άλλο επί της ημιευθείας ΓΔ. Ονομάζουμε Δ΄ το σημείο στο οποίο καταλήγει το δεύτερο άκρο του διαβήτη. Τότε έχουμε
τρεις περιπτώσεις.
| 1η περίπτωση |
2η περίπτωση |
3η περίπτωση |
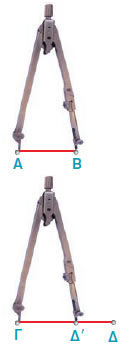
Το Δ΄ βρίσκεται ανάμεσα στα σημεία Γ και Δ. |

Το Δ΄ συμπίπτει με το Δ. |
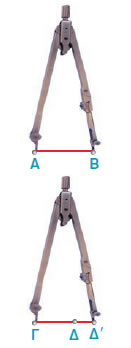
Το Δ΄ βρίσκεται στην προέκταση του ΓΔ προς
το Δ. |
| Τότε λέμε ότι το ΑΒ είναι μικρότερο από το ΓΔ και γράφουμε ΑΒ <
ΓΔ |
Τότε λέμε ότι τα ΑΒ και ΓΔ έχουν το ίδιο μήκος και γράφουμε ΑΒ = ΓΔ |
Τότε λέμε ότι το ΑΒ είναι μεγαλύτερο από το ΓΔ και γράφουμε ΑΒ >
ΓΔ |
|
 |
Να βρεθεί το μέσο ενός ευθύγραμμου τμήματος ΑΒ. |
 |
|
| |
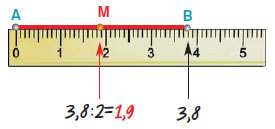
Με το υποδεκάμετρο βρίσκουμε ένα σημείο Μ
του ΑΒ, για το οποίο είναι:
ΑΜ = 3,8 : 2 = 1,9 cm.
Αλλά τότε και ΜΒ = 3,8 : 2 = 1,9 cm.
Δηλαδή: ΑΜ = ΜΒ. |
 |
|
|
| |
- Οποιοδήποτε
ευθύγραμμο τμήμα ΑΒ έχει πάντα ένα μέσο Μ, που είναι και μοναδικό.
|
|
|
Μικροπείραμα  Μικροπείραμα Μικροπείραμα |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
Συμπλήρωσε τα παρακάτω κενά:
(α) Το μήκος του ευθύγραμμου τμήματος ΑΒ,
που ενώνει δύο σημεία Α και Β λέγεται …………………….… των σημείων.
(β) Μέσο ενός ευθύγραμμου τμήματος ΑΒ
ονομάζουμε το σημείο του Μ που ……..…………... από τα άκρα του. |
 |
|
 |
Τοποθέτησε ένα "x" στη θέση που αντιστοιχεί στη
σωστή απάντηση: Από δύο σημεία μπορούν να περάσουν  Άπειρες
ευθείες, Άπειρες
ευθείες,  Μία
μόνο ευθεία, Μία
μόνο ευθεία,  Δύο μόνο ευθείες. Δύο μόνο ευθείες. |
 |
Ένα τόπι ύφασμα είναι 65 m. Πουλήθηκαν κομμάτια
με μήκη: 3,5 m, 25 cm, 7,95 m και 3,74 m. Πόσα μέτρα ύφασμα έμεινε στο
τόπι; |
 |
Το εμπορικό τρίγωνο μιας πόλης περικλείεται από
τις οδούς Ιπποκράτους, μήκους 619 m, Κλεισθένους, μήκους 271 m και
Περικλέους, μήκους 205 m. Πόσα βήματα θα κάνει ένας πεζός που κινείται
περιμετρικά στο εμπορικό τρίγωνο, αν το κάθε του βήμα είναι 75 cm. |
 |
Ένας αγρότης θέλει να περιφράξει έναν αγρό
σχήματος τετραγώνου και πλευράς 15,3 m. Διαθέτει συρματόπλεγμα, μήκους
60 m 3 dm 18 cm. Να βρεθεί, αν θα του φτάσει το συρματόπλεγμα ή αν
πρέπει να αγοράσει και άλλο.
Μικροπείραμα  |
 |
Ο παρακάτω πίνακας δείχνει την ακτίνα σε m
και σε Κm τεσσάρων πλανητών. Να συμπληρωθούν τα κενά: |
| Ακτίνα |
σε m |
σε Κm |
| ΑΦΡΟΔΙΤΗ |
6.085.000 |
|
| ΓΗ |
|
6.378 |
| ΑΡΗΣ |
|
3.750 |
| ΔΙΑΣ |
71.400.000 |
|
|
|
 |
| Οι
αριθμοί που εμφανίζονται στον παρακάτω πίνακα είναι τα μήκη των πέντε
πλευρών του πολυγώνου ΑΒΓΔΕ, εκφρασμένα με διαφορετικές μονάδες. Να
συμπληρωθεί ο πίνακας και να υπολογιστεί η περίμετρος του πολυγώνου σε
cm, dm και m. |
| |
ΑΒ |
ΒΓ |
ΓΔ |
ΔΕ |
ΕΑ |
Περίμετρος |
| cm |
517 |
|
|
1250 |
|
|
| dm |
|
|
|
|
7,6 |
|
| m |
|
4,2 |
0,84 |
|
|
|
|
|
 |
Πάρε ένα σημείο Α. Να βρεις τρία σημεία που το
καθένα να απέχει 2,7 cm από το Α. |
 |
Σχεδίασε δύο αντικείμενες ημιευθείες Αx και Αx΄.
Να βρεις πάνω στην ημιευθεία Αχ δύο σημεία Β και Γ, έτσι ώστε ΑΒ = 3 cm
και ΑΓ = 3,8 cm. Επίσης στην ημιευθεία Αx΄ να πάρεις ένα σημείο Δ έτσι,
ώστε ΑΔ = 3 cm. Να συγκρίνεις (α) τα ευθύγραμμα τμήματα ΑΓ και ΑΔ και
(β) τα ευθύγραμμα τμήματα ΑΒ και ΑΔ. |
 |
Σε μία ευθεία ε, πάρε στη σειρά τα σημεία Α, Β, Γ
και Δ έτσι ώστε να είναι: ΑΒ = 2,5 cm, ΒΓ = 3 cm και ΓΔ = 2,5 cm.
Εξέτασε αν τα τμήματα ΑΓ και ΒΔ είναι ίσα. |
 |
Το μέσο Ο ευθύγραμμου τμήματος ΑΒ απέχει 4,2 cm
από το άκρο Α. Πόσο είναι το μήκος του ΑΒ; |
 |
Σχεδίασε ένα ευθύγραμμο τμήμα ΑΒ. Να βρεις ένα
σημείο Μ, το οποίο να απέχει 3,3 cm από το Α και να μη βρίσκεται στην
ευθεία ΑΒ. Να φέρεις την ευθεία, η οποία περνάει από το Μ και από το
μέσο του ευθύγραμμου τμήματος ΑΒ. |
|
|