Β.1.13. Θέσεις ευθείας και κύκλου

Μέρος Β' - Κεφάλαιο 1ο - Βασικές γεωμετικές έννοιες

Ας εξετάσουμε τώρα τις σχετικές θέσεις που μπορεί να έχουν σ' ένα επίπεδο ένας κύκλος και μια ευθεία;

Θυμόμαστε - Μαθαίνουμε

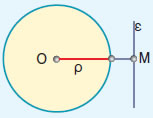
	Όταν ευθεία και κύκλος δεν έχουν κανένα κοινό σημείο λέμε ότι η ευθεία είναι εξωτερική του κύκλου. Όταν η απόσταση ΟΜ του κέντρου Ο από την ευθεία ε είναι μεγαλύτερη από την ακτίνα ρ (ΟΜ > ρ), η ευθεία είναι εξωτερική του κύκλου.
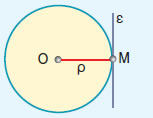
	Όταν ευθεία και κύκλος έχουν ένα μόνο κοινό σημείο Μ, η ευθεία λέγεται εφαπτόμενη του κύκλου στο σημείο Μ. Όταν η απόσταση ΟΜ του κέντρου Ο από την ευθεία ε είναι ίση με την ακτίνα ρ (ΟΜ = ρ), η ευθεία είναι εφαπτομένη του κύκλου στο Μ.
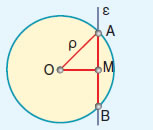
	Όταν ευθεία και κύκλος έχουν δύο κοινά σημεία Α και Β, η ευθεία λέγεται τέμνουσα του κύκλου ή λέμε ότι η ευθεία τέμνει τον κύκλο στα Α και Β Όταν η απόσταση ΟΜ του κέντρου Ο από την ευθεία ε είναι μικρότερη από την ακτίνα ρ (ΟΜ < ρ), η ευθεία είναι τέμνουσα του κύκλου.

Μικροπείραμα

ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ

Εικόνα

Να σχεδιαστεί κύκλος που να εφάπτεται σε σημείο μιας ευθείας.

Εικόνα

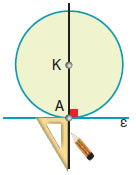Παίρνουμε μια ευθεία ε και το σημείο της Α. Σχεδιάζουμε την ευθεία που είναι κάθετη στην ε στο σημείο Α. Με κέντρο ένα οποιοδήποτε σημείο Κ της κάθετης αυτής και ακτίνα το τμήμα ΚΑ γράφου- με κύκλο. Ο κύκλος που φέραμε θα εφάπτεται στην ευθεία ε, διότι αυτή είναι κάθετη στην ακτίνα ΚΑ του κύκλου στο άκρο της Α.

Εικόνα

Να σχεδιαστεί ευθεία που να εφάπτεται σε σημείο ενός κύκλου.

Εικόνα


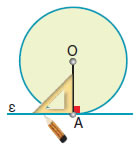Παίρνουμε ένα κύκλο (Ο, ρ) και το σημείο του Α. Σχεδιάζουμε την ευθεία ε, που είναι κάθετη στην ακτίνα ΟΑ στο σημείο Α. Η ευθεία ε θα εφάπτεται στον κύκλο στο σημείο Α, διότι είναι κάθετη στην ακτίνα ΟΑ στο άκρο της Α.

Να σχεδιαστούν εφαπτόμενες ενός κύκλου (Ο, ρ) στα άκρα Α και Β μιας χορδής του ΑΒ.

Εικόνα

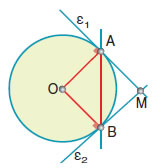Σχεδιάζουμε τις ακτίνες ΟΑ και ΟΒ. Στο σημείο Α της ακτίνας ΟΑ φέρνουμε την ευθεία ε₁ κάθετη στην ακτίνα αυτή. Η ευθεία ε₁ είναι εφαπτομένη του κύκλου στο σημείο Α. Στο σημείο Β της ακτίνας ΟΒ φέρνουμε την ευθεία ε₂ κάθετη στην ακτίνα αυτή. Η ευθεία ε₂ είναι εφαπτομένη του κύκλου στο σημείο Β.

Αν είναι Μ το σημείο που τέμνονται οι εφαπτόμενες, τα ευθύγραμμα τμήματα ΑΜ και ΒΜ λέγονται εφαπτόμενα τμήματα του κύκλου

Μικροπείραμα Μικροπείραμα Μικροπείραμα

ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ

	Να σχεδιάσεις δύο παράλληλες ευθείες ε₁ και ε₂ που να απέχουν μεταξύ τους 2,5 cm. Να πάρεις ένα σημείο Μ της ε₁ και να βρεις σημεία της ε₂. που απέχουν 3,6 cm από το Μ.
	Να σχεδιάσεις ένα ευθύγραμμο τμήμα ΑΒ = 3,6 cm και έναν κύκλο με διάμετρο την ΑΒ. Να χαράξεις τις εφαπτόμενες του κύκλου που διέρχονται από τα Α και Β. Να δικαιολογήσεις γιατί οι εφαπτόμενες αυτές είναι ευθείες παράλληλες.
	Παίρνουμε έναν κύκλο (Ο, ρ) και μια ευθεία ε. Ονομάζουμε δ την απόσταση του κέντρου Ο από την ευθεία ε. Να βρεις τον αριθμό των κοινών σημείων του κύκλου και της ευθείας, στις περιπτώσεις: (α) Αν ρ = 5 cm και δ = 4 cm, (β) αν ρ = 2,5 cm και δ = 2,5 cm και (γ) αν ρ = 3 cm και δ = 6 cm.
	Να σχεδιάσεις δύο κάθετες ευθείες ε₁ και ε₂ και να ονομάσεις Α το σημείο τομής τους. Να πάρεις ένα σημείο Κ της ε₁ ώστε να είναι ΚΑ = 3,1 cm. Να φέρεις τους κύκλους (Κ, 2,1cm), (Κ, 3,1cm) και (Κ, 36 cm). Να βρεις ποια είναι η θέση της ε₂ ως προς τους κύκλους αυτούς.
	Να σχεδιάσεις ένα ευθύγραμμο τμήμα ΑΒ = 40 mm. Να πάρεις ένα σημείο Μ του ΑΒ, ώστε να είναι ΑΜ = 18 mm. Να φέρεις τους κύκλους (Α, 18 mm) και (Β, 22 mm). Να χαράξεις ευθεία ε που να διέρχεται από το Μ και να είναι κάθετη στην ΑΒ. Ποια είναι η θέση της ε ως προς τον καθένα από τους κύκλους; Να δικαιολογήσεις την απάντησή σου.

ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΠΑ ΤΟ ΣΠΙΤΙ

Εικόνα

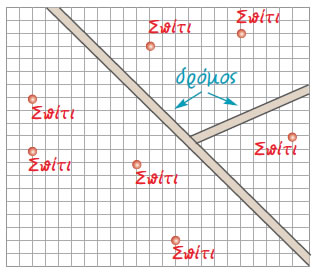
Μια επιχείρηση αποφάσισε να κατασκευάσει ένα εργοστάσιο σε μια αγροτική περιοχή που επιλέγει για το σκοπό αυτό. Η πλευρά κάθε τετραγώνου του σχήματος της επόμενης σελίδας, αντιπροσωπεύει απόσταση 100 m. Το εργοστάσιο πρέπει να βρίσκεται τουλάχιστον σε ακτίνα 600 m μακριά από τα σπίτια (Σ). Επίσης πρέπει να απέχει το λιγότερο 300 m από την άκρη του δρόμου. Να αντιγράψεις σε τετραγωνισμένο χαρτί το σχήμα και να χρωματίσεις τις περιοχές όπου μπορεί να κατασκευαστεί το εργοστάσιο.

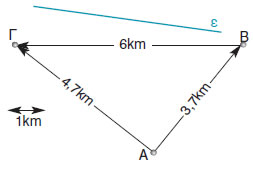
Η συμφωνία μεταξύ των χωριών Α, Β και Γ για την κατασκευή μιας γεώτρησης σε μια θέση Μ περιλαμβάνει τους εξής τρεις όρους:

α) ΑΜ > 2 km, β) ΒΜ = 3 km και γ) ΓΜ = 4 km. Να αντιγράψεις το παρακάτω σχήμα και να βρεις τη θέση του σημείου Μ, καθώς και την απόσταση της θέσης αυτής από το δρόμο ε.