| Β.1.11. Κύκλος και στοιχεία του κύκλου |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η |
 |
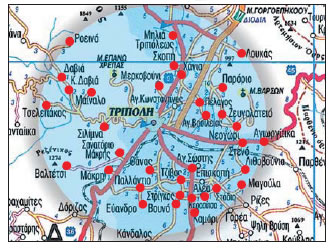
| Στην Τρίπολη της Αρκαδίας γίνεται μια
γιορτή, στην οποία είναι καλεσμένοι οι κάτοικοι, που κατοικούν σε
απόσταση μικρότερη των 6 Κm. Ποιων χωριών οι κάτοικοι θα παρευρεθούν
στη γιορτή; |
 |
|
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η |
| |
 |
Ο πρωτόγονος άνθρωπος για να μη χάσει την
κατσίκα του την έδεσε με ένα σχοινί, σ' ένα ξύλινο πάσσαλο, μέσα στο
λιβάδι.
Όταν γύρισε να την πάρει είδε ότι η κατσίκα
είχε βοσκήσει εκείνο το μέρος του λιβαδιού που της επέτρεπε το μήκος
του σχοινιού να φθάσει. Έτσι, όλα τα χόρτα που απείχαν μικρότερη ή ίση
απόσταση από το σχοινί, που ήταν δεμένη, είχαν φαγωθεί. |
- Ποια γεωμετρική έννοια
χαρακτηρίζει την περιοχή της οποίας το χορτάρι φαγώθηκε;
|
Μικροπείραμα  |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η |
| |
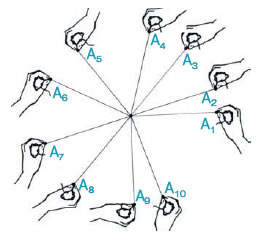
Να βρεθούν δέκα διαφορετικά σημεία, που ν' απέχουν
όλα 2 cm από ένα σημείο Α.
Με τη βοήθεια ενός υποδεκάμετρου μετράμε και
βρίσκουμε το ακριβές μήκος των 2 cm σε ένα σχοινί.
Μετά, κρατώντας με το ένα χέρι τη μία άκρη
αυτού του σχοινιού στο σημείο Α και έχοντας πάντα τεντωμένο το σχοινί,
κινούμε με το άλλο χέρι την άλλη άκρη του μήκους αυτού, των 2 cm, σε
δέκα διαφορετικές θέσεις Α1, Α2, Α3, Α4,
Α5, Α6, Α7, Α8, Α9 και Α10, που επιλέγουμε στην τύχη, βρίσκοντας τα αντίστοιχα
δέκα ζητούμενα διαφορετικά σημεία.
Βλέπουμε ότι τα σημεία, που απέχουν μια
συγκεκριμένη απόσταση από σταθερό σημείο, είναι πάρα πολλά. |
|
- Τι σχήμα φτιάχνουν,
λοιπόν, όλα αυτά τα σημεία με την κοινή αυτή ιδιότητα;
|
|
| |
 |
Μέσα από την καθημερινή ζωή μπορούμε να βρούμε
αρκετά παραδείγματα καμπυλών. Όπως π.χ. ο ήλιος στη δύση του, ο τροχός
ενός ποδηλάτου η στεφάνη της μπασκέτας, ένα μεταλλικό νόμισμα, το ρολόι
μας, μια τούρτα γενεθλίων, ένας δίσκος μουσικής κλ.π |
 |
| Το πρώτο σχήμα που
μπορούσε να επινοήσει ή να ανακαλύψει στη γη ο άνθρωπος είναι φυσικά, ο
κύκλος. Ο ήλιος και το φεγγάρι αρκούν για να δώσουν στο μάτι το σχήμα
και στην ψυχή την ομορφιά της τελειότητας. Και όταν φθάσει η ώρα της
σκέψης, τότε η Γεωμετρία αποκτά το πιο πολύτιμο σχήμα της. |
|
| |
|
 |
- Κύκλος λέγεται
το σύνολο όλων των σημείων του επιπέδου που απέχουν την ίδια απόσταση
από ένα σταθερό σημείο Ο.
- Η απόσταση
αυτή συμβολίζεται με ρ και λέγεται ακτίνα του κύκλου. Το σημείο Ο
λέγεται κέντρο του κύκλου.
- Ένας κύκλος με
κέντρο Ο και ακτίνα ρ, συμβολίζεται
με συντομία (Ο, ρ).
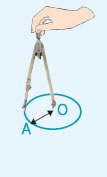
- Για να σχεδιάσουμε
ένα κύκλο χρησιμοποιούμε το διαβήτη.
- Δύο κύκλοι με
ακτίνες ίσες είναι ίσοι.
|
 |
Επίσης:
- Το ευθύγραμμο
τμήμα ΑΒ, που συνδέει δύο σημεία Α και Β του κύκλου, λέγεται χορδή του κύκλου.
|
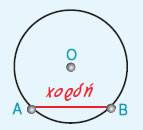 |
- Ειδικά η χορδή που περνάει από το κέντρο του κύκλου λέγεται διάμετρος του κύκλου.
- Η διάμετρος είναι η μεγαλύτερη χορδή του κύκλου, είναι διπλάσια από την ακτίνα του
κύκλου και χωρίζει τον κύκλο σε δύο ίσα μέρη (ημικύκλια).
|
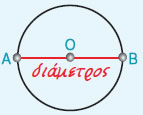 |
- Δύο σημεία Α και Β του κύκλου τον χωρίζουν σε δύο μέρη που το
καθένα λέγεται τόξο του κύκλου με άκρα τα Α και Β.
|
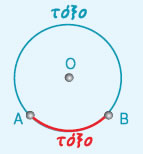 |
- Κυκλικός
δίσκος (Ο, ρ) είναι ο κύκλος (Ο, ρ) μαζί με το μέρος του επιπέδου που
περικλείει.
- Όλα τα
σημεία του κυκλικού δίσκου απέχουν από το κέντρο Ο απόσταση μικρότερη ή
ίση με την ακτίνα ρ.
|
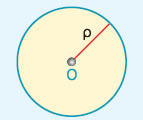 |
Μικροπείραμα  Μικροπείραμα Μικροπείραμα  |
| |
| ΠΑΡΑΔΕΙΓΜΑ - ΕΦΑΡΜΟΓΗ |
| |
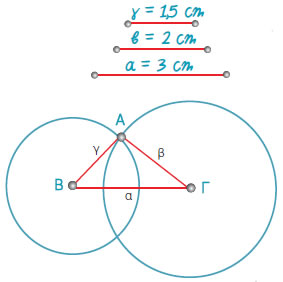
Να σχεδιαστεί ένα τρίγωνο, αν γνωρίζουμε τα μήκη
των πλευρών του. |
|
 |
 |
|
 |
| |
Ας υποθέσουμε ότι τα ευθύγραμμα τμήματα α
= 3 cm, β = 2 cm και γ = 1,5 cm είναι οι
πλευρές του τριγώνου που πρέπει να σχεδιάσουμε. Ακολουθούμε την εξής
διαδικασία: Παίρνουμε ένα από αυτά και το ονομάζουμε πλευρά ΒΓ
= α.
Μετά χαράζουμε τους κύκλους (Β,γ = 1,5 cm) και (Γ,β = 2 cm). Οι δύο αυτοί κύκλοι τέμνονται στο
σημείο Α. Το τρίγωνο ΑΒΓ είναι το
ζητούμενο διότι έχει πλευρές: ΒΓ = 3 cm, ΑΒ = 1,5 cm,
ως ακτίνα του κύκλου (Β,1,5 cm) και ΑΓ = 2
cm, ως ακτίνα του κύκλου (Γ,2 cm), αφού το Α
ανήκει και στους δύο κύκλους. |
Μικροπείραμα  |
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
 |
Με κέντρο ένα σημείο Μ να σχεδιάσεις κύκλους με
ακτίνες 2,4 cm, 2 cm και 15 mm. |
 |
 |
Να σχεδιάσεις τον κύκλο που έχει διάμετρο ένα
ευθύγραμμο τμήμα ΑΒ = 3,8 cm. |
 |
Να σχεδιάσεις ομόκεντρους κύκλους με κέντρο
σημείο Μ και διαμέτρους 4 cm, 5 cm και 48 mm. (Δύο κύκλοι λέγονται
ομόκεντροι, αν έχουν το ίδιο κέντρο και διαφορετικές ακτίνες) |
 |
Να σχεδιάσεις έναν κύκλο με κέντρο σημείο Κ και
ακτίνα 3,4 cm. Να πάρεις ένα σημείο Μ του κύκλου αυτού και να χαράξεις
δύο χορδές του: ΜΑ = 2,4 cm και ΜΒ = 4,1 cm. |
 |
Έστω ευθύγραμμο τμήμα ΑΒ = 4 cm. (α) Να βρεις τα
σημεία του επιπέδου που απέχουν: 3 cm από το Α και 2 cm από το Β. (β)
Ποια σημεία απέχουν ταυτόχρονα 3 cm από το Α και 2 cm από το Β; |
 |
Έστω ευθύγραμμο τμήμα ΑΒ = 3,2 cm. Να σχεδιάσεις
τους κύκλους (Α, ΑΒ) και (Β, ΑΒ) και να ονομάσεις Μ και Ν τα σημεία στα
οποία τέμνονται οι κύκλοι αυτοί Να βρεις τις αποστάσεις του Μ από τα
άκρα Α και Β καθώς και τις αποστάσεις του Ν από τα Α και Β. Στη
συνέχεια να συγκρίνεις τις αποστάσεις αυτές. |
|
Μικροπείραμα 
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΠΑ ΤΟ ΣΠΙΤΙ |
|
|