| Α.7.9. Δυνάμεις ρητών αριθμών με εκθέτη ακέραιο |
| |
|
Σύμφωνα με τον κανόνα της διαίρεσης των δυνάμεων με την ίδια βάση, που μάθαμε στην προηγούμενη παράγραφο, είναι:
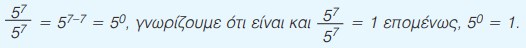
Με την έννοια αυτή ορίζουμε: |
 |
- Η δύναμη κάθε αριθμού, διάφορου του μηδενός με εκθέτη το μηδέν είναι ίση με μονάδα.
|
|
Επίσης, θα είναι:
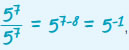 γνωρίζουμε ότι είναι και γνωρίζουμε ότι είναι και  , άρα , άρα 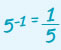
|
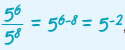 γνωρίζουμε ότι είναι και γνωρίζουμε ότι είναι και  , άρα , άρα 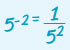
κ.ο.κ. Με την έννοια αυτή ορίζουμε: |
|
|
|
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
 |
Να υπολογιστούν οι δυνάμεις: (α) (-2)-5, (β) -3-3, (γ) (-234567)0. |
 |
 |
|
 |
Να υπολογιστούν οι τιμές των παραστάσεων: 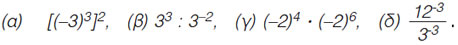 |
 |
|
| |
| (α) |
[(-3)3]2 = (-3)3·2 = (-3)6 = 729 |
| (β) |
33 : 3-2 = 33-(-2) = 33+2 = 35 = 243 |
| (γ) |
(-2)4 · (-2)6 = (-2)4+6 = (-2)10 = 1024 |
| (δ) |
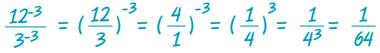 |
|
|
 |
Να υπολογιστούν οι δυνάμεις: 10-1, 10-2, 10-3, 10-4, 10-5, 10-6, 10-7. |
|
 |
|
|
| |
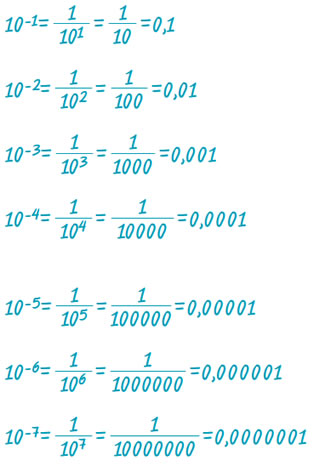 |
|
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
|